交换半环上广义矩阵代数的Jordan导子

庄金洪， 陈艳平， 谭宜家

(1. 福建商学院信息工程学院, 福建 福州 350012; 2. 福州大学数学与计算机科学学院, 福建 福州 350108)

0 引言

关于Jordan导子已有很多研究. 1957年， 文献[1]证明了特征不等于2的素环上每个Jordan导子都是导子， 该结果被推广到不同的环和代数上[2- 5]. 文献[4]证明了三角代数上 每一个Jordan导子是导子. 近年来， 人们致力于将三角代数的线性映射理论发展到广义矩阵代数的情形[6-8]. 广义矩阵代数的线性映射研究主要是在交换环的基础上进行讨论的， 但对于交换半环上广义矩阵代数的线性映射研究比较少. 因此, 本研究将探讨交换半环上广义矩阵代数的Jordan导子、 导子与反导子.

1 预备知识

定义1[9]设R是一非空集合, “+”与”·”是定义在R中的两个代数运算. 如果以下条件成立：

1) (R, +, 0)是一个交换幺半群， 其中0为R的加法恒等元；

2) (R, ·, 1)是一个幺半群， 其中1为R的乘法恒等元；

3) 对任意的a,b,c∈R, 均有a(b+c)=ab+ac, (a+b)c=ac+bc；

4) ∀a∈R, 0a=a0=0；

5) 0≠1.

则称R为一个半环， 记为(R, +, ·, 0, 1)或简记为R. 这里， 加法恒等元0称为半环R的零元， 乘法恒等元1称为R的单位元.

如果∀a,b∈R, 均有ab=ba, 则称半环R是交换的. 如果∀a,b∈R, 由a+c=b+c可推岀a=b,则称c是加法可消的. 如果R的所有元素都是加法可消的， 那么称半环R是加法可消的. 对于a∈R, 如果存在b∈R, 使得:a+b=0, 则称a是R中的可反元， 并记b=-a， 这时， ∀c∈R, 定义c-a=c+(-a).

定义2[9]设R为半环， (M, +, 0)为交换幺半群， 若存在从R×M到M的一个映射(r,m)|→rm， 满足下列五个条件， 即对于任意r,r′∈R,m,m′∈M， 均有:

Ⅰ)r(m+m′)=rm+rm′; Ⅱ) (r+r′)m=rm+r′m;

Ⅲ) (rr′)m=r(r′m); Ⅳ) 1Rm=m; Ⅴ)r0=0=0m.

则称M为半环R上的一个左半模， 简称左R-半模.

一个左R-半模M称为忠实的, 如果∀r,r′∈R, 当对于所有m∈M, 均有rm=r′m时,r=r′. 类似地， 可定义半环R上的右半模和忠实右半模.

设R和S是半环， (M, +, 0)是一个交换幺半群. 称(M, +, 0)是一个(R,S)-双半模， 如果M既是左R-半模， 又是右S-半模， 且∀r∈R,m∈M,s∈S, 均有: (rm)s=r(ms)成立.

定义3[9]设R是一个交换半环, (A, +, ·, 0, 1)是一个半环. 如果(A, +, 0)是R上的一个左半模, 且∀r∈R,x,y∈A, 均有：r(xy)=(rx)y=x(ry)成立, 则称A是R上的一个代数.

定义4设A,B是半环R上的一个代数，M，N是(A,B)-双半模，η:M→N是一个映射. 如果∀x,y∈M,a∈A，b∈B,η(x+y)=η(x)+η(y),η(ax)=aη(x)，η(xb)=η(x)b, 则称η为M到N的(A,B)-双半模同态.

定义5[10]设B是交换半环R上的代数，MB是右B-半模，BN是左B-半模，M×N是集合M,N的卡氏积， (V, +, 0)是一个交换幺半群. 映射f:M×N→V称为B-平衡的， 如果∀m,m′∈M,n,n′∈N,b∈B, 均有:

ⅰ)f(m+m′,n)=f(m,n)+f(m′,n)； ⅱ)f(m,n+n′)=f(m,n)+f(m,n′)；

ⅲ)f(mb,n)=f(m,bn)； ⅳ)f(m, 0)=0=f(0,n).

定义6[10]设B是交换半环R上的代数，MB是右B-半模，BN是左B-半模， (V, +, 0)是交换幺半群,f:M×N→V是B-平衡映射. 二元组(V,f)称为MB和BN张量积， 如果对任意给定的交换幺半群(W, +, 0)和任意的B-平衡映射α:M×N→W， 存在唯一的半群同态β:V→W， 使得α=β∘f， 记V=M⊗BN，f(m,n)=m⊗n.

命题1[10]设(M⊗BN, ⊗)是半模MB和BN的张量积, 那么∀m,m′∈M,n,n′∈N,b∈B, 均有:

② (m+m′)⊗n=m⊗n+m′⊗n,m⊗(n+n′)=m⊗n+m⊗n′；

③ (mb)⊗n=m⊗(bn)；

④m⊗0=0=0⊗n.

设A,B是交换半环R上的代数，AMB,BNA均是双半模， ∀m∈M,n∈N,a,b∈A, 定义a(m⊗n)=(am)⊗n, (m⊗n)b=m⊗(nb), 则由文献[10]知， 张量积M⊗BN是(A,A)-双半模； 类似地， 张量积N⊗AM是(B,B)-双半模.

定义8设A是R上的一个代数，d:A→A是一个R-线性映射. ∀a,b∈A, 如果d(ab)=d(a)b+ad(b), 则称d为A的一个导子； 如果d(ab)=d(b)a+bd(a), 则称d是一个反导子； 如果d(ab+ba)=d(a)b+ad(b)+d(b)a+bd(a), 则称d是一个Jordan导子. 如果存在可反元g∈A, 使得d(a)=ag-ga=ag+(-g)a， 则可验证d是A的一个导子， 称d为由g诱导的内导子， 记为dg.

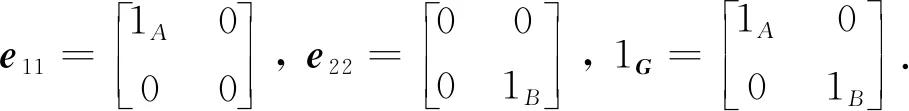
2 主要结果及其证明

引理1[11]设R是一个交换半环,A是R上的一个代数，Δ:A→A是A上的一个Jordan导子. 那么∀a∈A, 均有Δ(a2)=Δ(a)a+aΔ(a).

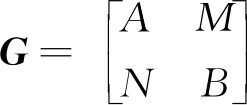
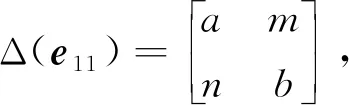
Δ-dg2=Δ2， 唯一性得证.

由引理2知， 想要获得广义矩阵代数G的Jordan导子的结构， 只需给岀广义矩阵代数G上满足Δ(e11)=0的Jordan导子Δ的结构即可.

(1)

其中：δA:A→A，μB:B→B分别是A和B上的Jordan导子；τM:M→M，vN:N→N，τN:N→M，vM:M→N均为R-线性映射. 同时， ∀a∈A,b∈B,m,m′∈M,n,n′∈N， 以下7点均成立：

1)δA(mn)=τM(m)n+mvN(n),μB(nm)=vN(n)m+nτM(m)；

2)τM(am)=δA(a)m+aτM(m),vM(am)=vM(m)a；

3)τM(mb)=τM(m)b+mμB(b),vM(mb)=bvM(m)；

4)vN(bn)=μB(b)n+bvN(n),τN(bn)=τN(n)b；

5)vN(na)=vN(n)a+nδA(a),τN(na)=aτN(n)；

6)mvM(m)=τN(n)n=0,vM(m)m=nτN(n)=0；

证明 充分性可以通过直接验算证明， 下证必要性.

由于Δ:G→G是一个Jordan导子， 故∀X,Y∈G, 有：

Δ(XY+YX)=Δ(X)Y+XΔ(Y)+Δ(Y)X+YΔ(X)

(2)

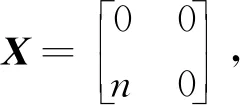
(3)

其中：δA:A→A和μB:B→B分别是A与B上的导子；τM:M→M和vN:N→N均为R-线性映射. 同时， ∀a∈A,b∈B,m∈M,n∈N， 均有：

Ⅰ)δA(mn)=τM(m)n+mvN(n),μB(nm)=vN(n)m+nτM(m)；

Ⅱ)τM(am)=δA(a)m+aτM(m),τM(mb)=τM(m)b+mμB(b)；

Ⅲ)vN(bn)=μB(b)n+bvN(n),vN(na)=vN(n)a+nδA(a).

证明 通过直接验算可证充分性， 下证必要性.

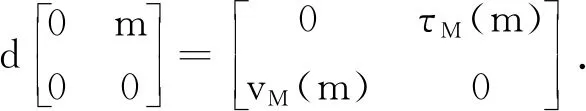
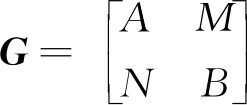
(4)

其中:τN:N→M，vM:M→N是R-线性映射. 同时∀a∈A,b∈B,m,m′∈M,n,n′∈N, 均存在：

ⅰ)vM(am)=vM(m)a，vM(mb)=bvM(m),τN(na)=aτN(n),τN(bn)=τN(n)b;

ⅱ)mvM(m′)=τN(n)n′=0,vM(m)m′=nτN(n′)=0.

证明 通过直接计算可得h是G的反导子, 故充分性得证， 下证必要性.

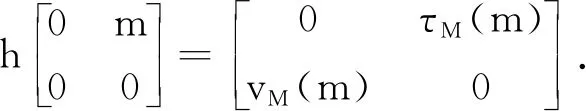
因为h是G的一个反导子， 所以∀X,Y∈G, 下式成立：

h(XY)=h(Y)X+Yh(X)

(5)

类似可证， 当N是忠实的(B,A)-双半模时， 结论也成立. 证毕.

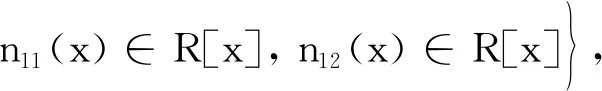
由于τM:M→M，vN:N→N，τN:N→M，vM:M→N均为R-线性映射且满足定理1中的1)～7). 所以这些映射满足定理2中的Ⅰ)～Ⅲ)和定理3中的ⅰ).

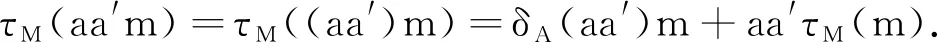
又由已知条件可得： ∀m,m′∈M,n,n′∈N，mvM(m′)=τN(n)n′=0,vM(m)m′=nτN(n′)=0. 再由定理3知，h是G的反导子.

类似可证， 当N是忠实的(B,A)-双半模时， 结论也成立. 下证唯一性.