例谈高中物理力学解题中整体法的运用

【摘 要】在“热”“光”“电”“力”“原”这高中物理五大知识板块中，“力”在每年的高考理综试卷中都占有很高的分数比重，因此掌握力学试题的解题方法对提升学生的高考成绩有很大的帮助。但力学部分知识点琐碎又难以理解，在具体分析物理问题时又很难正确运用，所以一些学生对这一部分知识非常头疼。其实力学问题是有规律的，只要选择恰当的思路，就能在解题时熟练地运用所学知识点。整体法作为力学中最常用的解题方法，在很多题型中都适用，因此教师要引导学生形成整体思维，这样学生在解题时才能够得心应手。本文主要介绍整体法，并探究整体法在高中物理力学解题中的运用策略。

【关键词】高中物理;力学;解题;整体法

【中图分类号】G633.7  【文献标识码】A  【文章编号】1671-8437（2021）34-0140-02

高考物理往往通過复杂的力学题考查学生是否具有严谨的思维、是否具有整体观念、是否具有分析能力。在大部分高考物理力学试题中，物体受到的力是复杂的，如果对物体的受力情况逐一分析，一方面不必要的力学分析会干扰学生解题，另一方面逐一分析受力情况非常费时间，这势必会影响学生的解题效率。整体法提倡在做题时抓大放小，关注主要研究对象，把它们当成一个系统而忽略系统内复杂的力学关系。运用整体法进行受力分析，学生解题的效率、准确率不仅能得到提高，也能使学生从整体角度对试题有清晰的认识，拓宽学生的解题思路。

1   整体法概述

在物理力学解题中，整体法就是先把主要研究对象当做一个整体，然后分析整体以外的物体对这个整体的作用力，而不需要分析这个整体内部的复杂的相互作用力[1]。当面对一个复杂的物理力学问题时，通过整体法的运用可以使分析过程化繁为简，学生掌握了整体法，复杂受力分析对于他们来说会变得更清晰、更有逻辑，面对力学试题也能摆脱无从下手的窘境，就能更快、更准确地解题。

2   力学解题中整体法运用的意义

2.1  提高解题效率

在高中物理力学教学中，受力分析往往令很多学生感到困惑，学生对于应该分析哪些物体的力、物体会受到哪些力没有清晰的认识。学生常常会因为没有更好的解题思路而去逐一分析每个物体的受力情况，这样会出现很多干扰性分析，而且分析时容易出现遗漏。如在遇到关于连接体的问题时，采用整体法将连接体当做一个整体去做力学分析，标明整体所受的各种外力，这样就简化了解题步骤，解题思路也会更清晰，自然就能起到提高解题效率的作用。

2.2  提高解题准确率

繁琐的解题过程容易使学生忽略细节，从而导致解题出错。运用整体法将整个解题步骤简化后，学生更能专注于解题目标与细节，也能有规律地、有逻辑性地解题，解题的准确率会得到大幅提高[2]。

2.3  拓宽解题思路

在高中物理力学解题中，整体法能够帮助学生立足宏观角度，筛选解决信息，在独立解决问题的过程中加深对相关知识的理解。运用整体法的过程中，学生可以从整体视角对相关问题进行分析，并区分对象间的联系，从而形成综合的、全面的物理解题思维。

3   高中物理力学解题中整体法的运用

高中生往往不能恰当使用整体法解题，如学生会将隔离法与整体法混淆，分不清在哪种情况下应该使用整体法，哪种情况应该用隔离法。这是由于学生不了解整体法与隔离法的本质区别。隔离法与整理法的正确运用需要学生通过大量做题去掌握。

3.1  物体平衡问题中整体法的应用

处于平衡状态的物体的受力情况不仅是高中物理的重要内容，还是每年高考中出现频率较高的试题类型。物理平衡问题主要有两个类型，分别是单个物体的平衡问题和连接体的平衡问题[3]。

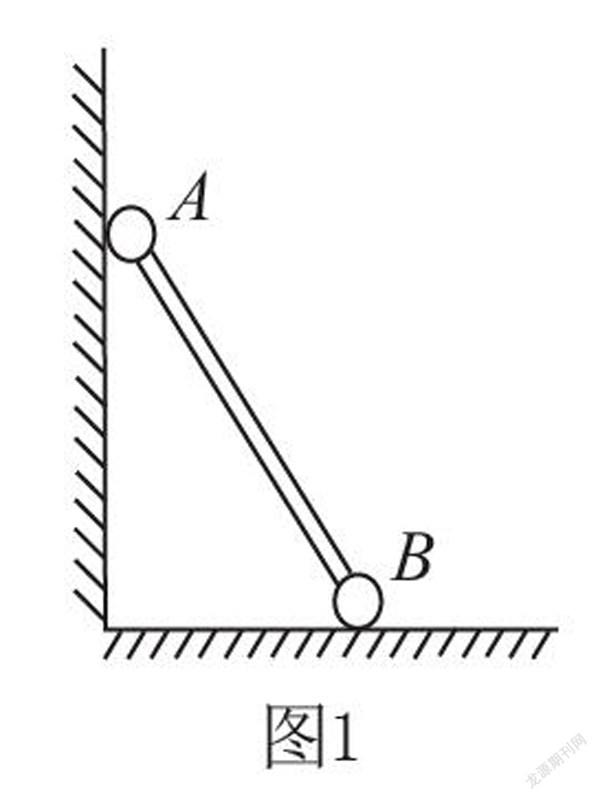
例1：现有用轻杆连接的两个质量都是m的小球A、B被斜放在墙上，此时处于平衡状态，如图1。A球抵在墙面上，B球置于地面。已知墙面是光滑的（可忽略作用力），水平地面粗糙。现在将A球向上移动，A、B两小球再次达到平衡状态，分析地面对B球的支持力和轻杆上的压力的变化情况。

解答这一题目需要同时用到整体法和隔离法。在题目中轻杆的质量一般忽略不计，在分析地面对B球的支持力时，就将A球、轻杆、B球当成一个整体，地面对B球的支持力始终等于这个整体的重力，所以平衡前和平衡后地面对B球的支持力都是2mg。找到题目中支持力的本质，运用整体法一步就能分析出目标的力学变化，而不用去分析整体内复杂的相互作用力。对于轻杆上的压力变化则可以使用隔离法单独对A球进行分析。

3.2  物体运动题目中整体法的运用

物体运动的题目主要有两种类型：单个物体多段运动、多个物体多段运动。在这类题目的解答中，对复杂运动情况的分析，是解决问题的关键。在下面的例题中笔者就用整体法来分析物体的多过程运动。

例2：有一质量为M=4 kg的木板静止在光滑水平面上（木板与地面间的摩擦力忽略），如图2，木板的右端放一质量为m=2 kg的小铜块，现给铜块一个水平向左的速度v=4 m/s，铜块在木板上滑行，与固定在木板左端的水平轻弹簧相碰后又返回，且恰好停在木板右端，求铜块与弹簧相碰过程中，弹性势能的最大值Ep。

在解此题目的过程中，运用整体法能够轻松找到守恒关系，从而列出等式，求出关键速度。木板置于光滑的水平面上，将铜块、木板、弹簧当做一个整体时，整个系统的动量是守恒的。因此弹簧压缩到最大时该系统的动量与铁块停在木板右端时相同，设分别为v、v，此时就可以列出等式（M+m）v=v（M+m）=mv0。求出v、v后根据机械能的损失，可以计算出弹性势能的最大值。因为铜块与木板之间存在相对运动，如果将铜块、木板、弹簧的运动状况分别分析，会因计算不出它们单独的速度和机械能转换，导致解题失败。但用整体法可以将这一系统相对于光滑的地面进行分析而列出等式，进而得出结果。

3.3  连接体试题中整体法的运用

连接体问题中往往研究对象较多、相互作用力也较多。在复杂的连接体问题中运用整体法，能减少研究对象，进行有针对性的分析。不计物体间的相互作用力或对象处于同一运动状态时可以运用整体法，对于大多数实际问题，还需要将整体法与隔离法结合使用，但选择研究对象时优先考虑整体，若不能解决再考虑运用隔离法[4]。

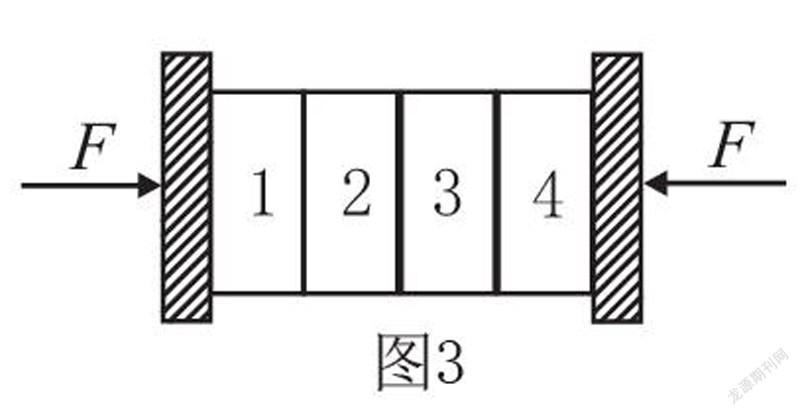
例3：两块相同木板竖直放置，它们中间有质量均为m的四块相同的砖，如图3，从左到右依次为1、2、3、4，用两个大小均为F的水平力压木板，使砖静止不动，则左边木板对第一块砖、第二块砖对第三块砖的摩擦力分别是多少？

本题中先将四块砖当做一个整体，设左、右木板对整体的摩擦力为 f，即左边木板对第一块砖的摩擦力，则可以列出等式2 f=4mg，得 f=2mg。在研究第二块砖对第三块砖的摩擦力时，设其摩擦力为 f，将1、2块砖当做一个整体，则可列等式 f+ f=2 mg，所以 f=0。

綜上所述，整体法的运用对于高中物理力学解题具有重要作用，学生掌握整体法非常有必要。首先选择恰当的研究对象作为一个系统，不先考虑系统内的相互作用力，先考虑系统外物体对系统的作用力，这样能对系统的整体情况有一个宏观的把握，然后再根据具体要求进行隔离分析。这样的解题步骤对大部分的物理力学试题均是适用的。从上面的例子可以看出，整体法的运用不仅能提高学生解题的准确率、效率，还能帮助学生实现综合思维力的发展。

【参考文献】

[1]任汉元.浅析高中物理力学解题中整体法的运用[J].数理化解题研究，2021（19）.

[2]陆文彬.浅议高中物理力学解题中整体法的运用[J].数理化解题研究，2021（9）.

[3]陈品.高中物理力学解题中整体法的运用探析[J].考试周刊，2021（26）.

[4]何强林.刍议高中物理力学解题方法的研究[J].华章，2013（8）.

【作者简介】

韩小军（1984～），男，汉族，甘肃陇西人，本科，中学高级教师。研究方向：高中物理。