基于数学史的“抛物线”教学

【摘 要】针对抛物线教学中的实际问题，从数学史实中寻找教学启示，给出使焦点、準线自然地出现的教学策略，在计算演绎的过程中推理证明二次函数的图象与标准方程下的抛物线同质，促进了学生理性思维的发展。

【关键词】抛物线的数学史;二次函数图象;抛物线教学

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2021）11-0013-04

【作者简介】李昌，南京师范大学灌云附属中学（江苏灌云，222200）教师，高级教师。

抛物线是中学数学的教学内容，其教学安排在初高中两个学段，高中学段的教学又分布于函数、几何与代数两条主线中，这种分散性使得一些学生认为作为二次函数图象的抛物线与解析几何标准方程的抛物线，二者名字虽相同但并非是相同的曲线。那么，高中阶段如何教学才能避免这种错误的认识？如何让抛物线解析定义中的焦点、准线自然呈现并与二次函数相关联？教学取向的数学史研究表明，教学中的这些问题都可以从数学史中找到答案或者启示。因此，教师要了解相关数学史料，选择合适方式融入教学;合理创设问题情境，通过计算演绎来推理证明二次函数图象是抛物线，促进学生形成正确的认知。以下是笔者的做法和思考，同大家交流。

一、抛物线数学史实简述

抛物线起源于圆锥截线，历史上的名称为“直角圆锥截线”“齐曲线”。柏拉图学派的梅奈克缪斯（Menaechmus）按圆锥顶角的大小将圆锥分为锐角、直角和钝角三类，用垂直于母线的平面截这些圆锥就得到“梅氏三线”，抛物线是其中的“直角圆锥截线”。阿波罗尼奥斯（Apollonius）发现在同一圆锥面中通过改变截面位置也能得到“梅氏三线”，其巨著《圆锥曲线论》代表了古希腊演绎几何的最高成就。他还将希腊几何学中的“应用”和欧几里得（Euclid）的“比例”相结合，通过推理得出椭圆、双曲线和抛物线的方程。

抛物线的焦点源于其光学性质，抛物面反射镜能将平行于轴的光线聚集到一点，“焦点”的概念由数学家狄俄克利斯（Diocles）在《取火镜》中提出，抛物线的几何性质以及轨迹定义是由古希腊几何学家喜帕普斯（Hipparchus）在《数学汇编》中给出。17世纪解析几何诞生，数学家用代数的方法重新研究圆锥曲线，法国数学家洛必达（lH?pital）推导了抛物线的标准方程。

数学家对抛物体运动轨迹的研究充满数学思维理性，经历了观察猜想、实验验证和理论推理的过程。14世纪，因对火炮射程的判断和控制需要研究斜抛运动的轨迹，起初人们认为轨迹由斜向上的直线段、圆弧、竖直向下的直线段组成。直到17世纪中期，伽利略（ Galilei）用实验的方法确定了平抛运动的轨迹不是直线而是类似于抛物线或双曲线抑或是悬链线，而后通过实际测量得出：在相等的时间间隔内，水平位移相等，而竖直位移与时间的平方成正比。从而通过实验得出平抛运动的轨迹就是阿波罗尼奥斯的齐曲线，理论上的证明则由数学家卡瓦列里（Cavalieri）完成。

依据认知发展的“历史相似性原理”可以预见，从抛物线的截线定义到解析定义是学生认知的难点;可以断定，初中教学时仅凭模糊的视觉认知来确认二次函数的图象是抛物线的做法符合认知发展规律，但不能满足高中阶段学生的思维发展需要，不能作为推理的起点。因此，高中阶段的教学应该思考如何揭示抛物线的焦点性质，如何才能使焦点准线自然呈现，怎样融合两种背景下抛物线数学本质的一致性，使学生形成正确的认知等问题，笔者的教学实践如下。

二、关于焦点、准线的教学

教科书和许多教师在建构抛物线解析定义时，采用了开门见山直接了当的做法，用信息技术画出平面上到定点与到定直线距离相等的点的轨迹，然后建立标准方程，这种办法虽能使学生印象深刻，但焦点、准线空降式地出现显得突兀，不能与抛物线的截线定义融合。

笔者曾设想在丹德林（Dandelin）模型中进行几何论证。在丹德林模型中，抛物线的焦点是圆锥截面与球的切点，准线是母线在球面上的切点形成的平面与圆锥截面的交线。这种做法虽能实现从截线定义到解析定义的自然过渡，也切合知识的逻辑顺序，但没兼顾到知识发展的历史顺序，而且对教师运用信息技术（几何画板、Geogebra）能力、对学生空间想象能力和推理能力的要求都很高，实践中有一定难度。

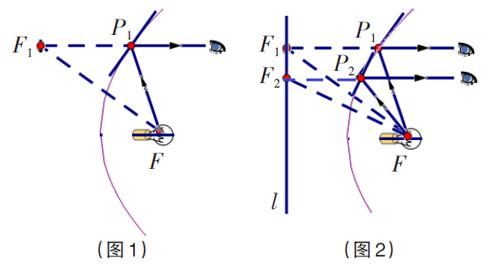
实际教学时，笔者利用了抛物线的光学性质来揭示焦点准线和建构解析定义。因为光学性质的运用如太阳灶、汽车车灯等是学生熟悉的生活情境，光的反射定律也为学生熟知。教学中，先让学生思考抛物线型太阳灶的工作原理：把平行于对称轴的太阳光经反射后汇聚于一点，此点即为抛物线的焦点。由光路可逆性，在焦点F处放置点光源，其发出的光线经反射后成为平行光，此为汽车车灯的工作原理。如下页图1，现设想一条光线射到抛物线镜上的点P1，经反射后进入人眼，那么“看到”的发光点在F1处，根据反射定律可知F1是F的虚像，它们关于反射面对称，反射点P1到F和F1的距离相等。若眼睛向下移动，如下页图2，人眼通过另一条反射光线“看到”F2处的虚像，这样，眼睛在移动过程中看到的虚像就排列在一条直线l上，该直线就是抛物线的准线。若把眼睛的上下移动与入射点P的运动对应，则动点P到定点F的距离与到定直线l的距离相等，其中F ? l。抛物线解析定义就在对自身视觉的抽象中得以建构，焦点准线和抛物线也自然融为一体，而且还兼顾了知识的历史顺序和学生的学习心理。

三、关于二次函数图象与抛物线统一性的教学

在初中教授二次函数时，教师以生活实例如拱桥、喷泉等外形特征来描绘图象形状，这是必要的也与学生认知契合。但若以此作为推理的起点则是不妥的，因为学生并未明白二次函数图象是抛物线的理论依据，获得的结论也没有建立在逻辑推理基础之上。所以，在高中教授抛物线标准方程时，有必要创设问题情境来激发探究实现演绎证明，笔者的教学过程如下。

片段1：“抛物线标准方程”的问题情境。

教师要求学生写出一个二次函数的解析式、画出图象、说明形状。学生展示后师生对话：“如何知道图象形状是抛物线的？”“之前老师告知的。”“能从二次函数呈现的信息（比如解析式和图象）找出其满足抛物线定义吗？”学生思索后表示不能，教师追问“如果知道了抛物线哪方面的特征，就能判断二次函数的图象是抛物线呢？”学生讨论后得出“需要知道抛物线焦点和准线间的代数关系，才能验证二次函数满足这种代数关系”。教师提出课题：抛物线的标准方程——焦点与准线的代数关系。

【设计意图】以学生写、画、说等动作唤醒其关于二次函数的记忆;通过师生对话引发认知冲突，明确建立抛物线标准方程的现实意义。从圆锥曲线的单元教学上看，建立抛物线的标准方程虽为教学重点但不是认知难点，因为可以借鉴和参考建立椭圆和双曲线标准方程的过程和方法。所以，从知识体系发现问题并用解析几何思想方法解决问题、发展和完善学生的认知结构才是抛物线标准方程的教学价值。

片段2：问题探究：证明二次函数y =  [14]  x2 的图象是抛物线。

学生将二次函数的解析式变形为抛物线的标准方程x2  =  4y，进而求出焦点坐标和准线方程，再依据定义验证。教师肯定其合理性，并指出这种从形式到形式的变形掩藏了推理过程中的逻辑链接，因此要求学生“在代数变形的过程中显示抛物线的焦点坐标和准线方程”。

学生无从下手，教师引导：根据抛物线定义，说明函数解析式中隐含了解析定义中的两个“距离”。因此，代数变形的方向应该与距离公式[（x-m）2+（y-n）2]靠近，注意到与之接近的是（x-m）2+（y-n）2这种形式（记为*），函数解析式中有这样的结构吗？如何变形为这种结构？

生1：由y =  [14]  x2 变形为4y =  x2，出现（x-0）2的形式，是（*）的局部，接下来设法将4y变成平方的形式，下面的变形还没有想好。

生2：将4y变形为（y+2）2-（y-2）2，得到（y+2）2-（y-2）2 =  x2，移项即得（y+2）2 = x2 + （y-2）2，再开平方即为[x2+（y-2）2] =│y+2│，满足定义。

师：很好！将二次项系数一般化，函数y =  ax2的（a≠0）图象是抛物线吗？

生3：由y =  ax2变形为x2 =  [1a]   y =  [4y4a] =（ y +  [14a] ）2 -（ y -  [14a]  ）2，即有[x2+（y-14a）2] =│y+[14a]│，焦點为（0，[14a]），准线方程为 y =-  [14a]  。

师：很好！一般形式y =  ax2 +bx+c的抛物线，能找出焦点坐标和准线方程吗？

学生4用配方的方法，但两分钟仍未得出结果，笔者示意观察配方得出的y -  [4ac-b24a]  = a（ x +  [b2a] ）2 与y =  ax2 形式上的差异性，他豁然明白“整体代换”，令x'= x +  [b2a] ，y '= y -  [4ac-b24a] 即有y' =  ax'2 ，所以焦点为（-  [b2a] ，  [4ac-b2+14a] ），准线为y =  [4ac-b2-14a]。

【设计意图】学生先将解析式转化为标准方程得出焦点和准线再验证，这是代数形式的等价变形，在逻辑上成立，但在思维上有“投机取巧”之嫌。布尔巴基学派早就指出，每个数学工作者都知道，单是验证了一个数学证明的逐步逻辑推导，却没有试图洞察获取这一连串推导的背后意念，并不算理解了那个数学证明。所以，教学中有必要要求学生在代数变形的过程中显示抛物线的焦点与准线，这实际上指出了变形的路径：寻找符合几何关系的代数结构，是一种深层次的数形结合。

需要特别指出，探究活动的顺利进行与课堂上推导抛物线标准方程时沿用了法国数学家洛必达《圆锥曲线分析》中“和差术”的示范铺垫密切相关。有研究者对比古今中外21套教材，发现其中10套采用“和差术”，其步骤如下：

建立如图3所示的坐标系 ，设动点P（x，y）到定点F（[P2]，0）与定直线l∶x =-  [P2]的距离相等（其中P是大于0的常数），过点P分别向x轴、定直线l作垂线，垂足分别为R，Q，直线l与x轴的垂足为S。由抛物线定义得PQ=PF，在Rt△PRF中有PF2=PR2 +RF2，所以有PQ2=PR2 +RF2，由PR=y，RF=x -  [P2]，PQ=x +  [P2]得（x +  [P2]）2=  y2 +（x -  [P2]）2，化简即得 y2 =2px。

笔者以为，洛必达的“和差术”是数形结合的典范，将线段PF视为Rt△PRF的斜边，虽然丧失了动点的完备性，但却直观地表达了距离的数学本质;线段PR和PQ长度的对偶表示，赋予了代数结构的对称美，对提升学生兴趣、改变“解析几何就是死算”的偏见具有积极意义。

四、总结

数学知识往往以学术形态呈现在教材中，教学时需将其转化为教育形态才能激发学生火热的思考，而将数学史融入教学是实现转化的重要途径。笔者通过梳理“抛物线”的研究脉络，结合学生的数学基础和认知特点，将数学史资源剪接整合，融入问题情境，以提升学生兴趣和促进学生学科核心素养的发展。当然，如何理解和证明抛物线图形的相似性，如何引入距离的运算促进圆锥曲线统一定义的形成，如何在抛物线教学中深化变量几何的思想方法等问题，还有待于进一步的研究与实践。

【参考文献】

[1]李大永.基于数学思想方法的理解，整体设计解析几何的教学[J].数学通报，2016（11）：13-18.

[2]史宁中.数形结合与数学模型[M].北京：高等教育出版社，2018.

[3]徐章韬，陈林.数学命题的认识及其课堂教学设计[J].课程·教材·教法，2014，34（11）：81-85.

[4]汪晓勤，沈中宇.数学史与高中数学教学——理论、实践与案例[M].上海：华东师范大学出版社，2020.

[5]陆琳琰.抛物线的发生教学研究[D].上海：华东师范大学，2013.

[6]阿波罗尼奥斯.圆锥曲线论：卷I-IV[M].朱恩宽，等，译.西安：陕西科技出版社，2007.

（注：本文系第32届江苏省“教海探航”征文获奖文章，有删改）