落实“大概念”教学理念

2021-04-22华志远

教育研究与评论（中学教育教学） 2021年1期

华志远

摘要：为了落实培养学生数学学科核心素养的新课标理念，人教A版高中数学新教材注重“大概念”视野下的“大单元”“大主题”设计，以彰显数学的整体性、系统性和联系性。比较新旧教材中三角函数的定义，分析新教材中三角函数定义变更的意图，进而设计与实施新教材中三角函数定义的教學，并且进一步反思“大概念”教学理念的内涵与价值。

关键词：“大概念”教学;高中数学新教材;三角函数定义

2020年秋学期，无锡市作为普通高中新课程新教材实施国家级示范区，开始在高一年级使用依据《普通高中数学课程标准（2017年版）》编写的人教A版高中数学教材（以下简称“新教材”）。为了落实培养学生数学学科核心素养的新课标理念，新教材注重“大概念”视野下的“大单元”“大主题”设计，以彰显数学的整体性、系统性和联系性，克服当下数学教学中普遍存在的知识碎片化、方法单一化及认识表层化问题。对此，新教材不仅在知识点的顺序和归类上做了比较大的调整，而且在知识点的具体内容上也有一些改动。“三角函数的概念”便是一个典型的例子：新教材不仅将其所属的“三角函数”单元从与“平面向量”单元、“解三角形”单元邻近（在前），变为与“函数的概念与性质”单元、“指数函数与对数函数”单元邻近（在后），而且对其定义也有所变更，从而凸显“函数”“建模”等“大概念”的串联整合（渗透体现）作用。

本文重点比较新旧教材中三角函数的定义，分析新教材中三角函数定义变更的意图，进而设计与实施新教材中三角函数定义的教学，并且进一步反思“大概念”教学理念的内涵与价值。

一、新旧教材中三角函数定义的比较

以往，几乎所有教材都是从锐角三角函数的定义出发，先将直角三角形放置到平面直角坐标系xOy中，从而得到基于坐标化思想的正弦、余弦及正切定义。再将锐角推广到任意角α，从而得到三角函数的定义：若α的终边过点P（x，y），记r=OP=x2+y2，则sinα=yr，cosα=xr，tanα=yx（x≠0）。得到这一定义后，依据相似三角形的边对应成比例，得出：α的正弦、余弦及正切值只与α的终边有关，而与点P的位置无关。也就是说，只要α确定，它的正弦、余弦及正切值就确定了。于是，它们都是关于α的函数，可以分别称为正弦函数、余弦函数和正切函数。然后，从一般到特殊，在单位圆中引进三角函数线，为后续学习同角三角函数关系、诱导公式、三角函数的图像与性质、两角和与差的三角函数等内容提供便捷的几何工具。

这样的定义编写注重了数学本身的逻辑性，但是相应地，抽象程度比较高，与学生的认知水平不匹配。教学中，教师倘若照本宣科，学生就会只知其然，而不知其所以然。具体来说，学生可能产生以下困惑：初中锐角三角函数的定义为什么要推广到任意角？推广时又为什么要放置到平面直角坐标系中？推广后的定义是否科学、合理？以前学习的函数只有一个自变量，为什么三角函数有两个自变量？哪个是自变量，哪个是因变量？对此，教师需要挖掘概念发生的背景或现象，通过高水平的问题情境设计及师生互动，才能搭建起学生的认知支架，让学生弄清楚知识的来龙去脉，逐步抽象建构概念。此外，三角函数线的学习必须补充有向线段及数量的概念，显得比较麻烦。

新教材则是从建立刻画周期性变化现象的数学模型（单位圆⊙O上的点P以点A为起点做逆时针方向旋转，建立一个数学模型，刻画点P的位置变化情况）出发，在前一节用任意角的概念刻画点P的位置变化情况的基础上，进一步建立平面直角坐标系xOy，通过角α的终边与单位圆交点P坐标的求解，得出三角函数的定义：设α是一个任意角，α∈R，它的终边OP与单位圆相交于点P（x，y），则y叫作α的正弦函数，即y=sin α;x叫作α的余弦函数，即x=cos α;y与x的比值叫作α的正切函数，即yx=tan α（x≠0）。然后，从特殊到一般，通过例题，将基于单位圆上点的定义推广到一般情形，得到基于终边上任意一点的定义，为后续学习三角函数的实际应用和在其他数学分支中的应用（如摩天轮的旋转、简谐振动、波，复数的三角式、极坐标、二阶矩阵刻画的旋转变换等）做好铺垫。

这样的定义编写关注到数学产生的现实性，显得更为直观和简洁，便于学生记忆和理解：在运动思想（旋转变换）、函数思想（定义及性质）及数学建模（用数学模型刻画圆周运动这一周期现象）三个“大概念”的统摄下，基于任意角的概念，利用单位圆上点的坐标，得出关于单个自变量的函数模型，体现三角函数定义的科学性、合理性和发展性，同时自然地省略了三角函数线的内容。此外，也注意了两种定义的互相转化，保证了学生概念理解的丰满、完善。

综上，从数学的本质上看，两种定义是等价的，但是，从教学的效能上看，新教材的定义更为高效。

二、新教材中三角函数定义的教学

（一）探究建构

师为了学习三角函数，前面学了任意角和弧度制，将角的范围扩大到全体实数。借助这些知识，我们进一步研究上一节开头提出的问题：（出示图1）如图，单位圆⊙O上的点P以点A为起点做逆时针方向旋转，记∠AOP=α，则α与点P的位置有什么关系？

生只要α确定，点P的位置就唯一确定了。

师也就是说，可以借助α的大小变化刻画点P的位置变化。那么，在平面内，点P的位置如何更精确地刻画？

生建立直角坐标系，点P的位置可以用坐标（x，y）表示。

师如何建立直角坐标系？

生以O为原点、OA为x轴的非负半轴。

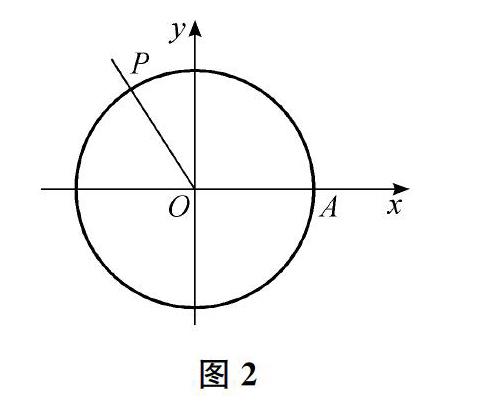
师好的。（出示图2）那么，给出α，能否说出点P的坐标？

（学生思考。）

师比如，α分别取0、π2、π、3π2、2π。