基于MB-LBP和张量HOSVD的人脸识别算法

宋艳萍，黄 华，库福立，樊丹丹

(新疆农业大学 数理学院，新疆 乌鲁木齐 830052)

0 引 言

近年来，人脸识别一直是模式识别和计算机视觉领域中的研究热点和难点，并且在众多领域中有着广泛的应用。然而，在不易受控的条件下如何提升人脸识别算法的识别精度和鲁棒性等仍是需要深入研究。

在人脸识别研究中，特征提取是提高人脸识别精度的关键技术。目前，主要有全局特征和局部特征方法[1]，其中，全局特征法可以表示人脸轮廓、肤色和人脸特征等完整的结构信息，但在不易受控的复杂光照、表情、姿态等条件下，其识别效果会随之下降；局部特征法可提取人脸图像的纹理等局部特征信息，这类方法有局部二值模式、Gabor变换以及方向梯度直方图法等，在面对不易受控条件下具有更强的鲁棒性。目前，基于不同特征提取算法提出的人脸识别方法有：主成分分析[2,3]、判别分析[4]、反射感知模型[5]、局部二值模式法[6-9]、Gabor滤波器法[10]、张量的图像识别方法[11-13]和基于深度学习的人脸图像识别方法[14-16]等。

不同的识别算法各有优缺点，其中，局部二值模式是基于图像纹理的描述算子，具有灰度不变性、旋转不变性等优点；基于张量的人脸识别算法，利用张量工具可以更有效地表示高维数据，同时，张量奇异值分解是一种完全数据驱动的分解方式，能有效提取多维数据中的结构特征。因此，本文利用局部二值模式和张量工具研究人脸识别问题，通过优选不同尺度MB-LBP算子组合，融合多尺度分块局部二值模式和张量高阶奇异值分解提出一种人脸识别算法，并进行算法验证分析。

1 多尺度分块局部二值模式(multi-scale block local binary patterns，MB-LBP)

局部二值模式(local binary patterns，LBP)是一种描述图像局部纹理特征的算子[7,8]，存在过于局部化、易受噪声影响等不足。基于此，Sheng等[8]在LBP算子基础上提出了MB-LBP算子，其核心思想是将LBP算子中的单个像素点用该子区域块的平均灰度值进行替换，每个子区域都是包含相邻像素的方形块。比如，3×3的区域块，MB-LBP 算子的单位区域尺度为 9×9的矩形块，则MB-LBP算子表达式可表示为

(1)

其中，ic，ip分别表示中心区域块的平均灰度值、第p个相邻区域块的平均灰度值，且

对此，MB-LBP算子运算过程，如图1所示。

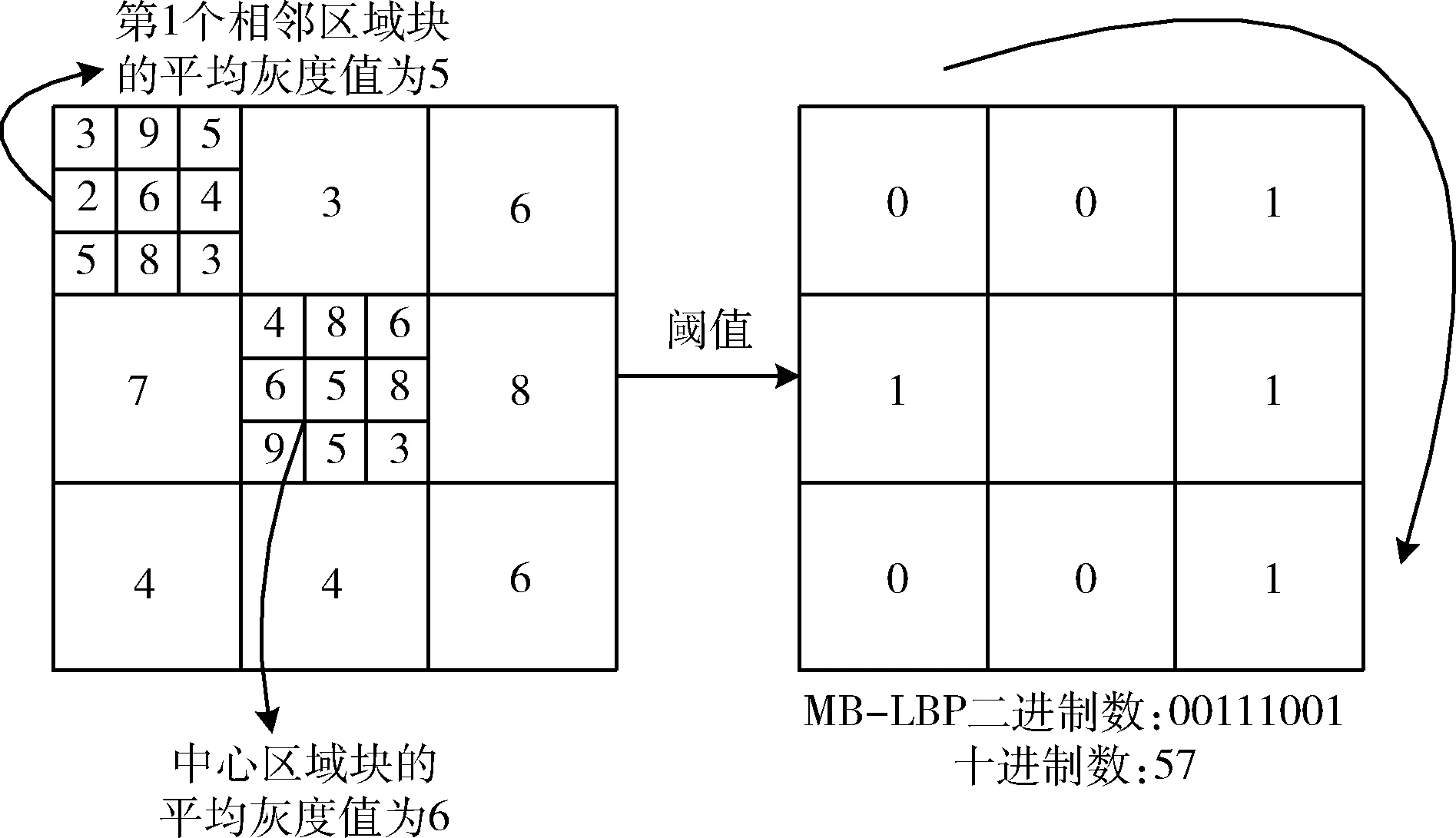
图1 基本的MB-LBP算子运算过程

一般地，将区域尺度为S×S的MB-LBP算子简记为MBS-LBP算子。MB-LBP算子利用子区域块的平均灰度值代替单个像素点，提取到的特征信息能有效抑制噪声的干扰，并且还可以描述不同尺度的纹理特征信息。如图2所示，给出了人脸图像MB3-LBP、MB6-LBP、MB12-LBP算子的滤波结果。

图2 不同尺度的MB-LBP算子滤波人脸图像

从图2可以看出，小尺度MB-LBP算子可以提取出人脸图像的局部特征和微观特征，而大尺度MB-LBP算子的滤波结果降低了噪声的影响，鲁棒性更好，可以为小尺度MB-LBP算子提供辅助信息，但是大尺度MB-LBP算子也丢失了一些重要的人脸识别信息。因此，在具体应用中，应当优选不同尺度的MB-LBP算子组合，然后将提取的特征信息进行融合，以期获得更好的识别效果。

如图3所示，选取一个小尺度MB5-LBP算子、一个大尺度MB13-LBP算子分别提取人脸图像的特征信息，特征融合后得到该人脸图像的特征向量。在此，利用MB-LBP算子对人脸图像进行特征提取，必然面临提取的人脸图像纹理特征维数过高。此时，若直接将提取的纹理特征用于人脸识别，势必会增加识别算法的计算复杂度，增加计算量，并且识别效果也会很差，因此，在建立人脸识别分类算法时，需要对人脸图像的纹理特征进行降维预处理。

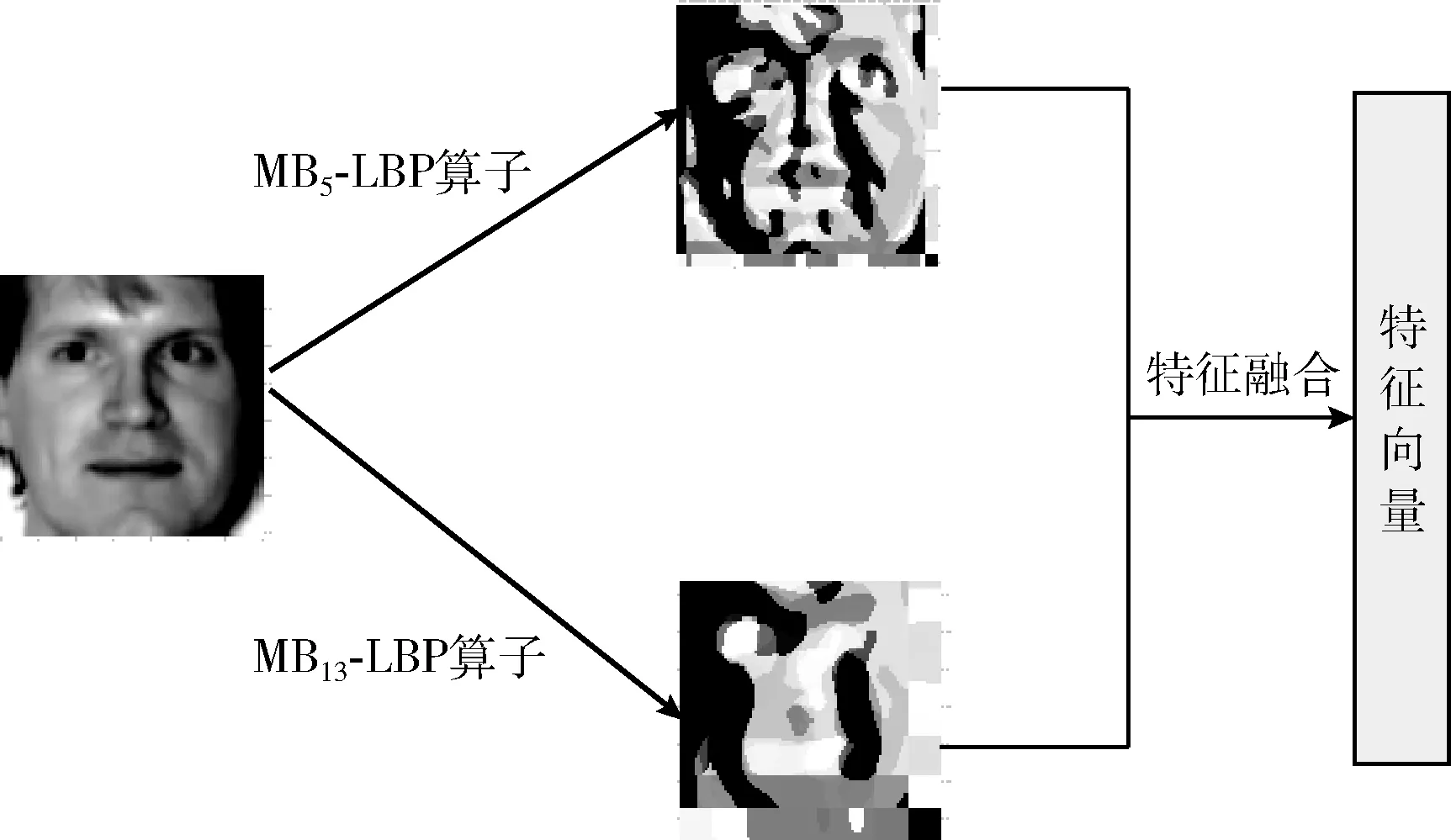
图3 人脸图像的多尺度MB-LBP算子特征提取

2 张量和张量奇异值分解

2.1 张量的基本概念

本文所谓的张量特指多维数组，是矢量和矩阵的推广，比如标量可称为0阶张量，向量称为1阶张量，矩阵称为2阶张量，而3阶张量可以理解为数据存放呈现三维长方体形式。

2.2 张量奇异值分解

目前，将矩阵的奇异值分解(singular value decomposition，SVD)推广到张量，提出了不同的分解算法，比如：张量CP分解，它是将张量分解成若干个秩一张量之和的形式；张量Tucker分解，它是将张量表示成一个核心张量沿着每一个模式乘以一个矩阵的形式，Tucker分解也常称作高阶奇异值分解(high-order SVD，HOSVD)。

A=S×1U(1)×2U(2)…×NU(N)+E

(2)

图4 三阶张量的HOSVD

对于HOSVD算法，利用交替最小二乘法，通过最小化误差函数

寻求最优解，是一种更加有效的高阶正交迭代算法(higher order orthogonal iterative algorithm，HOOI)[19]。本文将采用该方法进行张量高阶奇异值分解。

3 基于MB-LBP和张量奇异值分解的人脸识别算法

3.1 人脸图像的高阶张量表示

首先，需要根据人脸图像构建张量。本文将不同光照、不同背景、不同姿态等均视为不同表情，所以构建的是三阶张量，其中，第一模态表示像素模态，第二模态表示表情模态，第三模态表示人物模态。

3.2 基于张量奇异值分解的人脸识别分类器

A≈S×1U(1)×2U(2)×3U(3)

(3)

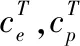
(4)

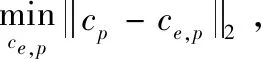
3.3 人脸识别算法流程

本文提出的人脸识别算法流程如下：

步骤1 将人脸数据库划分为训练集和测试集；

步骤2 根据训练集的人脸图像，优选不同尺度的MB-LBP算子组合，提取图像纹理特征向量，并构造训练集人脸图像的3阶张量模型；

步骤3 利用HOOI算法对训练集人脸图像的3阶张量进行高阶奇异值分解；

步骤5 输入测试图片，利用识别分类器，判断测试图片所属的类别。

4 实验结果与分析

为验证本文算法的有效性，选取Yale数据库、自制数据库作为实验数据库，其中，Yale数据库是由耶鲁大学制作的经典人脸数据库，自制数据库是由本课题组自制的人脸数据库。表1列出了两个人脸数据库的相关信息。在此，对人脸数据库进行样本划分，一部分作为训练样本，一部分作为测试样本。其中，Yale数据库的训练样本是从15个人物中的每个人物随机选取6个表情，每个人分别剩下的5个表情为测试样本；自制数据库的训练样本是从6个人物中的每个人物随机选取4个表情，每个人分别剩下的两个表情为测试样本。

表1 两个人脸数据库的相关信息

仿真实验平台为 Windows 7(64位)操作系统下的Matlab 2016b。硬件配置为Intel(R) Core(TM) i3-3110M CPU@2.40 GHz，NVIDIA GeForce 610M独立显卡，6.00 GB内存，2 T硬盘。

4.1 Yale数据库的识别结果分析

为了优选MB-LBP算子组合，本文首先根据训练集的人脸图像，利用3至16共14个单尺度分块局部二值模式提取训练集人脸图像的纹理特征，并基于HOSVD构建人脸识别算法分类器，然后利用测试图片进行检验，计算分类器的识别精度。

如图5所示，可以得出，小尺度MB-LBP算子的识别精度均优于大尺度MB-LBP算子，说明进行人脸图像的特征提取时，局部特征和微观特征更有利于人脸识别效果；另外，小尺度MB5-LBP算子的识别精度最高，等于97.333%；大尺度MB10-LBP算子、MB11-LBP算子、MB12-LBP算子、MB13-LBP算子的识别精度均等于90.667%，这说明大尺度MB-LBP算子提取的纹理特征也具有一定的识别能力。

图5 不同尺度构建的人脸识别分类器的识别精度

基于此，将大尺度MB-LBP算子提取的纹理特征作为小尺度MB-LBP算子的辅助，优选不同尺度MB-LBP算子组合，最终优选两个尺度MB5-LBP算子和MB13-LBP算子用于提取人脸图像的纹理特征，并进行特征融合。此时，根据训练集人脸图像构建3阶张量，其维数为20000×6×15，利用HOOI算法进行HOSVD，并进一步构建得人脸识别分类器，最后得到本文提出的人脸识别算法的识别精度为98.667%。如图6所示，为部分测试图片的识别结果(其中第一行为原测试图片，第二行为对应的识别结果)。

图6 部分测试图片的识别结果

为了比较算法的有效性，分别实现tensor HOSVD、LBP-tensor HOSVD、MB5-LBP-tensor HOSV、MB13-LBP-tensor HOSVD、MB5-MB13-LBP-tensor HOSVD以及两种深度学习算法(传统卷积神经网络(convolutional neural networks，CNN)和LBP-深度置信网络(deep belief networks，DBN))。如表2所示，本文提出的基于多尺度MB-LBP和张量HOSVD人脸识别算法与LBP-DBN算法的识别精度一样高，等于98.667%。同时，因为本文的算法需要融合多尺度分块局部二值模式提取图像的纹理特征，所以时间消耗上也稍多于其它算法，但是相比于深度学习算法LBP-DBN又略有优势，主要原因是深度学习算法在模型的训练上的时间消耗较长，并且还与实验环境的配置有关。

表2 不同人脸识别算法的识别精度与运行时间(Yale数据库)

4.2 自制数据库的识别结果分析

利用自制人脸数据库进行实验。首先，根据训练样本优选不同尺度MB-LBP算子组合，结果优选的两个尺度为MB4-LBP算子和MB15-LBP算子；然后，根据识别算法流程，依次构建3阶张量、HOSVD和构建人脸识别分类器。实验结果见表3，基于训练样本，本文的算法精度与LBP-DBN精度一样，都为100%，但是时间消耗上却有明显的优势。如图7所示，为部分测试图片的识别结果(其中第一行为原测试图片，第二行为对应的识别结果)。

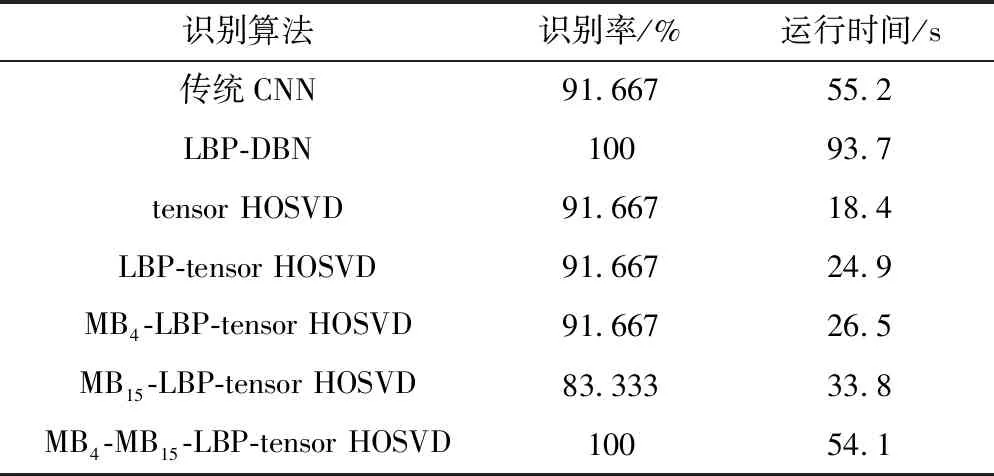
表3 不同人脸识别算法的识别精度与运行时间(自制数据库)

图7 自制数据库的部分测试识别结果

4.3 算法复杂度分析

本文提出的人脸识别算法是融合多尺度分块局部二值模式和张量高阶奇异值分解。该算法的复杂度主要在于MB-LBP算法和张量HOSVD算法，其中，LBP提取图像纹理特征具有较低的计算复杂度，但进行多尺度分块融合，在一定程度上会增加计算复杂度；张量奇异值分解，若在张量展开后直接进行SVD分解，其复杂度几乎等于o(n3)，特别是在融合MB-LBP算子后图像特征维度增长的情况下，直接实现SVD分解将非常耗时。而本文利用HOOI算法通过寻求优化函数的最优解实现张量HOSVD，相比于直接SVD分解，算法复杂度得到了有效解决，特别是在内存不足时处理高维数据的高阶张量分解，其优势更为明显。当然，若在提升硬件配置的同时，利用并行计算予以实现，则算法的时间消耗将得到更好解决，这也是下一步的研究打算。

5 结束语

本文提出基于多尺度分块局部二值模式和张量高阶奇异值分解的人脸识别算法。该算法基于多尺度分块局部二值模式，可以提取不同尺度的纹理特征信息；基于张量及张量奇异值分解，为处理不易受控条件下的人脸图像数据提供一种构建高维数据和模型的思路。最后，人脸数据库的验证结果表明，本文提出的人脸识别算法是一种有效的、可行的识别算法。但是，相比如当前流行的深度学习算法，本算法需进一步探索降低算法的计算复杂度，使其满足大数据背景下的复杂性和时效性。