基于仿生感知的机床刀具故障诊断系统
2021-04-22姜守坤
刘 富, 宋 阳, 刘 云, 康 冰, 姜守坤, 侯 涛
(吉林大学 通信工程学院, 长春 130022)
0 引 言
随着生产效率、 自动化程度不断提高, 数控机床设备愈加复杂, 工业生产中常因微小故障而引发连锁反应[1], 轻则造成设备损坏、 加工成本浪费, 重则危及人身安全[2]。作为与工件直接接触的加工设备, 刀具的日常磨损不可避免, 如无法及时发现刀具故障, 必将影响数控机床的加工精度, 进而造成严重的经济损失[3]。刀具故障诊断技术通过实时获取刀具运行信息, 快速并精确诊断出刀具存在的故障, 对降低次品率、 节约资源等具有重要意义[4]。因此, 对刀具故障诊断系统进行研究具有十分重要的现实意义。
刀具故障诊断方法包括直接测量法和间接测量法。直接测量法诊断精度较高, 但对环境要求较为严格, 并且需要离线检测, 无法实时判断刀具状态[5]。间接测量法通过提取生产过程中振动信号[6-8]、 力信号[9]和声发射信号[10]等特征判断刀具状态。间接测量法比直接测量法精度稍有下降, 但可实现实时在线监测。
王玫等[11]使用小波包分解方法处理切削力信号, 得到各频带上能量信号并将其作为刀具磨损状态的特征; Elangovan等[12]提出了一种基于决策树的振动信号刀具磨损预测算法, 使用十折交叉验证评估决策树算法生成的预测模型的准确性, 最大分类准确率为87.5%; Zhan等[13]采用经验模态分解的方法处理刀具振动信号, 并使用支持向量机算法建立故障诊断模型, 将刀具故障诊断准确率从82.5%提升到90.01%; Luo等[14]提出一种基于振动信号脉冲响应预测机床故障的方法, 采集了288 d的机床振动信号, 从信号样本中提取脉冲响应, 并建立深度学习模型诊断数控机床的动态特性, 在实验中取得了97%的预测精度, 但这种长期检测方法在工业环境应用存在局限。除单一信号检测外, 多传感器融合决策[15-17]分析的方法也有进展, 宁倩[18]以振动信号和切削力信号作为原始信号, 获得了与铣刀磨损程度具有映射关系的特征量, 采用支持向量机对特征进行分类, 预测精度可达81.48%; Huang等[19]提出一种基于重构时间序列卷积神经网络的方法, 通过对刀具力信号、 振动信号和声发射信号进行融合决策, 结果表明该方法预测误差为几微米。总体而言, 多信号融合决策分析方法复杂, 多传感器安装难度较大, 而振动信号广泛用于单信号和多信号故障诊断系统中。
虽然刀具故障诊断系统研究取得了较大进展, 但仍然存在系统庞大、 精度低、 成本高等问题。为此, 笔者提出一种基于仿生应变传感器的数控机床刀具故障诊断系统。首先将精度高、 价格低的仿生柔性裂纹阵列振动敏感元件封装成刚性的应变传感器, 以保护元件的结构, 使其能有效采集刀具振动信号, 采用小波包分解去除信号中的环境噪声。然后归一化并提取刀具振动信号时域和频域特征, 最后通过支持向量机算法建立刀具故障诊断模型。在机床刀具离线故障诊断和在线故障诊断中验证了笔者设计的基于仿生应变传感器的机床刀具故障诊断系统的有效性, 并与现有几种故障诊断系统成本进行了对比。结果表明, 这种新型故障诊断系统保证了故障诊断性能, 降低了检测成本。
1 基于仿生应变传感器的刀具故障诊断系统
基于仿生应变传感器的刀具故障诊断系统分为硬件系统和软件系统两部分。硬件系统通过封装仿生柔性裂纹阵列振动敏感元件检测刀具振动信号, 并通过采集电路上传到上位机进行存储分析; 软件系统主要通过信号处理方法, 对刀具振动信号进行预处理, 之后提取信号的时域和频域特征, 通过支持向量机训练刀具故障诊断模型。
1.1 硬件系统
图1为硬件系统示意图。

图1 硬件系统示意图Fig.1 Hardware system diagram
硬件系统的作用是采集机床刀具的振动信号, 其主要由仿生应变传感器、 惠斯通电桥、 差分放大电路、 STM32数据采集板和上位机组成, 封装后的仿生应变传感器用于检测刀具振动信号, 信号经惠斯通电桥和差分放大电路差分放大后, 通过STM32数据采集板传输到上位机。在本系统中, 信号采样频率为1 000 Hz。
1.1.1 仿生柔性裂纹阵列振动敏感元件
仿生柔性裂纹阵列振动敏感元件是受蝎子腿部关节处狭缝状感受器感知机理启发, 开发的一种柔性应变传感器[20]。蝎子(见图2a)是夜行动物, 主要依赖分布于腿部关节处的缝感受器(见图2b)感知附近猎物运动的振动信号, Han等[21]通过模仿蝎子缝感受器的结构, 在柔性材料聚二甲基硅氧烷(PDMS: Polydimethylsiloxane)表面制备了规则可控的裂纹阵列。图2c为仿生柔性裂纹阵列振动敏感元件的生物缝感受机理, 当有振动信号产生时, 分布在敏感元件表面的微裂纹阵列将受到挤压或拉伸, 此时裂纹宽度将发生改变, 其表面金原子接触面积发生改变, 传感器电阻发生变化。该仿生振动敏感元件(见图2d)具有微米级检测精度, 制备成本低(5元/个, 为相同精度传感器的千分之一)。

图2 仿生柔性裂纹阵列振动敏感元件生物原型、 生物感知结构、 仿生敏感元件感知机理及元件实物Fig.2 Biological prototype, sensing structure and entity of the vibration sensitive component based on bionic flexible crack array
1.1.2 仿生应变传感器封装
数控机床加工过程中, 废料、 冷却液的溅射会破坏仿生柔性裂纹阵列振动敏感元件的结构, 所以笔者设计了元件阵列悬空粘贴的方法对仿生柔性裂纹阵列振动敏感元件进行封装, 制备仿生应变传感器。封装装置分为基座和保护外壳, 材料均为铝合金。基座设计为支撑式结构, 如图3a所示, 基座底部设有两个支架, 支架位于底板对称的位置, 并在中间形成凹槽, 将仿生柔性裂纹阵列振动敏感元件主体部分平置于基座支架上, 两端绝缘部位粘贴到基座支架顶端, 使裂纹阵列处于悬空状态, 支架和元件整体形成了两端支撑、 阵列悬空的结构。支撑式基座结构的优势在于, 当刀具振动通过基座支架带动仿生柔性裂纹阵列敏感元件振动时, 其上的裂纹阵列受到挤压和拉伸, 支架间凹槽给柔性敏感元件的裂纹阵列提供了形变的空间。为验证支撑式基座结构的信号采集效果, 将其与平台式基座(见图3b)结构进行了对比, 支撑式与平台式基座封装结构上仿生柔性裂纹阵列敏感元件电压变化曲线如图3c所示, 可以看出, 两端支撑式基座结构使仿生柔性裂纹阵列敏感元件在检测中电压的变化范围更大, 更有利于振动信号采集。

图3 支撑式与平台式基座及相应仿生柔性裂纹阵列振动敏感元件电压变化曲线Fig.3 Voltage curve of bionic flexible crack array vibration sensitive component on supporting and platform bases
仿生柔性裂纹阵列振动敏感元件及完整的封装装置如图4所示。支撑式基座与保护外壳安装为一体, 保护外壳可以有效保护仿生柔性敏感元件, 其一侧与支架高度平行的位置有两个供元件电极线通过的小孔, 仿生柔性敏感元件的电极线从小孔引出后, 小孔处及外壳与基座接缝处通过热熔胶密封, 冷却的热熔胶可以防止检测过程中导线抖动对检测结果造成影响, 也可有效避免数控机床加工过程的冷却液喷溅对仿生柔性敏感元件造成破坏。

图4 仿生柔性裂纹阵列振动敏感元件及封装装置Fig.4 Vibration sensitive component based on bionic flexible crack array and packaging device
1.2 软件系统
刀具故障诊断的软件系统流程框图如图5所示, 首先采集刀具正常工作时和故障工作时的振动信号, 建立刀具振动信号数据库, 然后进行信号去噪处理, 消除环境噪声的干扰, 并归一化, 最后提取信号时域和频域特征, 并采用支持向量机算法建立刀具故障诊断模型。

图5 软件系统流程框图Fig.5 Flow chart of the software system
1.2.1 信号去噪
为去除刀具信号中掺杂的环境噪声, 笔者采用小波包分解方法去噪。小波包分解方法是在传统小波分解[22-23]的基础上, 对信号高频成分与低频成分进行十分精细的分解, 在处理非稳态、 包含有高频成分的刀具振动信号时具有很好的效果。小波包变换公式为

(1)
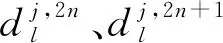
笔者选取不具有对称性的dbN小波作为母小波。dbN小波的特点是: 当阶数N增加, 消失矩阶数变大, 频域局部化能力变强, 频带划分效果变好, 信号光滑性变好, 但阶数变大会降低系统实时性。本实验选择db10作为母小波对刀具振动信号进行3层小波包分解。刀具正常工作的振动信号如图6a所示, 刀具故障时的振动信号如图6b所示。小波包去噪结果如图7所示,图7a为去噪后的正常刀具振动信号,图7b为去噪后的故障刀具振动信号。
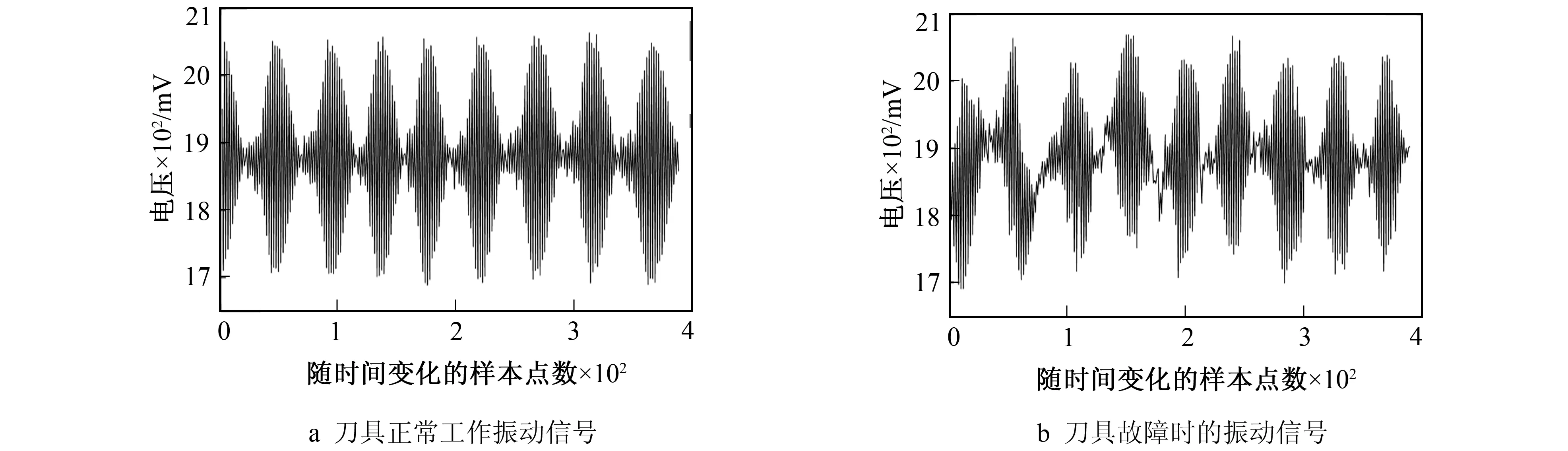
图6 检测刀具振动信号Fig.6 Vibration signal of tool

图7 去噪后的振动信号Fig.7 Vibration signal after denoising
1.2.2 归一化
笔者采用最大最小归一化方法归一化数据, 消除样本中突变信号的干扰。最大最小归一化方法对原始数据进行线性变换, 将数据值映射到[0,1]区间, 最大最小归一化的转换函数为

(2)
其中xmax为样本点最大值,xmin为样本点最小值,x为每个样本点的值,x*为归一化的值。
1.2.3 特征提取
笔者提取刀具样本信号的时域和频域特征, 对刀具状态进行辨识以验证故障诊断系统的有效性, 其中时域特征共有11个, 包括最大值、 峰-峰值、 均值、 均方根值、 峭度、 方差、 标准差、 波形因子、 峰值因子、 脉冲因子和峭度因子, 频域特征共有3个, 包括均方频率、 重心频率和频率方差, 时域和频域特征组成14维的特征向量空间。
1.2.4 故障诊断模型
笔者主要研究判断刀具运行状态的问题, 其关键在于正常刀具信号与故障刀具信号的二分类问题, 选择在处理高维度、 非线性的二分类问题上表现不错的支持向量机(SVM: Support Vector Machine)方法, 进行故障模型训练。支持向量机仅需少量的数据样本, 就可以达到很好的分类效果。笔者将信号的时域和频域特征用于支持向量机算法训练刀具故障模型。
1.2.5 评价指标
在故障诊断过程中可能会出现以下4种情况:
真阳性(TP: True Positive,TP): 样本的真实类别是正例, 预测结果为正例。
真阴性(TN: True Negative,TN): 样本的真实类别是负例, 预测结果为负例。
假阴性(FP: False Positive,FP): 样本的真实类别是负例, 预测结果为正例。
假阳性(FN: False Negative,FN): 样本的真实类别是正例, 预测结果为负例。
为验证故障诊断系统的有效性, 需对故障诊断模型的诊断效果进行评估。笔者选取准确率(Accuracy,A)、 精确率(Precision,P)、 召回率(Recall,R)和F1值(F1 score,F)作为故障诊断模型的评价指标, 其中准确率是预测正确的样本数占所有样本比例; 精确率是针对预测结果, 表示预测为正的样本中有多少是真正的正样本; 召回率是针对原来样本, 表示样本中的正例有多少被正确预测。F1值是准确率和召回率的加权调和均值。准确率和召回率出现极端情况时会影响F1值, 使F1值变小。综上, F1值可以综合反映整体的指标, F1值越大时, 说明分类模型效果越好。
4个评价指标的计算公式如下所示
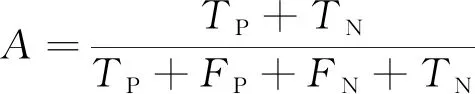
(3)
(4)

(5)

(6)
2 实 验
2.1 实验场景
笔者选择台群TS-100数控机床(主轴12 000 r/min)的刀具作为故障诊断对象, 该数控机床主要生产宝马汽车喷油嘴零部件, 刀具故障类型为后刀面磨损故障。笔者将封装后的仿生应变传感器安装在数控机床刀台上, 连接采集电路, 对目标刀具进行为期20 d的连续监测振动信号, 上位机以时间格式存储刀具振动信号。在实验过程中, 共采集到22.4 GByte的振动信号数据, 在信号采集过程中, 人工记录刀具的工作时间范围、 刀具发生故障及刀具更换的时间节点和故障类型等详细信息。笔者根据上述信息截取刀具工作时的振动信号构成样本库, 每个信号样本包含58 401个样本点, 共选取了150个信号样本建立振动信号数据库, 其中刀具正常工作样本100个, 刀具故障工作样本50个。图8为实验机床与仿生应变传感器。

图8 实验机床与仿生应变传感器Fig.8 Experimental machine tool and bionic strain sensor
2.2 实验结果与分析
2.2.1 模型参数选择
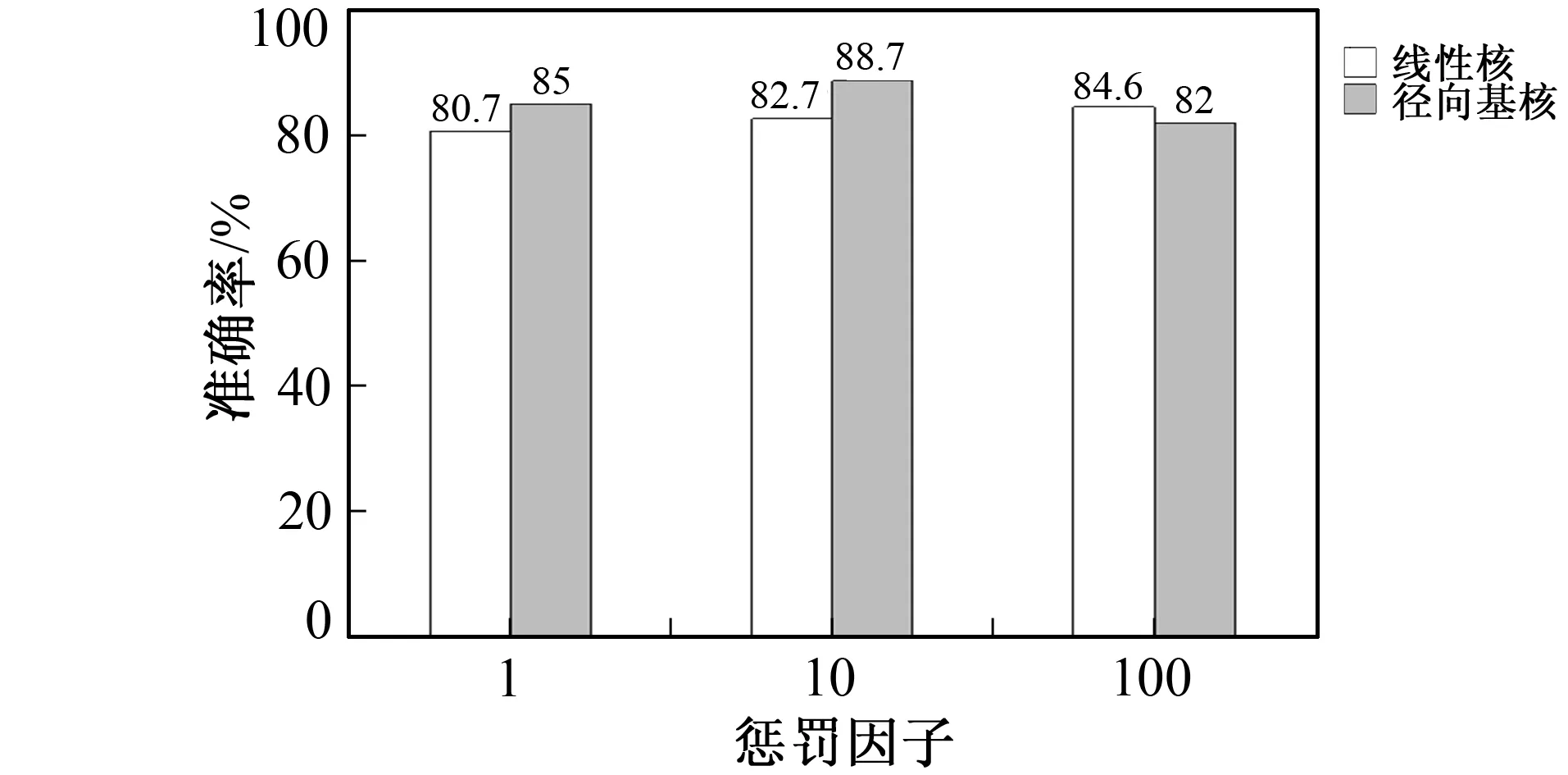
图9 核函数及惩罚因子对系统的影响Fig.9 The influence of kernel function and penalty factor on the system
笔者选择支持向量机建立故障诊断模型, 要选择适当的核函数和惩罚因子, 选择线性核函数和径向基核函数, 并设置不同的惩罚因子, 对振动信号数据库中的信号样本进行诊断, 不同核函数和惩罚因子的诊断结果准确率作为选择参数的标准, 选择的参数及相应的准确率如图9所示。可以看出, 线性核在处理刀具信号上, 效果不如径向基核函数, 所以选择局部性强、 对大样本和小样本都有较好性能的径向基函数作为支持向量机的核函数。而惩罚因子C越大, 对分错样本的惩罚程度越大, 因此在训练样本中准确率越高, 但会降低模型的泛化能力, 降低测试数据的分类准确率。相反, 若减小C值, 则容许训练样本中有一些误分类错误样本, 增强模型的泛化能力。根据图9结果, 笔者将惩罚因子C设定为10。
2.2.2 离线故障诊断
将正常信号和故障信号两类样本的时域和频域特征作为支持向量机的输入, 使用径向基核训练模型, 训练过程中采用10折交叉验证方法, 将处理后得到的150个信号样本平均分为10组, 选择其中的9组作为训练集, 剩下的1组作为测试集, 并重复10次, 以确保每组数据都进行了训练和测试。最后将10次故障诊断准确率、 精确率、 召回率和F1值的平均值作为最终的性能评价指标。笔者提出的故障诊断模型的性能如图10, 表1所示。
从计算结果可以得出, 预测模型10次离线故障诊断的平均准确率为89.1%, 精确率为89%, 召回率为95.4%, 在准确率、 精确率和召回率较高的同时, F1值达到了92.1%, 证实了基于仿生应变传感器的故障诊断模型可以有效判断机床刀具的状态。
表2为笔者的刀具故障诊断系统与已有刀具故障诊断系统中所用方法、 传感器参数及性能对比。由表2可知, 笔者所提出的刀具故障诊断系统的准确率优于文献[12]、 文献[18]的方法, 而与文献[13]相比, 故障诊断精度稍显不足。但笔者采用的仿生柔性裂纹阵列振动敏感元件的价格为其他系统中传感器的几百分之一, 极大的节约了刀具故障诊断系统的成本。

图10 故障诊断系统性能评价Fig.10 Performance evaluation of fault diagnosis system

表1 故障诊断系统性能评价Tab.1 Performance evaluation of fault diagnosis system

表2 几种刀具故障诊断系统对比Tab.2 Comparison of several tool fault diagnosis systems
2.2.3 在线故障诊断
为进一步验证笔者所提方法的有效性, 从采集到的刀具振动信号中选择5组连续的刀具工作信号, 其中共包含52个数据样本, 根据记录的故障发生时间节点设定每个样本的预期结果, 之后使用笔者建立的低成本刀具故障诊断系统对选择的连续刀具工作信号进行故障诊断, 刀具正常工作的信号样本表示为1, 故障信号的样本表示为0, 实际诊断结果如表3所示。由表3可见, 基于仿生应变传感器的刀具故障诊断系统对于在线故障诊断的准确率为88.5%, 可以有效诊断机加实时工况的刀具状态。
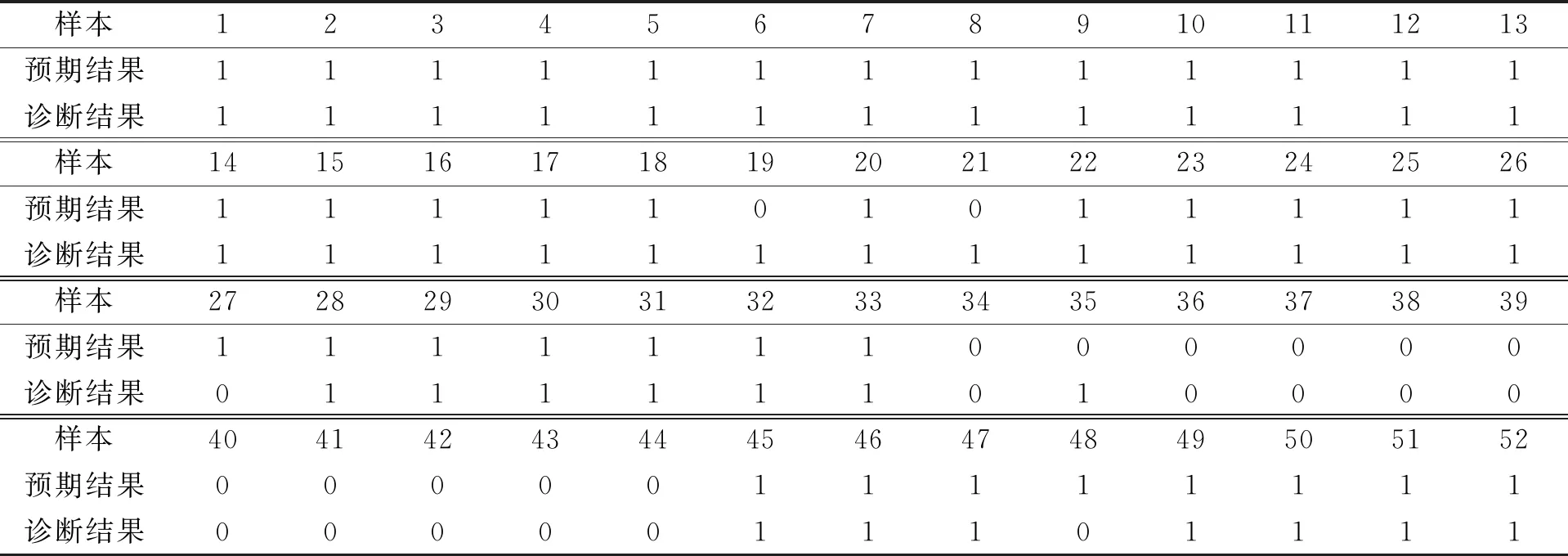
表3 诊断结果Tab.3 Diagnostic results
3 结 语
笔者提出一种基于仿生应变传感器的数控机床刀具故障诊断系统。该系统首先将灵敏度高、 成本低的仿生柔性裂纹阵列振动敏感元件封装成刚性的仿生应变传感器, 采集机床刀具振动信号; 然后建立刀具故障诊断模型对离线故障和实时机加环境下的在线故障进行诊断。结果表明, 笔者设计的基于仿生应变传感器的刀具故障诊断系统对机加故障诊断的准确率大于88%, 在保证故障诊断性能的同时降低了检测成本, 在一定程度上解决了现有刀具故障诊断系统存在的系统庞大、 成本高、 精度低的问题。未来将根据刀具不同运行阶段振动信号的特征, 准确判断刀具的实时运行状态, 并预测刀具更换的时间。
