基于PSO-FCM的长输管道泄漏检测方法

张 勇, 王 臣, 王 闯, 姜鑫蕾, 刘 洁

(东北石油大学 a. 物理与电子工程学院; b. 电气信息工程学院, 黑龙江 大庆 163318)

0 引 言

随着我国社会的快速发展, 工业生产和日常生活对石油天然气能源的需求量也日趋增加。油气长输管道作为石油千米、 天然气的主要运输方式, 具有低污染、 高效率的优点[1]。截止至2015年8月, 中国陆地油气管道总长达到12万千米, 包括原油管道、 成品油管道和天然气管道, 其中原油管道约2.3万千米, 成品油管道约2.1万千米, 天然气管道约7.6万千米[2]。管道会由于服役时间的增长而逐渐老化, 受到各种介质的腐蚀, 工作人员的操作失误或人为的破坏而发生泄漏事故。油气管道泄漏不仅会给生产、 运营单位造成巨大的经济损失, 而且会对环境造成破坏、 严重影响管道沿线居民的身体健康和生命安全。据统计, 自1995年-2017年, 我国共发生管道泄漏引起的安全事故1 000多起, 造成近千亿人民币的经济损失。目前, 长输油气管道泄漏检测方法按基于软件或硬件的方法划分主要有以下几种。基于硬件方法： 磁通泄漏检测法、 红外成像检测法、 管道机器人检测法以及放射性探伤检测法。基于软件方法： 声波检测法、 负压波检测法、 小波变化检测法、 流量平衡法、 实时模型检测法以及神经网络模型检测法[3-4]。在实际检测过程中, 由于受到自然地理环境的限制, 以上这些检测方法的准确率无法保证, 且检测效率低、 成本高。

模糊C均值算法由Dunn[5]提出, 并由James[6]改进完善的一种模式识别聚类算法。因其处理高纬度复杂样本的能力较强和其无标签的样本要求, 模糊C均值算法是目前最常用的聚类算法。传统的模糊C均值算法由于在根据目标函数优化聚类中心的过程中采用了梯度下降法, 其最终得到的聚类中心往往并非最优聚类中心, 在某些特殊情况下, 还会出现无法找到合适聚类中心的情况。而粒子群算法是一种基于群体的随机优化算法, 其具有收敛速度快, 全局搜索能力强, 寻优效果好的特点。

因此, 笔者提出了一种基于粒子群优化的模糊C均值聚类算法, 利用粒子群算法极佳的寻优特性替代传统模糊C均值中的梯度下降算法, 以提高模糊C均值算法的聚类能力, 并构建模型, 对长输气管道数据进行分析处理, 实现长输管道泄漏检测的目的。

1 模糊C均值算法

设待聚类样本点个数为N, 空间为X={x1,x2,…,xi},i∈[1,N], 聚类的类别数为C, 聚类中心为P={c1,c2,…,cj},j∈[1,C], 则样本空间中待分类的第i个样本点与第j个聚类中心之间的距离可表示为

Dij=‖xi-cj‖

(1)

设U为隶属度矩阵, 其中第i个样本点对第j个聚类中心的隶属度可表示为

(2)

其中m为任意大于0的整数, 一般取2, 其约束条件为对样本空间中的任意样本点i, 其对所有聚类中心的隶属度之和总为1, 可表示如下

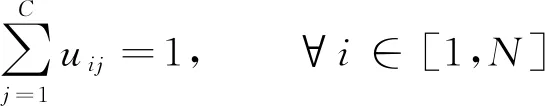
(3)

根据式(1)～式(3), 模糊C均值算法的目标函数J定义如下

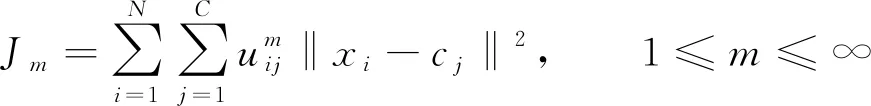
(4)

随着迭代的进行, 隶属度矩阵U和聚类中心P的更新公式如下

(5)

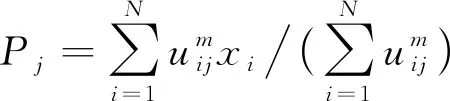
(6)

模糊C均值的迭代过程可以归结为以下几个步骤：

1) 确定类别数C, 参数m和迭代停止误差ε以及最大迭代次数M；

2) 初始化聚类中心P；

3) 计算初始距离矩阵Dij；

4) 根据隶属度矩阵更新公式更新隶属度矩阵, 如遇到样本点与聚类中心重合的情况, 则把该样本点相应聚类中心的隶属度设为1, 其余设为0；

5) 根据聚类中心更新公式更新聚类中心；

6) 重新计算距离矩阵, 并更新目标函数值；

7) 若达到最大迭代次数或前后两次迭代的目标函数值的差小于迭代停止误差

Jiter-Jiter-1≤ε

(7)

则停止迭代, 否则转到步骤4)继续进行迭代；

8) 将样本点划分为隶属度最大的那一类。

2 粒子群算法

粒子群(PSO: Particle Swarm Optimization)算法是由Kennedy等[7]提出的一种进化算法, 是一种基于种群的随机优化算法。粒子群算法是模仿昆虫、 兽类、 鸟类和鱼类的群体行为, 以协同的方式寻找猎物, 群体中的每个成员通过学习自身的经验和群体中其他成员的经验, 不断改变自己的运动趋势的搜索模式。

设粒子群的样本个数为n, 样本空间中第i个粒子的位置表示为xi, 第i个粒子在迭代过程中所经过的最好的位置被称为第i个粒子的个体最优解, 也叫局部极值点, 表示为pi, 整个群体所经过的最好的位置被称为群体最优解, 也叫全局极值点, 表示为pg, 第i个粒子在第k次迭代时的速度表示为vi(k), 粒子群中的每个粒子根据当前迭代次数时的个体最优位置和群体最优位置更新自己下一时刻的速度, 更新公式如下

vi(k+1)=ωvi(k)+c1r1(pi(k)-xi(k))+c2r2(pg(k)-xi(k))

(8)

可以看出, 速度的更新公式由3部分组成： 第1部分为前一时刻速度对下一时刻粒子局部搜索能力和全局搜索能力的平衡； 第2部分是粒子的自我学习部分, 根据自己的学习经验调节全局搜索能力, 避免陷入局部最优值； 第3部分是粒子的群体学习部分, 根据粒子群中其他粒子的学习经验调节局部搜索能, 实现粒子群中的信息共享。粒子速度通常设置限制为粒子搜索空间的宽度, 即

(9)

粒子位置更新公式如下

xi(k+1)=xi(k)+vi(k+1)

(10)

其中k为当前迭代次数。ω为惯性因子,c1和c2为加速度常数,r1和r2为两个在闭区间[0,1]上正态分布的随机数, 笔者采用权值线性递减法根据迭代次数更新ω的值, 更新公式如下

(11)

其中ω1和ω2为惯性因子的初始值和最终值,Q为当前迭代次数,Qmax为最大迭代次数。

权值线性递减法的引入使粒子群算法在迭代开始时具有较强的全局搜索能力, 扩大了搜索空间, 确保粒子尽快收敛到最优解所在区域, 随着迭代次数的增加,ω值逐渐减小, 此时粒子群算法局部搜索能力增强, 便于找出全局最优解[8]。

根据实际问题设置粒子群算法的适应度值计算公式, 设第i个粒子在第k次迭代时的适应度值为Fi(k), 第k次迭代时群体适应度值为Fg(k), 第k次迭代时第i个粒子的个体最优适应度值为Fibest(k), 第k次迭代时的群体最优适应度值为Fgbest(k), 则迭代过程中第i个粒子的个体最优位置更新公式如下

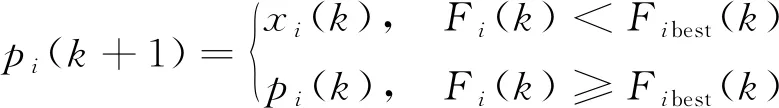
(12)

群体最优位置更新公式如下

(13)

粒子群算法的寻优迭代过程可以归结为以下几个步骤：

1) 初始化粒子位置P, 根据初始化粒子位置计算初始pg、pi、Fgbest、Fibest, 根据搜索空间X的宽度, 初始化粒子速度v, 设置速度限制[vmax,vmin], 根据实际问题设置适应度值函数F, 适应度阈值ε；

2) 根据速度更新粒子位置；

3) 根据更新的粒子位置计算当前迭代时刻的Fi(k)、Fg(k), 并根据个体最优位置更新公式和群体最优位置更新公式计算下一时刻的个体最优位置和群体最优位置；

4) 若达到预设的最大迭代次数或群体适应度值小于预设的适应度阈值ε, 则结束迭代过程; 否则转到步骤2)继续迭代过程；

5) 所得的群体最优位置即为所求问题的最优解。

3 基于粒子群算法的模糊C均值聚类算法

3.1 分 析

传统的模糊C均值算法是一种依赖梯度下降搜寻最优解的算法, 而梯度下降算法全局搜索能力很弱, 对最优解的搜寻主要依赖于自身的局部搜索能力。算法本身对初始化聚类中心的质量要求较高, 且搜索空间, 即样本点的数量不能过大, 否则会严重影响最终的聚类结果, 通常需要对同一组样本点进行很多次实验才有可能得到满意的聚类结果, 这样算法耗费的时间较多, 且工作效率极低。

而粒子群算法是一种基于群体的随机寻优算法, 对所求解的初始位置要求不高, 全局搜索能力强, 且不易陷入局部最优值, 对数量较大的复杂样本处理能力极强。近些年很多学者利用粒子群算法的这些优点, 将其用于优化传统的经典算法, 进而解决了许多实际工程中的问题[9-15]。因此笔者将模糊C均值算法看作是样本点对目标函数最小值求解的问题, 采用粒子群算法替代传统模糊C均值算法的迭代过程, 得到一种性能更好的聚类算法。

3.2 参数设置

将模糊C均值所求聚类中心P矩阵作为粒子群算法的粒子群,P(k)=(p1,p2,…,pC)为粒子群算法第k次迭代时的聚类中心矩阵,p1,p2,…,pC为此时的聚类中心, 模糊c均值的样本点所围成的区域作为粒子群算法的搜索空间, 搜索空间宽度即为粒子群算法的速度限制[vmin,vmax], 其中vmin=-vmax,vmax为模糊C均值样本点区间宽度, 模糊c均值的目标函数Jm作为粒子群算法的群体适应度值函数, 将Jc定义为粒子群的个体适应度值函数

(14)

其意义为某一聚类中心c相对于全体样本点的距离与隶属度值的乘积, 适应度值越低, 所得聚类中心的聚类效果越好。当群体最优值小于预定的ε值或达到最大迭代次数时, 中止迭代过程, 得到模糊C均值算法所求最优聚类中心。

3.3 迭代过程

迭代过程归结为以下几个步骤:

1) 给定预设参数m, 聚类样本点X, 预置聚类类别数c；

2) 在样本空间X中初始化粒子群位置P, 初始化粒子群速度v, 同时通过适应度值公式计算得到初始个体最优适应度值和群体最优适应度值；

3) 根据粒子群速度v更新粒子群位置P, 并根据个体适应度值函数和群体适应度值函数更新此时的粒子群个体适应度值、 群体适应度值、 最优个体适应度值、 群体最优适应度值；

4) 根据个体最优适解更新公式和群体最优解更新公式更新个体最优解和群体最优解；

5) 根据速度更新公式更新粒子群速度v；

6) 若达到最大迭代次数或群体适应度值小于预设值ε, 则迭代结束, 否则转到步骤3)继续进行迭代；

7) 所得群体最优解即为模糊C均值算法所求最优聚类中心；

8) 根据所得聚类中心计算样本空间中各样本点的隶属度值, 将样本点划分为隶属度较大的那一类。

4 管道泄漏检测数据处理实验

为了验证笔者所提出的算法模型的有效性和优越性, 将提出的算法模型用于对管道泄漏检测实验数据的分类, 将实验数据进行分类并用传统的模糊C均值算法、 经典的3层BP神经网络算法构建模型对同一组实验数据重复多次进行相同的实验, 比较所得的结果, 作为衡量算法有效性和优越性的标准。

4.1 实验数据

本次实验所用的数据采集自东北石油大学复杂系统与先进控制研究院长输管道泄漏检测实验平台。实验平台管道有效长度为181.2 m, 管道型号为DN80, 材质为不锈钢, 管壁厚度4 mm, 管道上配有18个模拟泄漏点(其中14个为手动泄漏点, 4个为自动泄漏点), 均匀分布在180 m的管道上(每隔10 m设置一处泄漏点), 管道两端分别配有压力传感器、 液体流量计、 气体流量计及温度传感器, 这些传感器在试验过程中以1 024 Hz的频率采集数据, 当管道运行状态正常时采集的数据为正常数据, 打开泄漏点时采集的数据为泄漏数据。

实验平台工作状态如下： 管道内介质为空气, 压强为0.4±0.05 MPa, 模拟泄漏点为14号手动泄漏点。最终采用的数据为二维数据(进口压力值、 出口压力值), 样本数为3 072, 其中1 477个为管道运行状态正常的数据样本, 其余1 595个为管道发生泄漏时的数据样本,图1为实验平台的工作原理图。

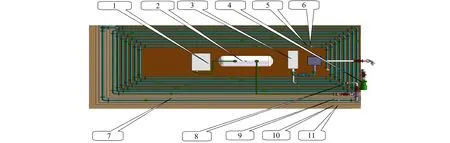
1. 气泵; 2. 储气罐; 3. 储水罐; 4. 水泵; 5. 出口温度传感器; 6. 出口压力传感器; 7. 模拟泄漏点; 8. 出口气体流量计; 9. 进口气体流量计; 10. 进口温度传感器; 11. 进口压力传感器。图1 实验平台原理图Fig.1 Layout of experiment platform

4.2 实验结果

实验所用数据容量为3 072个, 为有标签数据, 笔者提出的基于粒子群优化的模糊C均值算法以及传统的模糊C均值算法在建模分类时采取无标签分类的方式, 经典的3层BP神经网络在训练过程中采用有标签的训练方式, 每种算法进行20次实验, 其聚类和分类的平均准确率和最佳准确率如表1所示。

表1 实验结果Tab.1 Experiment result

分别选取PSO-FCM(Fuzzy C-Means based on Particle Swarm Optimization)算法和传统FCM算法在20次实验中聚类效果最好的一组实验, 对比其适应度值随迭代次数变化曲线, 结果如图2所示。3种算法模型在20次实验中的具体准确率及其变化趋势如图3所示。

从图2可看出, 笔者提出的PSO-FCM算法相较于传统的FCM算法, 适应度值迭代到最优值的速度更快, 最终得到的最优适应度值更小。从图3可以看出, 3种算法模型中, 笔者提出的PSO-FCM算法对管道泄漏数据的平均检测准确率最高, 且检测准确率最为稳定, 波动最小, BP神经网络虽然检测准确率的变化波动也很小, 但准确率较PSO-FCM平均低了近6%, 而传统的FCM算法虽然最高识别准确率达到了96.29%, 但平均准确率较低, 识别效果缺乏稳定性, 波动太大。

图2 适应度值随迭代次数变化曲线 图3 实验结果Fig.2 The fitness mean varies according to iteration times Fig.3 Experiment Result

5 结 论

根据以上实验结果, 得出以下结论。

1) 笔者提出的基于粒子群优化的模糊C均值聚类算法相比于传统的模糊C均值算法, 聚类速度更快, 聚类效果更好, 其对复杂数据聚类问题的适应性更好。

2) 基于笔者提出的改进模糊C均值聚类算法建立的模型, 对长输管道实验数据的聚类效果优于目前应用广泛的3层BP神经网络分类模型, 且其聚类效果稳定, 可以进一步应用于实际工作环境中验证其可行性。