降落伞拉直过程的动力学仿真与试验

2021-04-22史文辉陈允浩盛思佳

科学技术与工程 2021年8期

史文辉，陈曦*，陈允浩，盛思佳

(1.南京理工大学机械工程学院，南京 210094； 2.宏光空降装备有限公司，南京 210022；3.陆军装备部驻南京地区第一军事代表室，南京 210024)

无人机(unmanned aerial vehicle, UAV)是利用无线电遥控设备和自备的程序控制装置操纵的不载人飞机，或者由车载计算机完全地或间歇地自主地操作的航空器[1]。无人机常用的回收方式有伞降回收、撞网回收、自行着陆回收和绳钩回收等[2]。其中，伞降回收由于总体布置简单、质量小、对其他系统依赖度低等特点被广泛采用[3]。无人机伞降回收主要分为如下几个阶段：①无人机平稳飞行；②伞舱打开，降落伞拉直；③降落伞充气；④无人机降落。其中，降落伞拉直阶段和降落伞充气阶段一直是航空领域的研究热点。相比于降落伞充气阶段，拉直阶段的研究更加困难，因此关于降落伞拉直阶段的研究文献较少。但是，降落伞的拉直过程本质属于绳系动力学，而关于绳系动力学的研究近年来一直是一个热点[4]。

降落伞的拉直过程短暂而又复杂，涉及十几个动作。对于该过程的研究最早出现在20世纪70年代。McVey等[5]提出了连续拉直模型，该模型假设拉直过程中伞绳始终处于直线状态，计算得到的拉直力与实际较为符合。Shen等[6]建立了火星减速系统的6自由度数学模型，并加入追踪控制率，对火星进入、下降与着陆(entry, descent and landing,EDL )任务中进入段和降落伞减速段的系统全弹道进行了仿真分析。Enrique等[7]基于填充时间膨胀模型和Ludtke的面积定律，精确计算在降落伞打开期间的结构载荷和应力。

Yang等[8]分析了降落伞的拉直过程建立了多质点动力学模型，重点考虑了绳索的柔性大变形特性，运用有限元方法建立了回收系统拉直过程的均匀连续体拉出模型，并进行了仿真实验。张青斌等[9]，王海涛等[10]对绳索的弹簧阻尼模型、绳索的多刚体模型和绳索的连续模型分别进行了系统研究，研究了尾流对伞包的轨迹影响，并用于降落伞拉直阶段的计算和分析中，得到了较好计算结果。

目前中外学者对降落伞的拉直方式集中在传统的牵顶伞牵引和弹射释放等成熟方式，对于其他牵引方式几乎没有研究，并且这些研究仅停留在理论层面，没有考虑降落伞初始折叠的状态。因此提出较为符合实际的折叠模型，全面考虑降落伞的初始位置关系与折叠状态，并采用创新性的火箭牵引降落伞的方式，以期为满足中国无人机平台回收需求、结合统一型无人机开展无人机回收系统的研制提供理论依据，并为后续开展火箭牵引降落伞模型建立、降落伞充气等工作奠定基础。

1 有限元理论

降落伞拉直过程体现了绳索和伞衣大位移、大变形的非线性特点。ABAQUS以其强大的处理非线性问题的能力而著称，因此，利用ABAQUS中的膜单元和桁架单元分别对伞衣和伞绳进行建模，降落伞拉直过程的数值仿真利用非线性有限元软件 ABAQUS的显示动力学模块实现[11-13]通过ABAQUS/Explict模块对进行动力学仿真。

1.1 膜单元有限元理论

膜单元是可以承受膜力但无弯曲或横向剪切刚度的薄板，因此膜中唯一非零应力分量是平行于膜中间表面的那些分量，即膜处于平面应力状态。通过对结构离散化和网格划分，可得到四节点四边形单元的组合体。在局部坐标系下，由有限元法的理论假设可知[14]，具体为取膜单元任意一个节点的位移向量为d，

d={u,v,w}T

(1)

式(1)中：u、v、w均为整体坐标系中3个坐标方向的函数。因此，对于该膜单元在局部坐标系下的位移可以表示为

x={xi,yi,zi,xj,yj,zj,xm,ym,zm,xn,yn,zn}

(2)

则膜单元的节点位移可以表示为

d={ui,vi,wi,uj,vj,wj,um,vm,wm,un,vn,wn}

(3)

对于四边形单元，形函数在局部坐标下可表示为

N=[INi,INj,INm]

(4)

式(4)中：I为的单元矩阵，大小为4×4。

根据有限元理论，位移函数与节点位移之间的关系为

d=NxT

(5)

由于膜材料的非线性特性，采用Green应变张量，膜单元的应变矩阵B可以表示为

B=B0+BN

(6)

式(6)中：B0为应变矩阵的线性部分；BN为应变矩阵的非线性部分，它是节点位移向量d的函数。在此基础上使用虚位移原理，并且将有限元写成增量形式，具体表示为

(7)

式(7)中：K为整体刚度矩阵；d′为节点位移；P为K与d合并后向量；σ为典型第二类Piola-Kirchhoff应力张量。

由力学理论可知，B0与节点位移无关，因此可得

d′ε=d′(B·d)=B·d′d+

(8)

最终有限元增量方程可以表示为

(K+Kσ)·d′d=d′P

(9)

式(9)中：Kσ为几何刚度矩阵。

1.2 桁架单元有限元理论

对于大尺寸伞绳，可基于有限元法进行离散建模，将伞绳离散为数个绳段单元，每个绳段单元采用ABAQUS提供的桁架单元来模拟，桁架单元只能够承受轴向载荷，不能承受弯矩，与绳索承载类似[15]。每个桁架单元都能够承受运动过程中的内力和外力，因此整个伞绳的动力学模型可通过单个桁架单元的动力学方程组集得到[16-17]。如图1所示，桁架单元Hij两端节点分别为节点i和节点j，单元轴向力Tij的大小可表示为

图1 绳段张力Fig.1 Rope tension

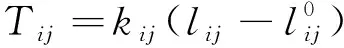
(10)

式(10)中：lij为单元Hij的当前长度；kij为单元Hij的等效刚度系数，由绳索材料决定，可表示为

(11)

伞绳在拉直过程中，绳段所受内力主要为绳段张力Tij，外力主要为万有引力Gij，大气阻力忽略不计。将单个绳段单元Hij受力等效到节点i上，受力情况如图2所示。记节点i的质量为mi，节点i的动力学方程可表示为

(12)

式(12)中:ui为节点i的位移；Ti为节点i所受张力；Gi为节点i所受万有引力。

图2 绳段受力Fig.2 The rope stress

2 ABAQUS仿真

2.1 模型分析

降落伞拉直过程是通过火箭药燃烧产生的持续推力将处于折叠状态的伞衣和伞绳逐渐拉出到拉直的过程，通常分为顺拉法(先拉伞衣)和倒拉法(先拉伞绳)两种[18-19]。由于倒拉法需要更小的最大拉直力，因此采用倒拉法[20]。具体拉直过程如图3所示。

图3 火箭牵引降落伞拉直过程Fig.3 The deployment process of parachute towed by rocket

降落伞在使用时，会按照预设形状折叠嵌入伞衣套内，并根据伞舱的尺寸二次折叠放入伞舱内。伞衣套顶部伸出连接带与火箭底部连接，伞绳底部同样设置连接带与无人机连接。当遇到紧急情况需要快速降落时，火箭在收到点火指令发射，火箭推进剂燃烧产生的持续推力牵引伞衣套带动伞衣和伞绳逐渐脱离伞舱，伞衣和伞绳受到向上的拉力和向下的重力，逐渐趋于拉直状态。当伞衣和伞绳被拉直后，火箭由于推力和惯性牵引伞衣套继续运动，防止对伞衣和无人机产生破坏。同时，伞衣在气动力和无人机重力的作用下迅速充气展开，保证无人机平稳落地。

采用ABAQUS有限元软件进行拉直过程仿真，为便于模型建立和仿真计算，将模型进行简化处理。伞舱并不会影响整个拉直过程，因此模型中可以省略伞舱；伞衣套的主要作用是保护伞衣，防止伞衣提前充气，其本质和伞衣相同，在建模时可将伞衣套等效为伞衣建模，避免复杂和繁琐的建模过程。

伞衣折叠模型的建立是整个拉直过程中最复杂的部分，由于伞衣为大变形织物，无法直接建立折叠模型，因此可以先根据每个伞衣幅的尺寸建立单个伞衣幅模型，再根据各伞衣幅之间的位置约束关系，建立伞衣模型，最后伞衣的折叠关系建立伞衣折叠模型。

2.2 模型建立

以火箭牵引降落伞的拉直过程为研究对象进行仿真，降落伞采用平面圆形伞，如图4所示，采用“Z”型折叠，如图5所示，便于计算降落伞拉直到充气的整个开伞过程，具有非常重要的研究价值。

首先根据伞衣幅尺寸建立单个伞衣幅模型，然后根据各伞衣幅位置约束关系将单个伞衣幅堆叠放置，每个伞衣幅之间间隔一定的角度和距离，伞衣幅模型局部放大视图如图6所示。

图4 平面圆形伞示意图Fig.4 Circle flat parachute

图5 “Z”型折叠Fig.5 “Z”fold

图6 伞衣幅模型Fig.6 Canopy frame model

然后对上述伞衣幅模型进行分割，分割长度与伞衣在伞衣套内的折叠长度保持一致，从底层到高层依次放置，建立折叠在伞衣套状态下的降落伞几何模型。采用六面体自由化网格对伞衣进行网格划分。降落伞的几何模型和网格模型如图7所示。

图7 降落伞模型Fig.7 Parachute model

将折叠后的模型作为拉直过程降落伞的初始状态，在此基础上添加火箭、伞绳等部件，最终折叠状态下的降落伞的仿真模型如图8所示。对此状态下的降落伞进行拉直仿真研究。

图8 仿真模型Fig.8 Simulation model

2.3 主要参数

2.3.1 火箭主要参数

火箭主要由喷管、火箭药、燃烧室、点火具等构成，在仿真与试验结果中，涉及的主要参数为外形尺寸、质量和推力等。通过用游标卡尺、台秤对火箭外形尺寸和重量数据的测量，火箭的主要参数如表1所示。

表1 火箭主要参数

降落伞的拉直过程是由火箭推进剂燃烧产生的持续推力把降落伞从伞舱中拉出直至拉直，为了使得仿真结果与试验更加符合，必须得到火箭的推力数据，为此进行了火箭推力试验。推力试验由压力传感器、数据传输线和数据采集器组成。压力传感器为压电式压力传感器，使用过程中，火箭发动机作用在传感器敏感部位处，然后传递给压电晶体。在压电效应作用下，测试系统捕捉到产生的电信号变化，从而采集到压力数据。试验共点火6发，常温(20 ℃)2发、低温(-50 ℃)2发、高温(55 ℃)2发。试验环境温度为20 ℃，采样频率为10 kHz，采样时间为10 s。具体试验数据如表2所示。

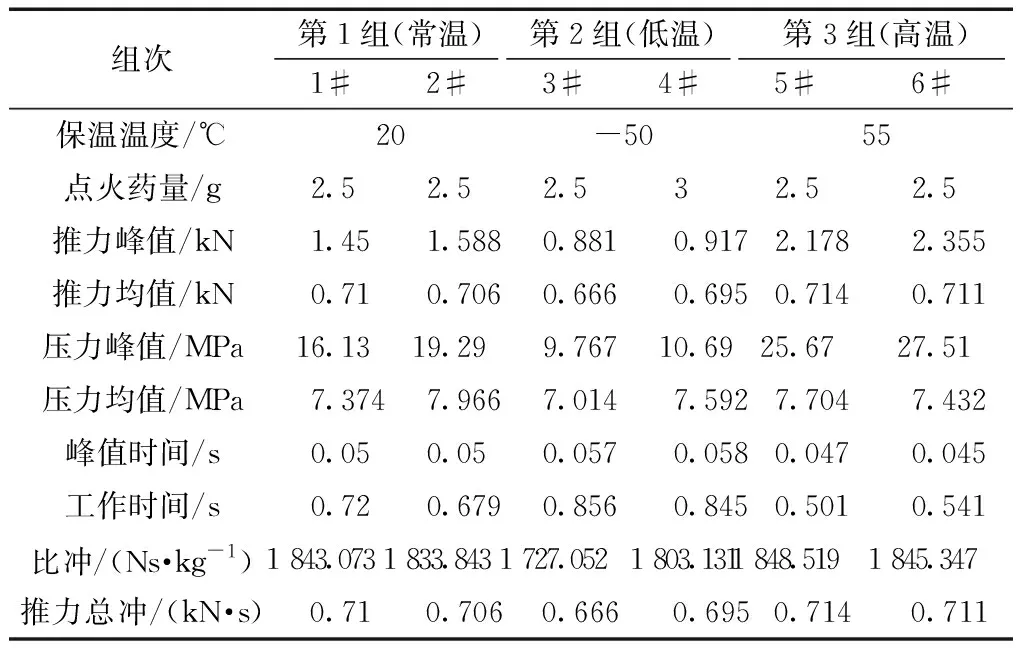
表2 火箭推力试验结果

2.3.2 降落伞主要参数

仿真模型选用的伞型为平面圆形伞，具体结构参数如表3所示。

表3 降落伞主要参数Table 3 Main parameters of parachute

降落伞模型材料参数的选择如下。

伞衣材料选用1056防灼锦丝绸材料，材料的密度为233.77 kg/m3，弹性模量为0.430 9 GPa，泊松比为 0.14，伞衣厚度为 0.000 1 m，假设伞衣材料为各向同性材料。

火箭牵引降落伞的连接带材料为25～1 000芳纶带，材料的密度588.1 kg/m3，弹性模量为130 GPa，加强带的横截面为矩形，面积为12.5×10-6m2，试验测得芳纶带的拉断力为19 860 N。

伞绳材料为2～200高强聚乙烯绳，密度为704.8 kg/m3，弹性模量为1.412 GPa，伞绳的横截面为圆形，面积9.62×10-6m2，试验测得高强聚乙烯绳的拉断力为2 000 N。

2.4 仿真结果

仿真模拟了火箭在-50 ℃、20 ℃、55 ℃状态下的降落伞拉直过程，火箭在55 ℃条件下拉直仿真过程如图9所示，伞衣和伞绳从刚开始的折叠状态逐渐被拉直，整个过程比较平顺，拉直效果比较好。

图9 拉直仿真过程Fig.9 Deploying simulation process

由表2可知，火箭在低温-50 ℃条件下，平均工作时间为0.850 5 s，平均推力峰值为0.899 kN，平均推力均值为0.680 5 kN；在常温20 ℃条件下，平均工作时间为0.699 5 s，平均推力峰值为1.519 kN，平均推力均值为0.708 kN；在高温+55 ℃条件下，平均工作时间为0.521 s，平均推力峰值为2.266 5 kN，平均推力均值为0.712 5 kN。由此可见，随着温度的升高，火箭工作时间降低，推力峰值和推力均值升高。

火箭的位移能直接反映出伞衣和伞绳的拉直程度。图10为火箭在不同温度下的位移。低温-50 ℃条件下，火箭在0.91 s时达到最大位移28.352 m；常温20 ℃条件下，火箭在0.80 s时达到最大位移29.110 m；高温55 ℃条件下，火箭在0.79 s时达到最大位移29.911 m。由此可得，随着温度的升高，降落伞的拉直时间变短，拉直长度降低。该结果符合火箭在不同温度下的工作时间和推力变化趋势。

图10 火箭位移曲线Fig.10 Curve of rocket displacement

由表2可知，火箭在低温-50 ℃条件下，推力峰值与推力均值差值的平均值为0.218 5 kN；在常温20 ℃条件下，推力峰值与推力均值差值的平均值为0.811 0 kN；在高温55 ℃条件下，推力峰值与推力均值差值的平均值为1.544 0 kN。由此可见，随着温度的升高，火箭推力峰值和均值的差值增加，推力曲线的波动越大。

图11、图12、图13分别为火箭牵引伞衣连接带、伞绳连接地面连接带和伞绳的受力曲线。在图11中，高温55 ℃时，在0.27 s连接带受力变化幅值最大为7 627.7 N；常温20 ℃时，在0.15 s连接带受力变化幅值最大为5 402.9 N；低温-50 ℃时，在0.18 s连接带受力变化幅值最大为5 712.5 N。

在图12中，高温55 ℃时，在0.71 s连接带受力最大为464.489 N；常温20 ℃时，在0.77 s连接带受力最大为458.892 N；低温-50 ℃时，在0.83 s连接带受力变化幅值最大为457.691 N。

在图13中，高温55 ℃时，在0.72 s连接带受力变化幅值最大为828.192 N；常温20 ℃时，在0.77 s连接带受力变化幅值最大为823.092 N；低温-50 ℃时，在0.80 s连接带受力变化幅值最大为464.645 N。由此可得，随着温度的升高，伞绳和连接带所受作用力的最大值增加，这对连接带、伞绳和伞衣材料的强度有更高的要求。该结果符合火箭在不同温度下的推力峰值和均值的差值变化趋势。

图11 火箭牵引伞衣连接带受力曲线Fig.11 Curve of rocket deploying canopy connecting belt

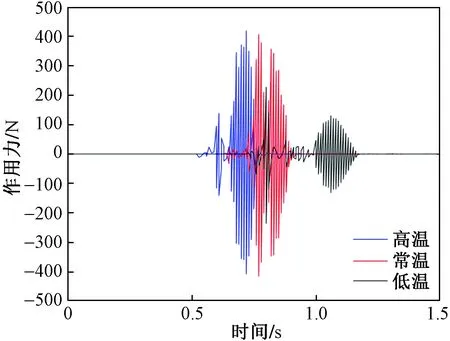
图13 伞绳受力曲线Fig.13 Curve of parachute rope

由以上分析可以看出，在高温55 ℃、常温20 ℃和低温-50 ℃ 3种状态下的火箭牵引降落伞的拉直过程中，随着温度升高，拉直所需时间变短，伞衣和伞绳的拉直长度变化幅度较小；伞绳和连接带受到的最大拉力值升高。

3 试验验证

为了验证仿真结果的正确性，设计了相应的地面试验，采用高温55 ℃状态下的火箭对降落伞进行拉直。为了便于试验记录以及避免环境因素对降落伞拉直过程产生影响，选择晴朗无风天气进行试验，试验布局如图14所示。通过航拍无人机悬空拍摄整个降落伞拉直过程，并记录时间。

火箭点火发射后，产生的持续推力将降落伞以及伞绳不断牵引出伞舱，随着火箭的持续上升，降落伞和伞绳被拉直。当火箭药燃烧完毕后，由于重力的作用，降落伞和火箭逐渐落向地面。试验过程中降落伞的拉直过程平稳有序，伞型较好，没有强烈扰动现象，如图 15所示。通过试验视频可知，从火箭点火到降落伞拉直，整个过程持续了0.70 s左右。

在高温55 ℃仿真结果中，火箭达到最大位移29.911 m用了0.79 s，时间误差为11.39%。伞衣的名义半径为7.78 m，当伞衣拉直后，测得伞衣的拉直长度约为11 m，伞绳长度为14 m，连接火箭与伞衣的连接带长度为1 m，连接伞绳与地面的连接带长度为5 m，火箭高度为0.36 m，因此火箭在理想状态下的位移约为31.36 m，总位移误差为4.62%。平均误差为8.005%。造成误差的原因主要是仿真中未考虑伞衣、伞绳和伞舱间的摩擦以及空气阻力等因素。

火箭牵引伞衣的连接带材料为25～1000芳纶带，试验测得芳纶带的拉断力为19 860 N。由高温55 ℃仿真结果可得，火箭牵引伞衣连接带受到作用力的最大值为7 627.7 N；伞绳连接地面连接带受到作用力的最大值为464.489 N，均小于芳纶带的拉断力值，符合使用要求。

伞绳材料为2～200高强聚乙烯绳，试验测得高强聚乙烯绳的拉断力为2 000 N。由高温55 ℃仿真结果可得，伞绳受到作用力的最大值为828.192 N；小于高强聚乙烯绳的拉断力值，符合使用要求。

通过仿真结果与试验结果的比较，发现在对应的时间内，仿真过程中的伞衣和伞绳的形状和位移与试验结果基本吻合。