路基冻胀对高速列车-轨道耦合系统动力特性的影响

蒙富佳， 唐先习， 刘 博， 王福久

(1.兰州理工大学土木工程学院， 兰州 730050； 2.中国铁路青藏集团有限公司西宁工务段， 西宁 810000)

21世纪初以来，高速铁路建设在中国飞速发展，高速铁路网已初步形成。与此同时，位于季节性冻土区[1-2]的高速铁路路基冻胀变形问题愈发突出。一方面会导致钢轨线性不平顺，破坏路基表面与支承层间的接触状态，另一方面，在高速运行的列车作用下，钢轨的不平顺激发了列车系统和无砟轨道的振动，加剧了轮轨相互作用，反过来助长了轨道的变形，这种恶性循环对行车的安全性和舒适性产生了不利影响，降低了铁路上相关结构的服役性能和使用寿命。目前，对于高速铁路路基冻胀的研究主要集中于形成机理上[3-5]，对路基冻胀造成铁路轨道的几何形态变化、列车安全性能的动力影响评价研究较少。所以，研究路基不均匀冻胀引起的轨道不平顺对高速列车-轨道结构耦合系统动力特性的影响尤为必要。

根据近几年兰新高铁冻胀路段的分布统计表明，路基冻害现象主要集中出现在门源至民乐一带，以路堤结构形式冻害为主，此路段路基冻胀引起了无砟轨道结构变形，严重影响了轨面的平顺状态和无砟轨道的结构性能，对行车安全有一定的威胁。在车辆-轨道耦合动力学研究初期，铁摩辛柯等[6]、Sato[7]学者大多采用质量-弹簧-阻尼组成的多刚体系统研究车轨动力学耦合，但模型等效变换的假设条件与实际车轨动力特征存在差异，随着列车内部结构在模型中不断细化，模型的计算结果也越来越接近实际值；高建敏等[8]研究了路基不均匀冻胀对高速列车系统动力响应的具体特征，认为系统动力响应幅值有较大的变化空间，同时探讨了轨道不平顺类型和行车速度对不平顺敏感波长的范围的影响；张鲁顺等[9]、郭毅[10]结合具体高速铁路路基冻胀的实际情况，研究了轨道结构变形特性、行车和轮轨动力响应效应。

在车轨耦合动力学理论的基础上，利用ANSYS有限元软件建立高速列车-轨道结构-路基耦合模型，通过编写命令流提取不同位置轮轨垂向力、轮重减载率、位移、加速度、支反力等数值。主要运用位移耦合法和位移接触法，位移耦合法主要提取车辆质量单元位移和加速度作为车辆的位移和加速度，还有钢轨梁单元节点的位移和加速度，位移接触法提取轮对质量单元与钢轨梁单元接触力即轮轨垂向力，然后根据轮轨垂向力计算轮重减载率。研究高速列车在路基典型冻胀、不同冻胀波长、不同冻胀峰值条件下对车体垂向振动加速度、钢轨动态位移、轮重减载率等系统动力特性的影响，以期为高速铁路冻胀区行车安全性和舒适性评估提供参考。

1 系统动力学模型

在高速铁路中，所有的子系统都是统一的整体，它们不是独立的系统，而是相互耦合、相互作用的关系，其中，列车、轨道与路基就是铁路轮轨系统中重要的组成部分。高速列车-轨道-路基系统耦合模型是通过轮轨相互关系和轨道-路基的接触关系将列车、轨道和路基3个子系统联结起来，在考虑路基冻胀变形影响的基础上，对列车系统和轨道系统的动力学特性进行评价，并根据模型运行结果分析轮轨相互作用特性。

1.1 高速列车-轨道-路基系统耦合模型

翟婉明[11]提出了车辆-轨道耦合动力学原理，抽象出高速列车-轨道-路基系统耦合动力学物理模型，如图1所示。高速列车采用具有10自由度的二系悬挂多轮对模型，同一般列车构造一样主要由车体、转向架、一系及二系悬挂减震弹簧与阻尼器、轮对组成。其中，βc表示点头自由度，图1中两处分别为车体点头自由度和转向架点头自由度。将钢轨简化为连续弹性离散点支承无限梁模型，采用Hertz非线性接触理论来描述轮轨之间法向的接触关系。为了考虑冻胀引起的支承层与路基间的脱空状态，两者之间同样要建立接触关系。

以CRH-3型高速动车组及双块式无砟轨道为研究对象，为了减小系统动力分析所需要的轨道长度，采用半车模型，即图1中A-A一侧的车体结构为车辆模型。CRH-3型车辆模型参数如表1所示。

图1 高速列车-轨道-路基系统耦合动力学物理模型Fig.1 Coupled dynamic physical model of high speed train-track-subgrade system

表1 CRH-3型车辆模型参数

1.2 耦合系统振动性能评价指标

路基冻胀引起高速列车和无砟轨道产生动力响应，一旦响应值超过任一系统动力学评价指标，就会对列车运行的舒适性甚至安全性产生影响。动力分析对象是高速列车-无砟轨道-路基耦合系统，由于无砟轨道的疲劳性能决定着轨道结构的服役寿命，所以除了考虑车辆运行的安全性和舒适性指标外，还应对比无砟轨道结构的动力性能指标[12-14]。该指标针对最高运行速度为200 km/h及以上的电力动车组，车辆结构运行安全与舒适性依据《高速动车组整车试验规范》，无砟轨道结构动力评价依据《高速铁路工程动态验收技术规范》，具体相关评价指标如表2所示。

表2 系统振动性能评价指标

2 冻胀变形对系统动力效应的影响

对兰新高速铁路门源地区的无砟轨道冻胀变形的监测结果统计显示，该路段路基冻胀量主要集中在20 mm以下，冻胀范围在35 m以内，结合两者的影响作用，在计算不同路基冻胀条件下无砟轨道的变形和受力情况所取的工况如下：冻胀波长分别为5、10、15、20、25、30、35 m；冻胀峰值分别为5、10、15、20 mm。

通过数据分析发现，该地区路基冻胀量集中在5～10 mm居多，冻胀范围以10～15 m居多，故可取冻胀峰值为10 mm、冻胀波长为10 m的工况为典型冻胀条件，列车时速按照兰新高速铁路的现运行最高速度250 km/h，以此来研究耦合系统的动力响应。

2.1 典型冻胀条件下对系统动力效应的影响

2.1.1 典型冻胀条件下车体动力响应特征

图2为在典型冻胀条件下，由于路基冻胀引起轮轨之间的竖向作用力变化和车轮轮重的减载情况以及半车模型车体竖向加振动速度沿轨道长度方向的变化情况。

图2 典型冻胀条件下半车模型车体响应Fig.2 Response of half car model body under typical frost heaving condition

从图2可以看出，在车体驶入和驶离冻胀区的过程中，轮轨的动力指标发生了变化。轮轨垂向力增加较大，轮轨之间的相互作用更加明显，两者接触力也明显增大，最大值达到了125.6 kN，对无砟轨道的损伤也逐步增加。随后由于相邻轮对和转向架的影响，列车进入冻胀峰值区后，轮轨垂向力会突然减载。轮重减载率反映车体的运行稳定性，而图2中显示的数值在冻胀中心附近较大，减载率最大峰值为0.14，但并未超限。这也是因为相邻轮对和转向架的影响使得轮轨发生减载现象，说明路基冻胀中心即冻胀峰值附近会对列车的运行安全有一定影响。

此外，在冻胀变形区，车体加速度开始发生剧烈变化。随着车体的逐渐驶入，轮轨相互作用增大，在各轮对与轨道结构的动力作用下，车体加速度先减小后增大，最终达到峰值，最大为0.18 m/s2。但在非冻胀路段没有明显的变化，这说明路基的冻胀变形对列车运行的舒适性有一定的影响。

2.1.2 典型冻胀下无砟轨道结构动力响应特征

路基冻胀变形对列车的稳定、安全产生有重要影响，同时，对于无砟轨道而言其影响也很明显。因此，选取了冻胀起始点、冻胀中心位置以及非冻胀位置处这3种特殊位置，对比分析典型冻胀条件下不同冻胀位置处的无砟轨道结构的动力响应情况。

图3为典型冻胀条件下3个位置处的钢轨和道床板竖向位移时程曲线。可以看出，在这3个位置处道床板和钢轨变化规律基本一致。即在未到达指定位置前道床板和钢轨竖向位移比较接近，而在车轮到达指定位置时，竖向位移急剧减小且变化幅度不同。究其原因主要是钢轨和道床板刚度不同所产生的响应也不同。

图3 不同位置处钢轨和道床板竖向位移时程曲线Fig.3 Vertical displacement time history curve of rail and track bed slab at different positions

通过对比发现，冻胀初期的钢轨的最大动态位移变化量为1.040 mm，道床板的最大动态位移变化量为0.057 mm，冻胀中心处钢轨的最大动态位移变化量分0.667 mm，道床板最大动态位移变化量0.037 mm，比非冻胀区的值分别大0.036 mm和0.001 mm。相对于冻胀中心和非冻胀位置处，冻胀起始位置位移变化更加明显，属于出现离缝现象可能性较大的区域。

图4为相同路基冻胀条件选定位置下钢轨和道床板的竖向加速度时程曲线。可以看出，当车轮经过3个位置时，钢轨和道床板的竖向加速度变化趋势相似，表现为接近指定位置时加速度开始激烈波动，远离指定位置加速度逐渐减小并趋于平缓，呈现出周期性的正(余)弦波形并且振幅不断减小，且相同位置下钢轨的竖向加速度先达到峰值。这是因为振动传递过程削弱了部分能量，钢轨和道床板产生了传递时差。对于钢轨和道床板而言，冻胀起始点最大竖向加速度分别为24.76 m/s2和6.49 m/s2，冻胀中心位置最大竖向加速度分别达到了10.83 m/s2和3.93 m/s2，非冻胀位置处最大值分别为10.90 m/s2和3.64 m/s2，结果表明，钢轨和轨道板竖向加速度在冻胀起始点差值较大，而在冻胀其他位置二者比较接近。这说明冻胀起始位置的变形对无砟轨道结构竖向振动加速度影响比其他位置大。

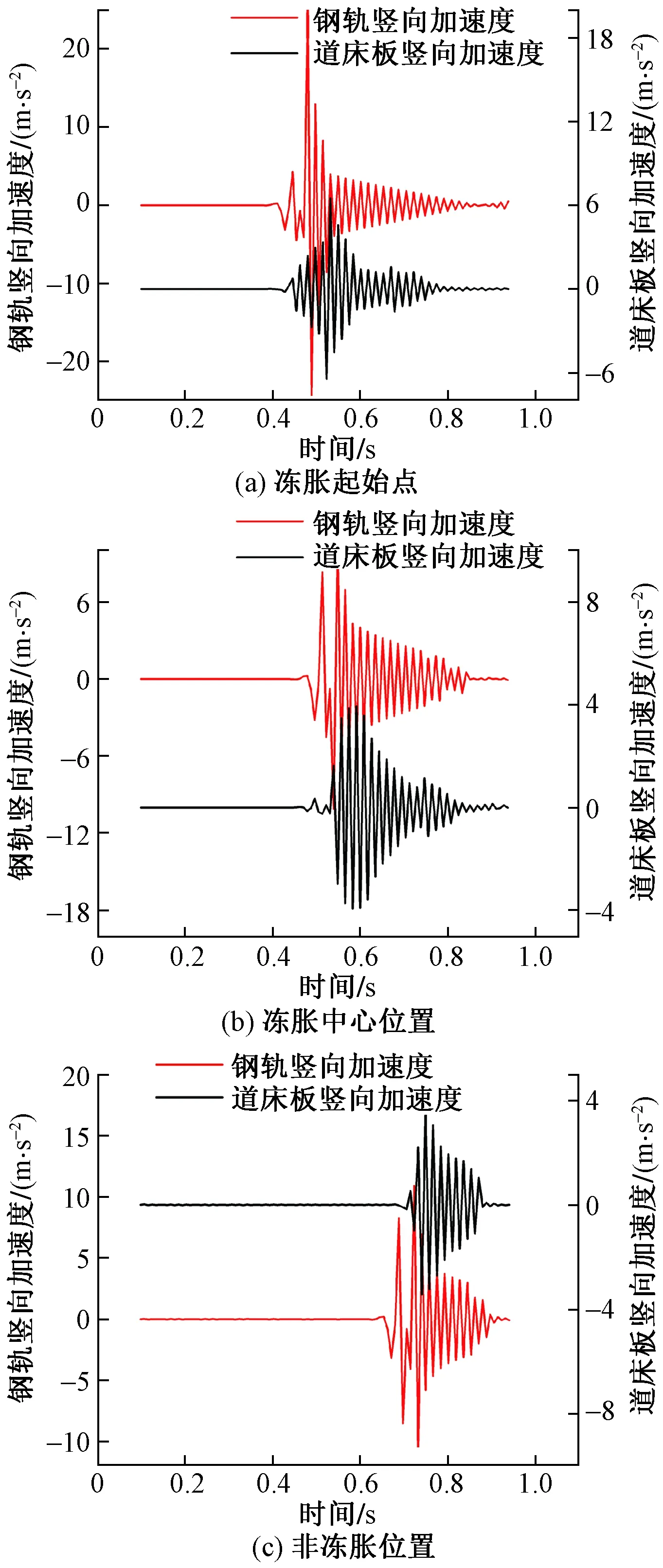
图4 不同位置处钢轨和道床板竖向加速度时程曲线Fig.4 Time history curve of vertical acceleration of rail and track bed slab at different positions

图5显示了在典型冻胀条件下，车轮通过3个不同位置时每个扣件反作用力的响应。结果表明，当车轮通过指定位置时，扣件的反作用力突然增大，并发生显著变化。数值结果表明，冻胀中心和非冻胀位置处最大扣件支反力相差很小，分别为20.57 kN和20.61 kN，而冻胀起始点最大达到 28.1 kN，是其他位置的1.4倍左右。由此可见，随着轮轨垂向力的增加，冻胀起始位置扣件反力响应将增大，更能反映出冻胀起始位置离缝现象比较严重。

图5 不同冻胀位置扣件支反力Fig.5 Fastener support reaction force at different frost heaving positions

2.2 不同冻胀波长对系统动力效应的影响

当列车以250 km/h速度运行时，路基冻胀峰值为10 mm，研究冻胀波长在5～35 m递增条件下的车辆和无砟轨道结构的动力响应情况。

2.2.1 不同冻胀波长下车辆动力响应特征

图6所示为最大轮轨垂向力、轮重减载率和竖向加速度随路基冻胀波长的变化。可以看出，轮轨垂向力和轮重减载率变化趋势相同，均随着路基冻胀波长的增大逐渐减小，并且在冻胀波长为5～25 m 范围内减小的速率相对较快，当冻胀波长大于25 m时，最大轮轨垂向力和轮重减载率都趋于稳定。车体竖向加速度并非在一个方向上变化，加速度值表现为先增大后减小，在冻胀波长15 m时达到峰值0.18 m/s2，之后路基冻胀段竖向振动加速度不断减小，随着冻胀波长范围增加行车舒适度逐渐提高。因此，为提高列车运行安全性，可以对冻胀波长小于25 mm的路基冻胀进行整治。同时，为保持列车的舒适性，对路基冻胀波长为10～15 mm冻害进行重点整治，这样既可以解决安全隐患又可以提高行车舒适度。

图6 不同冻胀波长下车辆动力响应Fig.6 Vehicle dynamic response under different frost heaving wavelengths

2.2.2 不同冻胀波长下无砟轨道结构动力响应特征

图7反映了不同冻胀波长对钢轨、道床板的最大动态位移和振动加速度的影响以及最大扣件支反力变化情况。从图7中发现，无砟轨道各结构动力响应变化趋势基本相同，即随着冻胀波长的增大，响应数值逐渐减小，最后达到稳定。

由图7(a)可看出，随着路基冻胀波长的增加，钢轨和道床板竖向位移均减小。波长在5～10 m时，竖向位移明显减小，而在冻胀波长大于20 m时，竖向位移变化平稳。这表明路基冻胀波长较小时，道床板和支承层之间可能产生离缝，导致道床板变形量稍大，而随着冻胀波长的增大，在列车驶入或驶离冻胀区域过程中，支承层与路基之间的离缝慢慢减小，两者之间接触状态良好，路基对无砟轨道具有良好的约束作用，钢轨和道床板之间相互作用效应减小，进而缩减了它们的最大竖向动态位移。

图7 不同冻胀波长下无砟轨道各结构的响应情况Fig.7 Response of ballastless track structures under different frost heaving wavelengths

图7(b)表明，路基冻胀波长在5～20 m范围内，道床板和钢轨的振动加速度与垂向位移变化趋势一样，随着波长的增加而迅速减小，这说明由于支承层与路基之间离缝随着冻胀波长增加开始变小，会导致轮轨变形程度减弱，从而影响着钢轨和道床板的振动加速度，且钢轨振动通过扣件传递到道床板，由于能量在传递过程中逐渐衰减，道床板的最大竖向加速度相对钢轨的小。对轨道结构而言，持续的振动加速度会加速轨道和道床板结构的疲劳损伤。因此，通过控制路基的冻胀波长范围，可以减小路基与支承层之间的间隙范围，进而减小钢轨和道床板的动力响应。

图7(c)表明，随着冻胀波长的增加，扣件的支反力减小，减小速度也在减慢。对于无砟轨道而言，扣件支反力的减小有利于延缓扣件中垫板的疲劳破坏。所以，加强对短波冻胀路基进行治理对于提高无砟轨道结构的损伤性能意义重大。

2.3 不同冻胀峰值对系统动力效应的影响

在分析路基不均匀冻胀变形下不同波长对轮轨系统振动响应影响基础上，研究路基冻胀波长 10 m时，冻胀峰值分别从5 mm递增至20 mm条件下的车辆和无砟轨道结构的动力响应情况。

图8 不同冻胀峰值下车辆动力响应Fig.8 Vehicle dynamic response under different frost heaving peaks

2.3.1 不同冻胀峰值下车辆动力响应特征

图8所示为最大轮轨垂向力、轮重减载率和竖向振动加速度受路基冻胀峰值变化的影响。从图8中可以看出，随着冻胀峰值的增大，轮轨垂向力、轮重减载率、车体最大竖向加速度均呈增长的趋势，但变化规律略有不同。

路基冻胀峰值对车体结构动力学影响与冻胀波长不同，在一定范围内，随着轮重减载率的增加，路基与支承层之间的间隙增大。当冻胀量大于 15 mm 时，最大轮轨垂向力和轮重减载率增长幅度开始变大，尤其在冻胀量为20 mm时，轮轨最大垂向力比较接近容许值，这说明冻胀峰值的不断增大对无砟轨道动力破坏具有潜在威胁。此外，随着冻胀峰值在5～20 mm增加时，竖向加速度的阶段性增加量分别为0.089、0.082、0.079 m/s2，可结果表明，垂直加速度的增长趋势具有良好的线性关系，反映了路基冻胀峰值对列车运行舒适性的明显影响。因此，对路基冻胀峰限值的控制能有效保证行车的安全性和舒适性。

2.3.2 不同冻胀峰值下无砟轨道结构动力响应特征

路基不同冻胀峰值条件下，钢轨、道床板的最大动态位移和振动加速度的影响以及最大扣件支反力变化情况，如图9所示。

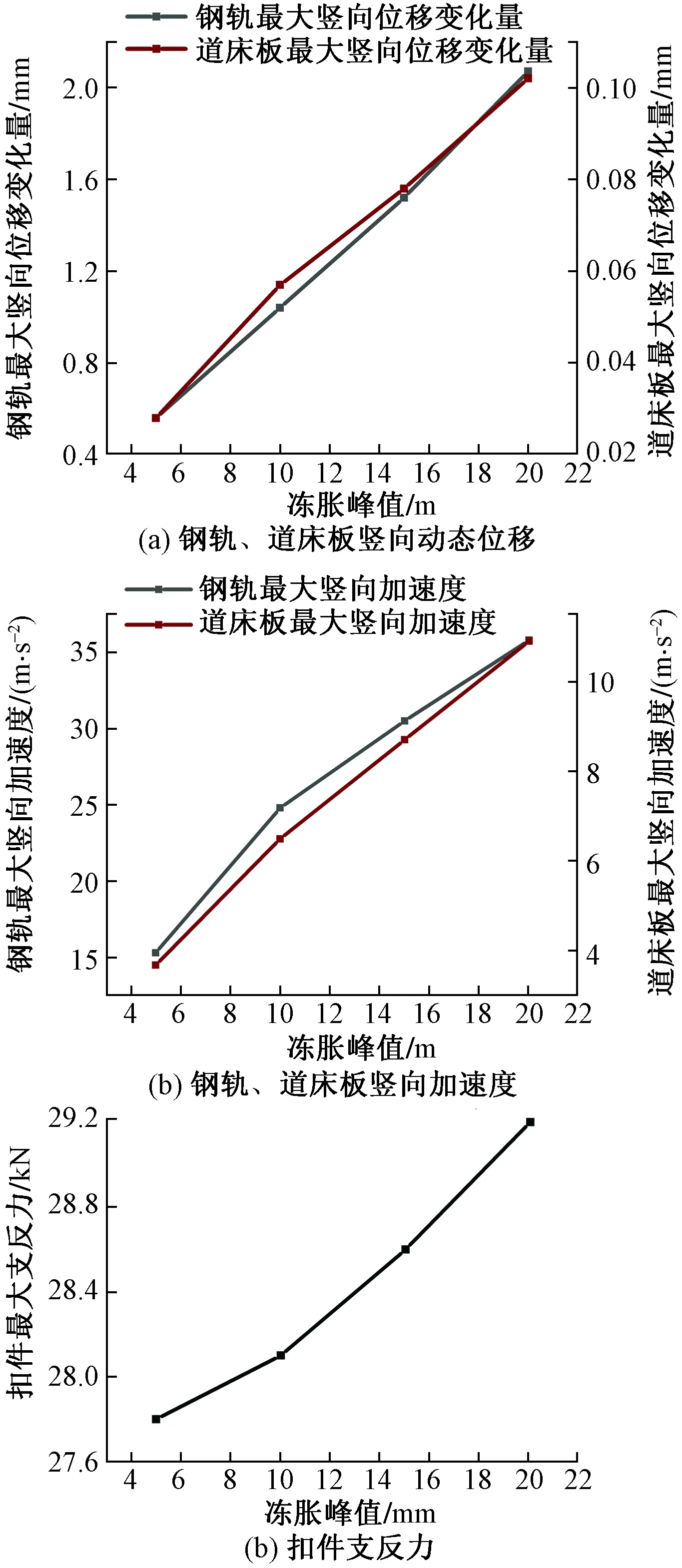
图9 不同冻胀峰值下无砟轨道各结构的响应情况Fig.9 Response of ballastless track structures under different frost heaving peaks

图9反映了不同冻胀变形峰值情况下无砟轨道各结构的动力响应。可以发现，钢轨、道床板以及扣件这3个主要结构物在列车驶入路基冻胀变形区域后，随着冻胀峰值的增加，其竖向位移量、振动加速度等显著增大。由图9(a)可知，自冻胀峰值从 5 mm 开始慢慢增大，路基与支承层之间离缝开始出现并逐渐扩大，导致无砟轨道整体变形范围增大，路基的支承作用随着峰值变化开始慢慢减弱，最终在车轮冲击作用下，道床板和钢轨竖向位移开始增大，尤其是钢轨的位移量呈现出明显的线性关系，当冻胀峰值继续增加时，有可能使得钢轨达到刚度极限，会给轨道结构带来极大的危害。图9(b)反映了钢轨和道床板的竖向振动加速度随着冻胀峰值的增大而增大，振动加速度影响着列车的舒适度，而冻胀峰值又对加速度的改变作用明显。冻胀峰值增大会引起轮轨相互作用力增大，进而引起钢轨和道床板的振动加速度的变化幅度增大，冻胀峰值20 mm时已达到35.8 m/s2，已经严重影响了行车的舒适度，有必要将路基高冻胀峰值产生的空隙减至最小，以提高轨道表面的几何平整度，达到行车平稳的效果。图9(c)反映了路基冻胀峰值的增大，扣件支反力也保持增长，但增长的幅度很小，冻胀峰值从5～20 mm，支反力仅增大了 1.4 kN，说明冻胀峰值的变化对扣件支反力的影响相对较小。

3 结论

(1)典型冻胀条件下，列车在进入冻胀变形区域后，车体加速度开始剧烈变化，冻胀起始和终止处车轮对钢轨的冲击较大，并且在冻胀中心附近车轮出现了明显减载，表明路基冻胀中心区域会对列车的运行安全性产生一定影响，因此，对车体而言，可适当减小驶入速度以降低风险；从无砟轨道结构在不同位置响应情况来看，可以发现钢轨和道床板在冻胀起始点出现较大离缝，易产生较大的不利响应，因此，关注冻胀起始位置是必要的。

(2)随着路基冻胀波长的增大，轮轨垂向力和轮重减载率最大值均逐渐减小。对冻胀波长小于25 m的路基冻胀进行整治，可以明显提高列车运行安全性，特别是波长10～15 m范围路基整治，对提高列车乘坐的舒适性有利。对于轨道结构而言，支承层与路基之间离缝较小时，钢轨和无砟轨道的响应值减小，因此，可以通过控制路基短波冻胀导致的脱空量，减小钢轨和道床板的动力响应。

(3)随着路基冻胀峰值的增大，轮轨在冻胀起始位置的冲击作用愈加明显，冻胀峰值为20 mm时，可能威胁到无砟轨道的结构性能；对于车体以及钢轨，竖向动态位移、竖向加速度和冻胀峰值之间保持近似线性关系，表明路基冻胀峰值对列车运行舒适度影响显著。因此，通过控制路基高冻胀峰值导致的脱空量，来减小钢轨和道床板的疲劳损伤是必要的。