基于耦合概率法的空间杆系结构失效概率分析

刘国光， 杨跃敏， 武志玮

(中国民航大学机场学院， 天津 300300)

空间杆系结构的可靠度水平可根据构件安全等级、失效模式和经济因素等综合确定，而结构失效分析是结构可靠性计算的重要内容[1]。通过量化评价不同失效模态对应的结构可靠性，可为结构设计、安装施工和结构安全使用提供重要依据。

结构可靠性研究的核心，是解决存在随机性条件下结构安全性的科学度量问题[2]。按照传统计算理论，概率分析的中心问题是极限状态的累积分布函数计算，不使用数值积分很难准确估计故障概率[3]。经典的一阶可靠性方法(first order reliability method,FORM)[4]和二阶可靠性方法(second order reliability method，SORM)[5]都是基于泰勒级数展开来建立极限状态函数的低阶近似方法[6]。近年来，蒙特卡罗法也作为一种经典的办法，常与其改进法进行对比[7]。李会军[8]讨论了空间网格结构失效过程中的可靠度与敏感度的关系，提出了材料非线性和初始缺陷对结构可靠度的影响。文献[9]为量化预测结构在不同失效模态下的失效概率区间，利用移除杆件法及结构应变能敏感度分析了空间杆系结构杆件群的鲁棒性。文献[10]基于结构刚度变化率对六角星型穹顶结构在阶跃荷载作用下的破坏过程进行了理论和实验研究。

结构失效具有一定的随机性，但又存在一定的区间变量。在结构可靠性界限理论中，二次二阶矩可靠性指标计算方法被普遍应用，利用位移插值函数及级数展开，对网壳结构提出合理的缺陷幅值来分析结构整体稳定性[11]。在此基础上，基于结构极限状态曲面的内包络面，进而通过计算包络面的失效概率确定结构的可靠性界限区间[12]。文献[13]推导了基于联合分布函数直接积分法的串联系统联合失效概率上限值计算公式，然而，目前国内外研究大多针对单阶和二阶失效概率，而对高阶耦合复杂空间杆件结构研究较少，涉及高阶失效时公式复杂，应用性较低。

为进一步研究多种失效模式下杆系结构的耦合失效概率来评价结构可靠度，完善结构失效的上、下界值，利用应力变化率法和杆件移除法相结合来评价单元杆件失效模态的相关系数，现通过间接积分法建立一种计算空间杆系结构耦合失效概率的新方法。并通过六角星型穹顶结构的模型破坏实验，结合泰勒展开法进行对比分析，总结耦合概率法在理论分析结果中的可靠性和先进性。

1 耦合概率法

三阶耦合概率法是基于所有单阶失效概率、所有二阶共失效概率和所有三阶共失效概率共同考虑，并在穷举组合得到失效概率基础上推导而来的。

1.1 杆件可靠性指标

为体现单元杆件的可靠性对结构整体可靠度的影响，引入β确定单元杆件可靠性指标。结构失效概率取决于其功能函数Z的分布形式，一般情况下，假定Z服从正态分布，即Z～N(μZ,σZ)。通过变换Y=(Z-μZ)/σZ,可将Z转换为标准的正态分布变量Y～N(0,1)。由数学概率密度函数和累积分布函数得

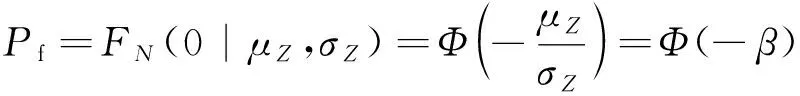
(1)

式(1)中：Pf为耦合失效概率函数；μZ为平均值；σZ为标准差。

由正态分布曲线可知，可以用σZ度量原点O到μZ的距离，因此将单元杆件的可靠性指标定义为无量纲数β，即

(2)

因此，结构失效概率可表示为

Pf=1-Φ(β)

(3)

1.2 杆件相关系数

当结构发生动力失稳时，总应变能发生突变，对应单元杆件的应变能会突然跳跃到一个相对较大值，而应力向量σ是一个有界向量。因此，如式(4)所示，当杆件应力变化率dσ突然跳跃到一个相对较大值时，由此可判定杆件发生动力失稳或多个杆件发生局部失稳[14]。

(4)

式(4)中：σi为第i个荷载步下的应力；σj为第j个荷载步下的应力，且i=j+Δt；Δt为应力采样周期。

将其与杆件移除法相结合，在移除某单元杆件后，分析剩余单元杆件受力过程中的应力变化率，再通过归一化可最终确定各单元重要性系数λi[15]。该方法是用于计算单元杆件重要性系数指标的高效、简便方法。

定义ρ12=ρ[M1,M2]是正态分布M1、M2的相关系数；λi定义为对应第i个失效模式的重要性系数，且ρij=λiλj，即耦合相关系数为

(5)

1.3 耦合失效概率

在复杂杆系结构中往往存在独立变量和相关变量，结构的功能函数可表示为

(6)

由于结构存在多子系统情况，失效极限状态满足正态空间分布后，原空间构成的极限失效概率曲面不再是单一的曲面，而是由两个边界面Pmaxg(β,λ)=0 和Pming(β,λ)=0构成的带状体，如图1所示。

图1 极限状态曲面边界Fig.1 Boundary of limit-state surfaces

直接求解空间混合子系统失效概率问题十分困难，近似地根据空间杆系结构受力特点和失效模态特征，假设空间杆系结构失效模态由n个失效模态(子系统)组成，将则杆系结构系统的失效事件可以表示为

E=E1∪E2∪…∪En

(7)

而系统失效事件E能分解为若干互斥事件，可表示为

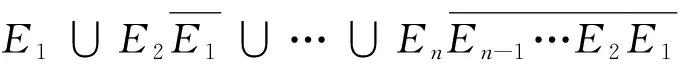
(8)

因为概率值为非负数，所以

(9)

成立，即系统耦合多阶失效的概率区间下界值。

另一方面，可得到系统多阶失效的概率区间上界值，计算式为

P(E)≤P(E1)+P(E2)-P(E1E2)+

(10)

用式(9)和式(10)即可获得各类参数已知的结构多阶耦合失效概率，包括单阶失效、二阶失效和三阶失效等。在假定结构失效符合正态分布的前提下，涉及二阶及以上失效计算时，都会出现二重、三重甚至更高阶积分形式。因此，通过间接积分法可将二阶失效概率和三阶失效概率转化为单次积分形式，表示为

(11)

式(11)中：φ(·)为关于β和λ的一阶失效函数。

(12)

结构系统的三阶耦合失效概率的上下界限可表示为

(13)

当阶数增加时，结构失效的上下界阈值宽度会减小，从而能够满足不同的可靠度精度要求。在工程结构可靠性分析中，点估计求解功能函数统计矩时建议求解至前三阶矩，改进后的依然可以用到第四阶矩，但是精度降低，然而，耦合概率在推广至四阶时，精度提高的同时会大大增加计算冗长，计算表明求解至三阶失效已经能够较高精度地确定结构的耦合失效概率。计算流程图如图2所示。

图2 结构失效概率计算流程图Fig.2 Flow chart of structural failure probability calculation

而泰勒展开依据矩估计法计算至四阶得到的四阶矩法的表达式[16]为

(14)

(15)

(16)

(17)

(18)

(19)

1.4 算例分析

假定某杆系结构由五种子系统组成，各子系统对应的独立变量(可靠性指标)和相关变量(重要性系数)如表1所示。

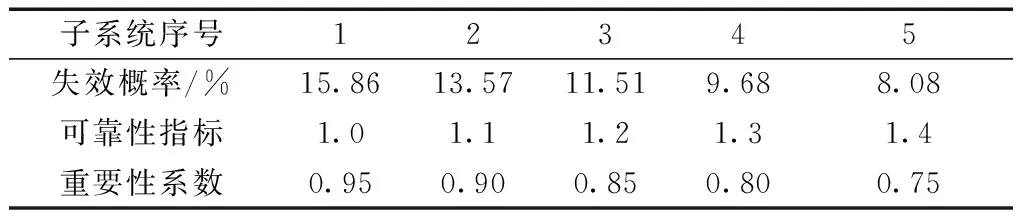
表1 子系统基本变量Table 1 Subsystem basic variables

通过式(11)可得二阶与一阶失效的关系如图3所示。

图3 二阶耦合失效概率对比Fig.3 Comparison of first-order and second-order coupling failure probability

通过式(12)可以计算得三阶失效概率为P123=0.060 173，P124=0.049 819，P134=0.042 495，P234=0.037 903，P125=0.040 608，P135=0.034 781，P145=0.029 202，P235=0.031 154，P245=0.026 327，P345=0.023 082。

根据式(13)计算结构耦合失效概率的上下界值为0.24≤Pf≤0.26。

结果表明，结构耦合失效概率区间为[0.24, 0.26]，而泰勒四阶展开失效概率区间为[0.228, 0.287]。从数值可以看出耦合失效概率下界值明显大于结构其他任何一阶、二阶、三阶失效的概率值。从二阶和三阶失效概率值可以看出，尤其在一阶失效概率较高的情况下，必须要考虑二阶和三阶的失效概率，如图3(a)～图3(c)所示。对比分析可以看出，泰勒展开法得出的结果对耦合概率法是包含关系，说明耦合概率法比泰勒展开精度更高。具体包含关系在下文实验中得到较好的验证。

2 结构模型实验

2.1 结构参数

如图4所示，模型实验结构为六角星型穹顶结构跨度2.6 m，由24根杆件组成，网架由6根0.3 m高的钢柱支撑，中心节点高为0.35 m，钢杆件弹性模量为206 GPa，泊松比为0.3。杆件均采用Q235等截面角钢∠25×3，截面面积为1.43 cm2，材料密度为7.58 g/cm3。如图5所示，杆件分为A、B、C三类，其中：杆1～杆6称为径向杆(A类)，杆7～杆12称为环向杆(B类)，杆13～杆24称为支座杆(C类)，杆件编号如图5所示。

图4 六角星型穹顶结构Fig.4 Hexagonal star dome structure

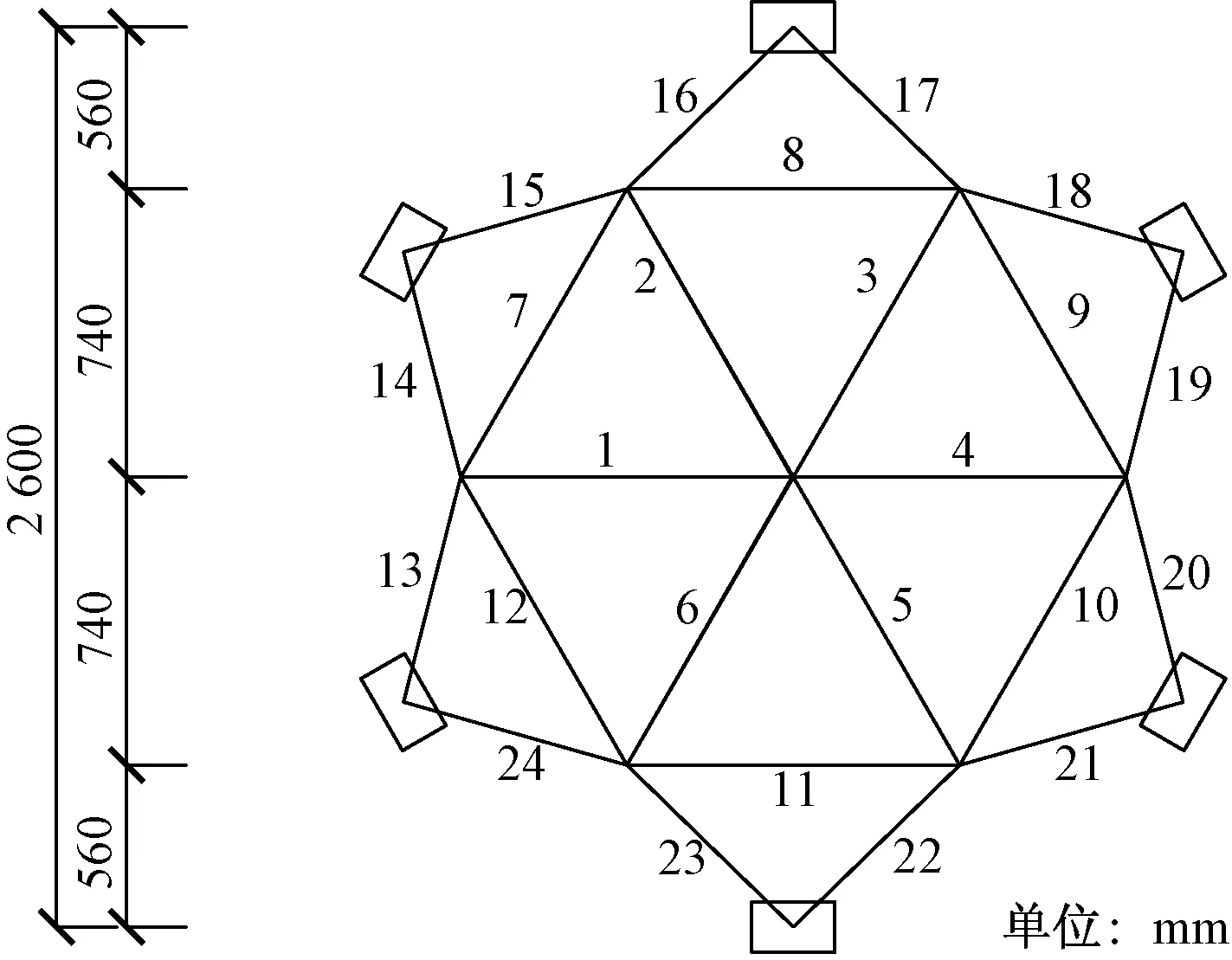
图5 六角星型穹顶结构平面图Fig.5 Plansheet of the hexagonal star dome structure

2.2 实验方法

基于六角星型穹顶结构对称性和各单元杆件受力特点，分别移除杆4(A类)、杆8(B类)和杆16(C类)。由于实验过程中各杆件处于弹性状态，可将应力变化作为研究结构整体可靠度的参考数值。因此，在杆1、杆2、杆9、杆11、杆20和杆21上贴应变片，记录实验过程的杆件应变变化。实验开始后在中央节点作用一竖向分步集中荷载，从0 s开始每隔15 s加载50 N,实验开始后连续加载至结构出现局部失稳或强度破坏为止，采样频率100 Hz。

3 实验结果及分析

3.1 原始结构的破坏模态分析

原始六角星型穹顶结构在阶跃荷载作用下的结构破坏过程中，将所测得的各应变片记录应变数值通过式(4)转化为杆件的应力变化率，所得曲线如图6所示。

图6 原始结构应力变化率Fig.6 Stress change rate of the original structure

在中心节点施加至675 N时，所有杆件均未出现应力大波动。因此外力在[0,675]范围内可视为结构处在线弹性范围内，杆件可靠性存在线性变化。为分析支座杆件可靠性指标对结构整体失效概率的影响，考虑在结构未超过使用年限的情况下，假设支座杆件可靠性指标从1.0取值至2.5，分别计算完整结构三阶耦合失效概率，如图7所示。

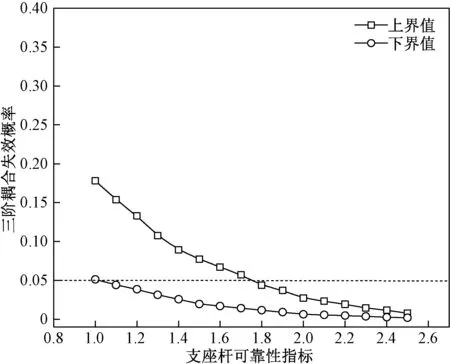
图7 原始结构三阶耦合失效曲线Fig.7 Third-order coupling failure curve of the original structure

当中心节点处荷载施加至700 N时，所有杆件单元的应力变化率均产生显著变化，其中支座杆20应力变化率最大，达到了1 520，径向杆2的应力变化率达到了723，此时结构中心径向杆发生跳跃失稳，其破坏模态如图8所示。

图8 原始结构破坏图Fig.8 Failure of the original structure

支座杆件在结构破坏瞬间承受了径向杆件群局部失效所引起的内力重分布，由于设计中支座杆件留有足够安全度，使得杆件可靠性指标较高，结构未发生连续倒塌破坏，也未发生多模态耦合的整体失效。

可见，对于实验所采用的六角星型穹顶结构，随着杆件可靠性指标增加，结构发生整体倒塌破坏的概率呈抛物线状下降。当支座杆件可靠性指标达到2.5时，结构整体失效概率低至1%，若按结构安全性95%来控制结构整体失效，将支座杆件可靠性指标控制在1.8时，结构经济性较好。

3.2 构件移除后分析

移除径向杆4后，在阶跃荷载作用下，结构破坏过程中各应变片记录的杆件应力变化率曲线如图9所示。

图9 移除杆4后结构应力变化率曲线Fig.9 Curve of structural stress change rate after removing rod 4

当中心节点处荷载施加至600 N时，各杆件单元的应力变化率随着下级荷载施加均产生显著变化，其中环向杆11应力变化率最大，达到了320，径向杆20的应力变化率达到了146。环向杆件在结构破坏瞬间主要承受了径向杆件群局部失效所引起的内力重分布。移除结构一根内径杆造成结构破坏的极限荷载由710 N降低到了630 N，降低幅度达到11.2%，受力整体性削弱严重，发生跳跃失稳，其破坏模态如图10所示，说明保证结构的完整性对结构的安全性至关重要。

图10 移除杆4后结构破坏图Fig.10 Structural damage after removing rod 4

但是，结构仍具有较高的可靠性指标，未发生整体破坏。但结构发生整体破坏的可能性依然存在，其三阶耦合概率法与泰勒展开法上下界限值随荷载步的变化情况如图11所示。

图11 移除杆4后结构三阶耦合失效曲线Fig.11 Comparison of structural failure curves after removing rod 4

在阶跃荷载下，两种方法失效概率趋势相同，相比之下，耦合概率法得出的失效概率阈值更小，耦合概率法完全置于泰勒展开法所求的失效带中。由于实验在分步荷载下进行，结构的失效应力变化出现跳跃现象，但是从失效概率趋势图中能够在下级荷载造成的应力突变前获得失效概率激增，当荷载施加至550 N时，失效概率均表现出激增态势，因此，可实现在不破坏结构形态的前提下，预测结构的承载能力。

同理可得在结构分别移除环向杆和支座杆件后的结构应力变化图，如图12、图13所示。

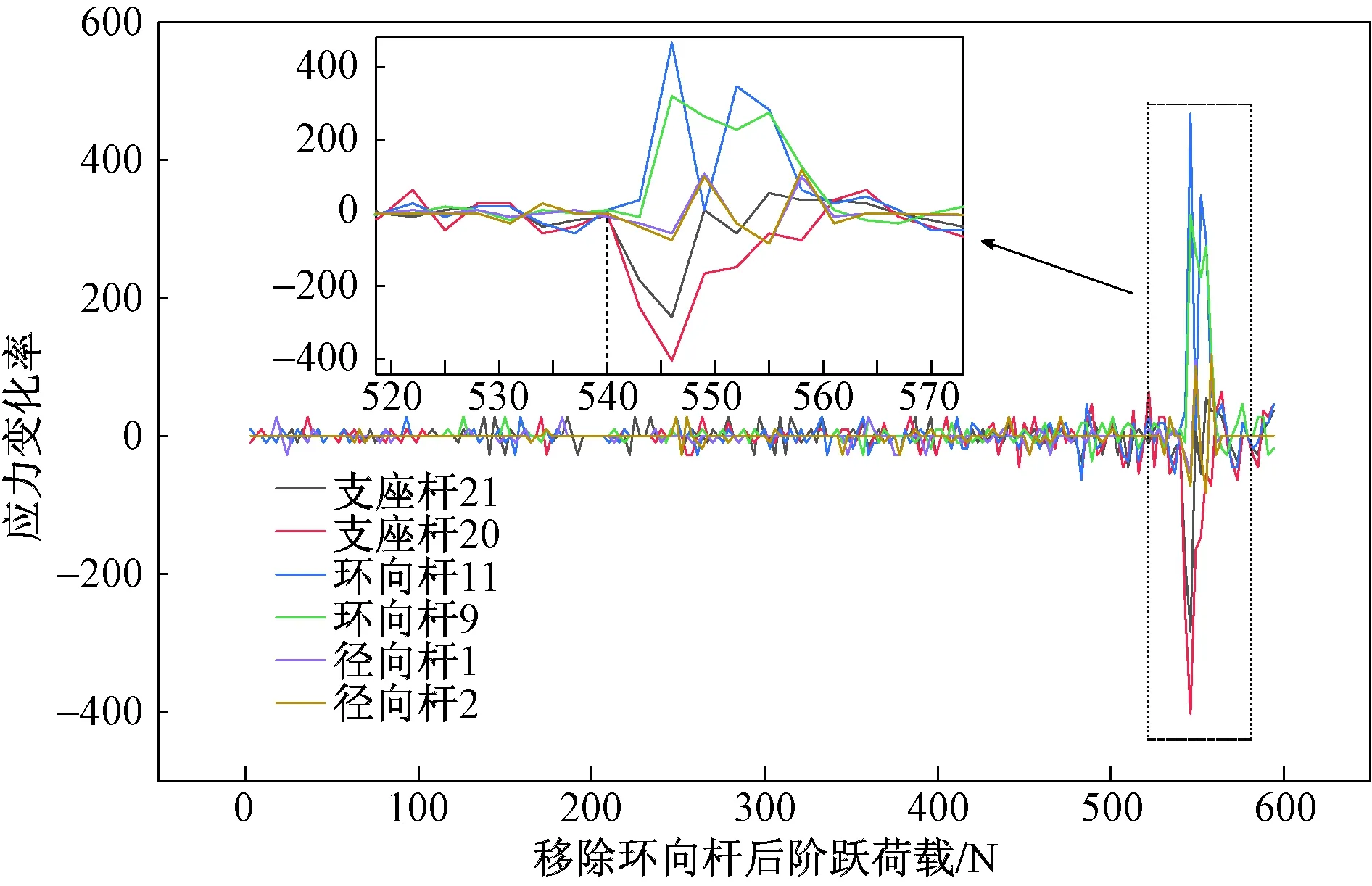
图12 移除杆8后结构应力变化率曲线Fig.12 Curve of structural stress change rate after removing rod 8

图13 移除杆16后结构应力变化率曲线Fig.13 Curve of structural stress change rate after removing rod 16

从图12可以看出，当中心节点处荷载施加至540 N时，结构各杆件发生剧烈应力变化，其中环向杆11应力变化率最大，达到了467，支座杆20的应力变化率达到了422，计算可得，结构整体可靠性下降20%，此时结构中心径向杆发生跳跃失稳。从应力变化图中也可看出，部分环向杆发生了应力拉压变换，从而实现内力的重分布，发生局部失稳后，还能维持结构整体稳定性。

图14 移除杆8、16后结构三阶耦合失效曲线Fig.14 The third-order coupling failure curve of the structure after removing the rods 8 and 16

对比前三次实验的应力变化率曲线，观察图13(b)(中心节点处荷载施加300～460 N)可知，各杆件单元的应力变化率出现不稳定变化。从实验现象可知，随荷载增加持续变大，在达到最大值后未发生结构破坏，而是持续跳跃平衡。当结构进入阶段2后，应力出现剧烈变化，荷载接近550 N时，结构耦合失效概率的上下界值区间为[0.26, 0.33]。如图14所示，随后失效概率激增，结构发生整体倒塌。对比其他杆件移除后的结构失效概率，表明支座杆对结构耦合失效概率影响最大，结构由单阶失效模态控制(局部压杆的跳跃失稳)转变为多阶失效模态控制(整体倒塌)，耦合失效概率的理论计算结果同结构模型实验现象一致。

4 结论

通过应力变化率法和杆件移除法计算杆系结构单元杆件失效模态的相关系数，初步建立了一种可计算杆系结构失效概率、预测杆系结构失效模态和量化评价结构可靠度的耦合概率法。利用该方法，可获得不同结构失效模态对应的失效概率区间，进而通过量化比较预测结构可靠性及对应的失效模态。

(1)利用单元杆件的应力变化率，对结构施加相应的荷载步，在单元杆件应力变化率发生突变的同时，结构的三阶耦合失效概率也发生了突变，验证了耦合失效概率法的准确性。

(2)六角星型穹顶结构模型破坏性实验现象表现为：移除径向杆及环向杆后，结构失效模态为跳跃失稳；移除支座杆件后，结构失效模态为整体失稳。结果表明，支座杆件决定着结构的整体稳定性。当降低支座杆件设计安全裕度时，结构发生整体失效的概率显著上升。此概率值可作为量化评价结构安全性和结构经济性的指标。对本结构模型，支座杆件可靠性指标为1.8时，可达到可靠度95%的经济最优化设计目标。

(3)通过耦合概率法量化计算不同荷载步下结构的三阶耦合失效概率可知，结构发生整体失效的概率随荷载步增加不断变大，在结构破坏前失效概率会出现激增。该结论可为空间杆系结构施工及使用阶段的健康监测提供新的技术方案。