一种在网格内部捕捉间断的Walsh 函数有限体积方法1)

任炯 王刚

(西北工业大学航空学院,西安 710072)

引言

在计算流体力学(computational fluid dynamics,CFD)领域中,对超声速或高超声速流场进行数值模拟时,经常会出现激波或剪切层(接触面)等较为复杂的间断流场结构.对于这些间断结构,往往需要采用特殊的数值算法处理才能得到满足精度或分辨率需求的模拟结果.目前通用的间断处理方法主要有两类:激波装配法[1-6]和激波捕捉法[6-12].

激波装配法的基本思想是:将激波作为流场区域里的运动边界进行处理,利用Rankine Hugoniot(RH)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点,缺点是算法复杂,尤其是流场中激波相互干扰作用,演化形成多尺度激波的复杂结构时,一般需要采用动网格技术才能完成[6]计算.而基于有限体积[6]或有限元[13-14]的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理,只需假设激波间断位于流场网格离散后的控制体交界面处,根据交界面两侧的流场状态量近似求解Riemann 问题,便可自动模拟出激波的位置和强度.近似求解Riemann 问题时通常采用的方法有通量矢量分裂格式[15-17]或通量差分分裂格式[18-22].相对于激波装配方法,基于有限体积[6]或有限元[13-14]的激波捕捉方法算法简单,而且可以在流场的光滑区域和间断区域采用统一的格式计算,大大提高了计算效率.另外,该类方法还具有良好的几何外形适应性.目前,它们已经发展成为CFD 领域中有效且主流的间断数值模拟技术之一.然而,要达到与激波装配方法相同的流场模拟精度和分辨率,其必须使用巨大的网格量或采用高阶的流场重构技术[23-33].

通常,“间断位于控制体交界面处”的假设使激波捕捉方法所引入的激波描述误差较大,尤其在质量较差的粗网格上更为明显,一般表现出锯齿状的激波面.为了突破以上假设的限制,能够在“控制体内部捕捉到激波”的算法研究已经成为目前CFD 技术发展的目标之一.

国际上,已有一些学者进行了相关的研究,如Persson 和Peraire[34]在高阶间断Galerkin(discontinuous Galerkin,DG)方法的背景下,通过给原始控制方程增加人工黏性项将激波(间断)尺度拉伸,使得可以利用高阶连续近似的方法模拟黏性激波中包含的大梯度区域.他们的研究发现,p阶多项式的连续近似只需要O(h/p)(h为网格尺度)的黏性就能分辨出激波,得到比控制体单元尺度更小的激波结构,由此达到子单元尺度分辨率的激波捕捉效果(即在控制体内捕捉激波的分辨率).不过该方法在引入数值或物理黏性模型的同时会增加需要经验调节的参数,且对于不同的计算问题需要不同的黏性模型才能得到稳定的结果.此外,该方法只有在近似多项式的阶次很高(≥8 阶)时,才具有网格内部的间断捕捉能力,对于简单的常数/线性近似,其结果甚至不及原始方法的分辨率.

美国学者Gnoffo[35-36]将一组具有正交性的间断Walsh 基函数[37-38]引入到CFD 领域,利用Walsh 基函数求解具有间断解的非线性微分方程[35].其基本方法是根据Walsh 基函数的乘法封闭性和一些基本变换算子(如倒数变换、积分变换、微分变换等)将原始的微分方程变换到波数空间的多项式方程系统,在波数空间上求解原微分方程的全局解,以期得到比传统有限体积方法更好的间断捕捉效果.然而,在求解一维Burgers 方程和Euler 方程的算例中,该方法并没有达到预期的理想效果.主要表现在两个方面:其一是求解非线性偏微分方程时,各个原始变量的Walsh 基函数级数近似会引入很多复杂的多重交叉相乘项,导致最终得到的代数方程系统过于复杂,且边界条件的处理也比较困难;其二是该全局解方法完全脱离了有限体积离散的框架,没有明确的网格划分过程,只针对最终的代数方程系统进行数值迭代求解,且采用数百个Walsh 基函数得到的数值结果与传统采用迎风格式的有限体积方法的结果相比,也并未表现出明显的优势.

针对Persson 和Peraire[34]与Gnoffo[35]所提出的方法中存在的问题,本文提出了一种新型有限体积方法,该方法在保持有限体积离散优势的基础上,充分利用了Walsh 基函数的间断特点,且能达到以下两点目的:(1)避免Gnoffo[35]所提出的全局解方法的复杂性和数值模拟的局限性;(2)仅采用低阶近似(如常数近似或线性近似)便可在网格内部捕捉到激波间断,达到子单元尺度的激波分辨率.本文方法的基本原理是:摒弃传统有限体积和有限元方法中流场变量在网格内部连续的假设,将守恒变量表示为截断Walsh 基函数的级数形式.借助Walsh 基函数本身所具有的间断方波属性,在控制体内部配置间断.所配置的间断自然地将控制体虚分成若干个连续的子单元,将得到的关于Walsh 基函数级数的守恒型控制方程系统在这些子单元上积分离散,得到了一种新的求解方法.该方法对变量的基函数表示与有限元思想类似,且最终得到的离散系统也与有限元方法相似.但在子单元上的积分并没有变分过程,而与有限体积方法完全相同.因此该方法虽然在思想上介于有限元和有限体积方法之间,但本质上属于有限体积的离散框架.本文称该方法为“Walsh 函数的有限体积方法(finite volume method with Walsh basis functions,FVM-WBF)”.仅依赖Walsh 基函数组离散的FVM-WBF 方法在子单元尺度上只有1 阶计算精度.为了进一步提高对光滑解的分辨率,采用子单元上的流场变量均值进行流场的线性重构,将FVMWBF 方法的离散精度提升到2 阶.在数值算例部分,运用1 阶和2 阶FVM-WBF 方法求解了无黏Burgers方程和Euler 方程的多个定解问题,以期验证FVMWBF 方法的计算精度、计算效率、激波捕捉能力和鲁棒性.

1 Walsh 基函数

Walsh 基函数由一类具有间断特点的分段常数函数构成.在给定区域上,每个Walsh 基函数的图像都由若干个相等幅度的方波构成.

若采用gn(x)表示闭区间[xa,xb]上具有n个波段的Walsh 基函数,则有如下计算公式[35]

其中

则称gn(x)属于p组.一般gn(x)的最小波段长度定义为

且p组Walsh 基函数的波段长度最多包含两种,即dxp或2dxp.因此式(2)中(i)的取值为1 或2.另外,Walsh 基函数还具有正交性等优良数学特征,详细描述可参考文献[35],此处不赘述.

图1 展示的是前4 组(0≤p≤3)Walsh 基函数(g1(x)∼g8(x))的函数图像,可以看到,各函数均由若干个等幅方波构成.

图1 闭区间0≤x≤1 上, p=0,1,2 和3 组的Walsh 函数示意图: g1(x)∼g8(x)Fig.1 Walsh functions for p=0,1,2 and 3 in the interval 0≤x≤1: g1(x)∼g8(x)

Gnoffo[35]通过研究Walsh 基函数级数对若干连续和间断函数的拟合特点提出了求解非线性偏微分方程的Walsh 基函数全局解方法.该方法采用时空耦合算法,将微分方程的各变量表示成关于时间和空间的二元Walsh 基函数级数形式,并直接对微分方程做Walsh 基函数级数的积分或微分变换处理,最终得到关于基函数系数的复杂非线性代数方程系统,需要通过Newton 迭代[35]等数值手段才能完成计算.虽然Walsh 基函数全局解方法思路简单,但存在一定的局限性,如:(1)求解不同的微分方程需要重新推导代数方程组,因此不具有普适性;(2)当微分方程的初边值条件复杂时,其基函数级数展开可能导致最终的代数方程系统求解时收敛困难;(3)文献[35]的测试算例显示要得到与传统有限体积方法类似的模拟效果,微分方程变量的每个维度采用的基函数个数一般要达到28量级左右,这将会给最终非线性代数方程系统的求解带来较高的计算量负担.

受Gnoffo[35]研究的启发,本文将具有间断特性的Walsh 基函数与传统有限体积方法结合,提出了新的FVM-WBF 方法,以期在一定程度上改善Walsh 基函数全局解方法的局限性.

2 FVM-WBF 方法

根据Walsh 基函数级数对任意函数拟合的合理性[35],本文考虑采用截断Walsh 基函数级数近似双曲守恒律方程中的守恒变量,下面针对一维和二维情况分别进行讨论.

2.1 一维FVM-WBF 方法

为描述简便,我们先以标量守恒律方程为例

其中u=u(x,t)为守恒变量,f(u)=f(u(x,t))为通量函数.若采用传统有限体积方法对守恒方程(5)进行离散,需将其在给定控制体Ωi上进行积分,并假设控制体单元内的守恒变量为连续分布函数,从而得到关于守恒变量单元平均值的半离散方程

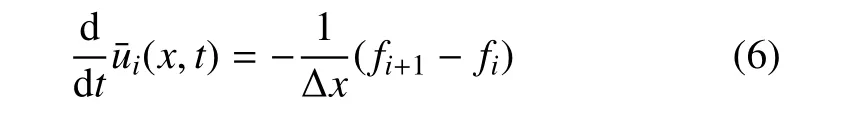
现对守恒变量u进行截断Walsh 基函数级数近似如下

式中ck(t)是随时间变化的Walsh 基函数系数,且n=2p(p=0,1,2,···).将式(7)代入式(5),则得到关于系数组和Walsh 基函数组的守恒型方程组

图2 控制体Ωi 内的变量分布示意图Fig.2 Variable distribution in the control volume Ωi

经整理,该式可写成

根据式(7),不难发现n(n=2p,p=0,1,2,···)个Walsh 基函数的级数表达形式将会给控制体Ωi内的守恒变量近似分布中均匀引入n−1 个间断.若取n=4,那么控制体Ωi内的3 个间断位置如图2 中的灰色竖直虚线所示.沿着n−1 个间断所在位置进行划分,控制体Ωi将被均匀地分割为n个大小相同的子单元,用Ωi,j(j=1,2,···,n)表示.对于一维情况,Ωi,j=[xi,j−1,xi,j],将关于Walsh 基函数系数组的守恒型方程(9)在子单元Ωi,j上积分,有

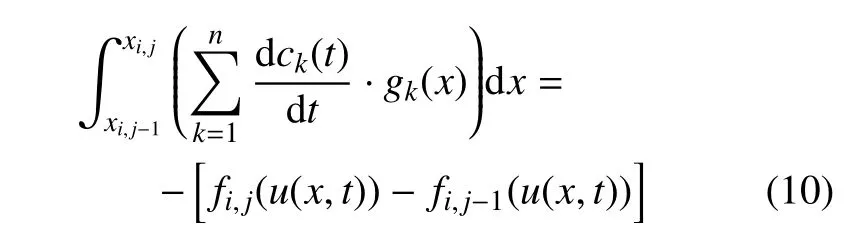
若定义子单元积分平均为

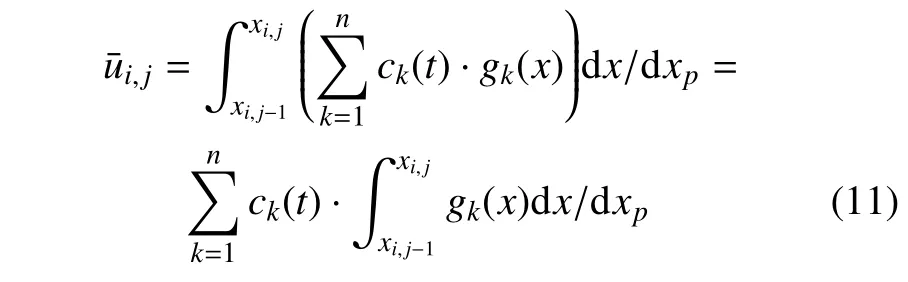
其中dxp=xi,j−xi,j−1,则方程(10)可写为如下半离散形式

另外,由式(7)还可知子单元内守恒变量为常数分布近似,所以在整个控制体Ωi内,守恒变量的分布具有分段常数的特点,如图2(c)所示.

根据式(11),对方程(10)进一步整理,可得到方程(12)的矢量形式

若将守恒型方程(9)在所有子单元上积分离散,则可在控制体Ωi上得到关于Walsh 基函数系数矢量C的紧致矩阵方程

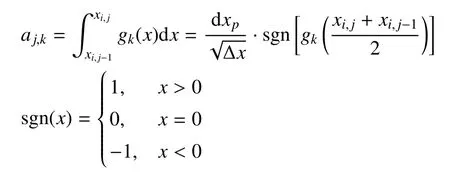
该矩阵中元素的计算公式为矩阵A(n)表示n个Walsh 基函数对应得到的矩阵,其中所有元素的公因子为,所以该矩阵可归一化为只包含±1 的常数矩阵.例如,当n=2,4,8 时有

显然,矩阵A(n)对称可逆,因此方程(15)的“解的存在性”得到保证.一个有趣的特点是矩阵A(n)的逆A(n)−1可由A(n)直接计算得到,即

根据该特性,在求解时可以省略矩阵求逆的过程,直接由预先储存的A(n)进行计算,这在一定程度上对计算效率是有益的.

以上介绍的求解标量方程的FVM-WBF 方法同样适用于求解守恒型方程系统,例如,对于一维Euler方程

其中ρ,u,p,E分别为密度、速度、压强和单位体积总能,m=ρu,状态方程为

γ=1.4 为理想气体常数.

类似于标量情况,对3 个守恒变量(密度ρ,动量m和能量E)进行截断Walsh 基函数级数近似

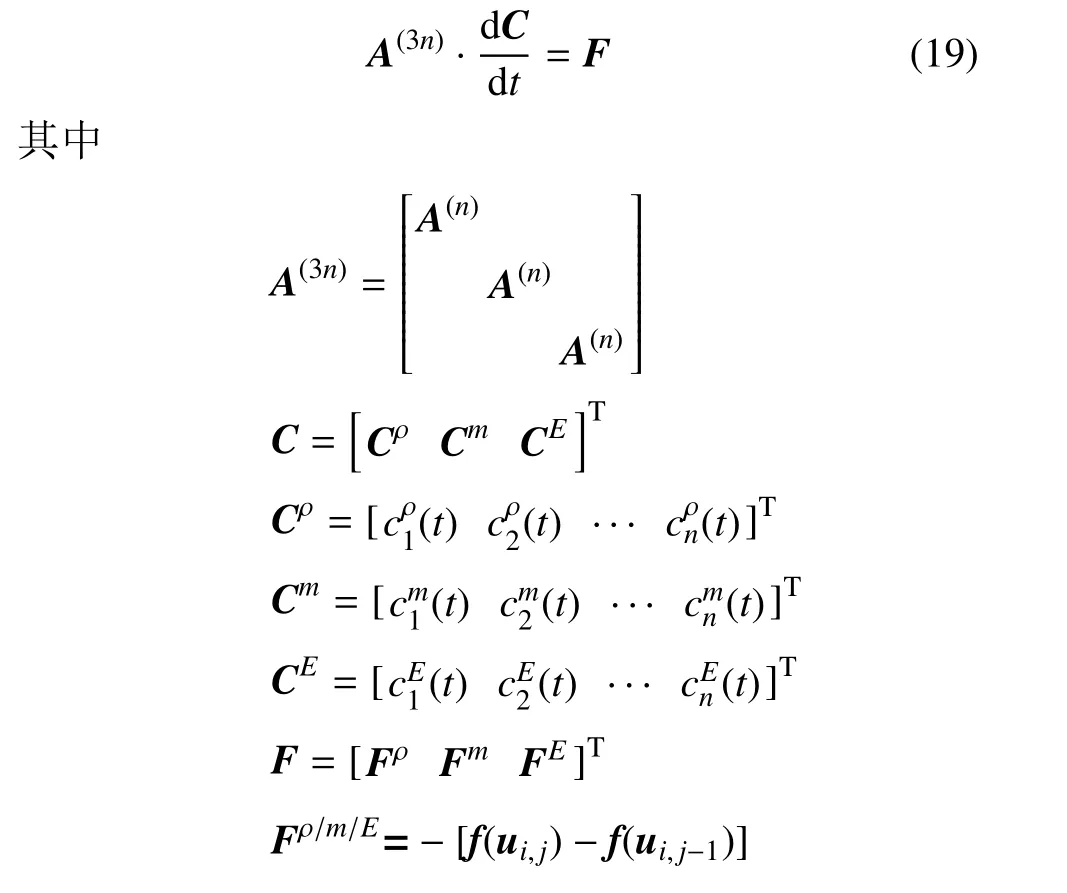
2.2 二维FVM-WBF 方法

对于二维情况,同样先考虑标量守恒律方程

其中u=u(x,y,t)是守恒变量,f(u)和g(u)分别是x和y方向上的通量函数,(x,y)∈Ω(Ω 为求解域).

在控制体Ωi上,对守恒变量u=u(x,y,t)进行如下Walsh 基函数级数近似

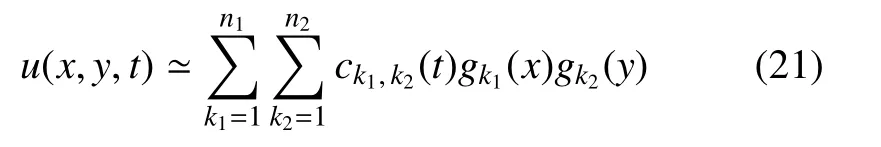
其中,n1和n2分别为x和y方向上各自使用的Walsh基函数个数,ck1,k2(t)表示对应的基函数系数.

显然,在控制体Ωi内,式(21)会给守恒变量的近似分布函数中引入n1+n2−2 个间断(其中x方向为n1−1 个间断,y方向为n2−1 个间断).沿着间断,可将原始控制体Ωi分割为n1·n2个大小完全相同的子单元,同样用Ωi,j(j=1,2,···,n1·n2)表示.与一维方法类似,将式(21)代入守恒型方程(20)后,在每个子单元上进行积分离散.最终得到关于Walsh 基函数系数组

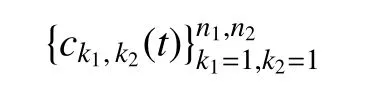
的紧致型矩阵方程

其中C=[c1,1(t)···c1,n2(t)c2,1(t)···cn1,n2(t)]T,F=[Fi,1Fi,2···Fi,n1·n2]T,(Fi,j(j=1,2,···,n1·n2)为Ωi,j上x方向的通量),G=[Gi,1Gi,2···Gi,n1·n2]T,(Gi,j(j=1,2,···,n1·n2)为Ωi,j上y方向的通量).对于二维情况,矩阵A(n1,n2)可由相应的2 个一维矩阵的张量积得到,即A(n1,n2)=A(n1)⊗A(n2)(⊗表示张量积),也可由相应的元素公式计算得到

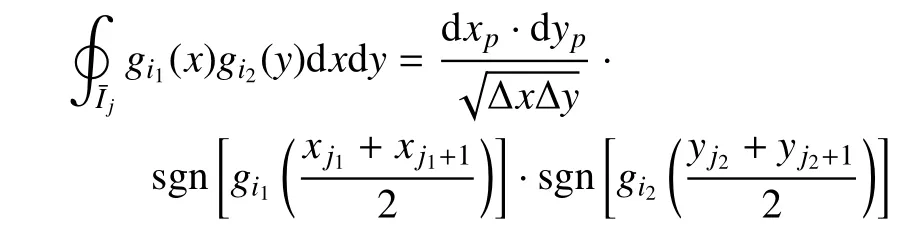
该矩阵同样对称可逆,所以对于方程(22),“解的存在性”可以得到保证.而且A(n1,n2)的逆也可由其本身计算得到,即

(p1和p2分别是n1和n2对应的Walsh 基函数组数)或者由对应的两个一维逆矩阵的张量积得到,即

实际求解时,矩阵A(n1,n2)及其逆都可预先计算并储存,以减少计算过程中矩阵求逆带来的计算量.

对于二维守恒型方程系统,将守恒变量按分量进行Walsh 基函数级数近似,可得到与方程(19)类似的块对角紧致矩阵方程,对角线上的每个矩阵均为A(n1,n2),其推导过程类似一维情况,这里不再赘述.

由上述描述可知,FVM-WBF 方法采用时空分离的思想在子单元框架下对微分方程进行有限体积离散,具有更好的普适性.且FVM-WBF 方法是根据Walsh 基函数引入的间断位置对原始控制体单元进行虚子单元划分,并不改变原始网格的几何拓扑结构,保持了原始网格良好的几何适应性.另外,对于边界条件的处理,FVM-WBF 方法与原始有限体积方法类似,为了保持与内场一致的数值通量计算,可以在边界处延拓一层辅助网格单元,用与边界单元相同的Walsh 基函数表达辅助网格上的流场变量,可以在边界处达到子单元尺度的误差精度.相对于Gnoffo[35]提出的Walsh 基函数全局解方法,FVM-WBF 方法并未在离散和求解方面引入新的困难.

2.3 误差和精度分析

传统有限体积方法假设控制体内的守恒变量为常数函数分布,如图2(a)所示.那么相对于每个控制体Ωi的尺度,计算精度为1 阶,其误差为O(∆x),即

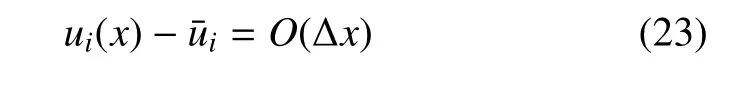
而对于FVM-WBF 方法,守恒变量采用Walsh 基函数级数近似(如式(7)),控制体内守恒变量的分布为分段常数函数形式(见图2(c)).相对于每个子单元Ωi,j的尺度,计算精度也为1 阶,子单元上的误差为O(dxi,p),即

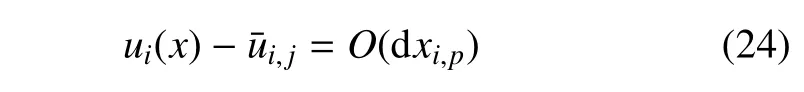
而对于整个控制体Ωi的尺度,Walsh 基函数级数近似的积分平均如下

当n=2 时,

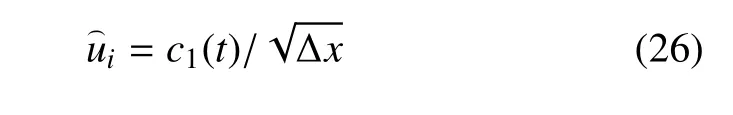
由子单元积分平均式(11),有

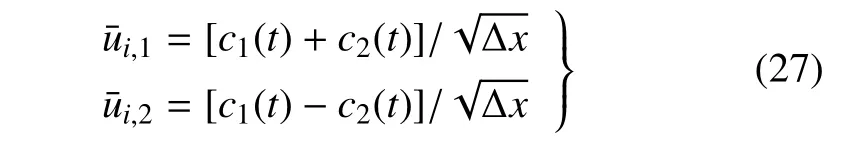
再由式(26)和式(27),可得

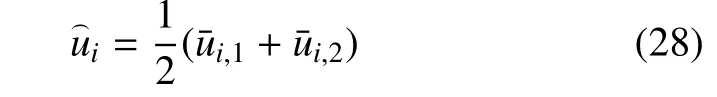
所以

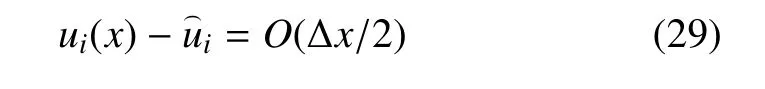
同理,

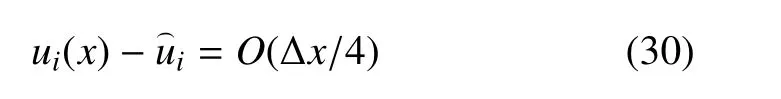
当n=4 时,有

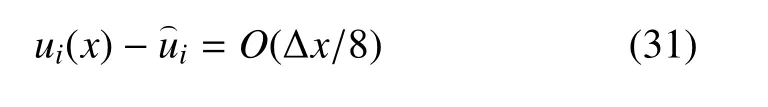
当n=8 时,有从以上推导可知,对于FVM-WBF 方法,当采用n=2p(p≥1)个Walsh 基函数对守恒变量近似时,其近似误差为O(∆x/2p).因此理论上,相对于传统有限体积方法,FVM-WBF (n=2p)方法的误差约以因子1/2p缩减,而收敛精度并没有提高.

通常,为提高精度,传统有限体积方法是在当前控制体和周围多个控制体构成的模板上,采用守恒变量均值进行多项式重构,如线性重构后,变量的分布如图2(b)所示.而本文根据FVM-WBF 方法的特点,采用控制体内的子单元均值(如式(11))进行线性重构实现2 阶精度的计算,具体公式如下

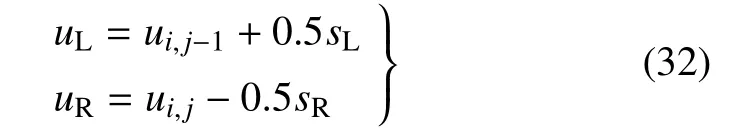
其中

线性重构后,控制体Ωi内的变量分布如图2(d)所示,为分段线性分布.传统2 阶有限体积方法与本文重构的2 阶FVM-WBF 方法在计算精度和计算效率方面的比较将在下小节的数值测试中进行讨论.

3 数值测试

本节采用FVM-WBF 方法对一/二维无黏Burgers方程和Euler 方程的几个非定常问题进行求解,并通过与传统有限体积方法的数值结果进行对比,测试和验证该方法的计算精度、计算效率、激波捕捉能力和鲁棒性.其中数值通量的计算均采用熵相容格式[21-22],时间推进均采用满足TVD 条件的3 阶显式Runge-Kutta[39]方法.

为便于表述,算例中采用记号FVM-WBF-O 表示初始没有线性重构的1 阶FVM-WBF 方法的数值结果,而用FVM-WBF-R2 表示经线性重构实现的2 阶FVM-WBF 方法的数值结果,作为对照,记号OFVM-1st 和OFVM-2nd 分别用来表示传统有限体积方法(用OFVM 方法表示)的1 阶和2 阶计算结果.一维算例中的Exact 表示解析解.

3.1 一维无黏Burgers 方程连续初值问题

Burgers 方程的第 1 个测试算例是一维区域[−2,2]上的连续初值问题,主要用以测试FVM-WBF方法的计算精度和计算效率,其初始条件为

解析解为

取u0=0,u1=0.5,采用周期边界条件.针对t=0.32和t=0.96 这两个时刻,分别在表1 到表4 中给出了不同网格上的OFVM 和FVM-WBF (n=2,4,8)方法1 阶与2 阶数值计算的L1误差与相应的收敛精度.可以发现,对于两种计算精度,OFVM 与FVMWBF 方法在两个时间点的收敛精度基本相同,但在相同网格上,相对于OFVM 方法,FVM-WBF 方法的误差约以因子1/2p缩减(这与第2.3 节分析的结论一致).若OFVM 方法采用的网格单元数目等于FVMWBF 方法的网格单元数与基函数个数的乘积时,在整个计算域上两种方法具有相同的自由度.对比表1 ∼表4 中两种方法自由度相同时的误差,可以发现,1 阶精度时两种方法的误差几乎相同,这说明FVM-WBF 方法表现出了与OFVM 方法网格加密等价的误差效应.而2 阶精度时,FVM-WBF 比OFVM方法的误差略小,这可能是由于子单元重构模板与原始控制体重构模板的差异造成的.另外,表2 和表4 给出的t=0.96 时刻的误差和收敛精度相对于t=0.32 时刻都有所减小,这是因为t=0.96 时刻在x=0位置处形成的压缩激波对精度造成了影响.图3(a)和图3(b)分别给出了网格量为M=20 时,两个时间点上两种方法的2 阶精度结果与精确解的对比,可以看到FVM-WBF 方法取n=2,4,8,3 种基函数级数近似时,在光滑解的极值附近和间断解处都表现出比OFVM 方法更好的分辨率.图3(c)展示的是两种方法取相同的自由度时(本算例的自由度为1280),其误差精度与所消耗的CPU 时间之间的关系,通过比较发现,当误差和收敛精度相同时,FVM-WBF 方法所消耗的CPU 时间都比OFVM 方法短,且随着Walsh 基函数数目的增大,FVM-WBF 方法的计算效率也逐步提高.

表1 OFVM 方法与FVM-WBF-O 的L1 误差和收敛精度(t=0.32)Table 1 L1-error and L1-order of OFVM and FVM-WBF-O method for t=0.32

表2 OFVM 方法与FVM-WBF-O 的L1 误差和收敛精度(t=0.96)Table 2 L1-error and L1-order of OFVM and FVM-WBF-O method for t=0.96

表3 OFVM-2nd 方法与FVM-WBF-R2 的L1 误差和收敛精度(t=0.32)Table 3 L1-error andL1-order of OFVM-2nd and FVM-WBF-R2 method for t=0.32

表4 OFVM-2nd 方法与FVM-WBF-R2 的L1 误差和收敛精度(t=0.96)Table 4 L1-error and L1-order of OFVM-2nd and FVM-WBF-R2 method for t=0.96

3.2 一维Euler 方程激波管问题

本算例求解了一维Euler 方程的两种激波管问题(SOD 激波管和LAX 激波管).在相同网格上比较了FVM-WBF 方法和OFVM 方法对弱间断和强间断的捕捉效果.两个激波管问题的计算域均取为[−0.5,0.5],初始条件分别为:

(1)SOD

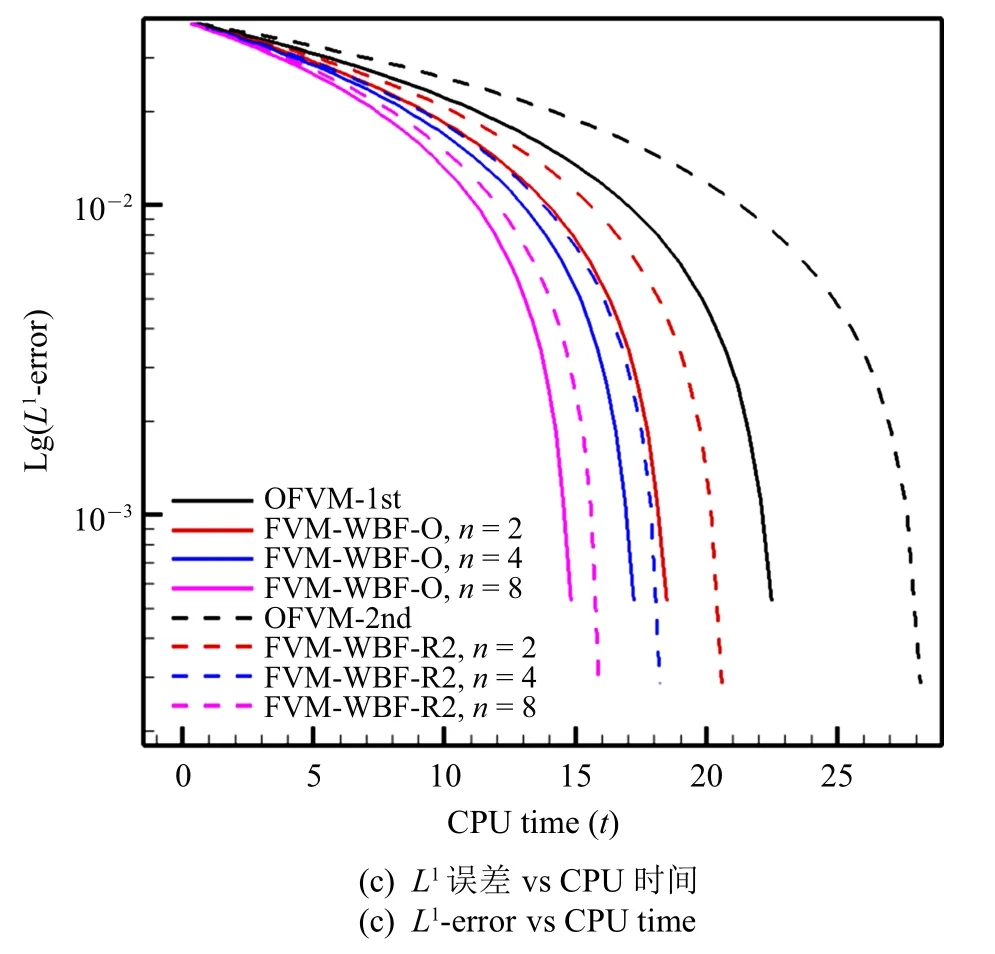
图3 一维Burgers 方程连续初值问题数值解Fig.3 Numerical results of continuous initial value problem of 1D Burgers equation

(2)LAX

均采用齐次Neumann 边界条件,网格量均为M=100.SOD 激波管问题计算到时间t=0.1,LAX 激波管问题计算到时间t=0.16.OFVM 方法与FVM-WBF方法对两个激波管问题的1 阶和2 阶计算所得数值密度的分布分别如图4 和图5 所示.通过对比激波、接触间断和稀疏波拐角等处的数值结果,可以发现,网格相同的情况下,FVM-WBF 方法对弱间断和强间断均有更好的捕捉效果,且对光滑解的模拟也有一定的改善.图4(c)和图5(c)给出的是两种方法的2 阶计算捕捉到的激波与网格尺度对比的放大图,其中灰色虚直线代表网格边界.可以看到一维FVM-WBF方法在n=4 和8 时均能达到小于网格尺度的激波捕捉效果.

3.3 二维无黏Burgers 方程间断初值问题

图4 一维Euler 方程SOD 激波管问题数值解Fig.4 Numerical results of SOD-shock tube problem of 1D Euler equations

图5 一维Euler 方程LAX 激波管问题数值解Fig.5 Numerical results of LAX-shock tube problem of 1D Euler equations

本算例求解了二维无黏Burgers 方程,比较了二维FVM-WBF 方法与OFVM 方法在相同网格上模模拟标量间断初值问题的效果.计算域为[−1,1]×[−1,1],初始条件为采用周期边界条件,计算到时间t=0.3,网格量为M=20×20.图6 展示的是两种方法2 阶精度的数值结果.其中,图6(a)和图6(b)是等值线图.在这两幅图中,同时给出了网格线以清楚地反映所得激波尺度与网格尺度的对比效果.图6(c)进一步给出了x=y截线上的数值解分布(图中灰色虚直线代表网格边界),可以发现FVM-WBF 方法中的n1和n2取2,4,8 时捕捉到的激波尺度都小于网格尺度,说明FVM-WBF方法在二维标量情况下能够达到网格内部捕捉间断的分辨率.

图6 二维Burgers 方程间断初值问题数值结果Fig.6 Numerical results of the discontinuously initial value problem of 2D Burgers equation

3.4 二维Euler 方程黎曼问题

二维Euler 方程的黎曼问题反映了多变气体的多尺度流场结构,一般由3 种常见的一维波(稀疏波,激波和接触间断波)相互作用形成.本算例在计算域[0,1]×[0,1]上考虑如下初始条件的黎曼问题[40]

采用齐次Neumann 边界条件,在相同的网格M=40 × 40 上比较了OFVM 方法与FVM-WBF 方法计算到t=0.3 时刻对激波的捕捉效果.图7(a)和图7(b)分别展示的是两种方法数值结果的密度等值线图.可以看到,相对于OFVM 方法,FVM-WBF 方法显著提高了激波间断的分辨率.取y=0.9 的截线,如图7(c)所示,可以发现FVM-WBF-R2 在n1,n2分别均取4 或8 时都能达到小于网格尺度的激波捕捉分辨率,而OFVM 方法捕捉的激波约为2 个网格尺度的宽度.该算例进一步说明FVM-WBF 方法在二维Euler 方程系统下也可以实现网格内部捕捉间断的效果.

图7 OFVM 和FVM-WBF 方法对二维Euler 方程黎曼问题的2 阶精度数值密度结果Fig.7 Numerical density obtained by 2nd-order OFVM and FVM-WBF method for Riemann problem of 2D Euler equations

3.5 Rayleigh-Tayler 不稳定性问题

Rayleigh-Tayler (R-T)不稳定性问题[41]描述的是,对于上下两层密度不同的流体,当密度大的流体受到重力影响流向密度小的流体时所产生的流动现象.经过一定时间的演化,轻流体的空泡和重流体的“尖顶”相互干扰,最终形成非常复杂的流场结构.

该算例的计算域为[0,0.25]×[0,1],初始条件为

另外,该算例还考察了两种方法计算相同时间步数时的计算效率.因为网格量相同时,FVM-WBF方法的自由度是OFVM 方法的n1·n2倍,所以理论上,计算相同的时间步数,FVM-WBF 方法消耗的CPU 时间应该是OFVM 方法的n1·n2倍,而自由度数目相同时,两者所耗费的时间应该相同,但测试结果显示并非如此.表5 给出了1000 个时间步时两种方法的CPU 时间对比.对于3 种基函数个数,OFVM 方法采用了与FVM-WBF 方法相同自由度数目的网格量.可以看到,自由度相同时,平均每个时间步FVMWBF 方法比OFVM 方法提高了约20%的计算效率,这可能是由于FVM-WBF 方法程序实现时数据结构存储方面带来的效益.未来可以从自适应算法的角度进一步提高FVM-WBF 方法的计算效率,相关的研究工作正在进行中.

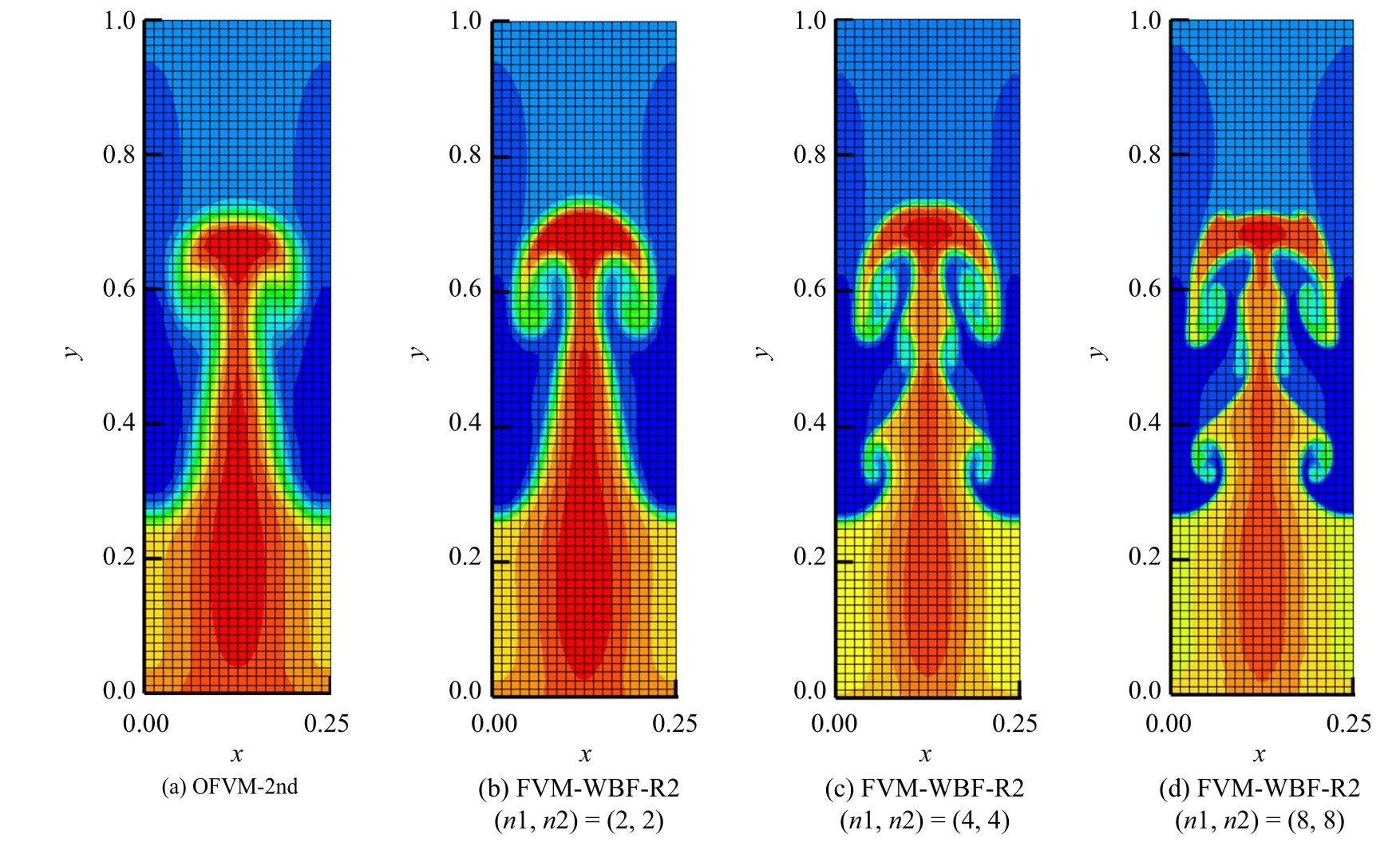
图8 OFVM 和FVM-WBF 方法对R-T 不稳定性问题的2 阶精度数值密度等值线图Fig.8 Density contours obtained by 2nd-order OFVM and FVM-WBF method for R-T problem

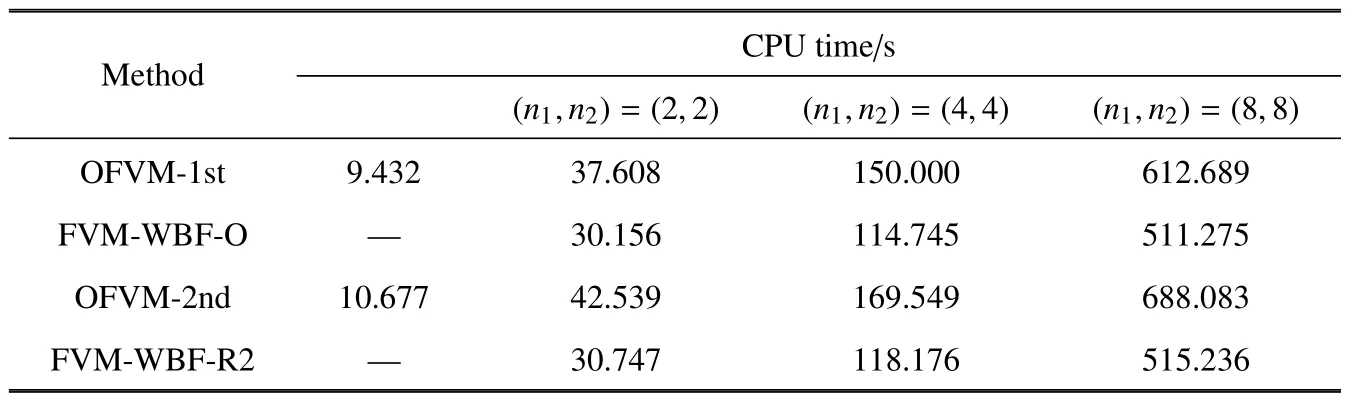
表5 FVM-WBF 方法与OFVM 方法计算效率比较Table 5 Comparison of computational costs between FVM-WBF and OFVM methods

4 结论

本文借助Walsh 基函数发展了一种可以在网格内部捕捉间断的新型有限体积方法,简称FVM-WBF方法.其基本原理是利用具有方波特性的Walsh 基函数在控制体内离散表示守恒变量,从而将间断配置在控制体内部.沿着间断位置将控制体划分为若干个连续的子单元,通过数值积分在子单元上对守恒型控制方程进行离散,求解以Walsh 基函数系数为解变量的离散控制方程,从而得到Walsh 基函数级数形式描述的数值解.文中理论推导和算例测试表明了FVM-WBF 方法具有高分辨率、高效率和良好的激波捕捉能力等优点,主要表现在:

(1)当FVM-WBF 方法与传统有限体积方法具有相同的收敛精度时,其误差缩减为传统有限体积方法的1/2p倍(p为所采用的Walsh 基函数级数截断对应的组数).因此,随着Walsh 基函数组数p的增大,FVM-WBF 方法的误差将以1/2 的p次方倍迅速下降,相应数值结果的分辨率也显著提高.

(2)当FVM-WBF 方法与传统有限体积方法具有相同的自由度时,收敛到相同的误差精度或计算相同的时间步数,FVM-WBF 方法都表现出更高的计算效率.

(3)FVM-WBF 方法在控制体内的子单元划分为有限体积高阶重构提供了新的可能的模板选择.本文采用子单元均值进行线性重构,得到了2 阶收敛精度的FVM-WBF 方法.与传统有限体积方法的2 阶计算结果相比,FVM-WBF 方法的2 阶计算依然表现出更高的激波捕捉能力,采用较少的Walsh 基函数(如2个或4 个)就能达到小于网格尺度的激波分辨率.

(4)FVM-WBF 方法在子单元上的积分离散与传统有限体积方法相同,所以传统有限体积方法中发展的各种成熟算法都可应用于FVM-WBF 方法.

另一方面,从文中的推导可以看到,将Walsh 基函数系数的守恒型控制方程在子单元上积分离散后,会得到关于Walsh 基函数系数的紧致型矩阵方程系统.因此,与通过扩展模板进行高阶重构实现高分辨的传统有限体积方法相比,FVM-WBF 方法更适用于并行方法的计算.而且随着基函数组数的增大,控制体内划分的子单元数目相应地按倍数增多,这也使得FVM-WBF 方法天然具有网格自适应和多重网格的潜力.这些特点应得到更为深入的研究,以期为CFD算法的探索和应用提供新的思路.