抽油泵固定凡尔球运动规律的数值模拟
2021-04-22王小兵吕雷纲龚浩宇王多琦
王小兵,吕雷纲,李 森,边 斌,刘 阳,龚浩宇,王多琦
(1.常州大学 石油工程学院,江苏常州 213164;2.Biological and Environmental Sciences and Engineering(BESE)Division,Water Desalination and Reuse Center(WDRC),King Abdullah University of Science and Technology,Thuwal 23955-6900,Kingdom of Saudi Arabia)
关键字:有杆抽油泵;固定凡尔球运动规律;多物理耦合;动网格;接触压力方法
0 引言
国内各油田大约80%的生产井使用有杆抽油技术,全国各大油田60%的产液量、75%的产油量是靠有杆抽油设备采出的[1]。抽油泵作为有杆抽油系统中核心的流体机械,工作原理是其固定凡尔球与游动凡尔球的周期性启闭控制泵内流体的吸入与排出。
通过试验对抽油泵固定凡尔球井下运动规律的测定有很大的困难,因此需要借助于数值模拟等方法。试验研究[2]表明了固定凡尔球的实际运动状态,但未能得出太多具有参考价值的结论;自1967年,ADOLPH[3]考虑固定凡尔球的受力以及运动特性,利用差分法构建了固定凡尔球运动规律的微分方程后,孟英峰等[4-8]从数学模型方面解决微分方程中的奇点问题、魏氏效应等。余海洋等[9]基于MATLAB,针对有杆抽油泵的上冲程阶段进行模拟研究,并探讨了流体的动力特性等因素对吸入特性的影响;吴建军等[10]借鉴前者的理论成果,通过Simulink对抽油泵固定凡尔进行仿真;李凌川等[11]基于FLUENT软件,结合动网格技术和UDF编程,对流体进泵的过程进行数值模拟得到了固定凡尔球的运动规律,在解决固定凡尔球与球罩的碰撞问题时采用了弹性恢复系数来描述固定凡尔球碰撞后的运动规律。以上文献存在一些未能解决的问题:建立的数值模拟对柱塞位移引起泵内体积增大的控制是依靠设置固定凡尔排出口为动边界,这对网格的影响极大,降低了计算的精度;对固定凡尔球与泵内壁面接触影响网格质量的解决方法并未具体说明,且研究中运用弹性回复系数描述凡尔球运动的方法忽略了流体阻力的影响。参考数值模拟在相关领域的研究[12-18],为现有的问题提供解决方案。针对以上问题,应用COMSOL Multiphysics 仿真软件,对黏性流体中抽油泵固定凡尔球的运动规律进行数值模拟;将CFD方法与固体力学耦合,并结合动网格技术以及接触压力方法,建立固定凡尔球的流固耦合模型。解决了上冲程阶段柱塞、固定凡尔球运动以及与其他固体壁面接触引起的网格变形和奇点问题,进而建立更加合理的固定凡尔球运动模型。研究结果得到了泵内流场分布以及固定凡尔球的运动规律曲线。所得结果为实际生产中抽油泵工作制度优化等提供了理论依据。
1 基本理论分析
1.1 假设条件
固定凡尔球做竖直向上的直线运动,而且伴随两种旋转运动,若柱塞运动速度较小时,固定凡尔球绕水平轴自上而下转动[2,19];当柱塞的运动速度较大时,固定凡尔球绕垂向轴水平方向自转,同时,沿阀座内孔边角绕球座孔轴线公转;因为泵筒体积狭小,横向的漂移很小。为简化计算,提出以下几点假设:(1)油井为直井,泵筒无倾斜;(2)阀球沿阀座中轴线运动,不考虑自转及公转;(3)柱塞与泵筒间不存在漏失;(4)泵内流体为油水混合物,且不含溶解气。
1.2 固定凡尔球的受力分析
在假设凡尔球不存在自转和公转的前提下,凡尔球的受力情况如图1所示。凡尔球在垂向上受到自身产生的重力G、浮力FB以及流体对凡尔球的绕球作用力FD三者的共同作用。此外,凡尔球与壁面碰撞时还应考虑接触压力。
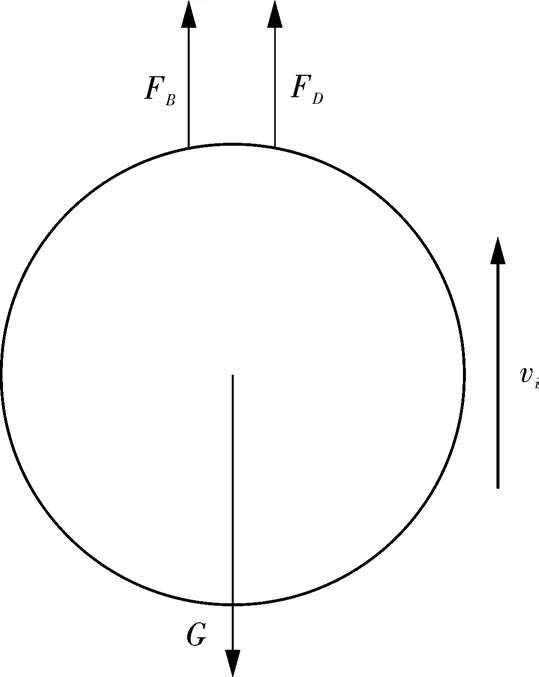
图1 凡尔球受力示意Fig.1 Schematic stress diagram of valve ball
2 基于COMSOL Multiphysics的多物理场耦合模型
单纯的CFD方法不能解决流体域与固体之间的接触压力问题,还需要考虑固体力学解决流体域中两固体的弹性碰撞问题。因此使用COMSOL Multiphysics建立流固耦合模型进行瞬态研究,耦合类型选择全耦合。完成模型选择之后,在模型开发器界面中主要包含组件和研究两个部分。组件中完成几何模型、边界条件及网格的设置,研究中选择求解器和时间步长。
2.1 几何模型
抽油泵固定凡尔是轴对称结构,所以选择二维轴对称的空间结构进行抽油泵固定凡尔几何模型的建立能节约计算内存且节省计算时间。研究外径70 mm的固定凡尔,几何模型如图2所示。
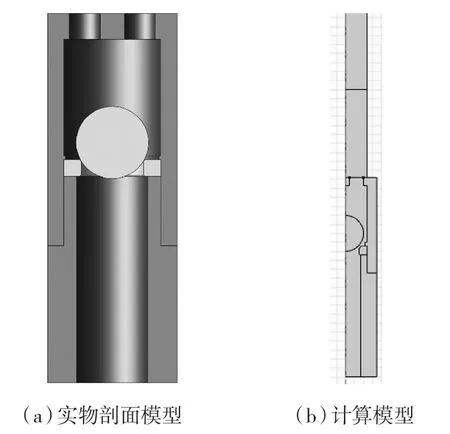
图2 抽油泵固定凡尔的几何模型Fig.2 The geometric model of the standing valve of the oil well pump
2.2 抽油泵固定凡尔的物理模型
抽油泵固定凡尔的物理模型包括流体流动模型和固体力学模型,流体流动模型通过对雷诺数的计算选择层流或是湍流;固体力学模型通过材料属性选择研究对象为线弹性材料、非线弹性材料或其他。抽油泵固定凡尔球的打开或关闭都会使泵内形成狭窄流道,则流动形态为湍流,湍流模型中的k-ε模型对于复杂几何周围外部流动问题的求解效果良好,因此流体流动模型选择k-ε模型,考虑流体可压缩性且包含重力。抽油泵及其配件的材料为钢质,则固体力学模型的研究对象确定为线弹性材料,对凡尔球设置重力,指定柱塞位移,其他部件设置为固定。
2.3 接触压力方法
柱塞未开始运动时,固定凡尔球由于重力原因落在球座上从而关闭吸入口,速度为零,此时固定凡尔球上下两部分的流体不连通、流体连续性被破环,从而出现了奇点问题。根据机械密封理论[20],固定凡尔球与球座的接触面有一层液体薄膜,说明保证流体连续性即通过数学方法给固定凡尔球与泵内会产生接触的壁面设置偏移距离实现对奇点问题的解决。
首先,在模型开发器界面中组件的定义节点中添加接触对,选择凡尔球的壁面为源边界、选择球座及球罩的接触壁面为目标边界如图3所示。
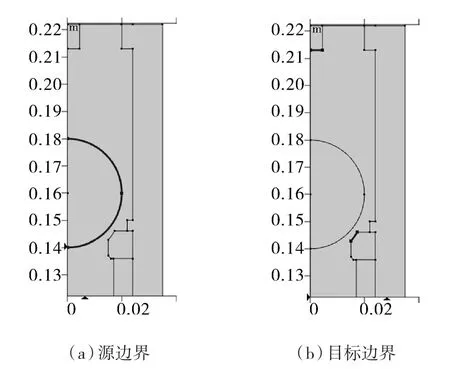
图3 定义壁面的接触对Fig.3 Definition of the contact pair of the wall
其次,在组件中的固体力学模块中添加接触节点,选用定义的接触对;接触压力方法选择罚函数;偏移距离的设置需要重复测试,最后优化为5 μm。该方法在不影响壁面接触压力的同时实现了流体的连续性,从而解决了凡尔球与泵内壁面的接触引起的网格问题。
2.4 动网格及网格划分
固定凡尔球运动时必须使用动网格技术适应边界的运动或变形。在动网格节点中,添加变形域节点并选择所有流体域,网格平滑类型选择Yeoh(更易于收敛);添加固定边界节点并选择出入口边界以及固体壁面;添加指定网格位移节点并选择会发生移动的所有边界。
对柱塞段的网格划分采用映射网格,选择分布方法对各边界上的网格数量进行定量划分,从而解决了大变形以及网格大量的重复划分造成的内存不足问题。对固定凡尔的网格划分采用自由三角形网格,并添加边界层和角细化对边界进行处理,对流体域进行加密、固体域适当粗化,网格如图4所示。
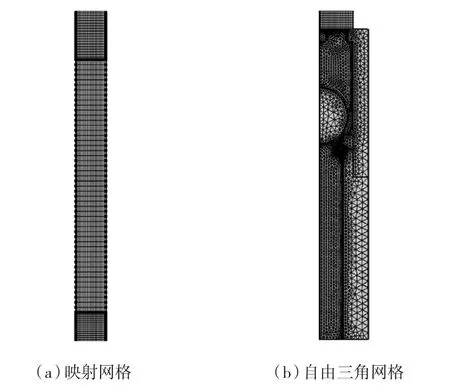
图4 网格划分Fig.4 Mesh division
2.5 自动重新划分网格
固体域位置的不断变化会导致网格质量变差,所以对大位移的模型要进行自动重新划分网格的设置。自动重新划分网格的操作步骤:在研究的步骤节点中,选用自动重新划分网格;然后获取求解器配置的初始值,在求解器配置节点中的瞬态求解器中设置自动重新划分网格的条件,选择条件类型为失真并设置超出失真范围时停止为1。
2.6 固定凡尔球的初始位置
当柱塞未开始工作时,固定凡尔球落于球座上并关闭吸入口。在几何模型的绘制时将固定凡尔球与球座进行配合,会破坏流体域连续性的网格拓扑结构,则凡尔球最初需要一段初始距离使固定凡尔球在重力作用下落在球座上,同时这一过程要对接触压力方法以及偏移进行调整优化。对柱塞位移施加时间条件,固定凡尔球因重力下落在球座上,时间控制函数为:(t[1/s]> 0),该函数表示与时间相关的变量从0 s开始施加,从而为模型计算提供了合理的初始值。
时间步设置为(-t0,Δt,t1),表示开始计算之前的t0时间段内固定凡尔球落于球座上,完成凡尔球初始位置的设定。在开始计算时,突然施加入口压力改变会导致计算错误,因此在入口压力边界写入阶跃函数,从而解决压力突变造成计算的不收敛。
3 结果分析
模型的计算参数为:固定凡尔外径70 mm、腔体内径48 mm,凡尔球直径40 mm,球座厚度10 mm、内径30 mm,吸入口直径34 mm;泵筒上端流域长5 m、内径48 mm;固定凡尔、凡尔球、球座的材料均为钢质,密度为7 850 kg/m3、杨氏模量为210 GPa、泊松比为 0.3;泵内流体黏度为 10 mPa·s、密度为900 kg/m3;上冲程阶段游动凡尔球关闭,以固体域近似为柱塞,长度为0.6 m。入口压力为3 MPa,出口压力为10 MPa,柱塞冲程为3 m、冲次为6 r/min,下泵深度为1 000 m。研究该工况下固定凡尔球的运动规律,分析柱塞冲次和泵内流体粘度对固定凡尔球运动的影响。
3.1 固定凡尔运动规律分析
抽油泵固定凡尔球的位移曲线和打开程度反映了凡尔球打开的响应速度,所得结果如图5所示。

图5 固定凡尔球运动规律曲线Fig.5 Motion curve of the standing valve ball
由图5可知:泵内流体为油水混合物且不含气体时,泵内较小的空间内液体体积膨胀很微弱,凡尔球的打开过程几乎不存在滞后现象,在柱塞上行的同时固定凡尔球打开;随着柱塞的不断上行,凡尔球上升高度越来越高,且运动过程中有一定的波动并且在两个时间点存在明显的小幅度回落,最大升程为3.88 mm,所需开启时间为2.43 s;在整个上冲程阶段,固定凡尔球并未到达球罩所在高度而是在一定高度处悬浮,且柱塞上行的后半段(柱塞的减速上升阶段),固定凡尔球逐渐回落且最终几乎关闭吸入口,滞后关闭时间较短。
3.2 冲次对固定凡尔球位移的影响
研究的冲次范围为 2,4,6,8,10 r/min,得到固定凡尔球的运动规律曲线如图6所示。
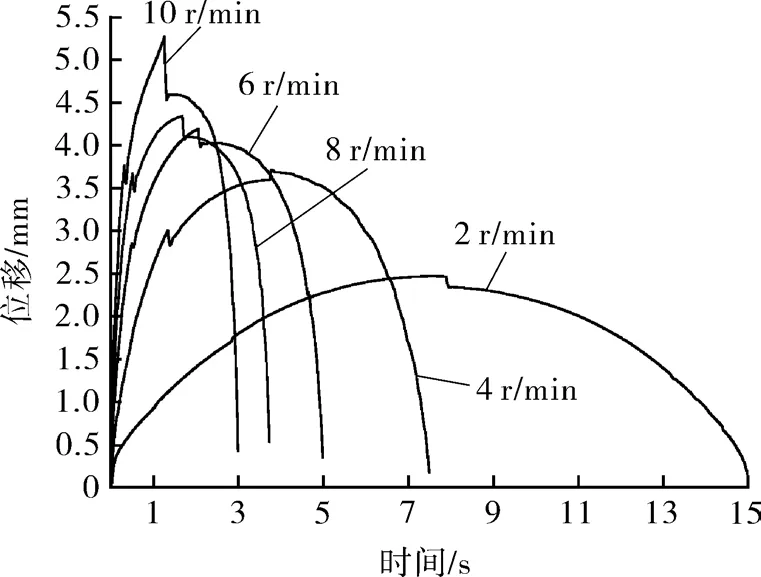
图6 冲次对固定凡尔球升程的影响曲线Fig.6 The influence curve of times of stroke on the motion law of standing valve ball
由图6可知,冲次越高固定凡尔球运动过程中的波动性越强且运动过程中出现的瞬间回落或者上升的幅度越大;在研究的冲次范围内,固定凡尔球都未到达球罩所在高度而是在一定高度处悬浮,冲次越高升程越高;在柱塞上行的后半段(柱塞的减速上升阶段),固定凡尔球逐渐回落且最终几乎关闭吸入口,冲次越高关闭程度越小。冲次越高升程越大,所需的开启时间越短;当冲次为2 r/min,最大升程为2.46 mm,所需开启时间为7.38 s;当冲次为4 r/min,最大升程为3.71 mm,所需开启时间为3.8 s;冲次为6 r/min,最大升程为3.88 mm,所需开启时间为2.43 s;当冲次为8 r/min,最大升程为4.33 mm,所需开启时间为1.7 s;当冲次为10 r/min,最大升程为5.26 mm,所需开启时间为1.27 s。
3.3 泵内流体黏度对固定凡尔球位移的影响
研究的泵内流体黏度为 10,30,50,70,90,110 mPa·s,并确定出凡尔球完全打开时的临界黏度,得到固定凡尔球的运动规律曲线如图7所示。
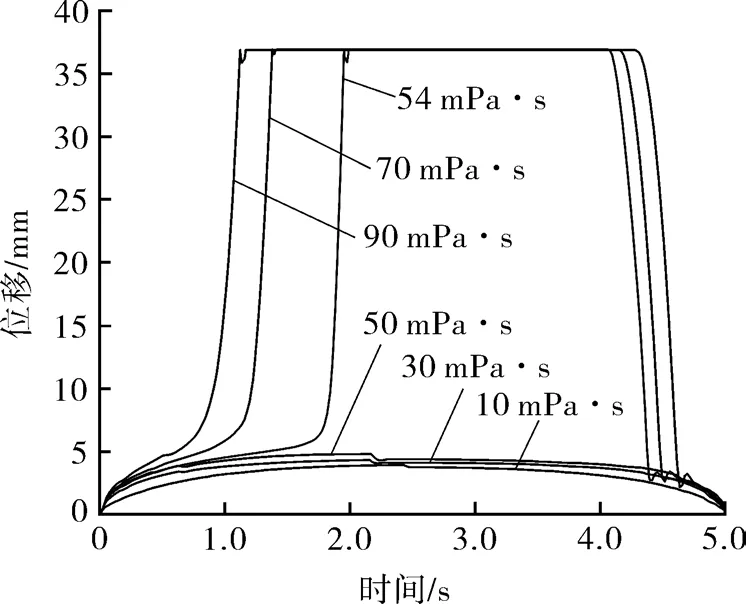
图7 泵内流体黏度对固定凡尔球位移的影响曲线Fig.7 The influence curve of viscosity of fluid in pump on the motion law of standing valve ball
如图7所示,在研究的泵内流体黏度范围内,黏度小于54 mPa·s(临界黏度)时,凡尔球的打开程度随泵内流体黏度的增大而增加,但未完全打开;黏度大于54 mPa·s时,固定凡尔球完全打开,且黏度越大打开时间越短;当凡尔球由于球罩限制,与其发生碰撞时,凡尔球经过反弹后在流体作用力下悬浮在球罩处;在柱塞上行的后半段(柱塞的减速上升阶段),固定凡尔球逐渐回落且最终几乎关闭吸入口,黏度越高滞后关闭时间越长,且黏度大于54 mPa·s时,固定凡尔球在接近球座时波动性更强。流体黏度越高固定凡尔球的升程越大,固定凡尔球达到最大打开程度所需开启时间越短,黏度为10 mPa·s,最大升程为3.88 mm,所需开启时间为2.43 s;当黏度为30 mPa·s,最大升程为4.29 mm,所需开启时间为2.16 s;黏度为50 mPa·s,最大升程为4.77 mm,所需开启时间为2.17 s;黏度为54 mPa·s时,固定凡尔球完全打开,所需开启时间为1.42s;流体黏度为70 mPa·s,固定凡尔球完全打开,所需开启时间为1.28 s;流体黏度为90 mPa·s,固定凡尔球完全打开,所需开启时间为1.17 s。
4 结论
(1)构建抽油泵固定凡尔球的流固耦合模型运用了动网格技术及接触压力方法,对入口压力边界结合阶跃函数解决了奇点问题和固定凡尔球与泵腔内壁面的接触问题,从而为柱塞泵球形凡尔的流体机械设计、优化提供了数值模拟方法。
(2)冲次增加固定凡尔球的升程增加,但在研究范围内固定凡尔球完全打开;冲次增加对固定凡尔球上升过程的稳定性有不利影响,冲次越高越易引起固定凡尔球在实际工作中与其他壁面碰撞的机会,造成球体损坏引起的流体漏失,降低泵效。
(3)泵内流体黏度越高固定凡尔球的升程越高所需开启时间越短;黏度54 mPs·s时为临界黏度,小于54 mPa·s时固定凡尔球不能完全打开,大于54 mPa·s时固定凡尔球完全打开,与球罩产生碰撞并有较小幅度的反弹,最终稳定在球罩出,泵内流体黏度对固定凡尔球的开启程度影响显著。
(4)对冲次和泵内流体黏度的分析为有杆抽油泵的工作制度优化提供了理论参考。
