高镁贫镍红土矿碳还原动力学

彭 博 王宇鲲 魏永刚

(1.昆明理工大学 省部共建复杂有色金属资源清洁利用国家重点实验室，昆明 650093；2.昆明理工大学 冶金与能源工程学院，昆明 650093)

镍是一种重要的金属，具有抗氧化、耐腐蚀、耐高温、延展性好、强度高等优点，被广泛用于生产不锈钢、金属电镀、燃料电池等[1]。世界范围内可开采的镍资源大约有70%是红土镍矿[2]。目前，镍的冶炼近70%来源于硫化镍矿，但是随着镍需求的增加以及硫化镍矿的日渐枯竭，研究焦点正逐渐向红土镍矿转移。红土镍矿是由含镍的橄榄石岩在潮湿气候下通过化学风化沉积形成的[3]。在风化过程中，镍逐渐向不同的次生矿物中聚集。红土镍矿矿床通常可分为褐铁矿层、过渡层和腐殖土层三个部分[4]。褐铁矿层靠近地表，含大量针铁矿[5]，矿床铁含量较高，镁含量较低。腐殖土层主要为硅镁型红土镍矿，含有利蛇纹石、石英和磁赤铁矿，具有低铁高镁的特点。

国内外学者对红土镍矿动力学进行了大量的研究，如PICKLES[1]对褐铁型红土镍矿的干燥动力学进行了研究，确定了红土镍矿脱水过程的控制步骤。JANKOVI等[6]报道了氢气还原氧化镍的动力学研究，得到了氧化镍和氢气反应过程的相关动力学参数，以及反应符合的动力学模型。李博等[7]对红土镍矿固相动力学进行了研究，给出了红土镍矿一定温度范围内的分解机理以及动力学参数，并借此分析了红土镍矿还原机理。LI等[8]还研究了以一氧化碳为还原剂的不同氧化铁-氧化镍复合物的非等温还原动力学和机理。目前对红土镍矿的动力学分析大多是红土镍矿脱水、分解以及纯物质Fe2O3、NiO还原等方面的研究，但对红土镍矿碳还原动力学的研究却鲜有报道。基于此，本文主要研究还原过程高镁贫镍红土矿碳还原动力学特征，采用非等温动力学研究方法，在多重升温速率条件下对样品进行热重实验，获得样品质量随温度升高的变化曲线，并利用热分析动力学的微分法(Kissinger)与积分法(Flynn-Wall-Ozawa，FWO)对碳热还原反应过程进行动力学分析。两个计算方法可避免因反应机理函数的选择可能带来的误差。首先根据热重曲线变化规律分阶段研究了反应过程最大反应速率与温度的对应关系，采用Kissinger微分法计算反应活化能，随后由FWO积分法计算整个碳热还原反应过程表观活化能，以此验证高镁贫镍红土矿碳热还原的多步反应特点，获得的研究结果为进一步揭示还原焙烧过程红土镍矿碳还原机理以及红土镍矿的火法处理提供理论借鉴。

1 实验

1.1 原料

实验用试样为云南某地区红土镍矿，其主要化学组成见表1，XRD分析结果如图1所示。可知，矿中Ni含量低，MgO含量高，属于高镁贫镍红土矿。可见该红土镍矿的主要物相为利蛇纹石、石英及磁赤铁矿。将实验所用红土镍矿在650 ℃下预焙烧脱除自由水，且物相发生由利蛇纹石相转为橄榄石相的相变，预焙烧后的红土镍矿XRD图谱见图1。实验用还原剂碳为分析纯试剂。

图1 红土镍矿和预焙烧红土镍矿的XRD图谱Fig.1 XRD patterns of laterite ore and preroasting laterite ore

表1 红土镍矿化学成分

1.2 实验方法

称取5 g预焙烧矿，添加6%的分析纯碳，并充分混匀。用电子天平称300 mg样品放入坩埚中，再将坩埚置于热重仪器称量托盘上，向热重仪器内部通入一定流速的氮气以排出空气，并在仪器匀速升温至1 300 ℃的过程中持续通入30 mL/min的氮气，实验结束后冷却至室温将样品取出。所有热重实验均使用HTG-1型热重设备在氮气气氛(30 mL/min)下进行。采用三个线性升温速率(5、10、20 K/min)的数据对粉末状样品进行动力学研究。

1.3 动力学方法

气-固反应的动力学分析数据可以在不同的条件下得到，这里分析的数据是在非等温条件下获得的，随着时间的推移温度呈线性上升(β=dT/dt，β是升温速率，T是温度，t是时间)。在这样的条件下，反应速率可以用一般式表示：

dα/dt=Af(α)exp(-Ea/RT)

(1)

式中，α—转化率，%；A—指前因子；Ea—活化能，J；f(α)—转化率和反应过程的关系；R—摩尔气体常数。式1用Ea、A、f(α)来表示反应过程中的物理或化学变化。

1.3.1 Kissinger法

Kissinger法通过线性升温实验中反应速率极大值点的升温速率对数和温度的倒数作图来确定固态反应的表观活化能[9]，见式2。

(2)

式中，β—升温速率，K/min；Tmax—质量损失率极大值点处的温度，K；αmax—质量损失率极大值点处的转化率，%；n—反应级数。n为1时，n(1-αmax)n-1≈1，由Kissinger得出式 3。

(3)

1.3.2 Flynn-Wall-Ozawa法

Flynn-Wall-Ozawa(FWO)法通过线性升温实验中等转化率点的升温速率对数和温度的倒数建立方程[10]，基本形式见式 4。

lnβ=ln(AEa)/(Rg(α))-5.331-1.052Ea/RT

(4)

式中，g(α)—反应模型积分形式的代数表达式，当α相同时，可将lnβ与1/T进行线性拟合，并通过斜率得到表观活化能。

2 结果与讨论

2.1 热力学分析

硅镁型红土镍矿中金属氧化物的还原主要分为以下两步：固定炭直接与矿石中的金属矿物发生固-固直接还原反应；炭直接还原金属氧化物产生的CO以及布多尔反应产生的CO与矿石中的金属矿物发生气-固还原反应[7]。炭直接还原金属氧化物的主要反应为式5、6，对应的标准吉布斯自由能与温度的关系如图2所示。可以看出Fe2O3在270 ℃开始就可以被还原成Fe3O4。NiO的直接还原也很容易发生，在430 ℃就可以开始反应。

3Fe2O3+C=2Fe3O4+CO

ΔGθ=120.00-0.22T(kJ/mol)

(5)

NiO+C=Ni+CO

ΔGθ=126.60-0.18T(kJ/mol)

(6)

图2 反应(5)和(6)的标准吉布斯自由能Fig.2 Standard gibbs free energy of reactions 5 and 6

在上述固-固反应过程中，产生的CO可作为气体还原剂参与矿石中金属氧化物的还原，反应方程式如式7～9所示。还原产生的CO2可与C发生布多尔反应生成CO，反应方程式为式10。CO还原矿石中金属氧化物的标准吉布斯自由能如图3所示。由图3可知，在实验温度范围内，NiO与CO的反应吉布斯自由能小于零，表明NiO容易被CO还原。当温度在611 ℃以上时，Fe3O4能够被CO还原成FeO，FeO也较易被CO还原。

Fe3O4+CO=3FeO+CO2

ΔGθ=35.38-0.040T(kJ/mol)

(7)

FeO+CO=Fe+CO2

ΔGθ=-22.80+0.024T(kJ/mol)

(8)

NiO+CO=Ni+CO2

ΔGθ=-48.32+0.0019T(kJ/mol)

(9)

C+CO2=2CO

ΔGθ=170.70-0.17T(kJ/mol)

(10)

图3 反应7、8和9的标准吉布斯自由能Fig.3 Standard gibbs free energy of reactions 7，8 and 9

2.2 红土镍矿碳还原动力学

图4为样品在三种升温速率(5、10、20 K/min)条件下的质量损失率与温度关系曲线。显然三条曲线的质量损失率均随着温度的升高而增加，最终约为10.1%。并且升温速率对曲线也有一定影响，相同温度处的质量损失率随着升温速率的增加有降低的趋势，这一现象在600～1 000 ℃尤其明显。

图4 红土镍矿碳还原TG曲线(5、10和20 K/min，N2气氛)Fig.4 TG curves for carbon reduction of laterite(5，10 and 20 K/min，N2 atmosphere)

图5为样品转化速率—温度关系曲线。显然，在700 ℃左右时dα/dt出现第一次峰值，此后开始减小，并在1 000 ℃左右再次增加。结合图4分析，反应在1 200 ℃基本结束。综合所进行的热力学分析，可将样品反应过程分为两步，第1步主要在500～800 ℃，发生样品中金属氧化物与固相还原剂的反应，主要由Fe2O3与C反应生成Fe3O4固体和CO气体；第2步为800 ℃至升温结束，失重反应包括7～9，升温至800 ℃以后，布多尔反应产生的气体还原剂CO，样品中的金属氧化物发生气-固反应[11-12]。

图5 红土镍矿碳还原的反应速率曲线(5、10和20 K/min，N2气氛)Fig.5 Reaction rates curves for carbon reduction of laterite(5，10 and 20 K/min，N2 atmosphere)

由图5可得表2为升温速率对红土镍矿碳热还原特征温度的影响，不同升温速率下达到反应速率极大值时的特征温度Tp1和Tp2见表2。由表2可得，反应速率曲线随着升温速率的增加有向高温处偏移的现象，Tp2之间的差值比Tp1之间的差值更大。

表2 升温速率对红土镍矿碳热还原特征温度的影响

由式3可知，通过多个线性升温速率实验可得到求解反应活化能的线性方程，且对反应模型没有限制。图6为基于Kissinger方法得到的线性拟合直线，由斜率和截距可求得Ea与A。计算得到第一步骤活化能为260.4 kJ/mol，lnA=29.91/min。第二步骤活化能为191.2 kJ/mol，指前因子lnA=17.8 1/min。第2步骤主要是气-固反应，由于气体扩散较快，与金属氧化物接触面积较大，反应较容易进行，因此第2步的活化能比第1步的低。

图6 不同升温速率的T与关系Fig.6 Different rates of heating versus T

图7显示了样品的转化率—温度关系曲线。反应第1步的最大速率出现在750 ℃左右，对应的转化率α约为0.5，第2步的最大速率出现在1 100 ℃左右，对应的转化率α约为0.8。可根据Flynn-Wall-Ozawa(FWO)法求得转化率α=0.2～0.9的活化能值。

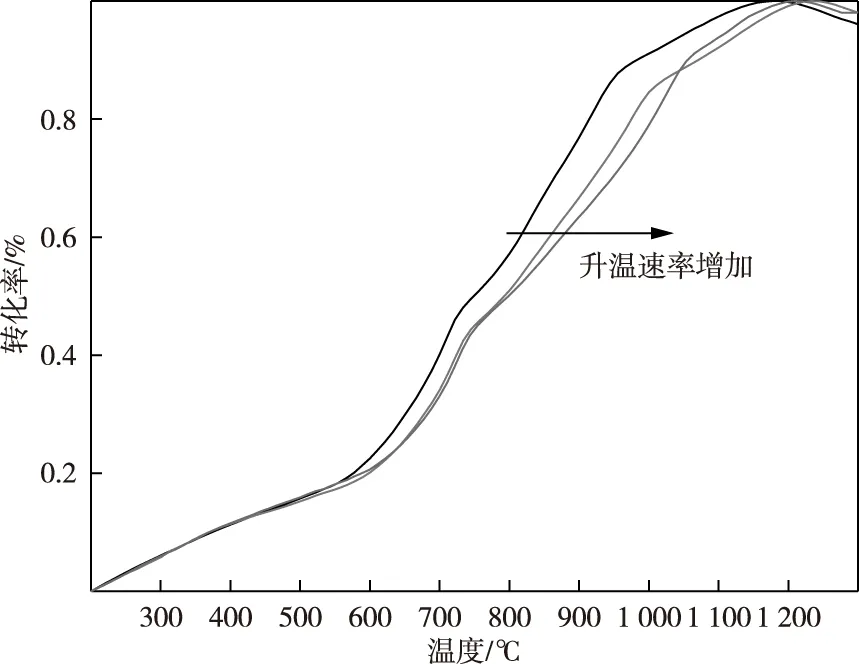
图7 红土镍矿碳还原转化率α随温度的变化(5、10、20 K/min，N2气氛)Fig.7 The conversion rate α of carbon reduction of laterite was changed with temperature(5，10 and 20 K/min，N2 atmosphere)

将三个升温速率下相同转化率α时的温度T与β根据式4进行线性拟合，将α在0.2～0.9内每隔0.1取一点进行线性拟合见图8，可得到拟合度较好的8条直线。

图8 lnβ与1/T的关系图Fig.8 The relationship of ln β and 1/T

表3为根据图8和式4计算的Ea值和相关系数R，由R值可知拟合程度较高，能够求出较为可靠的Ea值，反应第2步的Ea值比第1步的更小。

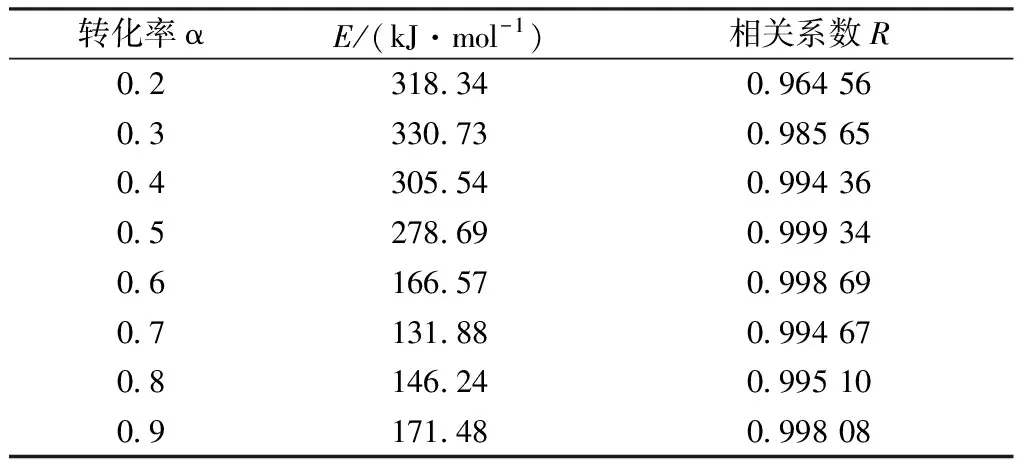
表3 FWO法计算得到的活化能

图9为表3所得Ea值与α的折线图。由图9可知，活化能在转化率α为0.2～0.4时较高，结合热力学分析，此时对应的反应为固-固反应，α从0.5增加到0.6的过程中，活化能突然降低，原因在此温度下发生布多尔反应，反应由固-固反应转变为气-固反应。由于金属氧化物较易被CO还原，因此活化能较低。α>0.6后活化能基本趋于稳定，再次证明红土镍矿碳还原过程可分为两个步骤。第一步是碳和金属氧化物固-固直接还原，第二步是CO与金属氧化物气-固还原。

图9 基于FWO方法的转化率与反应活化能关系Fig.9 The conversion rate and reaction activation energy relationship based on FWO method

3 结论

1)不同升温速率下的质量损失率均随着温度的升高而增加，而转化速率曲线呈现出两个峰值且在700 ℃有最大值。升温速率对红土镍矿碳还原也有一定影响，相同温度处的质量损失率随着升温速率的增加有降低的趋势，这种趋势在600～1 000 ℃内尤其明显。可以将反应分为500～800 ℃和800～1 300 ℃两个步骤。

2)使用Kissinger法计算得到两个步骤的反应活化能分别为260.4 kJ/mol和191.2 kJ/mol，指前因子分别为lnA1=29.9 min-1和lnA2=17.8 min-1。FWO法计算得到的Ea值随着α值的变化较大，表明还原过程由多个反应组成。

3)高镁贫镍红土矿碳还原过程的第1步主要是金属氧化物与固相还原剂的反应，生成磁性铁、镍和CO；第2步主要是CO与磁性铁反应生成FeO，FeO、NiO与CO反应生成镍铁合金，以及CO2和C的布多尔反应生成CO。