祁连山南麓区域的大气负荷动力学效应研究
2021-04-22安旭伟杨国林孙学先
安旭伟,杨国林,孙学先,刘 涛,张 波
祁连山南麓区域的大气负荷动力学效应研究
安旭伟1,2,杨国林1,孙学先3,刘 涛1,张 波1,2
(1. 兰州交通大学 测绘与地理信息学院,兰州 730070;2. 地理国情监测技术应用国家地方联合工程研究中心,兰州 730070;3. 甘肃省地理国情监测工程实验室,兰州 730070)
地壳形变的大气负荷效应在沿海区域已得到了广泛研究和应用,但是在内陆地区,动力学效应研究甚少。基于地面气象观测数据和全球气压模型数据,给出了一种适合于内陆地区的大气负荷动力学效应的计算方法。以中国祁连山南麓地区为例,研究了地壳形变和地面重力变化。研究结果表明:对于祁连山南麓地区,大气负荷对测站位移径向分量的影响约为8.4 mm,而水平位移不足1.0 mm;对测站重力的影响约为6.4×10-8m/s2。大气负荷的动力学效应具有明显的周期性和季节性,这种变化规律与周边地区表现出较高的一致性。
球谐分析;移去恢复;负荷格林函数;大气导纳
0 引言
受各种地球动力学因素的影响,地球重力场和地面站点位置会随时间发生变化。其中大气负荷潮指的是,大气在日月引潮力和太阳热辐射的共同作用下,表现出的大气压周期性变化[1],在高精度的大地测量计算过程中,大气负荷改正是不能被忽略的[2-4]。文献[5]提出了大气负荷效应的负荷格林函数积分法与球谐函数法;文献[2]基于朗曼(Longman)地球负荷理论,提出了静态格林函数法;文献[4]对中国6个全球定位系统(global positioning system, GPS)基准站的大气负荷效应进行了研究,指出测站径向位移的大气负荷效应可达2~3 cm;文献[6-8]利用球谐函数方法,给出了地表流体质量负荷变化的动力学效应公式;文献[9]利用全球大气压实测数据,计算了大气负荷对地面重力变化的影响;文献[10]结合地表水、大气及海平面变化资料,提出了负荷形变场精化模型的已知负荷移去恢复法,建立了地面稳定性变化定量辨识准则。目前,将文献[10]理论应用于高原地区的研究成果相对较少,因此,有必要将这种方法落实到具体的某一个高原地区,定量分析大气负荷对内陆地表的影响。
本文在全球大气数据的基础上,结合祁连山南麓区域内气象站的实测气压数据,计算了大气负荷对区域内地壳形变以及地面重力变化的影响,目的是分析具体影响量级,从而获得大气负荷效应的变化规律以及影响量。
1 负荷形变理论与移去恢复法
1.1 负荷形变理论
大气负荷引起的地壳形变与重力变化都可以用相应的等效水高变化来表示[11],即
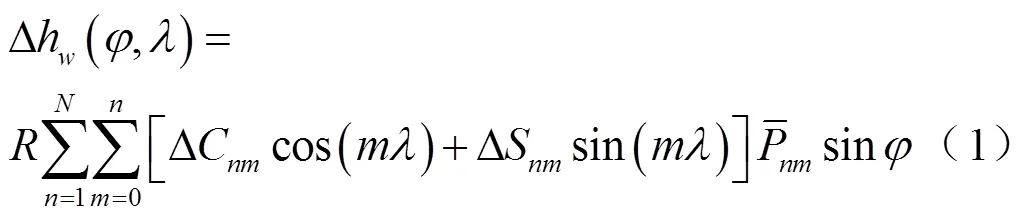



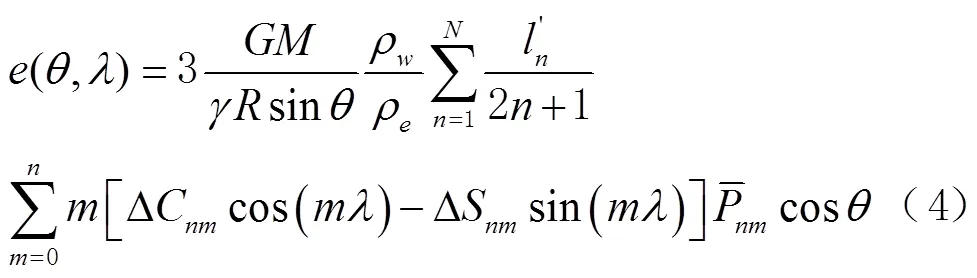
1.2 移去恢复法
移去恢复法主要流程见图1。
2 研究区域和数据
2.1 研究区域
本文研究区域为(93.5°E~99.0°E,34.5°N~38.0°N),如图2所示。

图2 研究区域及气象站点示意
2.2 数据来源
本文研究的全球大气数据源自欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)[13],该类数据的特点是覆盖范围广、要素种类多、分辨率较高、记录数据时次多等。使用的区域大气压数据来自于寒旱区科学数据中心的中国大气同化驱动数据集(The China Meteorological Assimilation Driving Datasets for the SWAT Model, CMADS)[14],使用的是日均值气压数据,精度为0.1 hPa。数据处理过程中,需要将空间分辨率改变为0.05°×0.05°,并使用派森(Python)程序将其转换为月值数据。
3 地壳形变和重力变化计算分析
3.1 大气负荷对地壳形变的影响
为了方便计算,本文使用的全球气压等效水高基准是2011年10—12月,共3个月的月均值,所有的变化都是基于这一基准而言,计算了2012年1月—2017年12月,共6年的大气负荷对地壳形变的影响。
本文选取2015年3月、6月、9月与12月大气负荷对地壳形变场影响的空间分布进行分析,其中水平形变包括北方向以及东方向两个部分,先分别计算,然后再进行矢量合并,最后得到水平形变量的大小(矢量模的大小)。根据计算大气负荷对祁连山南麓区域内地壳形变的影响,其变化规律具有明显的年周期性。区域影响变迁图如图3、图4所示。
由图3,图4可知,大气负荷对地壳垂直形变影响的最大变化量出现在德令哈周边区域,大约为7.5 mm,这与该地区当年气压变化量较大相符。而对水平形变的影响量较小,即使格尔木附近出现了最大水平形,但其变化变量也不足1.0 mm。就周期变化规律而言,大气负荷对地壳形变影响在春夏季呈增大趋势,在6月份左右达到最大,在秋冬季呈减小趋势,在12月份左右降至最小。由于地表环境的复杂性,可能导致2012年、2013年、2015年的垂直形变最小值出现时间提前到10月份。就6年地壳形变的总体规律而言,与该区域夏季气温高、昼夜温差较大,所引起的地表特征变化活跃相符合。

图3 2015年大气负荷对地壳垂直形变的影响
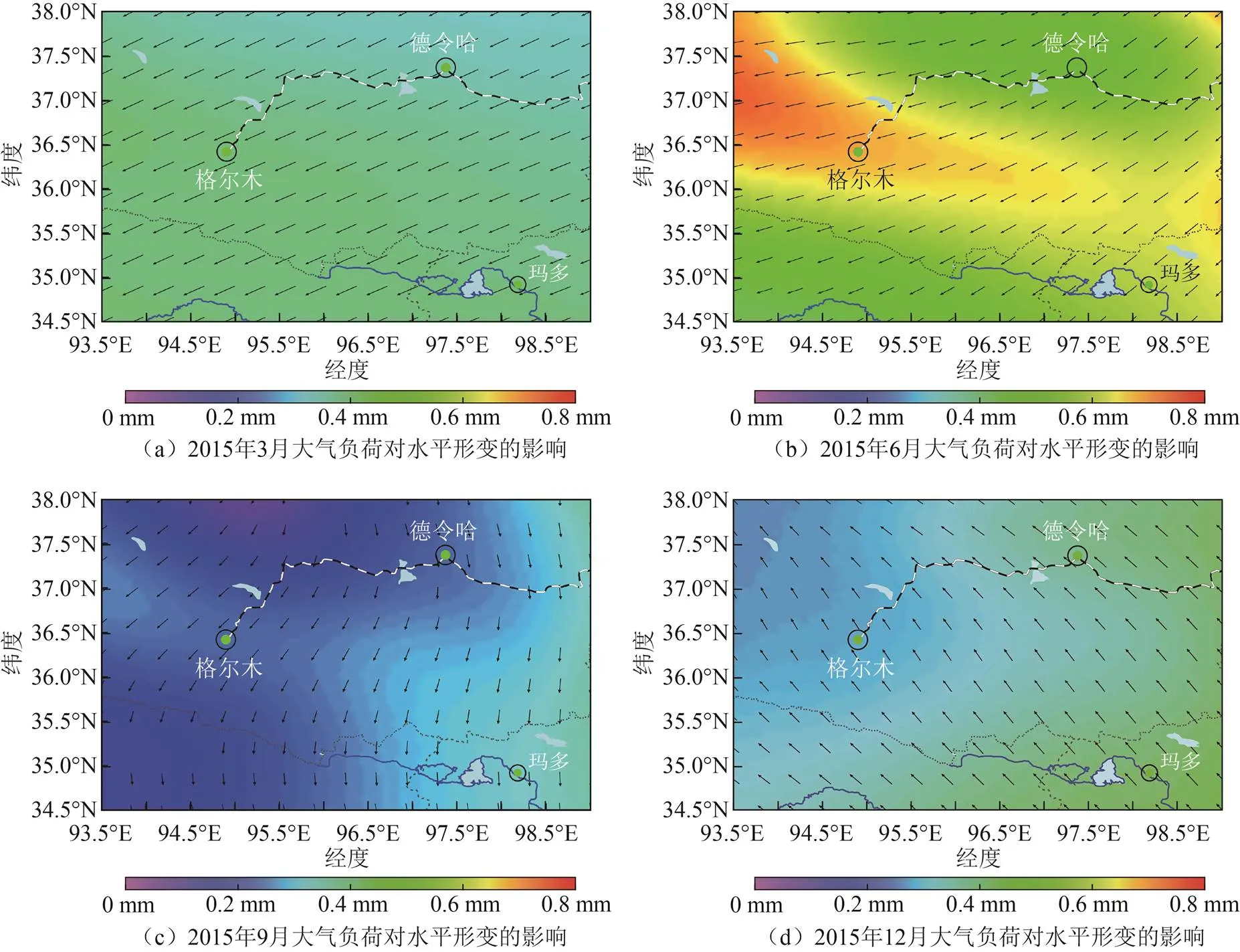
图4 2015年大气负荷对地壳水平形变的影响
3.2 大气负荷对地面重力的影响
大气负荷对地面重力变化总影响还包含直接影响,可以由大气导纳的方式求得[15],然后将两种影响结果相加即得重力变化的总影响,本文选取了2015年3月、6月、9月与12月大气负荷对地面重力影响的空间分布进行分析,如图5所示。
由图5可知,大气负荷对祁连山南麓区域的地面重力呈现周期性规律,春夏季主要表现为增大趋势,在6月份左右达到最大值5.4×10-8m·s-2,较为显著的空间分布出现在德令哈地区。秋冬季主要体现为减小趋势。就整个研究区域祁连山南麓而言,年变化幅度可达6.4×10-8m·s-2。就6年地面重力变化总体来看,每年最大值出现的情况比较规律,一般在6月份左右;相比之下,最小值会提前到9月份、10月份出现,这可能与该地区复杂的地表环境有关。
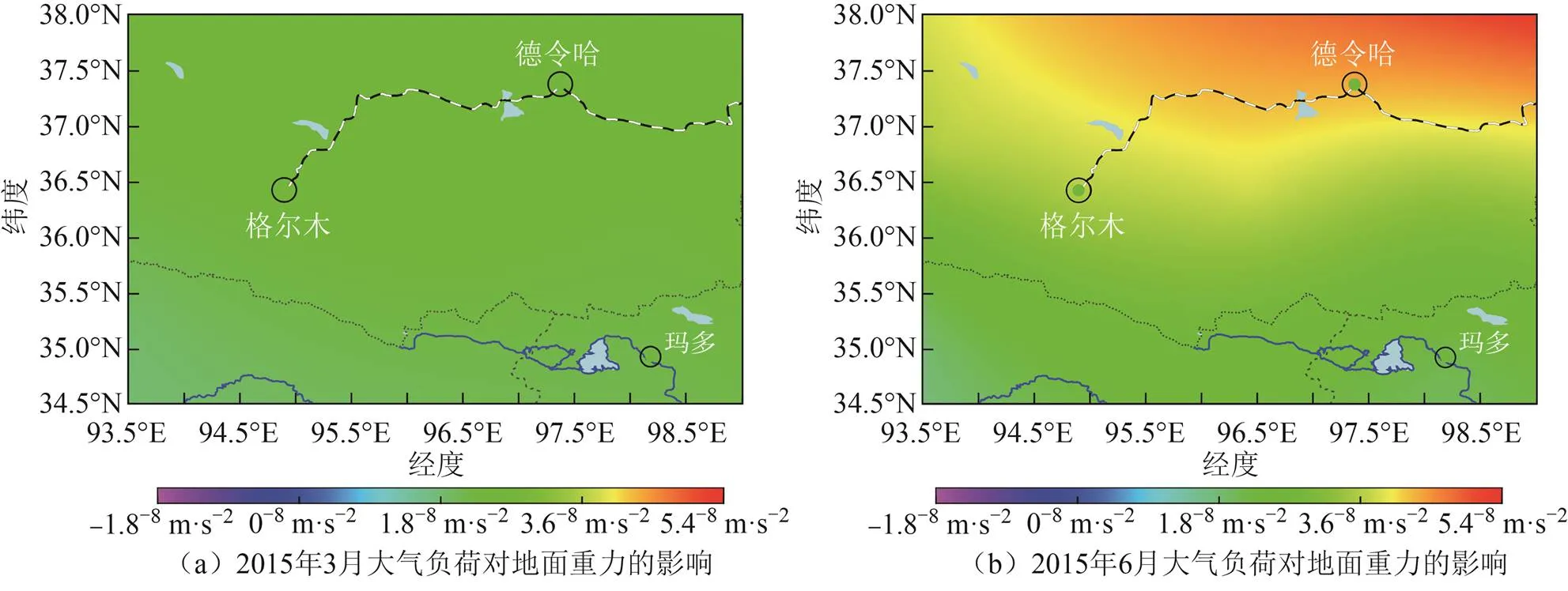
图3至图5所反映的周期性和季节性与研究区域周边地区(如新疆地区)的变化规律[16]具有较高的一致性。
3.3 统计分析
表1统计了2012—2017年大气负荷对地壳形变及重力变化的标准差及年变化幅度信息,由于使用标准差统计方式不能完全揭示长周期占优势信号的变化特征,因此,本文在统计标准差的同时,也对其负荷影响的年变化幅度进行了统计。表1中的年变化幅度即为6年中对应负荷影响的最大值。

表1 大气负荷对各种形变的影响统计
注:水平形变只统计其模的大小
表1结果显示:大气负荷对三种类型的年变化幅度依次为8.4 mm、不足1.0 mm和6.4×10-8m·s-2。其中,大气负荷对垂直形变与地面重力的影响在2012—2017年间有减小的趋势,如2012年最大值为8.1 mm与6.4×10-8m·s-2,2017年减小到6.1 mm与4.8×10-8m·s-2。均值由3.9 mm和2.7×10-8m·s-2减小到2.5 mm和1.5×10-8m·s-2。这说明除了大气负荷这一影响因素外,还有其他因素(如土壤水、地下水等)也同样会造成地壳形变与地面重力的变化,从而导致其形变量与变化量出现逐年减小的趋势,具体原因有待进一步分析。
本文选取了区域内QHGE(青海格尔木)与QHMD(青海玛多)两个具有代表性的连续运行参考站(continuously operating reference stations,CORS)的数据,并将其形变量及变化量内插至CORS站点,结果如图6、图7所示。
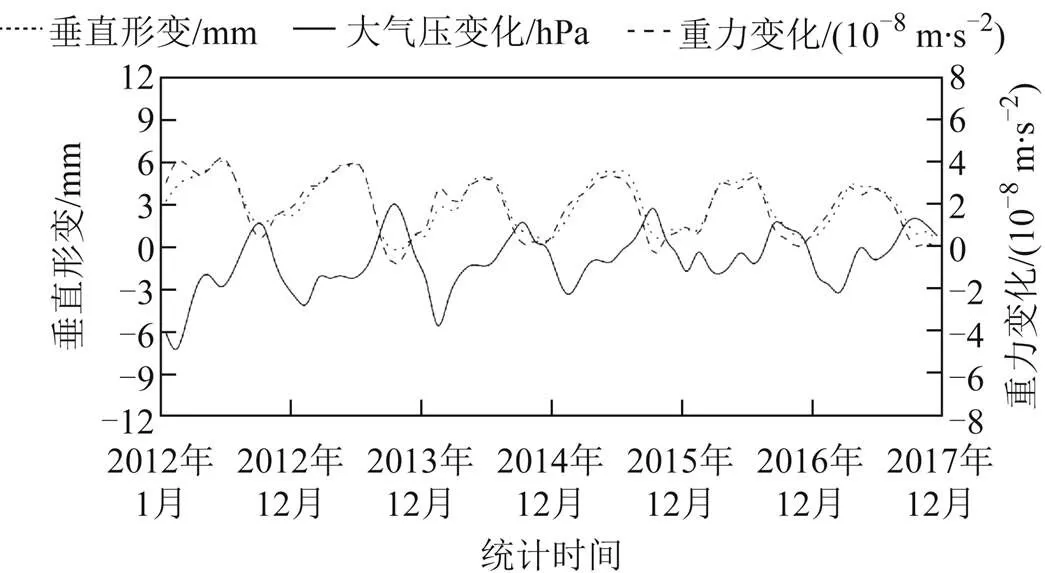
图6 QHGE站点大气压变化、垂直形变和重力变化
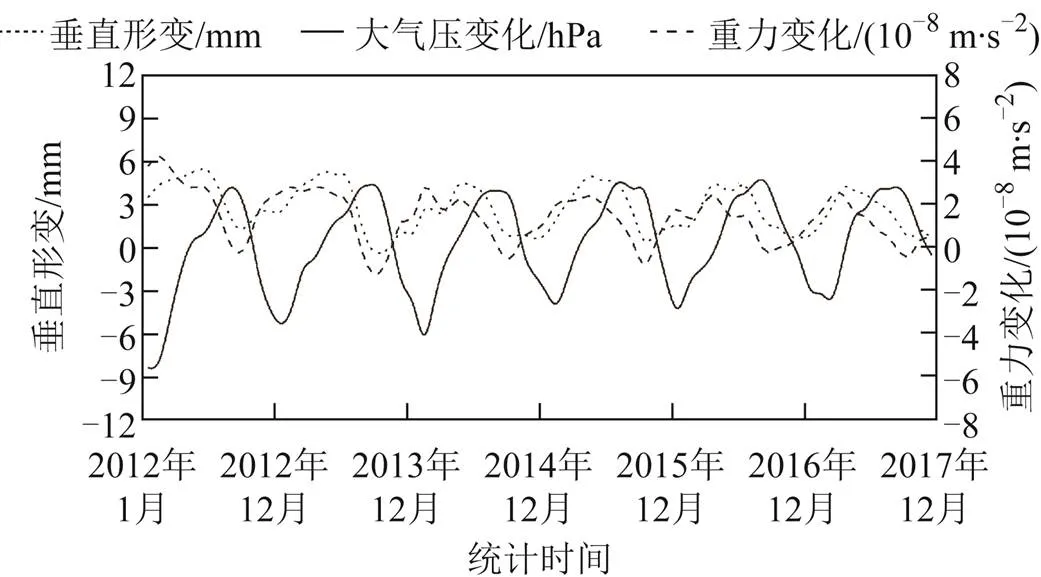
图7 QHMD站点大气压变化、垂直形变和重力变化
由图6,图7可知,点形虚线和线型虚线代表的垂直形变及重力变化有明显的周期性。例如,两种线型所代表的的形变类型除2012年以外,都是以每年先增大后减小,随时间而变化。另外还具有季节性变化规律,大气负荷影响在每年春夏季最大,秋冬季最小。以QHGE站点为例,负荷形变春夏季增大的速度较慢,在6月份左右到达最大值,秋冬季减小的速度较快,在9月份左右到达最小值。反观QHMD站点的重力变化曲线,2015年、2016年和2017年的峰值提前到3月份左右,这可能与该站点一定范围内的土壤水及地下水含量变化有关。纵观整体形变规律,与中国大陆地区的气候特征有明显的联系。同时可以发现随着时间的推移,形变负荷的年变化幅度有所减小。
4 结束语
本文采用移去恢复法,在全球大气压数据的基础上,结合祁连山南麓区域气象站实测大气压数据,计算了区域内地壳形变及重力变化的负荷效应影响特征。结果表明,大气负荷具有年周期性以及季节性的变化特征。垂直形变的年幅度影响为8.4 mm左右;水平形变的影响不足1.0 mm。重力变化的年幅度影响最大为6.4×10-8m·s-2,且与大气压变化成负相关。大气负荷的季节性表现为:春夏季达到最大值,其增大趋势较为缓慢;秋冬季达到最小值,其减小趋势较快。此结论与周边区域的地壳动力学在变化范围及影响特征具有较高的一致性。综合6年的负荷形变可以发现,年变化幅度影响有所减小。本文的方法如果应用到富含水体的区域时,则需要在球谐系数基础上考虑潮汐调和常数的计算。
[1] 王伟, 党亚民, 章传银, 等. 基于 CORS 站网监测三峡地区陆地水负荷对地壳形变和重力变化的影响[J]. 地球物理学报, 2017, 60(3): 962-971.
[2] FARRELL W E. Deformation of the Earth by surface loads[J]. Rev Reviews of Geophysics & Space Physics, 1972, 10(3): 761-797.
[3] JEAN-PAUL B, PASCAL G, JACQUES H. Reduction of surface gravity data from global atmospheric pressure loading[J]. Geophysical Journal International, 2002, 149(2): 534-545.
[4] 张诗玉, 钟敏, 唐诗华. 我国GPS基准站地壳垂直形变的大气负荷效应[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1090-1093.
[5] LONGMAN I M. A Green’s function for determining the deformation of the Earth under surface mass loads: computations and numerical results[J]. Journal of Geophysical Research, 1963, 68(2): 485-496.
[6] SPRATT R S. Modeling the effect of atmospheric pressure variations on gravity[J]. Geophysical Journal International, 2010, 71(1): 173-186.
[7] MANGIAROTTI S, CAZENAVE A, SOUDARIN L, et al. Annual vertical crustal motions predicted from surface mass redistribution and observed by space geodesy[J]. Journal of Geophysical Research: Solid Earth, 2001, 106(B3): 4277-4292.
[8] MITROVICA J X, DAVIS J L, SHAPIRO I I. A spectral formalism for computing three-dimensional deformations due to surface loads: present-day glacial isostatic adjustment[J]. Journal of Geophysical Research: Solid Earth, 1994, 99(B4): 7075-7101.
[9] VANDAM T M, BLEWITT G, HELFIN M B. Atmospheric pressure loading effects on global positioning system coordinate determinations[J]. Journal of Geophysical Research, 1994, 99(B12): 23939-23950.
[10] 章传银, 李爱勤, 党亚民, 等. CORS 网区域重力场变化与地面稳定性跟踪监测方法[J]. 测绘科学, 2019, 44(6): 29-36.
[11] WU Xiaoping, HELFIN M B, IVINS E R, et al. Seasonal and interannual global surface mass variations from multisatellite geodetic data[J]. Journal of Geophysical Research, 2006, 111(B9): B09401.
[12] 刘宇, 李爱勤, 俞志强, 等. 大气负荷效应对浙江地区的影响分析[J]. 大地测量与地球动力学, 2020, 40(6): 591-595.
[13] 杨成生, 张勤, 李振洪. ECMWF 资料的边界层伸缩水汽加密算法[J]. 武汉大学学报(信息科学版), 2015, 40(1): 83-89.
[14] 孟现勇, 王浩, 雷晓辉, 等. 基于 CMDAS 驱动 SWAT 模式的精博河流域水文相关分量模拟、验证及分析[J]. 生态学报, 2017, 37(21): 7114-7127.
[15] RAY R D, PONTE R M. Barometric tides from ECMWF operational analyses[J]. Annales Geophysicae, 2003, 21(8): 1897-1910.
[16] 王海涛, 王斌, 王伟, 等. 大气负荷对新疆地区地壳形变和地面重力变化的影响[J]. 大地测量与地球动力学, 2019, 39(2): 189-194.
Study on the dynamical effects of atmospheric load on the southern foot of Qilian Mountains
AN Xuwei1,2, YANG Guolin1, SUN Xuexian3, LIU Tao1, ZHANG Bo1,2
(1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China;2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China;3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China)
At present, domestic researches on changes in surface characteristics of atmospheric loading effects was mainly concentrated in the southeastern coastal areas, while the study's researches in northwest plateau were poor. So this paper presented an improvement method: the global atmospheric model and regional atmospheric pressure data were used to improve the accuracy of local atmospheric load, calculated the impact of atmospheric pressure loading on crustal deformation and gravity changes in the southern piedmont of Qilian Mountains. Statistical analysis results showed that: the impact of atmospheric loading is mainly reflected in vertical deformation and ground gravity changes, and the impact of maximum annual magnitude is 8.4 mm and 6.4×10-8m/s2, while horizontal deformation is less than 1.0 mm. The atmospheric loading has obvious annual periodicity and seasonality, at the same time, this change law is consistent with the surrounding areas. However this method needs to consider calculation of the tidal harmonic constant if the method is applied to waterrich areas.
Spherical harmonic analysis; removal and restoration; Green's function; atmospheric admittance
P228
A
2095-4999(2021)02-0090-06
安旭伟,杨国林,孙学先,等. 祁连山南麓区域的大气负荷动力学效应研究[J]. 导航定位学报, 2021, 9(2): 90-95.(AN Xuwei, YANG Guolin, SUN Xuexian, et al. Study on the dynamical effects of atmospheric load on the southern foot of Qilian Mountains[J]. Journal of Navigation and Positioning, 2021, 9(2): 90-95.)
10.16547/j.cnki.10-1096.20210214.
2020-07-27
国家重点研发计划课题项目(2016YFC0803106);国家自然科学基金项目(41764001,41761088);兰州交通大学优秀平台支持项目(201806);兰州交通大学天佑创新团队项目(TY202001)。
安旭伟(1995—),男,甘肃平凉人,硕士研究生,研究方向为大地测量数据处理。
杨国林(1978—),男,甘肃定西人,博士,副教授,研究方向为大地测量理论及数据处理。
