延迟退休、隔代教养与企业年金缴费率∗

于文广 李 倩 王 琦

(1.山东财经大学保险学院 山东济南 250014)

(2.山东财经大学经济学院 山东济南 250014)

(3.山东财经大学数学与数量经济学院 山东济南 250014)

一、引言

随着中国经济的发展，中国养老保险制度不断完善，作为养老体系的第二大支柱，企业年金制度也在近几年得到了长足发展。我国企业年金制度的发展，源于20 世纪90年代的企业补充养老保险，2018 年2 月1 日，《企业年金办法》 (以下简称《办法》) 正式开始实施。《办法》 明确提出了“完善企业年金制度，建立多层次的养老保险制度”。经过近三十年的发展，企业年金制度通过提高员工素质等机制显著提升了中国企业的生产率(于新亮等，2017)。通过企业年金基金平衡模型，刘昌平(2005) 发现延迟退休会提高企业年金的替代率，并据此给出了不同情况下企业年金的给付方案。还有一部分学者肯定了税收优惠政策，提出将税收优惠政策与企业年金制度相结合，以促进企业年金制度的发展(刘云龙，2002)，建议在宏观调控下实行个税递延商业养老保险，并调整基本养老保险缴费率。

根据2019 年《中国统计年鉴》 可知，我国65 岁以上人口占比为11.9%，老年抚养比达16.8%，中国老龄化日趋严重，延迟退休问题已成为当前公众关注的社会焦点话题。延迟退休政策的制定需要考虑预期寿命延长等因素，景鹏和郑伟 (2020)、姚海祥(2018) 分别从预期寿命增加对经济增长和养老金收支平衡带来负效应的角度分析，验证了延迟退休政策的正向作用机制。另外，通过构建不同的OLG 模型，部分文献考察了延迟退休年龄对代表性个体以及经济变量的作用机制，肯定了延迟退休对经济发展以及人口出生率等带来的正向影响 (Boucekkine 等，2002；Mastrobuoni，2009，鲁元平等，2016；耿志祥和孙祁祥，2020)。高彦等(2017) 则运用OLG 模型评估降低缴费率及延迟退休的共同作用对经济的影响，发现只有共同实施降低基本养老保险缴费率政策和延迟退休政策，才能实现个人及社会效用的最大化。

与此同时，2016 年我国开始实行“二孩政策”，伴随年轻人工作压力的显著增加，隔代教养在现实生活中发挥着越来越重要的作用(Hank 和Buber，2009)。隔代教养不仅会对孙辈的成长产生影响，而且会提高老一代(祖辈) 的效用水平，改善祖辈的认知能力(Guzman，2004；Arpino 和Bordone，2014；Ahn 和Choi，2019)。于新亮等(2019) 从老年人领取新农保养老金角度进行分析发现，老年人参与隔代教养时间越长，领取新农保养老金提升其孙辈健康水平的作用越大。严成樑(2018) 和彭争呈等(2019) 通过研究发现，延迟退休与隔代教养之间存在挤出效应，且隔代照料时间提高会使中老年人劳动参与率下降。

通过对国内外相关文献进行回顾可知，OLG 模型是求解养老金最优缴费率、研究延迟退休政策等问题的一个常用方法，该模型从宏观经济出发，减少异质性特征带来的影响，同时OLG 模型通过分析代际财富转移，可以使结果更具参考价值。就目前研究而言，大部分研究都针对基本养老保险收支平衡或最优缴费率，对企业年金缴费率的研究少之又少，也未见有论文考虑隔代教养在此过程中的影响机制。随着企业年金制度的不断发展以及企业年金规模的不断扩大，企业年金缴费率的合理设定显得尤为重要，合理的企业年金缴费率应是在多方因素下共同决定的。基于以上原因，本文将在OLG 模型中引入隔代教养、延迟退休等因素，并将人口出生率内生，分析企业年金最优缴费率，从而使得研究结论更具有现实参考意义。

本文基于修正的OLG 模型，通过内生人口出生率，首先分析隔代教养和延迟退休对人口出生率的影响，其次考虑隔代教养以及延迟退休下企业年金最优缴费率问题，并由此讨论企业年金缴费率的变动对经济变量的影响。这主要是基于以下几个方面的考量:第一，延迟退休政策的实施必将对个人的终身效用、收入以及退休生活产生影响。企业年金作为一种养老保障制度，延迟退休将使企业年金的缴费期延长，个人在考虑其自身效用最大化以及合理的退休生活支出后，在工作期必然需要一个更加合理的企业年金缴费率。第二，随着二孩政策的实施以及工作压力的增加，祖父母对孙辈的照料也成了社会关注的热点，现有学者在研究中肯定了隔代教养对人口出生率的影响，人口出生率的变动也将影响个体在成年期的决策，从而影响其对企业年金的需求程度。综合以上两方面考虑，进一步考察延迟退休及隔代教养对企业年金最优缴费率的影响具有重要的现实和理论意义。

二、OLG 模型的设定

本文在前人研究的OLG 模型基础上，内生人口出生率，引入延迟退休、隔代教养等因素。同时为了简化模型，本文假定代表性个体同质且为理性人，企业处于完全竞争状态，经济中存在现收现付制的基本养老保险以及企业年金。

(一) 个人决策

代表性个体的经济生活包括成年期和老年期，每期30 年时间禀赋都为1，所有代表性个体都会存活到老年期，人口增长率等于当期子女的数量即nt＝Lt＋1/Lt，其中Lt和Lt＋1分别为第t期和t＋1 期处于成年期的人数。成年期个体通过工作获得工资收入，并将收入所得用于消费、储蓄和缴纳企业年金。基于本文延迟退休的设定，老年期个体要继续工作一定时间，其消费来源于储蓄、基本养老保险、企业年金账户以及延迟退休的工资收入。

成年期消费C1，t、老年期消费C2，t＋1及总效用水平U可以由以下公式表示:

其中，φ为代表性个体老年期的生存时间(0 ＜φ≤1)，x(0 ＜x＜φ) 为老年期的工作时间，本文将延迟退休设定为老年期工作时间的增加，即x增加。μ为老年期效用贴现因子，θ表示代表性个体对子女的偏好，θ越大则其更加注重子女数量，rt＋1代表利率水平，It＋1为代表性个体在退休后可获得的企业年金，St表示储蓄，wt表示工资水平，τ为企业年金缴费率。①现有政策对企业年金实行累积制，且将个人与企业缴纳的部分共同计入个人账户。考虑到企业缴纳部分在计算中的复杂性，本文设定将企业缴纳的部分转移给个人，企业仅承担现收现付制的基本养老保险。同时，从模型设定来看，基本养老保险个人累积部分与企业年金的设定相同，因此，本文中的τ 为总的企业年金缴费率与个人养老保险缴费率(8%) 之和。借鉴严成樑(2018) 的设定和结论，延迟退休对隔代教养时间有负效应，t期老年人的隔代教养时间设定为d(φ-x)，其中d表示老年人隔代教养参与度，(φ-x) 表示延迟退休对隔代教养时间的挤出效应，t期每个成年人能够获得的隔代教养时间为d(φ-x)Lt-1/Lt＝d(φ-x)/nt-1，故代表性个体在成年期参加工作的实际时间禀赋为1 -(vnt-d(φ-x)/nt-1) ＝Tt，其中v表示教养子女的单位时间成本，Pt＋1表示t＋1 期单位时间内的养老金，(φ-x)Pt＋1表示个人退休后获得的基本养老保险收入。

个体通过选择储蓄、子女的数量实现自身效用最大化，我们构造拉格朗日函数，在两期消费式(1) 和式(2) 的约束下，求解总效用式(3) 最大化的一阶条件，可得

由式(4) 可知，1 单位成年期的消费等价于μφ(1 ＋rt＋1) 单位老年期的消费。同时由式(5) 和式(6) 可得，储蓄水平和人口出生率依赖于多个方面共同的作用。

(二) 企业

我们设定企业处于完全竞争市场，生产的产品同质且规模报酬不变，生产函数采用柯布-道格拉斯生产函数，则生产函数表示为:

其中，A代表综合技术水平，Nt＝TtLt＋xLt-1代表t期的劳动力人数，Kt代表t期企业的资本投入，α(0 ＜α＜1) 为资本收入。

假设企业在完全竞争市场中运营，物质资本在一期内完全折旧，使用资本达到边际产出rt，雇佣劳动力达到边际报酬wt，同时企业按照一定比例η缴纳基本养老保险，则企业利润最大化的条件可以由以下关系式表示:

(三) 政府

政府的职能分为两部分:监督管理企业年金账户，并保证基本养老保险账户收支平衡。借鉴Miyazaki (2014) 的思路，本文假定基本养老保险为现收现付制，缴费率为η，t期工作的人缴纳的基本养老保险分配给当期已经退休的老年人，对应如下基本养老保险收支方程:

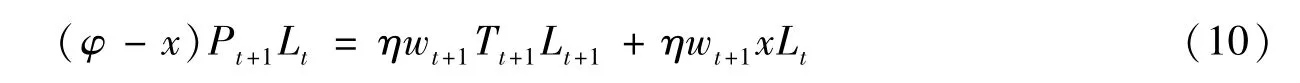
等式左边表示基本养老保险账户支出，等式右边表示基本养老保险总账户收入。

本文将企业年金设定为完全累积制，代表性个体的企业年金缴费率设定为τ并在退休后获取全部企业年金，则代表性个体获得的企业年金可以表示为:

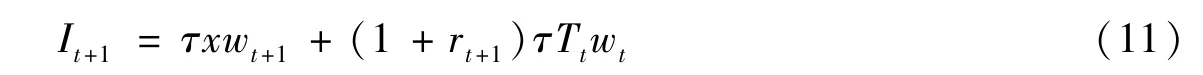
其中，企业年金作为经济体系中资本的一部分，其收益率应与储蓄的收益率相等。

(四) 资本市场

假定资本市场出清，根据本文设定，当期的资本积累来自于代表性个体的储蓄以及缴纳的企业年金，并全部用于下一期的资本投资，则资本积累的动态方程为:

将式(12) 两边同时除以t＋1 期的劳动供给Nt＋1，则t＋1 期的劳均资本可表示为:

三、均衡分析

在新古典增长框架下，不考虑外生技术进步，当经济收敛到均衡状态即满足kt＋1＝kt＝k∗、nt＋1＝nt＝n∗时，有稳定的唯一解。将上述条件代入式(6) 和式(13) 中，可得到均衡状态下劳均资本k∗和生育率n∗满足的条件:

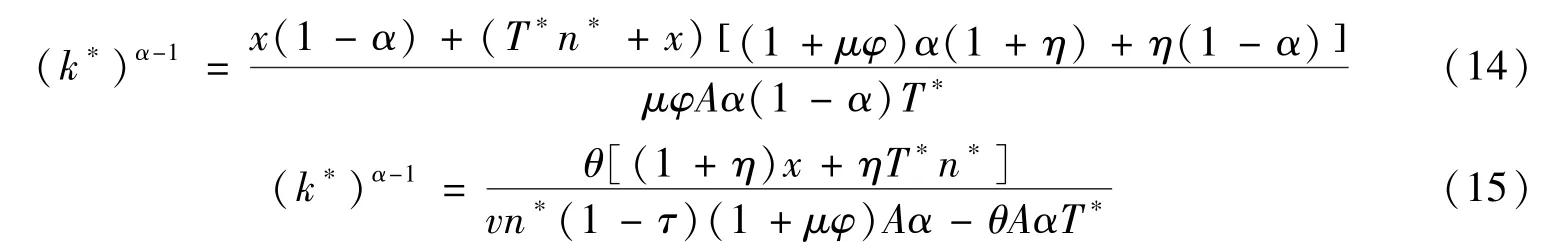
根据式(14) 和式(15)，均衡状态下劳均资本k∗和出生率n∗是关于延迟退休x和隔代教养参与度d的函数。借鉴严成樑(2016) 的分析思路，我们通过图形方法分析延迟退休和隔代教养对均衡状态内生变量的影响。将式(14) 的分子分母同除以T∗发现，(k∗)α-1随n∗的增加而严格递增；将式(15) 的分子分母同除以n∗发现，(k∗)α-1随n∗的增加而严格递减。综上可得，均衡状态下(k∗，n∗) 是唯一确定的，具体关系如图1 所示。

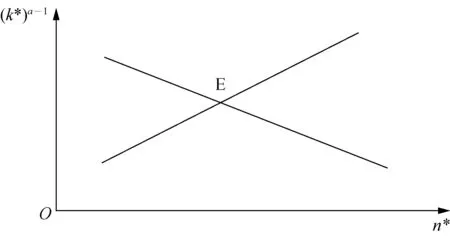
图1 均衡状态下的劳均资本和出生率

进一步分析延迟退休x和隔代教养参与度d变动对均衡状态(k∗，n∗) 的影响。将式(14) 和式(15) 等号右边分别定义为P(d，x，n∗) 和Q(d，x，n∗)，则有

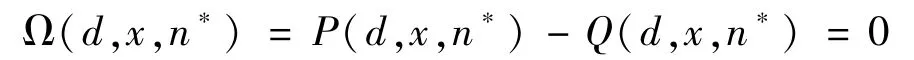
根据隐函数定理:

借鉴严成樑 (2016) 的方法，通过计算可得sign(dn∗/dx) ＞0，这与严成樑(2016)、景鹏和郑伟(2020) 的结论相同，即延迟退休会使均衡状态下的人口出生率上升。这可以从两个方面来解释:一方面，延迟退休意味着老年期的收入增加，代表性个体将减少其在成年期的储蓄水平，即选择更少的工作时间，教养孩子的时间禀赋提高，使得人口出生率上升；另一方面，延迟退休使资本存量减少，工资水平将下降，代表性个体为了实现其效用水平，将减少抚育子女的时间转为努力工作，导致人口出生率下降。在本文的设定下，延迟退休对人口出生率的正向作用大于其负向作用，推迟退休年龄会使人口出生率上升。

同理，sign(dn∗/dd) ＞0，则在现收现付制基本养老保险和企业年金的体系下，隔代教养参与度d的增加将提高人口出生率n∗，原因在于随着隔代教养参与度的增加，老年人用于教养孙辈的时间增加，意味着成年期的个体时间禀赋增加，人口出生率将上升；另一方面，隔代教养参与度的增加对劳均资本有负向作用，代表性个体的工资收入将下降，代表性个体需要投入更多的时间禀赋才可以满足储蓄和日常消费，其教养孩子的时间将下降，对人口出生率产生负效应。综合两方面因素可知，隔代教养参与度对人口出生率的正向作用大于负向作用，即隔代教养参与度的提高会使人口出生率上升。

四、企业年金最优缴费率

本部分从社会福利最大化角度出发，计算最优企业年金缴费率。沿用杨再贵(2010)、康传坤和楚天舒(2014) 的思路，首先求解满足社会福利最大化的劳均资本水平，其次将稳态下的劳均资本方程与社会福利最大化下的劳均资本水平联立，即可求解企业年金最优缴费率。

首先，构造社会福利函数。将社会福利函数定义为从0 期开始无限存续的个人效用函数的加总，定义ε(0 ＜ε＜1) 为社会效用贴现率，表示政府对各代人效用的重视程度，C0，t表示0 期老年人的消费，则社会福利函数的方程为:

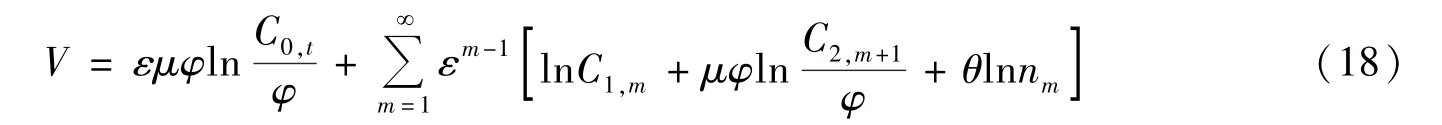
其次，资源约束条件。每一期的资源约束条件为当期的总产出与期初资本存量的加总，则t期的资源约束为:

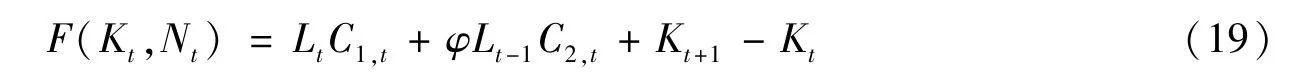
最后，通过构造拉格朗日方程，在给定初始条件k0的情况下，政府为了实现社会福利最大化，求得劳均资本表达式为:

将式(20) 与式(15) 联立整理，即可求得社会福利最大化且经济处于稳态时企业年金最优缴费率τ的表达式:

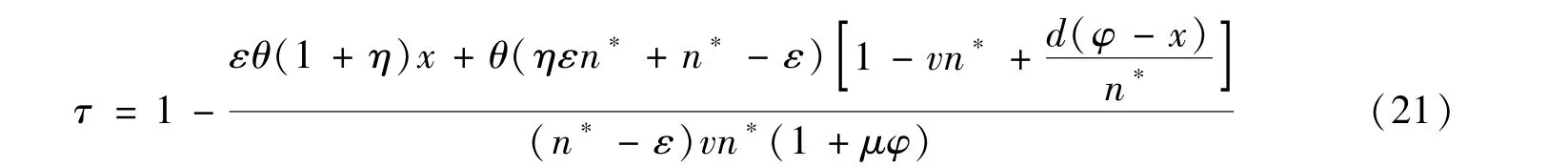
由式(21) 可得，企业年金最优缴费率τ受多方面因素共同影响，包括延迟退休的时间x、隔代教养参与度d以及教养孩子的时间v、子女数量偏好θ、人口增长率n∗、社会效用贴现因子ε、个人效用贴现因子μ、代表性个体人口预期寿命φ、基本养老保险缴费率η等，因此延迟退休年龄与隔代教养参与度的变化都将会影响最优企业年金缴费率。特别地，式(21) 中不包含代表综合技术水平的A，说明综合技术水平的改变对企业年金缴费率的变动不产生影响，原因在于当经济处于稳态均衡时，劳均资本、人口增长率都收敛为常数，此时经济增长率等于人口增长率，为一个常数，综合技术进步水平在其中不发挥作用。

五、赋值模拟与分析

(一) 基准参数设定

1.人口参数

预期寿命φ。根据《2018 年我国卫生健康事业发展统计公报》 对我国人口预期寿命的预测，结合实际情况，设定人口的预期寿命为78.5 岁，即老年期的时间禀赋为φ＝0.7833。

教养孩子的时间投入v。借鉴严成樑(2018) 的相关设定并结合目前我国父母对子女教育的重视程度，将成年期用于教养孩子的时间投入定为25%。

子女偏好θ。借鉴Fanti 和Gori (2012) 的参数设定，考虑到子女个数以及对父母的转移支付率的不断增加，将代表性个体对子女的偏好程度设为0.4。

2.经济参数

资本收入α。在本文的设定中，α的取值应不大于0.43，结合杨再贵(2010) 将资本收入设定为0.35，本文将资本收入α设定为0.3。

基本养老保险缴费率η。根据《国务院关于完善企业职工基本养老保险制度的决定》，同时结合本文的实际情况，将企业缴纳的基本养老保险缴费率设定为16%。

综合技术水平A。现有文献对综合技术水平的估算有一定的差异，本文借鉴康传坤和楚天舒(2014) 的设定，取2.5%作为年度全要素生产率增长率，则A的取值为2.05。

3.贴现参数

社会效用贴现率ε。社会效用贴现率表示政府对不同代人的重视程度，ε越接近1 意味着政府越重视后人的效用水平。本文借鉴康传坤和楚天舒(2014) 的取值，将社会效用贴现率设定为ε＝0.4845。

个人效用贴现率μ。参考Buiter (1981) 对时间贴现率的定义，个人效用贴现率的公式为μ＝1/[(1 ＋γ)φ]。考虑到时间贴现率小于实际利率，本文参考康传坤和楚天舒(2014) 的取值，将年度时间贴现率设定为0.01，则γ＝0.3345，本文的个人效用贴现率μ＝0.9567。

4.变量参数

隔代教养参与度d。依照现有研究，严成樑(2018) 认为在延迟退休前提下，隔代教养时间取值范围为[0，0，3]，结合目前中国隔代教养的实际情况，同时考虑本文的设定，为了分析隔代教养对企业年金缴费率变动的影响，本文假设隔代教养参与度取值范围为[0，0，2]。

延迟退休的时间x。根据中国现行的退休政策，本文初始退休年龄设定为55 岁。同时，依照本文设定，成年期在55 岁即退休时结束。根据“渐进式”退休政策，分别计算退休年龄在55—60 岁的情况，即x的取值为{1/30，1/15，1/10，2/15，1/6}。

表1 基准参数

(二) 企业年金最优缴费率

1.企业年金最优年缴费率计算

根据《企业年金办法》 规定，中国的企业年金最高缴费不得超过工资的12%，将表1中的基准参数代入式(21)，当不考虑延迟退休时(x＝0)，计算出τ的最优解为9.69%，则企业年金总最优缴费率为1.69%，即通过较低的企业年金缴费率就可以实现社会效用最大化，这也在一定程度上解释了我国现有退休制度下，企业年金发展较为缓慢的原因。

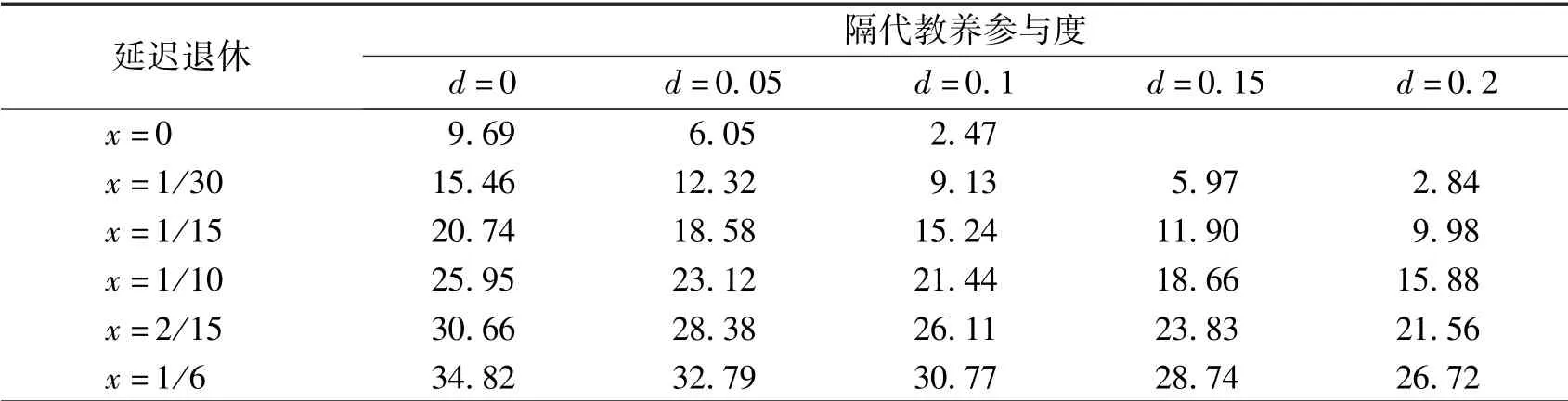
表2 企业年金最优缴费率 单位:%

表2 给出了不同隔代教养参与度下，退休年龄发生改变后相对应的企业年金最优缴费率。通过数值模拟结果发现，无论代表性个体用于隔代教养的时间有何改变，随着退休年龄的提高，企业年金最优缴费率均呈现上升趋势，出现这种结果可以从以下两个方面来解释。一方面延迟退休对企业年金缴费率有正向作用，第一，随着延迟退休年龄的增加，人口出生率会提高，劳均资本下降，工资水平也会下降，代表性个体为了实现效用最大化，无论是从自身收入角度，还是养育孩子角度来看，都会选择增加自己的企业年金，以保证退休后个人效用水平；第二，延迟退休年龄增加，意味着用于参与隔代教养的时间减少，代表性个体需要拿出更多的时间用于养育自己的子女从而导致其成年期的工作时间减少、收入下降，因此需要更高的企业年金缴费率才能使其老年期的收入满足其效用水平。另一方面，延迟退休意味着代表性个体老年期收入上升，促使代表性个体选择在成年期减少储蓄和企业年金水平，即延迟退休对企业年金缴费率有负向作用。通过研究发现，延迟退休对企业年金缴费率的正向作用大于其负向作用，即为了实现社会福利最大化，延迟退休年龄的同时需要对企业年金缴费率进行相应的调整。

表2 同时反映出隔代教养参与度能改变对企业年金缴费率的影响机制，随着隔代教养参与度的提高，企业年金缴费率呈现下降趋势。隔代教养参与度提高，处于老年期的代表性个体将会拿出更多的时间用于隔代教养，从而使成年期的子女有更多的时间用于工作并使收入增加，因此对企业年金缴费率有负向作用。同时，随着隔代教养参与度的提高，人口出生率上升，劳动人口数量也将上升，使得劳均资本下降并伴随工资下降，代表性个体为了实现其终身效用最大化，就需要提高企业年金缴费率，因此隔代教养参与度提高对企业年金缴费率有正向作用。综合两方面因素可知，隔代教养参与度对企业年金缴费率的负向作用大于其正向作用，即为了实现效用最大化，随着老年人参与隔代教养的程度提高，企业年金最优缴费率将逐渐下降。

模拟结果同时表明，隔代教养对企业年金缴费率的负向影响要小于延迟退休年龄带来的正向影响。第一，根据本文设定，2015 年出生的人最早会在2040 年参加工作，这会导致隔代教养对企业年金缴费率的影响有一定的滞后性。第二，由于延迟退休和隔代教养时间之间存在挤出效应，从老年个体身体健康等角度出发，退休年龄提高，用于隔代教养的时间必然会减少，在两方面共同作用下，企业年金缴费率终将呈现上升的趋势。

2.稳健性检验

根据式(21)，在社会福利最大化下，一般均衡状态同样取决于除延迟退休和隔代教养参与度之外的其他基准参数的合理性，同样，这些基准参数也会影响企业年金最优缴费率，因此我们对以下基准参数做敏感性分析，即资本产出弹性α、个人效用贴现因子μ、人口预期寿命φ、社会效用贴现因子ε以及子女偏好θ。为此我们以60 岁退休为基准，分析不同隔代教养参与度的情况，结果如表3 所示。

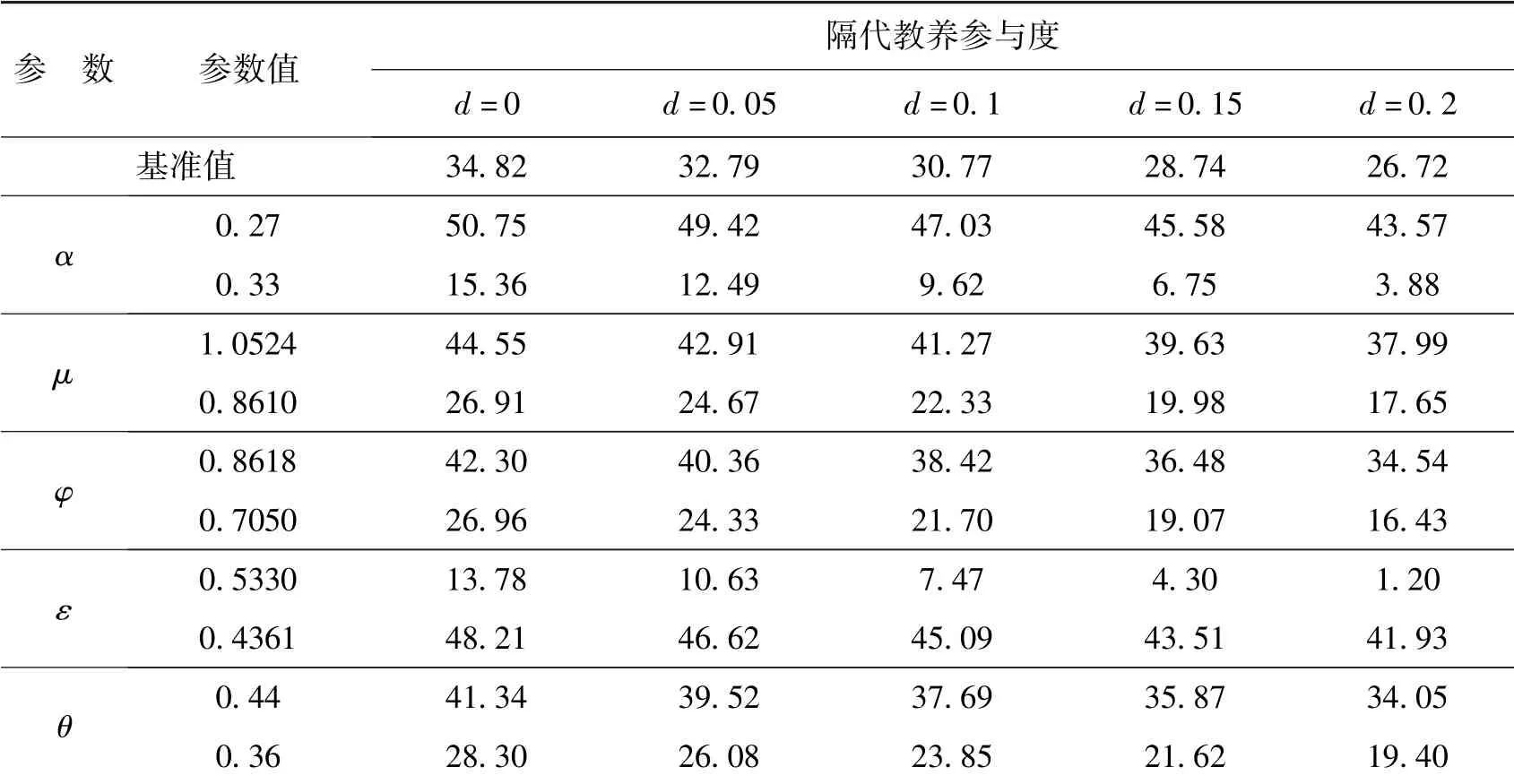
表3 企业年金最优缴费率稳健性分析 单位:%

从表3 可以看出，资本产出弹性α与企业年金最优缴费率呈反向变动关系，这与康传坤和楚天舒(2014) 的结论一致。α越高，意味着老年人的资本回报率越高，则较少的企业年金就可以保证退休后的生活消费水平。个人效用贴现因子μ与企业年金最优缴费率呈同向变动关系。μ越大，意味着代表性个体越看重退休后的生活水平，因而需要更高的企业年金缴费率。人口预期寿命φ与企业年金最优缴费率呈同向变动关系。φ越大，则代表性个体的预期寿命越长，需要较高的企业年金缴费率才能维持退休后的效用水平。社会效用贴现因子ε与企业年金最优缴费率呈反向变动关系。ε代表政府对年轻一代的重视程度，ε越大则政府越重视年轻人的效用水平，对企业年金缴费率产生负向影响。θ越大，则代表性个体越看重子女数量，其生育意愿会增加，人口出生率上升意味着成年期代表性个体的工作时间减少，为了实现老年期的效用最大化，就需要提高企业年金缴费率，即θ对企业年金缴费率有正向作用。表3 还显示企业年金最优缴费率τ∗受资本产出弹性α、个人效用贴现因子μ、人口预期寿命φ、社会效用贴现因子ε、子女数量θ等因素的影响，因此我们在决定τ∗之前，需要充分研究所选取的参数是否符合经济发展情况，只有设定合理的相关参数，才能得到最优的企业年金缴费率。

(三) 企业年金缴费率变动对经济的影响

以上分析了在社会福利最大化条件下，延迟退休和隔代教养的变化所对应的不同企业年金最优缴费率，意味着在制定延迟退休政策时需对企业年金缴费率做出相应的变动，才能保证社会福利最大化。企业年金作为资本积累的一部分，仅仅从延迟退休政策考虑降低企业年金缴费率明显是不够的，还要具体分析企业年金缴费率的变化会对经济变量带来怎样的影响。由于不同退休年龄和隔代教养参与度下企业年金缴费率的改变对经济变量的影响机制是相同的，因此本文主要分析退休年龄为60 岁、隔代教养参与度为0.2的情况下企业年金缴费率变动对经济变量的影响机制，其他基准参数同表1 中的设定。表4 给出了企业年金缴费率由30%降至15%时，劳均资本和生产要素价格的变动幅度及变动方向。

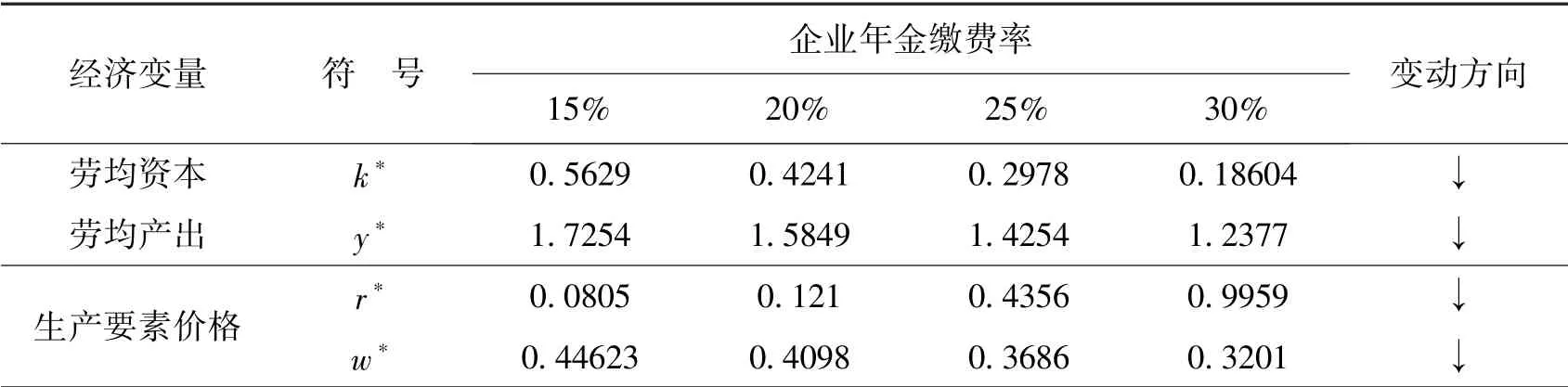
表4 降低企业年金缴费率的经济效应

表4 显示，企业年金缴费率变动对各经济变量的影响是不同的，企业年金缴费率与劳均资本和劳均产出呈现反向变动关系。随着企业年金缴费率上升，劳均资本和劳均产出呈现下降的趋势，根据模型公式，工资水平会随之降低，但是储蓄率会逐渐上升。

六、结论与启示

本文构造了一个包含隔代教养、延迟退休的OLG 模型，并在该模型框架下计算社会福利最大化前提下的企业年金最优缴费率，同时分析了延迟退休政策、代表性个体隔代教养参与度变化对企业年金最优缴费率的影响。研究表明，企业年金最优缴费率会随退休年龄的增加而提高，随隔代教养参与度的提高而下降。在选取基准参数后，计算可得现阶段我国企业年金最优缴费率为9.69%，当退休年龄为60 岁时，最优缴费率在26%可满足个人效用最大化。同时，企业年金缴费率变动也影响了经济水平，缴费率上升，劳均资本、劳动报酬都呈现下降趋势，资本使用成本上升。

考虑到中国正处于新旧动能转换期，经济下行压力较大，本文尝试综合考虑了退休年龄、隔代教养参与度、企业年金缴费率对经济带来的影响。通过数值模拟可以得出以下结论:第一，当经济处于均衡状态时，代表性个体增加对隔代教养的参与度会提高人口出生率，从而提高经济增长率以促进经济正常发展；第二，延迟退休年龄通过提高人口出生率、增加工作时间，有利于减轻人口老龄化对中国经济带来的冲击，从而可以抑制老龄化对中国经济带来的负向作用；第三，延迟退休年龄会使企业年金缴费率上升，提高基本养老保险和企业年金收入，缓解基本养老保险收不抵支的压力；第四，企业年金缴费率变动对经济变量的影响直接体现在劳动和资本使用成本，从而影响宏观经济发展。

企业年金最优缴费率的制定对中国经济发展、企业年金制度完善等都具有一定积极作用，政府在不断完善《企业年金制度》 的同时，应加强对企业年金的监管，企业也应根据自身的发展情况，制定符合自身实际情况的企业年金缴费率。在当前中国老龄化问题日益严重，以及人口红利逐渐下降的情形下，企业年金制度的发展和完善显得尤为重要。同时，企业年金作为养老保险的“第二支柱”，其良好发展有利于缓解基本养老保险收支不平衡问题，对提高养老保险替代率具有重要的意义。然而，从近几年中国企业年金的发展来看，只有小部分公司建立了企业年金制度，其大众认可度还不够高。同时，企业年金制度所提倡的税收优惠政策，实施效果也不是十分明显。为了提高企业年金制度作为补充养老手段的作用，借鉴美国、英国等国家的企业年金制度，应提高对企业年金的宣传力度，同时逐步完善税收优惠政策，从而提高企业年金基数水平，以实现企业年金“第二支柱”的作用，提高企业职工的终身效用水平。