基于全代引证的专利累积影响力评价——一个诺奖得主专利的案例研究

康旭东，邓乐乐，王宇开，杨中楷

（1. 大连理工大学技术研究开发院，大连 116024；2. 大连理工大学科学学与科技管理研究所，大连 116024）

1 引 言

继承性、发展性和积累性是技术创新活动中最显著的特点[1]，几乎所有的发明创造都是吸取前人的研究成果，继而消化吸收、总结拓展出新的创造性成果。专利作为技术创新的载体，专利之间的引用关系代表着技术之间的相互影响，施引可以反映相关的技术来源，而被引则表示本技术对后续技术发展的贡献。一般来说，专利的被引频次越高表示受其影响的后续技术越多，该专利涵盖的技术就越重要[2-3]。目前，已经有多数学者研究表明，直接被引频次可作为专利学术价值和技术影响力的测度。例如，国外学者Albert 等[4]研究发现，被引次数越高，专利价值和技术影响力越高；国内学者肖国华等[5]构建了基于被引频次的专利评价指标，用被引频次衡量专利的技术影响力，这意味着被引频次已经成为评价专利影响力比较公认的指标。

科学技术是一个积累过程，每个研究人员的成果本质上都是基于大量先前的工作，而不仅仅是直接引用的文献[6]。从专利引文网络来看，技术的进化和发展是连续的，在网络中纵横交错的每条 “引证链” 背后，知识在一代代继承和重组，技术在一代代创新和进步[7-8]。也许前后的专利技术差异很大，但是两者之间必然拥有内在的科学知识联系[9-10]。专利的影响力扩散绝不止步于一代引用关系，而是随着引用关系（间接引用）的增加不断传播和累积。虽然直接被引频次在一定程度上能够衡量专利影响力，但是 “一代” 的引用关系仅仅代表部分影响力，忽视了间接引用对专利影响力的贡献。因此，在衡量专利的影响力时，本研究有必要以累积影响力的视角，着眼于整个传播过程，而不是局限于一次的引用，既要考虑直接影响，又要考虑间接影响。

为了综合考虑直接引用和间接引用对技术影响力的贡献，国内外的学者们提出了一些具有代表性的方法。例如，Trajtenberg 等[11]考虑了两代引证关系，将直接被引权重设为1，而间接被引的权重设为0.5，用两代的加权累积被引次数来衡量专利质量高低；von Wartburg 等[12]认为更长的 “引用链” 才能获取更全面和准确的评价；Atallah 等[13]研究更深一步，综合考虑了全代引证和引证质量，计算全路径的累积被引频次，宏观上分析了不同领域的专利累积被引频次的差异以及年度变化趋势；胡小君[14]将 “引用代” 运用到评价科学影响力上，认为随着 “引用代” 的增加，专利的影响力应逐渐累积、增加；冯岭等[15]在评价专利价值方面采用一种 “潜在引用网络” ，通过利用专利文献的相似度构造引用关系，计算专利的累积价值。另外，PageRank算法也是学者们推崇的技术影响力评价方法，经过不断改进和完善，在实际应用中已取得了一定的效果[16-17]。

以往的研究大都只是在片面强调累积影响力的重要性，偏向宏观的统计描述分析，缺乏对专利累积影响力的差异原因、变化趋势等进行微观层次的详细阐述。虽然基于PageRank 算法的评价方法与影响力扩散密切相关，但是PageRank 算法依赖的是随机游走的权值计算方式，并不考虑技术起源和技术进化路径，也很难分析引文网络结构对累积影响力的影响。因此，本研究将从技术进化的角度，构建专利引文网络，分析影响力扩散路径，计算 “全代引证” 的累积影响力，力求更能够客观、全面的反映专利的技术贡献和学术价值。此外，本研究深度剖析专利引文网络的微观结构，展示引用过程逐渐复杂的变化轨迹，找出累积影响力的差异原因，并对累积影响力变化趋势做出尝试性预测。专利作为国家和企业的强有力竞争手段，把握核心影响力技术显得尤为重要，本研究为挖掘具有高影响力或高价值的技术提供方法指引。

2 数据来源和研究方法

2.1 样本选择

悉尼·布伦纳是公认的当代最伟大的生物学家之一，其研究涉及DNA 编码、基因测序、胚胎发育和生物进化，涵盖了整个现代生命科学领域。同时，布伦纳在职业研究过程中也申请了多项相关的专利，其不仅是一位顶尖科学家，更是一名高产的发明家。本文旨在研究专利的累积影响力，专利的技术影响力越高，即专利引证越多，研究结果就越准确。现有研究表明，生物领域中的专利引用行为较为频繁[18]，加上布伦纳本身作为诺奖得主，其申请专利的技术影响力较高，非常适合本文对专利累积影响力的研究。因此，本文选取悉尼·布伦纳申请的关于基因编码和遗传信息的全部授权专利，以此为研究素材，计算 “全代” 影响力，分析引文网络微观结构，挖掘专利累积影响力与引文网络的关联。

2.2 数据检索与处理

美国专利全文数据库拥有较为全面且权威的专利引文信息，便于研究人员对数据进行更深层次的加工分析，是众多学者研究专利引文的优先选择[19]。本文以美国专利数据库授权库中悉尼·布伦纳申请的相关专利为研究对象进行分析。

首先，获取所有目标专利。具体检索过程为：选取授权库（PatFT）→选取高级检索→输入检索式：IN/Brenner-Sydney （发明人/悉尼·布伦纳），检索时间为2019 年9 月1 日，经筛选共检索到有效专利91 个。由图1 可知悉尼·布伦纳授权专利年度分布情况，最早一篇专利是在1992 年授权，期间最多一年授权专利可达8 件，最终截止到2019 年。

图1 专利授权数量年度分布

其次，构建全库引证关系。理论上获取任何一个专利的全代引证关系，都需要获取美国专利数据库中全库的引文信息。本研究采用的是USPTO 提供的批量下载数据文件，其内部包含平台定期根据美国专利数据库中整理后的授权专利之间的引用关系。虽然与专利全文数据库的数据存在一定的时间差，但已能够满足研究人员使用。获取数据后，处理成一一对应的引用关系，以方便作进一步处理。

最后，获取目标专利的全代施引专利。获取全部的引用关系后，通过自编程迭代计算91 个目标专利的全部施引专利，计算结果的数据格式如表1所示。每一行代表一条完整的引证路径，每一列代表不同的引证代。其中，Gen0 表示目标专利US6352828，后续的Gen1、Gen2……Gen5 是每一代的施引专利，null 代表无施引专利。

2.3 影响力扩散模型与评价指标构建

分析影响力扩散过程是研究专利累积影响力的基础，而影响力的扩散与知识流动是密切相关。图2 为专利引用过程中知识流动与影响力的传播网络图，知识的流动是建立在引证关系之上，构建如图2a 所示的知识流动模型，目标专利P0 的总体知识流动方向依次为：第一代施引专利集合[Gen1]，第二代施引专利集合[Gen2]……到最后一代施引专利集合结束。具体来说，由图2a 可知，目标专利的知识是随着一条条 “引证链” 流向一代代施引专利的。专利之间知识的流动带来了技术之间的相互影响，因此，一个专利的影响力衡量应是基于知识流动的 “全代引证” 的累积结果，即把扩散到所有引证代（[Gen1]、[Gen2]、[Gen3]……）的影响力汇聚于目标专利本身。

本文通过知识流动模型构建如图2b 所示的影响力扩散网络图。构建影响力扩散模型有四个前提条件：①基于引用关系，构建引文网络，将专利文献作为节点，忽略专利内部包含的信息；②每个参考文献专利对其施引专利同等重要，即每条直接引用的影响力值记为 “1” ；③专利的影响力可以表示为其他专利影响值的加权总和；④随着引证路径的增长，引用关系对目标专利的影响力贡献逐渐减小。由图2b 可知， “0” 节点是目标专利，其影响力随着引用关系的增加在逐渐扩散，距离 “0” 越远的专利节点越小（颜色越淡），表示其受目标专利的影响越小；灰色节点代表非施引专利，即不受目标专利影响。网络中任何一个专利节点p的累积影响力可表示为其中，i∈表示专利p的全代引证（直接施引和间接施引）专利；αi表示影响力贡献权重；Ic表示每个引用的影响力值。

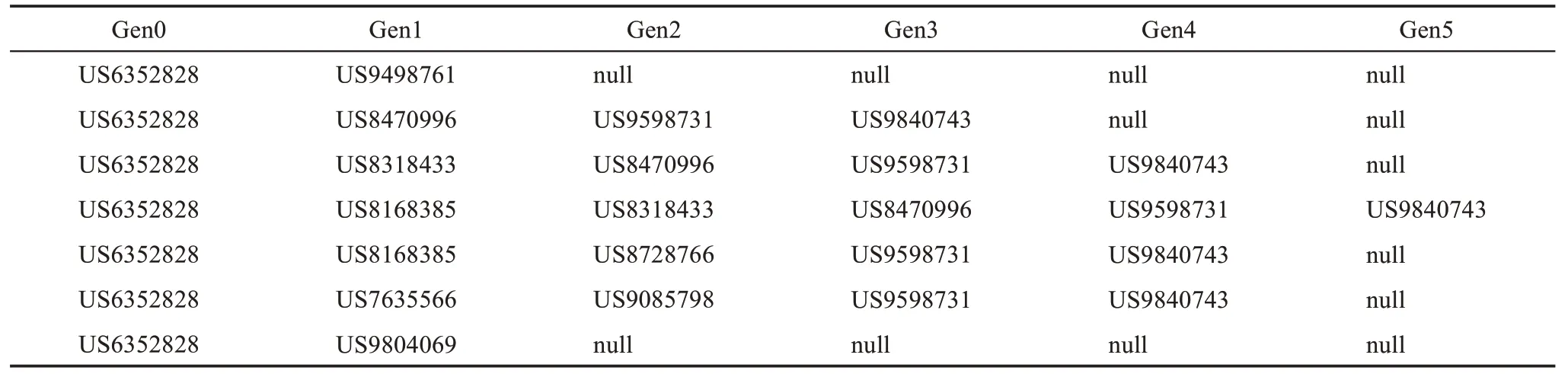
表1 专利US6352828全代施引专利计算结果

基于上述分析，借鉴Atallah 等[13]提出的基于全代引证的评价指标——累积引证频次，构建专利累积影响力评价指标。

首先，目标专利每代的被引频次计算公式：

其中，G表示引用代；N表示目标专利p前向引文网络中的全部专利；VG(p)表示目标专利p第G代的被引频次；V1(p)表示目标专利p的直接被引频次；QG-1(x)表示第G-1 代施引专利集合中的全部专利，当G=1 时，QG-1(x)为目标专利本身；δi(x)表示专利i是否引用专利x，如果引用，δi( )x为1，否则δi(x)为0。

进一步地，可以计算目标专利的全代引证频次：

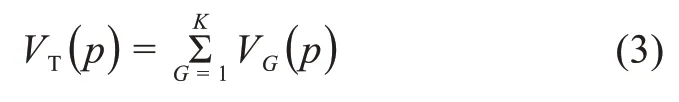
其中，K表示引证代；VG(p)表示每代的被引频次。

最后，得到加权累积引证频次，即累积影响力指数：

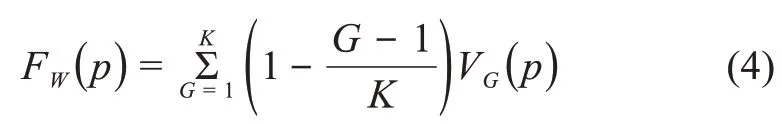
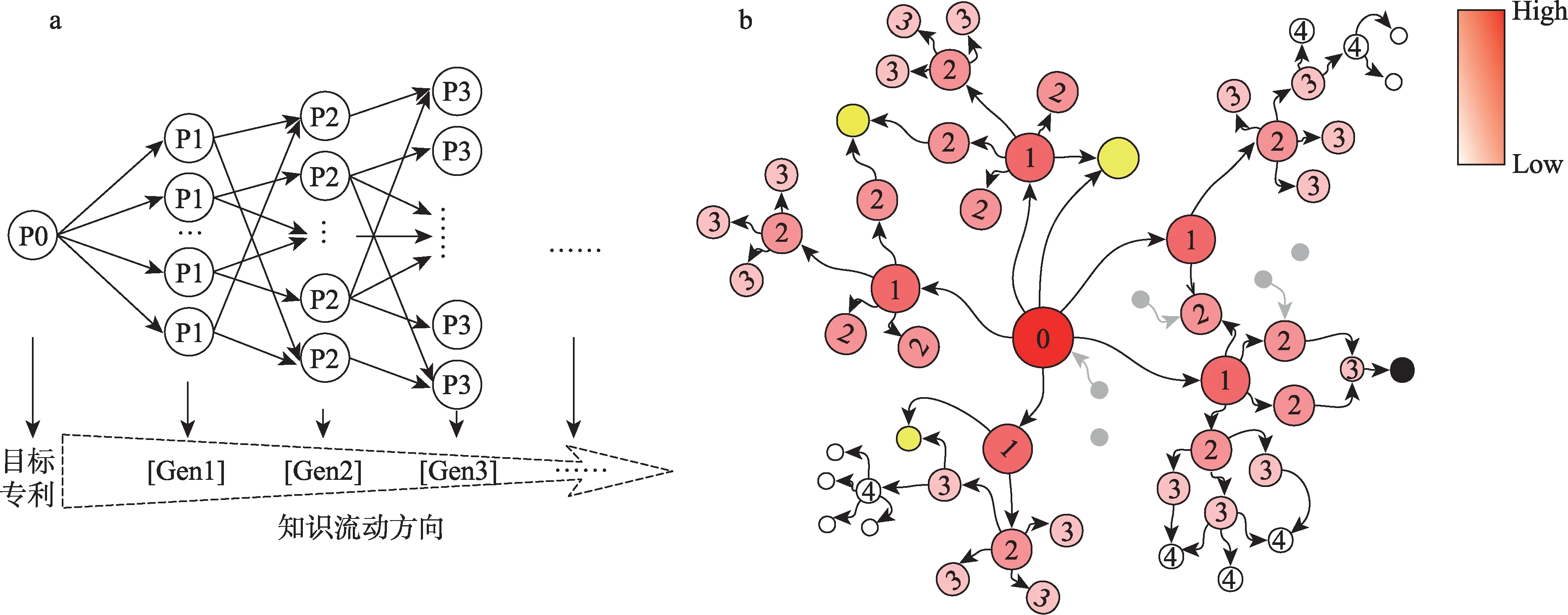
图2 专利知识流动与影响力传播示意图（彩图请见http://qbxb.istic.ac.cn/CN/volumn/home.shtml）

需要说明的是，不同路径中专利引用可能存在重复的情况。如图2b 中标出的黄色和黑色节点，其中黄色节点表示一个专利同时引用了不同的专利，是属于不同的引证关系；而黑色节点表示不同路径中相同的引证关系。但是，影响力贡献是基于不同的引证关系的，那么不管施引或被引的专利是否同代，本文都要把黄色节点的重复情况计算在内，而把黑色节点的重复情况删除。

3 直接被引频次与累积影响力指数的对比分析

3.1 基本信息描述

表2 为按照授权时间顺序排列前50 个目标专利的基本信息，从中可看出每个目标专利的授权年限、引证长度以及专利总数等详细信息。专利最早授权在1992 年，引证长度最长为20 代，专利总数最多为11856。总体来看，引证长度和专利总数都是随着专利授权时间的减少而减少，这是由于专利文献的引用存在时滞性[20]。一般来说，科学文献发表或者专利文献授权的时间越短，发生引用越少，导致引证长度和施引文献数越少。

值得注意的是，尽管总体上引证长度和专利总数随着授权时间减少，但是仍有个别专利的这两项指标与授权时间相同甚至更长的目标专利相比，明显高出很多，如表2 中第14 个专利US5763175 的专利总数和第20 个专利US5863722 的引证长度。根据影响力扩散模型可知，引证长度和专利总数越大，很大程度上说明了该专利的技术影响力传播和流动比较活跃，有理由推测这种类型的专利累积影响力更高。

表2 目标专利基本信息表

3.2 累积影响力指数的评价效力分析

根据处理后的数据以及公式(3)和公式(4)，计算得出所有目标专利的直接被引频次（V1）、累积影响力指数（FW）与全代引证频次（VT）。结果（前50） 如表3 所示，以累积影响力指数大小倒序排列，图3 为对应的折线趋势图（去除没有被引）。结合表3 和图3，本文发现一个基本规律：总体来看直接被引频次与累积影响力指数的变化趋势基本相同，侧面反映了累积影响力指数在专利影响力评价方面与直接被引频次相比具有同等效力。

此外，在图3 左侧累积影响力较高的区域，部分专利的直接被引频次相对偏低。观察表3 中排名前15 的专利，明显发现其中只有三个专利的直接被引频次大于100，大部分专利的直接被引频次都在40～60，最低的只有23。表2 中专利US5763175和专利US5863722，由于偏高的专利总数和引证长度，推测其在累积影响力上会有不错的表现，这在表3 中得到了充分的体现，两者的累积影响力不仅超过了授权时间更长的专利，甚至超过一些直接被引频次更高的专利。引证路径越长代表专利的知识流动越久远，专利总数越多说明专利的技术传播越广泛，这两种指标均是高影响力的体现，而直接被引频次却往往难以发现类似的专利，从而说明了累积影响力指数在专利影响力衡量方面具有更强的 “侦测” 能力。

然而，直接被引频次与累积影响力并不是毫无关系的。 表3 中的专利US5695934 和专利US5604097 累积影响力和直接被引频次都很高，结合表2 可知，两者的引证长度和专利总数与授权时间相近的专利相比都是明显比较高的。这说明尽管直接被引频次不能直接决定累积影响力的大小，但是更高的直接被引频次确实有更大的潜在被引证（间接）机会，产生更长的引证路径和更多的施引专利，进而间接影响专利的累积影响力。可以说，若直接被引频次高，则累积影响力可能很高；但是若累积影响力很高，则直接被引频次不一定高。

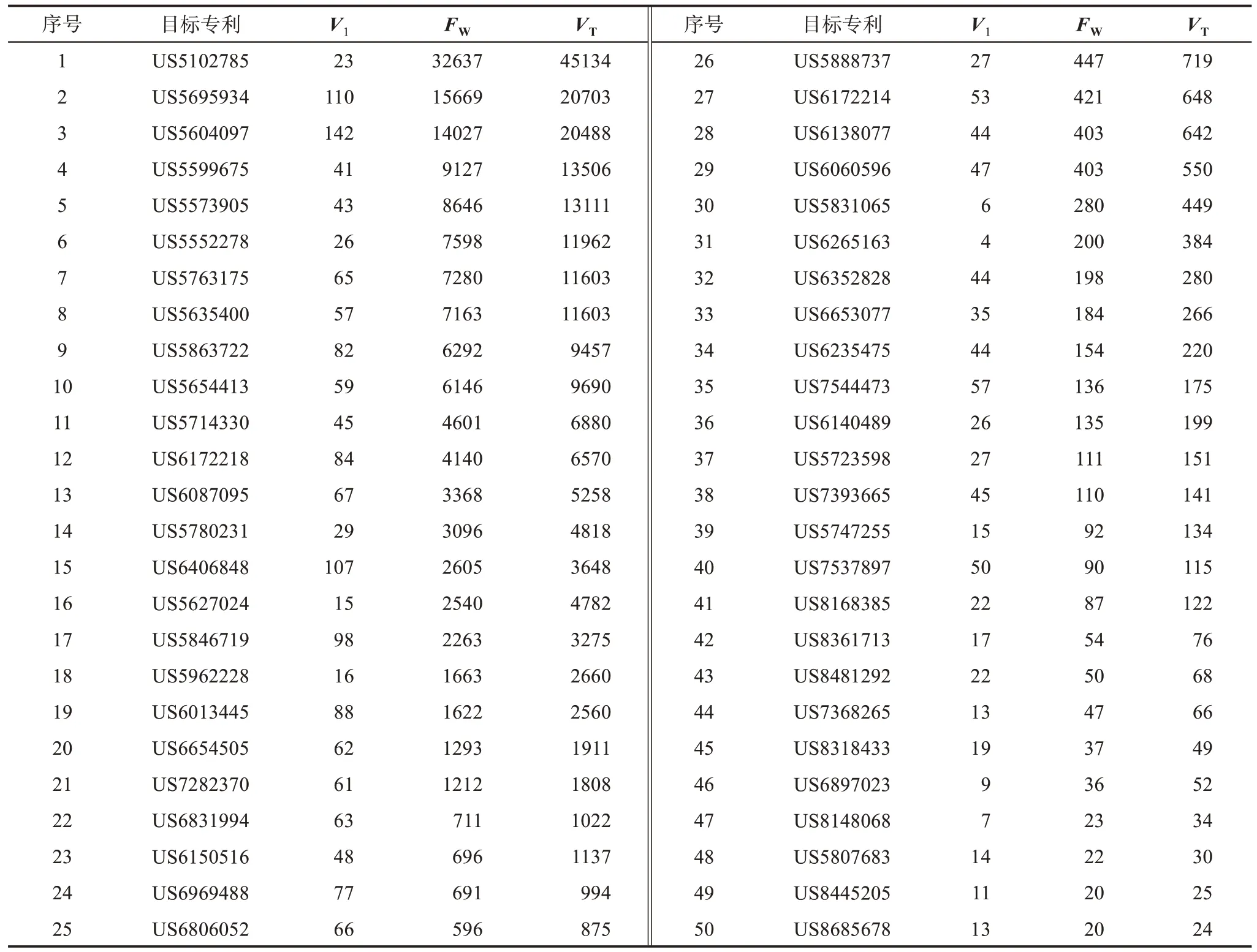
表3 直接被引频次与累积影响力指数对比表

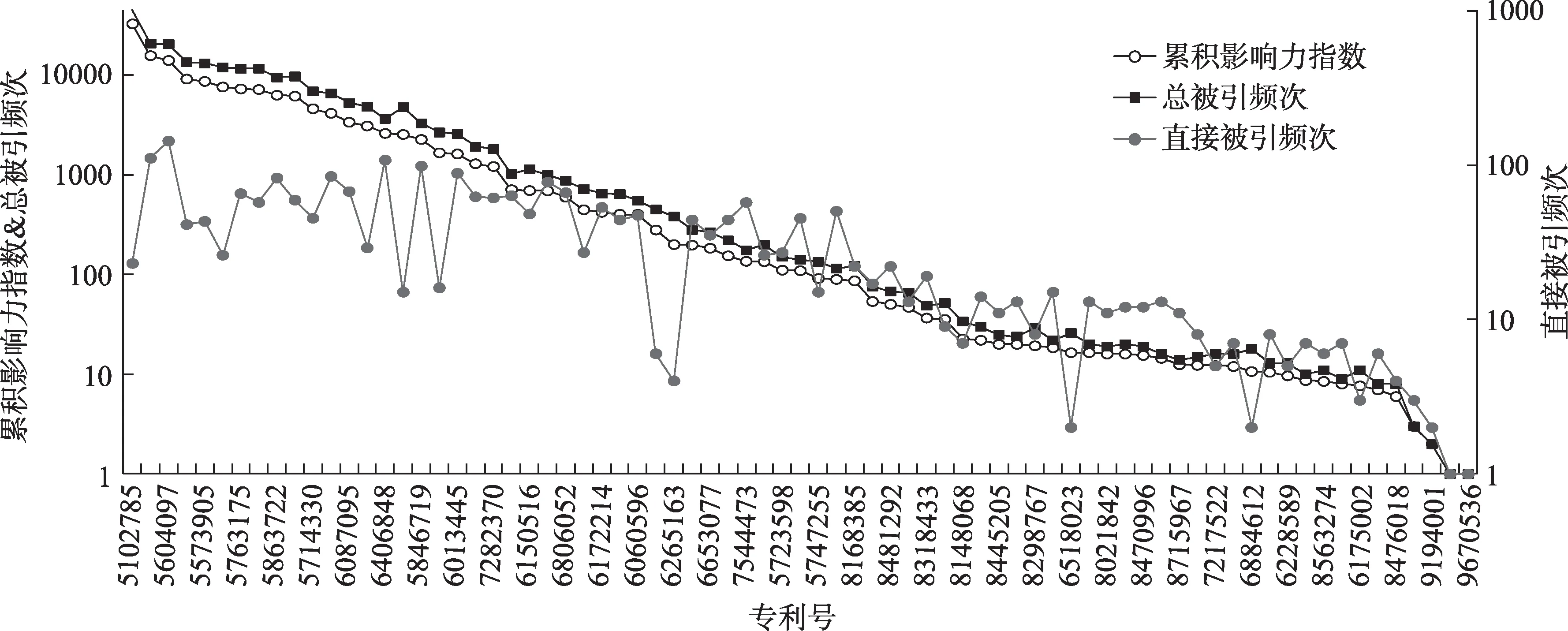
图3 直接被引频次与累积影响力指数的变化趋势

为了阐述直接被引频次与累积影响力指数的差异，更加体现累积影响力指数的优势和作用，本文结合案例作进一步详细分析。 表4 为专利US5780231 和专利US5723598 的各代被引频次以及施引专利数等详细信息。两专利在1998 年授权，可以忽略时滞性误差。如果只看直接被引频次（Gen1），可发现两个专利的情况差别不大，但是从第二代开始就发生了较大的转折，前者的后续引证频次和施引专利数比后者高出许多。 专利US5780231 持续引证到第8 代，而专利US5723598只被引证到第6 代，并且前者在第8 代依然有24 次被引和16 个施引专利，但后者逐渐为零。换句话说，专利US5780231 在未来仍有很大的可能性将会继续 “被引” ，引证链会继续增加。除此之外，专利US5780231 的施引专利总数为842， 是专利US5723598 的十倍还多，这说明受前者技术影响的专利量要高出后者甚多，这一结果在累积影响力指数上得到了充分的体现。

综上可知，累积影响力指数较好地综合了专利影响力扩散的 “广度” 和 “深度” ，能够较为全面和准确地评价一个专利的真实影响力。同时，与直接被引频次相比，累积影响力指数的专利影响力侦测 “灵敏度” 更高，能够深层次挖掘基于直接被引频次而忽略的专利影响力差距。

表4 专利US5780231和专利US5723598的各代被引情况

4 累积影响力指数的差异因素分析

随着专利数量的增加，专利之间已经形成具有一定规模的引用网络，极大地延伸了专利的引用过程，促进了专利之间的知识流动和扩散[21]。宏观层面，每个专利都处在一个完整的技术进化网络中；微观层面，每个专利都处在本身作为技术源的 “子网络” （前向引文网络）。一个专利的累积影响力大小与 “子网络” 息息相关，影响力的大小不仅决定了网络的生长速度与范围，而且时刻影响着网络的结构和复杂程度[22]。因此，为了分析不同专利累积影响力的差异原因，本文需要深入研究每个专利子网络的参数和微观结构。

4.1 专利子网络参数分析

在上文中已经讨论了累积影响力指数与引证长度、专利总数以及直接被引频次的关系。其中，引证长度是子网络中的最大引用路径长度，专利总数为子网络中所有的专利节点总数，直接被引频次为目标专利节点的出度。为了探究累积影响力指数与三个指标的具体关系，本文先将数据做归一化处理，将所有指标映射到区间[0,1]内，消除量纲差异，具体公式为图4 为上述四个指标的散点图，同时算出拟合曲线。

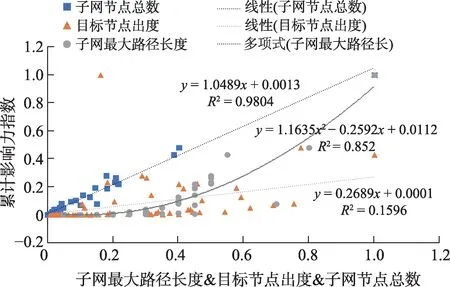
图4 累积影响力指数与子网络参数的散点图

从图4 可以看出，累积影响力指数与子网节点总数的线性关系最强，决定系数R2高达0.9804，说明了一个专利的影响力与受其影响的专利总数是线性相关的；子网最大路径长度与累积影响力指数呈二次函数关系，那么引证路径越长，影响力累积幅度越大；目标节点出度与累积影响力指数的线性关系较弱，说明只考虑直接被引频次不能准确把握一个专利的累计影响力变化趋势。

4.2 专利子网络各代引证结构分析

去除没有被引的目标专利，图5 为剩余75 个目标专利的各代被引频次分布图。从图5 可知，大部分专利的每代被引频次近似呈 “正态分布” 结构，峰值主要集中在第3 代（Gen3）和第5 代（Gen5）之间，也有个别出现在第8 代（Gen8）左右。峰值意味着当代被引频次达到最大值，根据前文的影响力传播理论：随着与目标专利距离越来越远，影响力的权重越来越小，那么峰值的大小和出现位置的不同很大程度上影响专利累积影响力的高低。如图5 标出的专利US5604097 和专利US5599675，前者的峰值更高且位置靠前，那么其累积影响力指数相对较高。一个专利的影响力扩散要看 “深度” 和 “广度” 两个层面，结合图5，横轴表示 “深度” ；纵轴表示 “广度” ，那么根据累积的思想，图5 中每一条曲线与横轴围成的面积可近似为目标专利的累积影响力。这也解释了专利US5102785 为何直接被引频次较低，却有远高于其他专利的累积影响力。

图6 为75 个目标专利的各代施引专利数量分布情况。对比图6 与图5 可以发现，两图非常相似，大部分的专利每代施引专利数量也近似呈 “正态分布” 结构，峰值分布区域也基本相同。各代施引专利数量与各代被引频次相似却又不同，虽然都能代表目标专利影响力扩散的速度，但与被引频次不同是，各代施引专利数更能代表目标专利的影响力扩散到不同专利的能力，简单来说，是对其他专利的 “吸引力” 。一个专利某一代的被引频次很高，并不代表这一代的施引专利很多，因为存在多个专利同时被一篇专利引用的情况，这导致在下一代可能仅有少数专利被引；而施引专利很多，则被引频次一定很高，同时也保证了下一代有更多的专利被引用。这也是图5 和图6 中曲线形状相似但值域相差较大的原因。

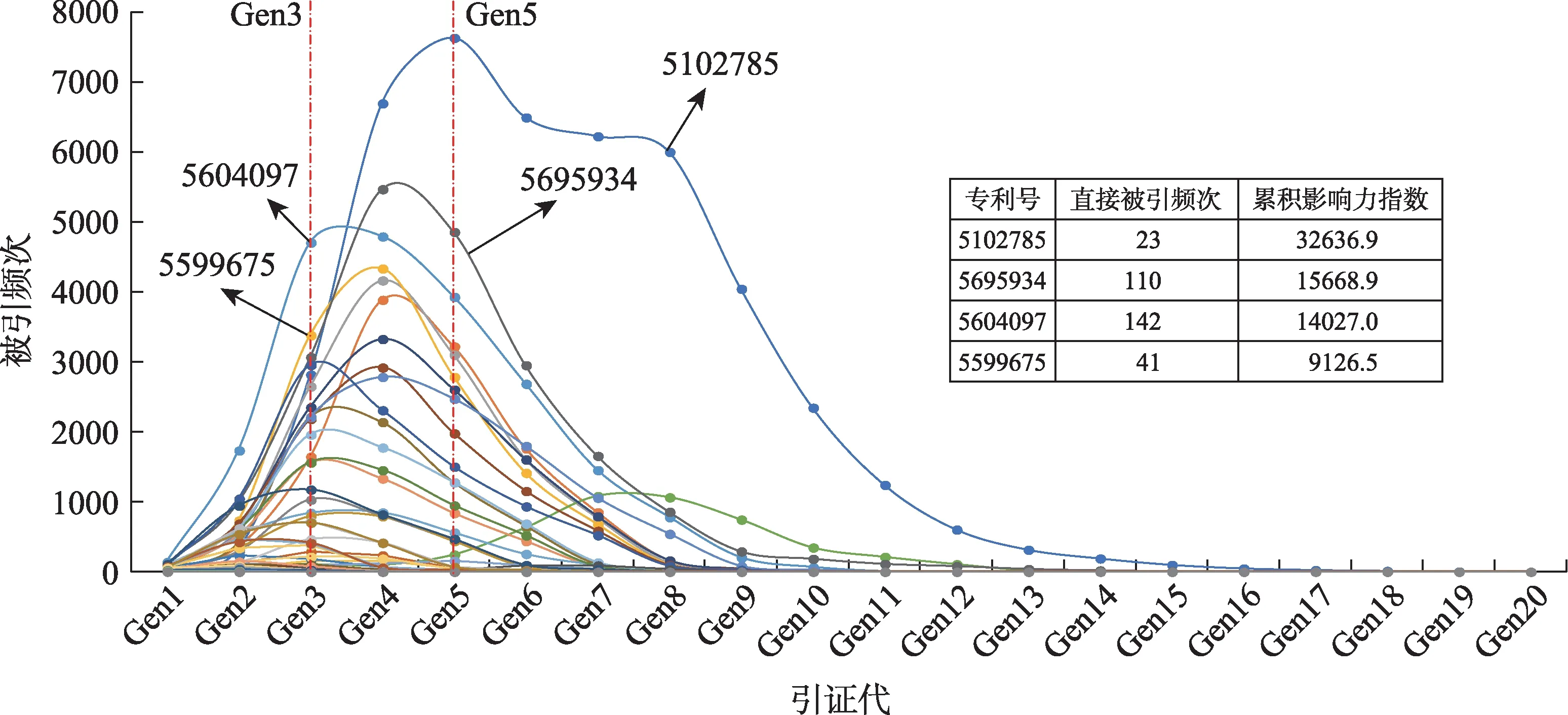
图5 各代被引频次分布情况

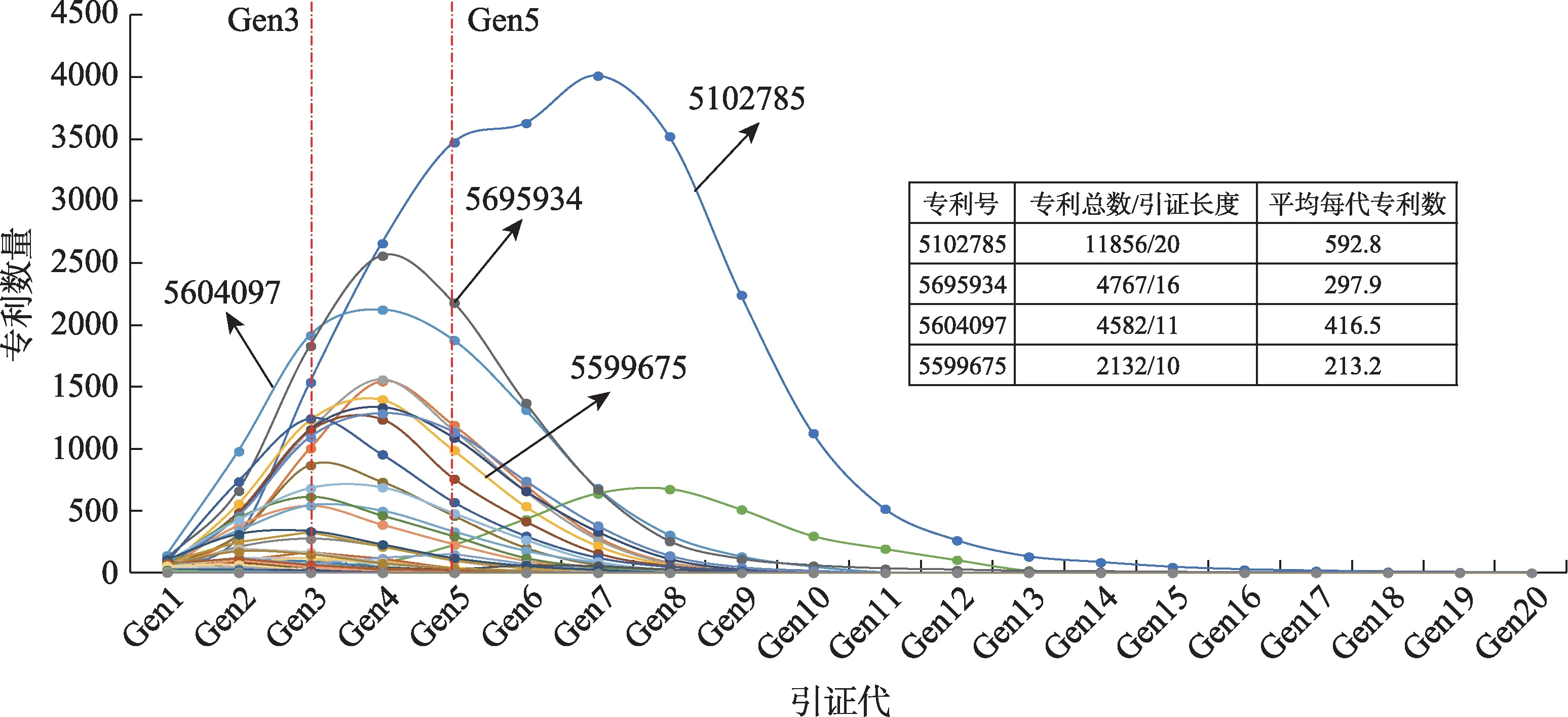
图6 各代施引专利数量分布情况

4.3 “关键节点” 的二次影响力扩散分析

事实上，专利的影响力扩散与现实中的网络传播极其相似。类比一条微博的传播过程，那么不同用户的转发就是专利之间的引用，每个用户的粉丝量就是专利的直接被引频次。已有研究证明，微博在转发过程中如果有相关机构、名人等大V 用户的二次传播，会极大的促进传播效果，引起受众的广泛关注[23]。在前文中对比分析了专利US5780231 和专利US5723598 的累积影响力差异，本文仍以二者为例，分析引证路径中的 “关键节点” 。如表5 为专利US5780231 和专利US5723598 各代高被引专利以及当代平均被引频次的详细信息，显然，专利US5780231 的引证路径中有许多被引频次远高于其本身的专利，这些 “明星” 专利在影响力传播的过程中与微博转发中的大V 用户有着相同的作用，大大提高了扩散速度和传播效果。相反地，专利US5723598 却没有这样的传播优势。

结合图7 所示的专利US5780231 的前向引文网络图，更加清晰地了解 “关键节点” 对影响力传播的巨大贡献。图7 中蓝色标签所在的节点是目标专利，红色节点为第一代施引专利，红色箭头指向的灰色节点为第二代施引专利。在第一代中既有普通专利（围绕在目标专利周围），也有高被引专利（绿色标签），如专利US7323305、US7244559 和US6620584 等高被引专利，明显可以带来更多的被引机会。不仅如此，高被引专利还可以大概率传播到其他的高被引专利，再一次促进影响力扩散。例如，第二代施引专利中的高影响力专利（暗黄色节点），其中专利US7211390 引用专利US6620584，专利US7948015 引用专利US7244559，专利US7595883引用专利US7323305，等等。由此可见， “关键节点” 专利对整体引文网络的影响是巨大的，能够很大程度上促进引文网络的传播速度和扩散范围。

表5 专利US5780231和专利US5723598的各代高被引专利

图7 专利US5780231的前向引文网络

4.4 基于被引频次和引证长度的专利分类

上文中详细研究了专利累积影响力差异的相关因素，证明了引证长度和专利总数对专利影响力的扩散起着至关重要的作用。在评价或者衡量一个专利的影响力时，尽管这两项指标有准确的区分度，但在实际的操作性方面，引证长度可以通过最长路径算法获取，而专利总数计算却比较困难。由于直接被引频次是第一代的施引专利数，数值越高代表有更大的潜在被引机会，在一定程度上对专利的累积影响力有着预测作用，且比较容易获取。因此，本文采用直接被引频次和引证长度两个指标对目标专利进行分类，分析不同类别的专利累积影响力的变化。首先，对指标进行标准化处理（均值为0，标准差为1），具体公式为其中，μ为数据均值；σ为标准差。

根据标准化后的数据得出具体的分布结果如图8 所示。图中横纵坐标中的0 值代表两指标的均值，以均值为阈值将75 个目标专利分成四种类型：长路径高被引型、长路径低被引型、短路径高被引型和短路径低被引型。根据前文所述，一般长路径高被引型专利累积影响力偏高，如专利US5604097、US5695934 等处在第一象限的专利。然而，这并不代表其他类型的专利一定差。从累积的思想来看，高被引只是在第一代中拥有优势，后续引证代的发展同样重要，如第四象限的 “黑马专利” ——US5102785，尽管其直接被引频次低，但是随着逐代影响力的累积，总影响力反而后来居上。

随着影响力的扩散和引证代的变化，不同类型的专利之间可不断地转化。新的专利产生之后，短时间内不会受到其他专利的注意，这些专利便属于短路径低被引型；一段时间后部分高质量专利开始被注意，引用次数迅速增加，进而发展为短路径高被引型；而高被引则会产生更大的被引机会，促进引证代的增加，最后这些专利便慢慢转化为长路径高被引这些高影响力专利。当然，有些普通的专利可能一直停留在第三象限，或者引证代也会慢慢增加，发展到第四象限，但累积影响力不高。

5 结论与展望

本文基于一种新的计量指标——累积影响力指数，通过对全代引证的深层次挖掘，对专利累积影响力进行研究。研究结果认为，对于专利影响力评价，累积影响力指数在保留直接被引频次优势的基础上，较好地综合了专利影响力扩散的 “广度” 和 “深度” ，能够发掘出 “隐藏” 的高影响力专利；专利的各代被引频次以及各代施引专利数近似呈 “正态分布” ，引证过程先复杂后简单；引文网络中的 “关键节点” 对目标专利影响力的传播贡献很大；直接被引频次越高代表着专利被引证的潜力越大，技术扩散速度越快；短路径高被引型专利是潜在的高影响力专利，长路径高被引专利累积影响力高，但长路径低被引专利累积影响力不一定低。

诺贝尔博物馆馆长古斯塔夫·谢尔斯特兰德曾指出， “科学家并不会在研究获得突破后，就立即获奖” 。通常诺贝尔奖评选委员会会严格地对研究成果进行验证，部分研究成果有时甚至需要经过数十年的评估，才能确定研究价值。同样地，悉尼·布伦纳的成果在直接被引频次指标上也许并不是最高的，但是其成果累积价值一定达到了 “诺奖级” 。同样，衡量一个专利的影响力也不应只看一开始的反响，后续的发展如何更加重要。就像一些基础性专利，尽管在开始的时候没有被大量引用，但是由于其技术知识的基础性和通用性，后续就会被大量的本领域甚至其他领域的专利间接引用，因此，这些专利与那些很快就能产生很大反响的高新技术专利一样都是高影响力专利，这也是单纯依靠直接被引频次所经常忽略的。

在本文选取的累积影响力指数中，每代的权重只是单纯地依靠引证路径的长度所决定，并没有考虑专利之间具体的联系。后续的研究如果能够深入考虑每个施引专利与目标专利之间的具体联系，完善到权重当中，相信一定能提高专利累积影响力指标的准确度。同时，本文没有考虑专利引文中基于技术对比的审查员引用，可能会对研究结果产生影响，后期会深入开展更加准确的区分性研究。

最后，本文基于累积价值的思想，综合考虑专利的后续全代影响，事实上也提供了一种新的价值评价思路，这对目前的高价值专利评价指标或者体系也是一种完善思路，希望能通过未来的深入研究为我国高价值专利培育给予提示和帮助。