基于方框图分析法的负反馈放大电路性能优化
2021-04-21方卫强陈博行
方卫强,马 俊,陈博行
(1.青海师范大学 计算机学院,青海 西宁 810008;2.青海师范大学 物理与电子信息工程学院,青海 西宁 810008)
0 引 言
在电学系统中,将输出信号通过某种方式,送回到输入环节,和原输入信号合并形成净输入信号,或者单独作为输入信号,进而影响输入输出性能的措施,称为反馈[1⁃2]。
反馈分为正反馈和负反馈两种。当输出信号发生某个方向的变化,称为变化根源。变化根源回送到输入端后,会再次引起输出信号变化,称为二次变化[3⁃5]。如果二次变化与变化根源具有相同的方向,则属于正反馈。如果二次变化与变化根源具有相反的方向,则属于负反馈。正反馈的作用类似于推波助澜,会加剧变化过程。负反馈的作用是稳定[6⁃7]。
负反馈放大电路在电路优化设计中应用十分广泛,因此,为解决水质监测电路设计中信号存在不稳定的状况,本文采用负反馈放大电路来稳定信号,提高采集信号和输出信号的准确性[8⁃10]。
对负反馈放大电路的分析,常见的方法有:方框图分析法、虚短虚断法、大运放法以及环路方程法。下面着重介绍方框图分析法对负反馈放大电路的影响[11⁃13],以及如何实现信号的稳定。
1 负反馈放大电路的方框图分析法
负反馈可以帮助改善放大电路性能。为清晰表述这种改善,引入方框图分析法。
1.1 方框图分析法
典型的负反馈方框图如图1 所示。
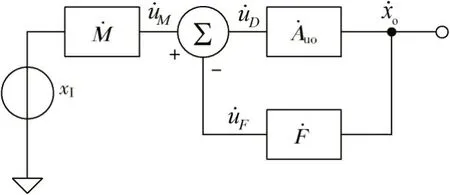
图1 典型负反馈方框图
是一 个 电压 输 入的 放 大器,其 放 大 倍 数 为倍,也称为开环放大倍数,是一个矢量表达式,含幅度增益和相移,的输出可以是电压,也可以是电流:

为反馈系数,是一个矢量,是指输出信号̇ 的多少倍,回送到了放大器的输入端。所谓的矢量,可以理解为̇表达式中包含的频率量,其幅度增益和相移是随频率变化的。多数情况下,反馈系数由纯粹的电阻分压组成,不随频率变化,比如在图2 所示的电路中,实数为。但在通用式中,还是使用̇来表达。

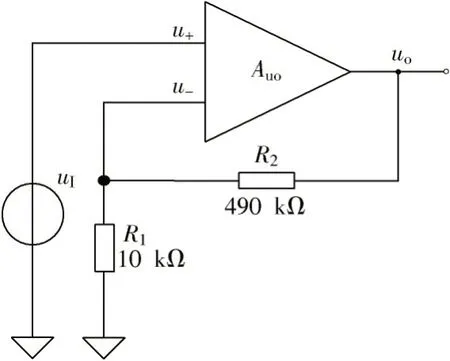
图2 典型负反馈电路
为衰减系数,是一个矢量,是指输入信号的多少倍,进入放大器的输入端。

式中xI不用矢量表达的原因是所有的相位、幅度增益都以x为基准,它是自变量,不随频率变化。
∑是一个减法器(是含相反极性的加法器),有:

据上述4 个表达式,可以列出如下方程:
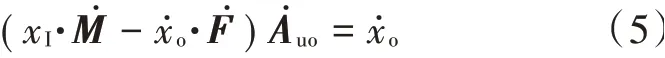
解方程可得闭环增益(是指由开环放大器组成的负反馈放大电路的增益)为:
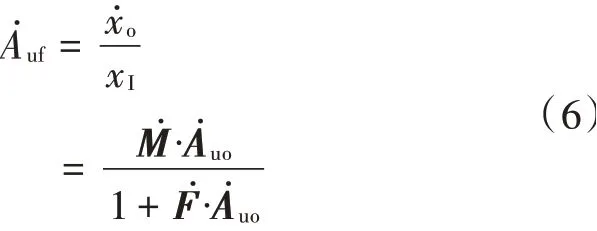

这个表达式的含义是,当开环放大器的增益和反馈系数的乘积(即环路增益)足够大(远大于1)时,也称此时为深度负反馈状态,闭环放大电路的放大倍数约为衰减系数和反馈系数的比值,而与开环放大倍数无关。
1.2 ̇和̇的求解方法
在方框图分析法中,存在两个激励:输入激励为信号源,返回激励为电路输出端。根据的定义,求解电路中的方法为:
将输出激励强制设为0,求解运放正输入端电压,用输入激励表达:

将输出激励强制设为0,求解运放负输入端电压,用输入激励表达:
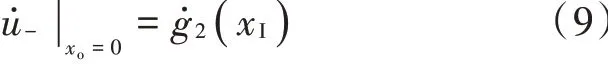
则有:
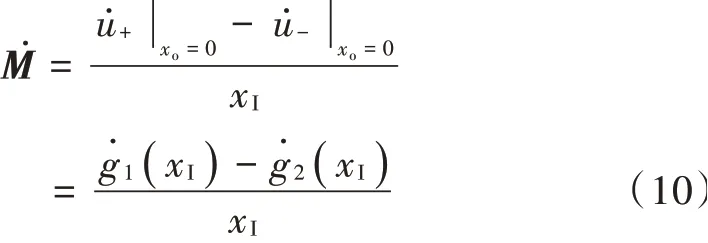
它的含义是,在不考虑输出回送的情况下,单纯的输入信号有多少加载到了运放的输入端上——运放的正输入减去负输入。
根据̇的定义,求解电路中̇的方法为:
将输入激励设为0,求解运放正输入端电压,用输出激励表达:

将输入激励设为0,求解运放负输入端电压,用输出激励表达:
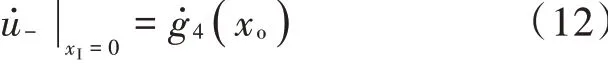
则有:
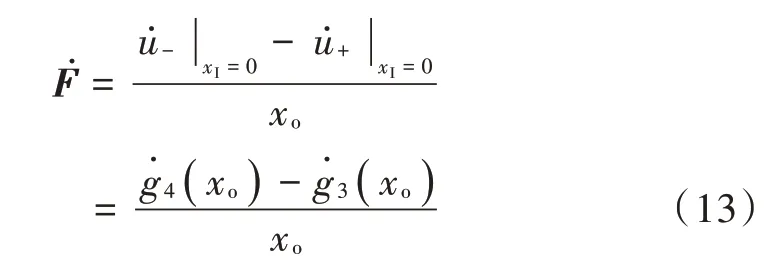
它的含义是,在不考虑输入的情况下,单纯的输出信号有多少加载到了运放的反相输入上——运放的负输入减去正输入。
对于电压输入,xI用uI表示,对于电流输入,xI用iI表示。对于电压输出,xo用uo表示,对于电流输出,xo用io表示。
利用方框图分析法,可以进行精细计算,以图3 所示电路为例。
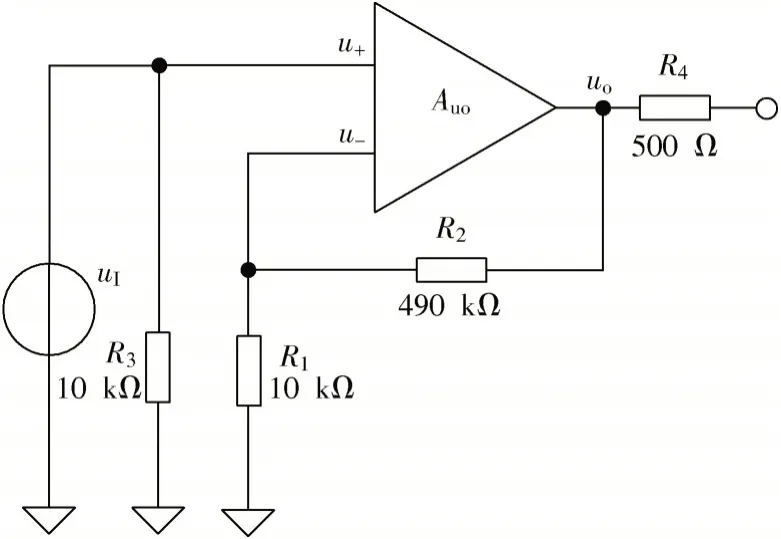
图3 改进的负反馈电路
如果已知理想运放具有确定的开环增益,且不随频率变化,那么其开环增益越大,实际的越接近50。比如,则利用式(6)得:
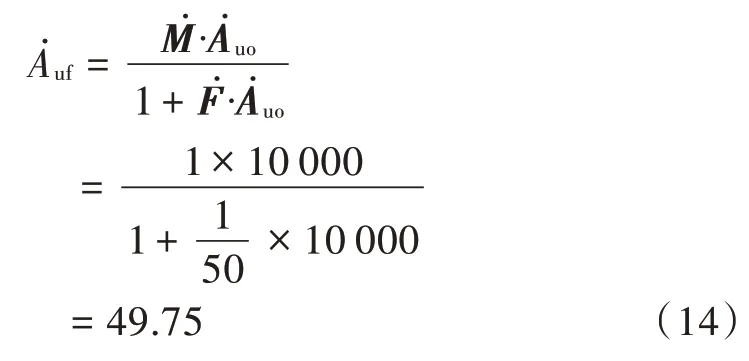
不同的,得到不同的,如表1 所示。
表1 开环放大倍数 与闭环增益 之间的关系
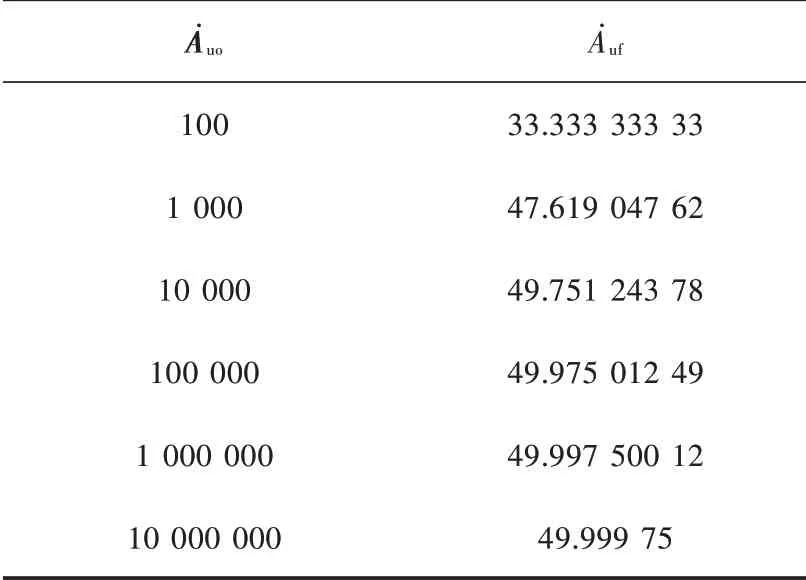
表1 开环放大倍数 与闭环增益 之间的关系
Ȧuo Ȧuf 100 1 000 10 000 100 000 1 000 000 10 000 000 33.333 333 33 47.619 047 62 49.751 243 78 49.975 012 49 49.997 500 12 49.999 75
由表1 可以看出,随着开环增益的增加,实际闭环增益逐渐逼近50。电路中,如果R1开路,R2短路,就演变成了一种特殊电路,称为跟随器。其中,̇=1,=1,闭环电压增益近似为1。
应用到水质监测电路设计中,比如pH、温度采集模块的电路设计,其电路图如图4a)所示,实物图如图4b)所示,电阻R1和R2的引入,对采集信号的稳定性有了很大提高。
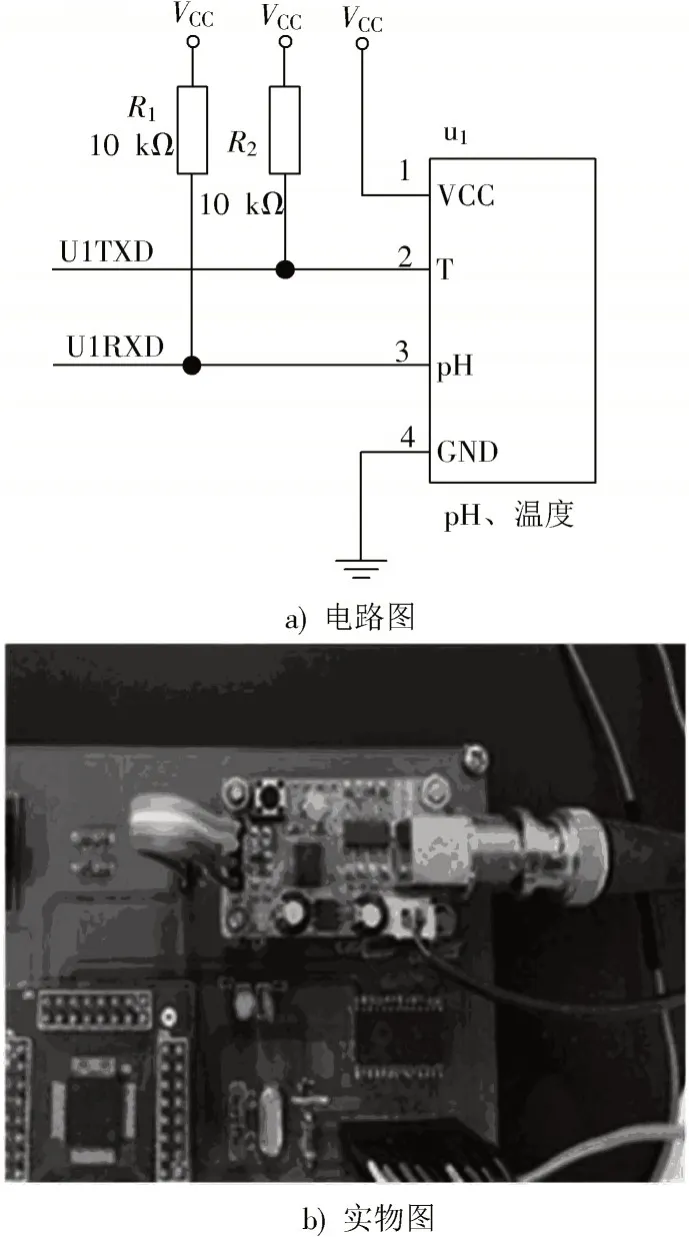
图4 pH、温度采集模块电路图与实物图
曲线图仿真结果如图5 所示,该曲线表明采集的信号抗干扰性强、稳定、准确。
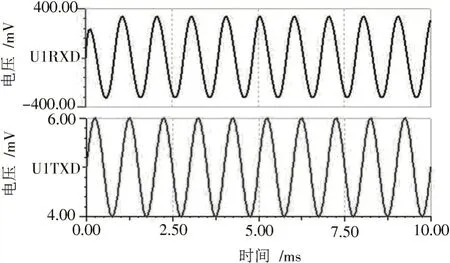
图5 信号稳态分析图
2 增益、带宽对负反馈放大电路性能的影响
开环放大器具有极高的开环电压增益,而闭环放大电路的增益会小得多,这是负反馈引入带来的“弊端”,但负反馈的引入,对放大电路的其他性能影响巨大,比如提高了增益稳定性、拓展了放大器带宽等。
利用方框图分析法,可以分析负反馈对放大电路的性能影响。
2.1 对增益稳定性的影响
由表1 中可以看出,当开环放大器的开环增益发生一定数量的改变,比如从10 000 变到100 000,含负反馈的闭环放大器之闭环增益只会出现很小的变化,从49.751 变到了49.975。这就是负反馈对增益稳定性的影响,即负反馈大幅度提高了增益稳定性。一般用增益变化量除以增益,即增益的相对变化量来表示增益的稳定性。为方便进行数值分析,将式(6)中的矢量用标量代替:
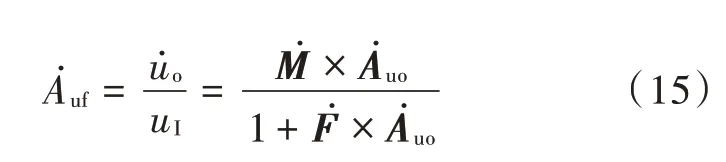

对两边同时取微分,得:
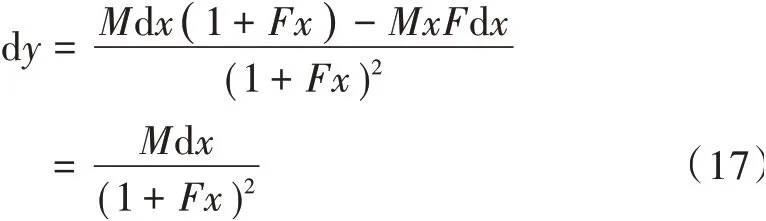
两边同时除以y,得:
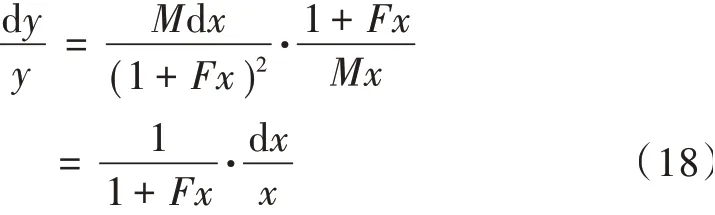
即:
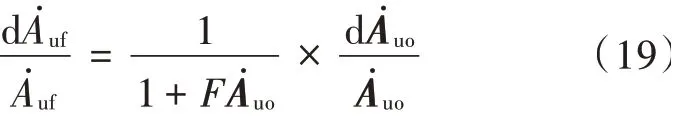
2.2 大幅度提高上限截止频率
假设开环放大器具有一阶上限截止频率fH,参照低通高通频率不同的影响,得开环增益随频率变化的表达式为:
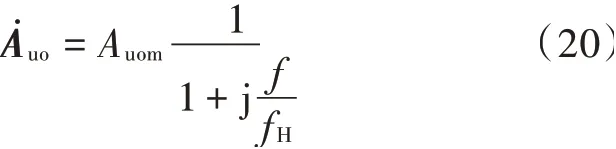
这是标准一阶低通滤波器表达式,含义是:当趋于0时,开环增益为Auom,称为中频开环增益,当f=fH时,开环增益的模,变为Auom的0.707倍,且具有-45°的相移。
将式(20)代入式(6)中,得:

式中:为中频段闭环电压增益(注意此处的中频段,在低通滤波器中就是频率等于0);后一项表达式是一个标准低通表达式,含义是闭环上限截止频率是开环上限截止频率的倍。
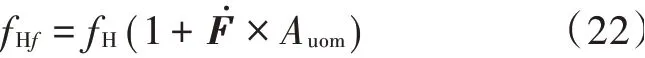
这说明,引入负反馈后,闭环电路的上限截止频率得到了很大的提高。
2.3 大幅度降低下限截止频率
假设开环放大器具有一阶下限截止频率fL,参照低通高通频率不同的影响,得开环增益随频率f变化的表达式为:
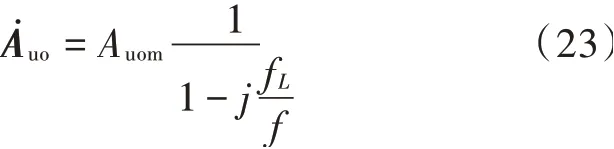
将式(23)代入式(6)中,得:
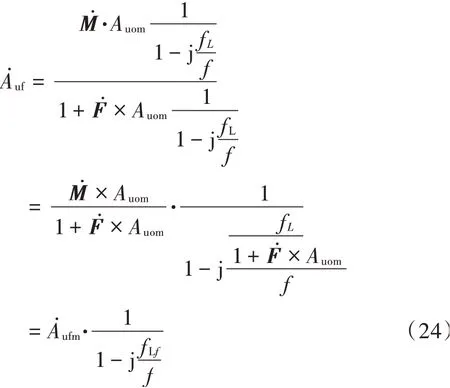

这说明,引入负反馈后,闭环电路的下限截止频率变得更低,得到了很大的拓展。
3 仿真与结果
对上限截止频率进行计算得出的曲线图如图6 所示,实曲线代表频率,粗虚曲线代表开环增益的模,细虚曲线代表闭环曲线的模。其中,频率和开环增益的模共用左边坐标的值,闭环增益的模用右边坐标的值。由图6 曲线可以看出,开环增益的上限截止频率很小,而闭环增益的上限截止频率得到了很大拓展。因此,方框图分析法的引入大幅度提高了上限截止频率,提高了负反馈对放大电路的性能。

图6 上限截止频率曲线图
利用Matlab 对下限截止频率的仿真,得到如图7 所示的曲线。
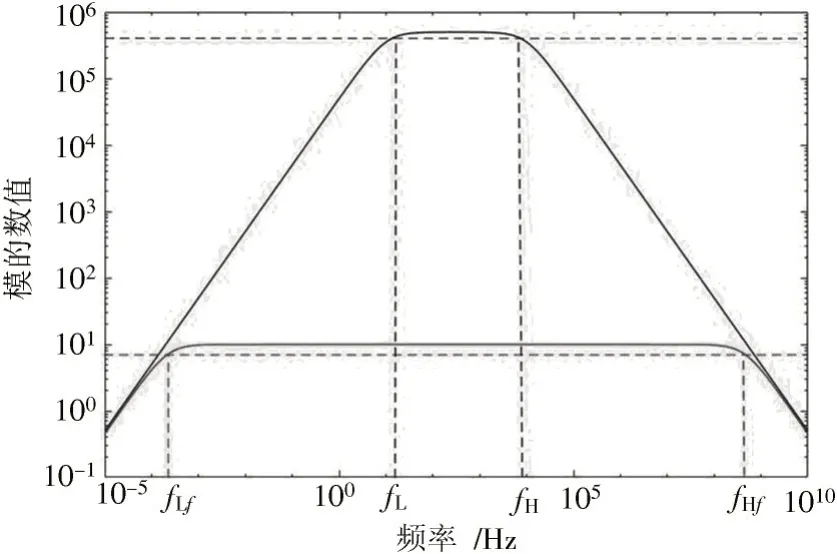
图7 下限截止频率曲线图
图7 中深实曲线为开环增益的模随频率变化的曲线,可看出其下限截止频率为10 Hz,上限截止频率为10 kHz;浅实曲线为闭环增益的模随频率变化的曲线。可看出其下限截止频率很低,而上限截止频率变得很高。该图像表明方框图分析法明显地降低了下限截止频率,从而提高了负反馈对放大电路的性能。
4 结 语
本文利用方框图分析法对负反馈放大电路进行分析优化,从而反映负反馈对放大电路性能的影响。实验结果表明,负反馈的引入明显提高了增益稳定性,闭环电路的上限截止频率得到了很大的提高,大幅度降低了下限截止频率,对电路性能有了质的提升。
