显式模型预测控制的在线迭代学习策略研究

陈 宇，刘 雪，陈 晶

（华中科技大学 电气与电子工程学院，湖北 武汉 430074）

0 引 言

模型预测控制（MPC）是在已知系统模型的基础上求解一个最优控制，根据计算方法的不同可划分为在线MPC 和显式MPC。在线MPC 是在控制过程中进行最优控制变量的求解，但由于计算量大，不适用于控制周期极短的电力电子变换器。与在线MPC 相比，显式MPC首先离线计算出优化控制规律的集合，再将该集合存储于控制器中，供在线查询与计算使用，因而有效减少了在线求解时间[1]。

显式MPC 的控制律集合是由大量参数表述的。实时控制时，首先需要根据实时状态反馈查找合适的控制规律，再计算出控制参数，查找和计算时间仍然较长。为此，通常事先将连续的状态空间进行离散，将离散值代入相应的控制律中，计算得到对应的控制变量，从而构成以状态空间为输入、控制变量为输出的表格。将该表格存储在控制器中，就可根据反馈状态直接查询得到控制变量[2⁃3]。

显式MPC 在负载投切等工作点小范围变化工况下控制性能较好，但在启动过程等工作点大范围变化工况下控制性能不佳。为解决这一问题，本文设计了一种在启动过程中对表格进行迭代修改的方法。该方法借鉴了迭代学习的思想[4⁃9]，即首先让电力电子变换器在已有控制规律下运行一轮，将运行一轮过后的波形与期望波形进行比较，对控制规律进行若干修正。这一过程不断迭代进行，使实际波形与期望波形的误差不断减小。

本文以Buck 变换器[10⁃11]为例展示显式MPC 的在线迭代学习策略。该策略在Buck 变换器启动过程中不断对控制表进行修改，在不降低负载投切控制性能的同时，有效提升了启动过程的控制性能。仿真结果亦证明了所提方法的有效性。

1 MPC 的工作原理简述

1.1 Buck 变换器简述

Buck 变换器如图1 所示，其中，S，D 分别为开关管和续流二极管；L，C和Ro分别为电感、电容和负载电阻。当开关管S 导通时，电感电流iL线性上升，电能经电感L供给电容C与负载电阻Ro，同时电感L储存能量；当开关管S 关断时，电感电流iL经D 续流构成回路，iL线性下降，电感L中储存的磁能转化为电能继续供给电容C与负载电阻Ro。为便于下文论述与讨论，Buck 变换器的参数如表1 所示。

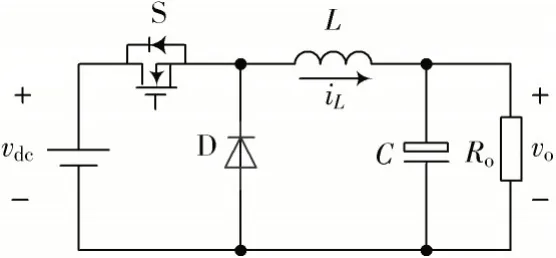
图1 Buck 变换器

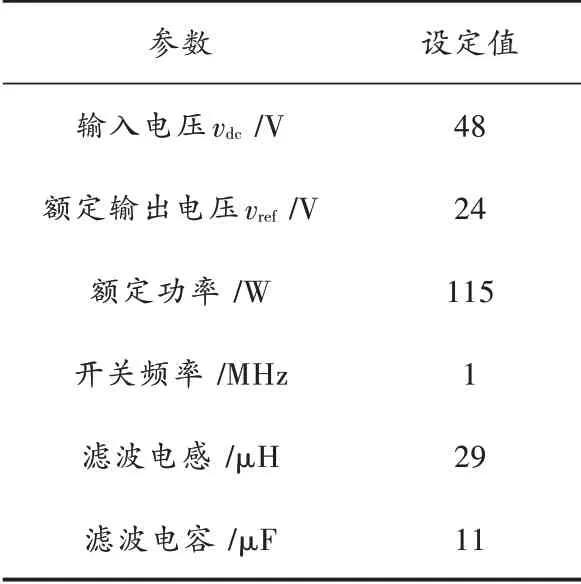
表1 Buck 变换器参数

1.2 显式MPC 简述

为展开显式MPC 设计，需首先得到Buck 变换器的状态空间平均模型：

式中vo为输出电压。

本文中显式MPC 的控制目标是将vo在LPH步内调节到参考电压vref，首先定义目标函数：

式中：LPH为预测的步长，文中设定LPH=20，即希望vo可在20 步以内达到给定值；vo（k+l|k）表示第k步采样值下，基于一组输入量所计算的第k+l个状态量，在本文的设计中，通过试探法将加权系数[12]设置为q=100。

此外，显式MPC 还允许定义状态变量vo和iL，以及控制参数dBuck的相关约束，使其不超过其物理限制，例如令：

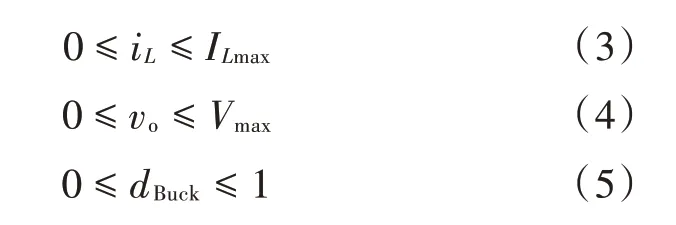
式中：ILmax为使电感磁芯饱和的电流值。本文中设为ILmax=10 A；Vmax的设置是为了避免输出电压超调，本文中设为Vmax=30 V。

为使成本函数J的值最小，借助多参数线性规划工具箱（MPT）[13]，可方便地离线生成所需的控制律，在此不详细展开叙述。控制律会将状态空间分割成图2 所示的大量区域，当状态变量vo和iL落入该区域时，根据对应区域的增益矩阵与偏置矩阵计算得到dBuck。

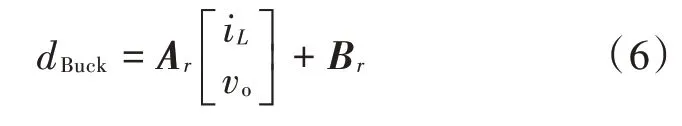
式中：Ar和Br为第r个区域的增益矩阵和偏置矩阵，由MPT 生成。

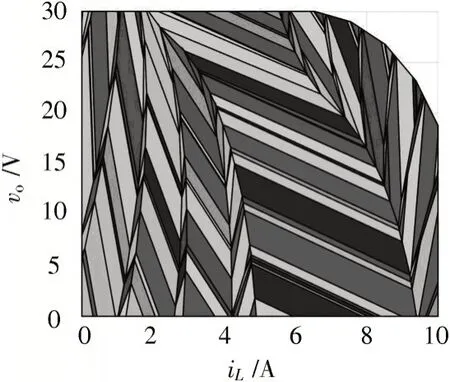
图2 MPC 控制律的区域划分

按式（6）进行计算需要大量检索与计算时间。为简化计算，在实际应用时通常将vo和iL均匀划分成N等份（在本文中取N=60），则整个求解区域被划分成N×N的区间，取每个区间中点的vo和iL代入式（6）计算出相应的dBuck，从而将求解区域离散成一张60×60 的控制表，当状态变量vo和iL落入某区间时，即用该dBuck实施控制。存储该表需要3 600 个存储单元，但免去了查找区域，取出增益矩阵、偏置矩阵以及进行计算的时间，实时性得到极大提升。为便于下文进一步讨论，以vo为x轴，iL为y轴，dBuck为z轴，将离散后的表格绘制成如图3 所示的三维图，由图3 可直观地看出，在不同的（vo，iL）组合下，查找得到的dBuck均不相同，且由dBuck组成的曲面基本光滑，保证了调节过程的连续性。

依上述设计，可得图4 虚线框所示的MPC 系统。在每一个开关周期内，控制系统均对vo和iL进行采样，经AD 转换单元送入控制器，在控制器里依图3 控制表的x轴与y轴进行定位，取出对应z轴的占空比dBuck，经PWM 单元产生开关管S 的驱动信号，形成闭环反馈。

图3 离散化的控制表

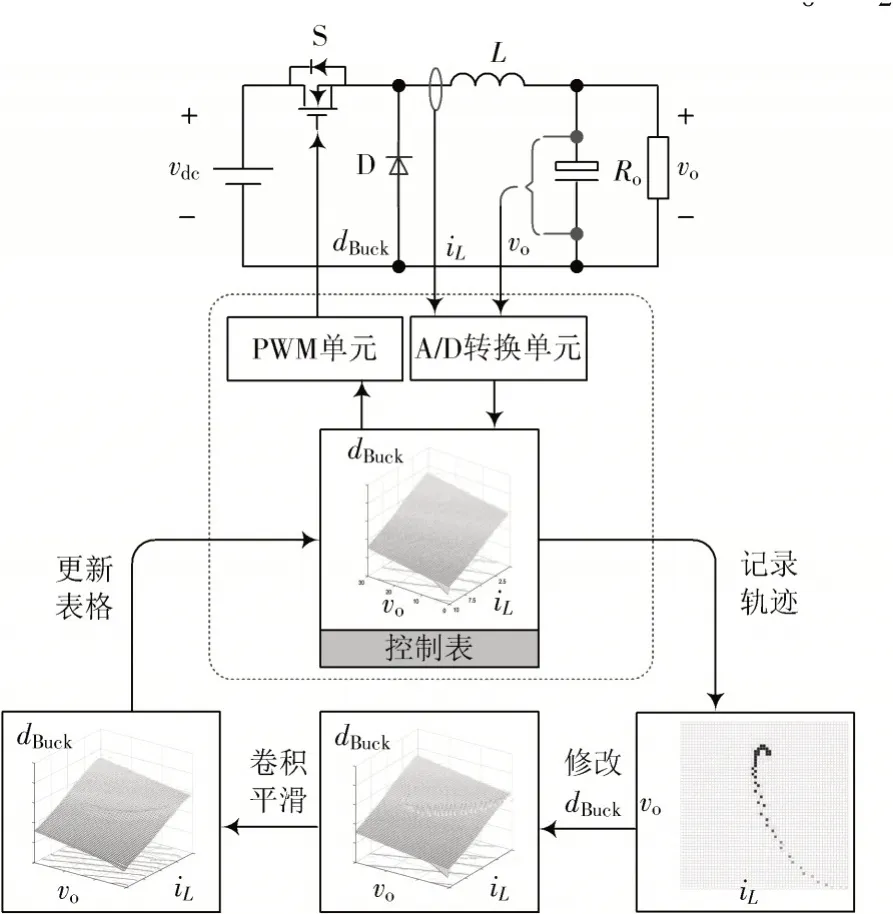
图4 Buck 变换器控制示意图

2 在线迭代学习策略

本文提出的在线迭代学习策略可在已有显式MPC控制系统中增加，如图4 所示。首先，在Buck 变换器启动过程中记录vo和iL的运动轨迹；其次，以vo轨迹逼近期望轨迹vref为目标，将启动过程所经过的运动轨迹对应的占空比dBuck进行修改；最后，将修改过的控制表用卷积运算进行平滑处理，并将平滑处理后的控制表用于下一轮迭代。下面将对上述过程进行详细论述。

2.1 启动过程运动轨迹记录

图5 给出了Buck 变换器在MPC 下的启动波形。其中，图5a）为vo随时间变化的波形，由图可见启动过程较慢，且有超调；图5b）为iL随时间变化的波形；图5c）为vo和iL的运行轨迹，即图3 控制表中的x⁃y平面。在Buck变换器启动前，vo和iL均为0，处于图中的A点，依该状态查表，可得到对应的占空比dBuck，该占空比作用于Buck变换器上，使vo和iL产生变化，如此循环直到Buck 变换器的输出电压vo达到vref。本设计中，从A点到B点，共计记录M=90 个点的运行轨迹。

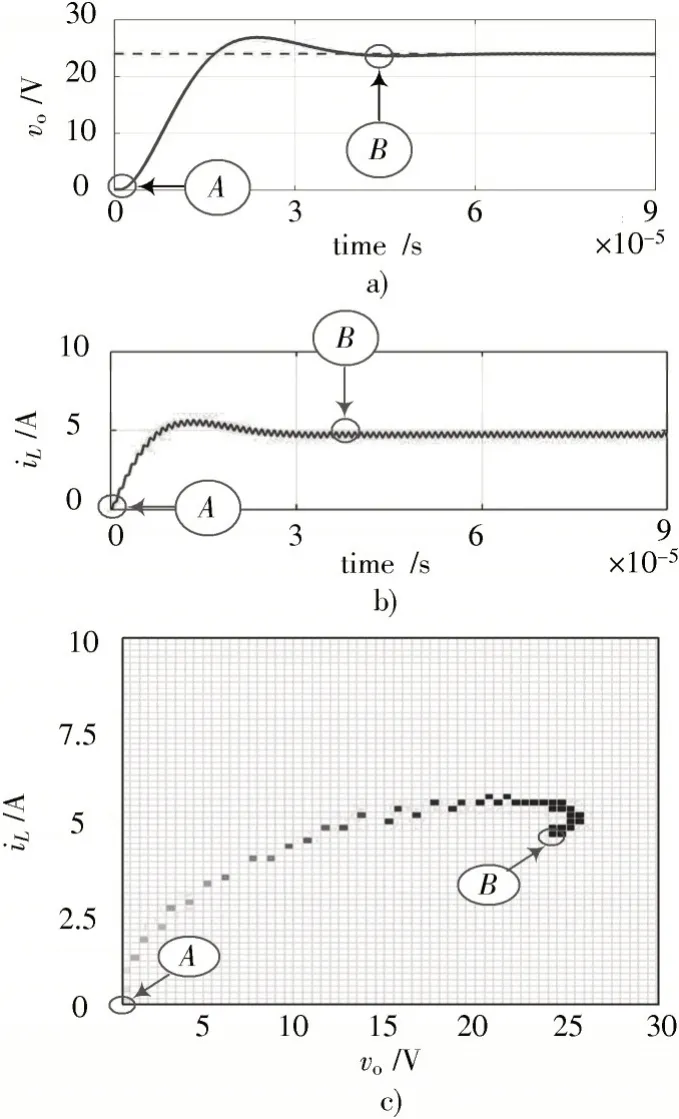
图5 Buck 变换器的运行轨迹

2.2 控制表的修改

定义一个迭代周期内输出误差的总和E：

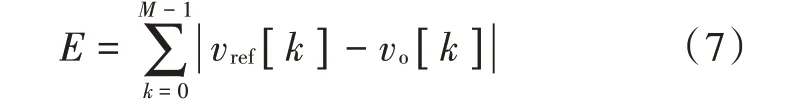
式中：vref[k]和vo[k]为第k个开关周期的期望电压和输出电压；以E为基础修改运行轨迹对应的占空比dBuck，修改原则是使E尽可能小。首先定义惩罚函数Q[k]：

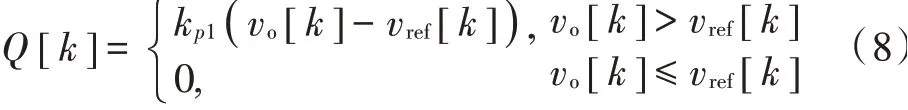
式（8）的意义是：若当前vo[k]出现超调，即高于vref[k]时，Q[k]给出一定惩罚量，强度由超调量和kp1调整系数给出；否则Q[k]=0。基于Q[k]设计占空比dBuck的修改法则：

由于电路具有迟滞性，所以k拍的输出，是由k-1 拍的占空比决定的。式（9）右边第一项dBuck[k-1]为上一拍（即iL[k-1]，vo[k-1]）对应的占空比。第二项加上E乘以调整系数kp2和（M-k）后，对经过轨迹上的占空比进行调整，以加快动态响应。（M-k）的作用是在启动初始阶段k较小时使dBuck增加的幅度较大，从而使vo上升的速度较快，而随着k增大，使dBuck的增加幅度变小，以便vo可更快趋于稳定。第三项为惩罚函数，可在超调出现前及时减小占空比，抑制超调的出现。按式（9）修改一轮后的控制表如图6 所示。在曲面上突起的点，即为运行轨迹被修改过的dBuck值[14]。

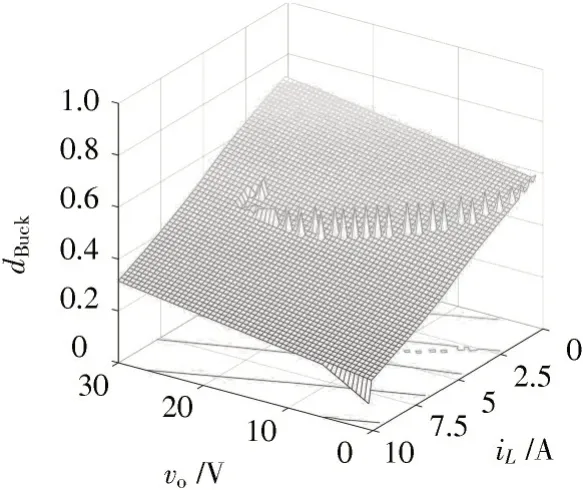
图6 修改运行轨迹后的控制表

2.3 控制表的卷积

图6 中可见，本轮迭代修改了此次运行轨迹上的占空比。在下一次启动过程中，由于第k-1 拍占空比已修改，将造成k拍运行轨迹的改变。因此，新运行轨迹与原运行轨迹必将有所偏差。为将本次迭代学习的效果扩大到控制表中本次运行轨迹附近的位置，以对下次运行起作用，需对控制表进行平滑处理，为此对控制表进行二维卷积。卷积定义为：

式中：A为卷积核；B为被卷积的二维变量（即控制表）；p和q会遍历所有可得到的A(p,q)和B(j-p+1,i-q+1)合法下标的值。现以式（11）为例展示卷积的效果。设卷积核A中的所有元素均为，B中仅有对角线元素为1，其他元素为0。将A和B的卷积结果与B相比可见，卷积结果的对角线附近的数值都有所增大，即对二维变量进行了空间上的平滑处理[15]。

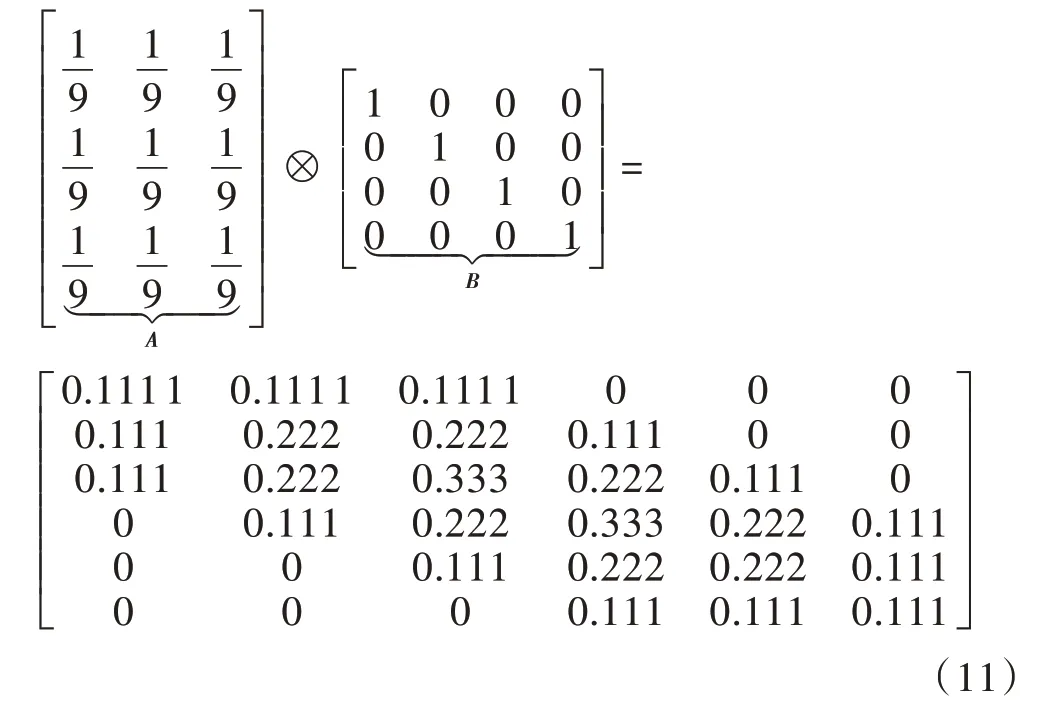
在本文的设计中，A为一个5×5 的二维变量，元素的总加权系数为1，B为上述修改过的控制表。用A对该控制表做卷积后，所得的控制表如图7 所示，可见控制表已经得到了平滑处理。

图7 经卷积运算后的控制表

2.4 下一轮迭代学习

在完成本次迭代后，将更新后的控制表重新用于Buck 变换器的控制中，得到下次启动过程的运行轨迹，如图8 所示。由图8a）可见：vo的启动过程较上一轮更快，超调量也更小；由图8b）可知，对应的iL也与上一轮所有不同；由图8c）可见：启动过程的运行轨迹亦与上一轮有所不同。由于对控制表进行了卷积平滑，新的运行轨迹上的对应占空比亦已被修改，因此可保证连续平稳的运行。

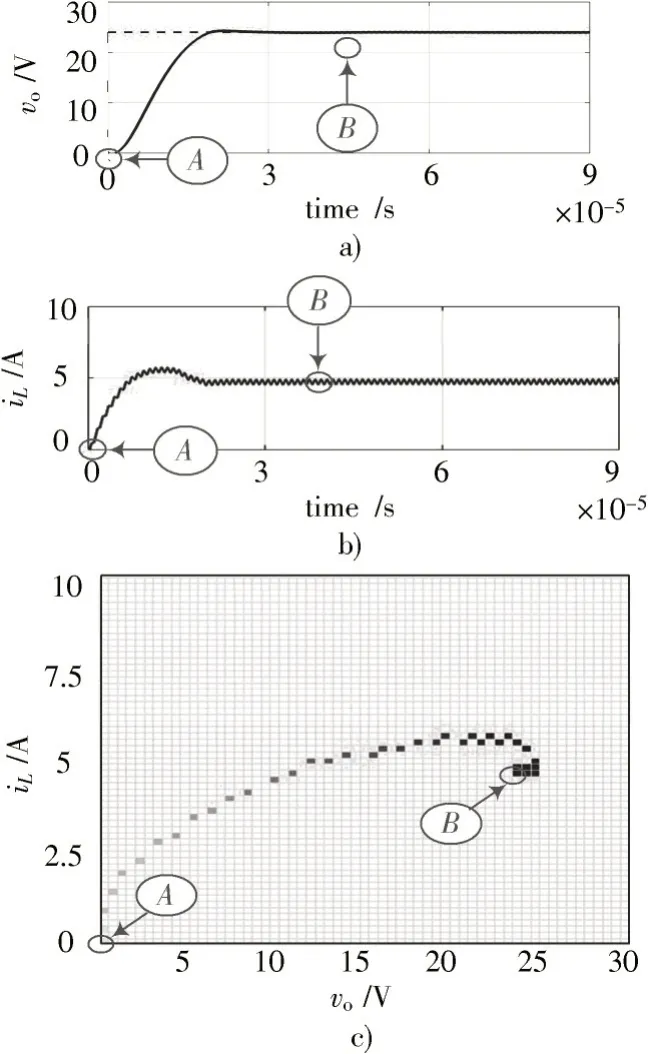
图8 迭代后的运行轨迹

3 仿真验证

3.1 仿真参数设定

本文通过Matlab 软件仿真，对基于迭代学习的Buck 变换器进行了仿真验证。仿真参数与表1 一致。

3.2 仿真结果分析

在迭代开始时，首先将控制表应用于Buck 变换器的控制中，得到迭代学习的过程如图9 所示，起始时间为0，输出电压vo从0 开始启动并稳定在24 V，然后将dBuck置0，模拟电力电子变换器停机，后续电压从24 V 下跌并稳定至0。在启动过程中对控制表进行修改并不断迭代，从而得到图9 中电压不断上升和下跌的波形。

由图9 可看出，在第1 个迭代周期内，vo超调较大，此时由于惩罚函数Q[k]的作用，在第2 个迭代周期超调已经有所减小，至第5 个迭代周期超调已基本消失，在控制表的三维图像里表现为曲面内有一处凹陷。同时，kp2（M-k）E项使经过轨迹上的dBuck增大，在图9 中表现为曲面内运行轨迹经过的地方凸起，其中，第11 个迭代周期的凸起程度较第2，5，8 个迭代周期都有所增加。由于（M-k）的作用，轨迹起始阶段凸起较高，后续凸起较低。

若迭代学习过程中超调再次出现，则Q[k]将重新发挥作用将其消除。最终E值达到动态平衡，迭代结束。

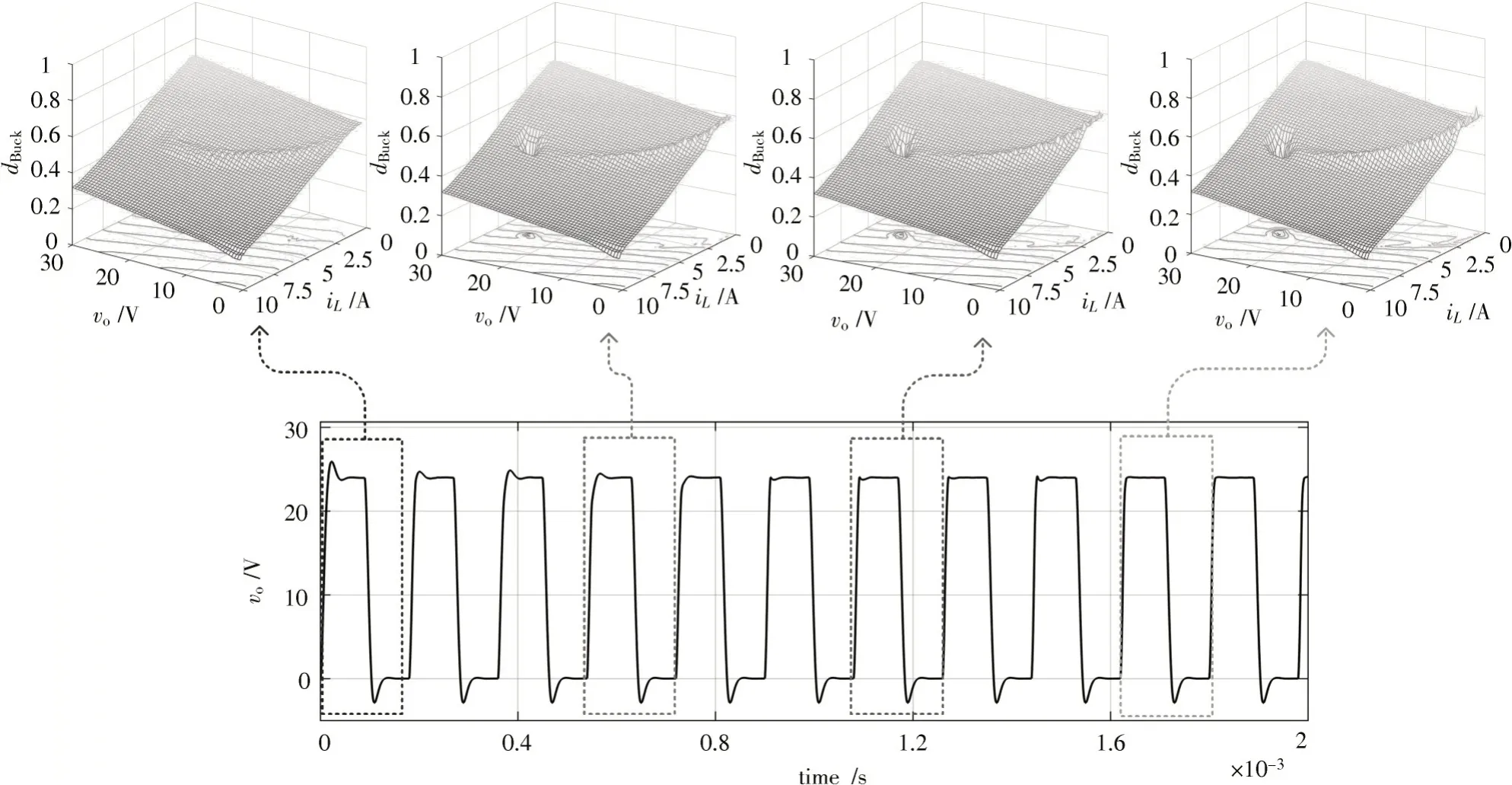
图9 迭代学习的过程

迭代学习完成后的启动控制性能如图10 所示，相比于未修改前的响应曲线，输出电压的暂态响应明显增加且基本上无超调。图11 给出Buck 变换器稳定运行后从半载突加满载的波形，可见采用文中所提出的迭代学习方法并不会对负载投切的控制性能造成影响。

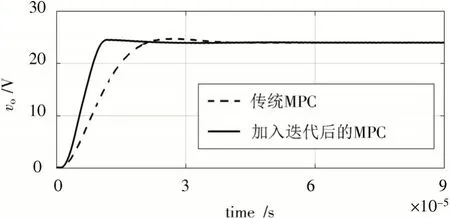
图10 迭代前后启动过程的vo曲线

4 结 论

本文提出一种显式MPC 控制表的迭代学习方法，以提高启动过程的控制性能。以Buck 变换器为例，首先对Buck 变换器进行数学建模，生成相应控制表，再给出启动过程中控制表的修改方法，最后通过仿真验证了方法的准确性。从仿真中可见，在迭代学习的过程中，Buck 变换器启动过程的动态响应不断加快，同时超调也得到了有效抑制，并且该方法可推广于各类采用了显式MPC 的电力电子变换器中。

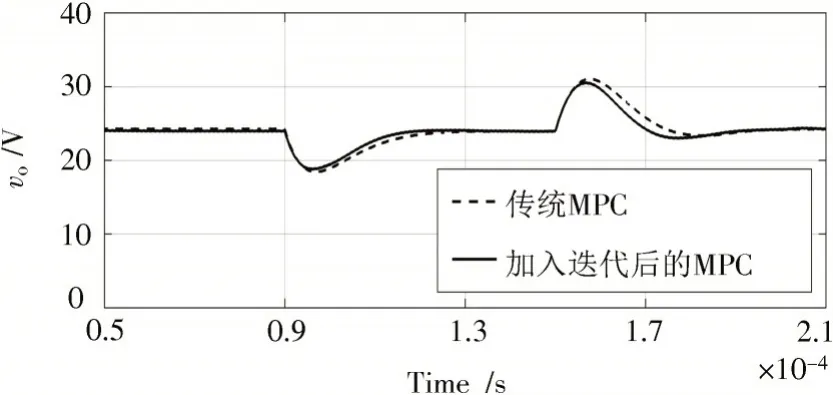
图11 迭代前后负载投切的vo曲线