变步长搜索的计算全息图编码方法
2021-04-20邱宏伟金春水张海涛王丽萍孙诗壮
邱宏伟,金春水 ,于 杰,刘 钰,张海涛,2,王丽萍,孙诗壮
(1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100039)
1 引言
计算全息图(CGH)作为非球面零位补偿检测的关键器件,被广泛应用于非球面检测[1-4]。与传统的Dall[5]和Offner[6]补偿器不同,CGH 是一种衍射光学元件,它利用光的衍射效应生成与被检非球面面形匹配良好的非球面波前,从而实现非球面的零位检测。高精度CGH 编码是实现高精度非球面检测的关键之一。
计算全息编码是指将CGH 相位转换为刻蚀设备可识别的量化位置数据[7]。由于刻蚀设备只能以折线的方式进行刻蚀,因此需将光滑条纹离散成多边形。为了保证编码精度,通常采用高密度采样逼近理想曲线,从而实现高精度编码。然而,高密度采样意味着编码数据量巨大,导致刻蚀设备内存负担加大,大大增加了刻蚀时间[8]。因此,需要选择合适的方法对CGH 进行编码。
目前,常用的CGH 编码方法有迂回相位编码法、修正离轴参考光编码法、相位轮廓测量术及计算全息干涉编码法等[9]。其中,迂回相位编码法需近似取值,因此总会引入相位误差,且迂回相位编码方法实现非常困难,不利于产生非球面波。修正离轴参考光编码法由于需要与参考光进行叠加运算,因此增加了计算量。另外,这些方法要实现高精度编码都会使得编码数据量巨大。
针对迂回相位编码不利于产生非球面波的缺点,Jiao Fan 等提出逐点追迹法进行计算。虽然该方法能很好地控制误差,但求解过程太过复杂[10]。
为了克服上述问题,Ma Jun 等人提出了一种在不同径向位置选择不同采样密度的方法来近似计算全息图条纹,但是该方法对于曲率连续变化的条纹近似效果并不理想[11]。
针对迂回相位编码、修正离轴参考光以及计算全息干涉等编码方法存在的编码精度与编码数据量之间的矛盾,本文提出了一种变步长CGH编码方法。该方法根据编码精度的需求可以简单便捷地选择采样步长,以最小的编码数据量实现高精度编码。该编码方法还具有能够减轻刻蚀设备内存负担以及降低CGH 制作时间成本等优点。
2 编码原理
假设CGH 产生的波前相位函数表示为Φ(x,y),并令:
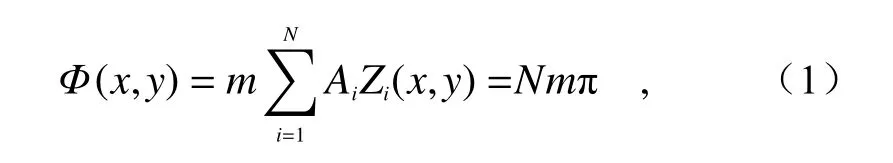
其中N为整数,m为衍射级次。函数Φ(x,y)的编码过程如图1 所示。由图1 可知,CGH 的编码过程可分为两步:首先,解算式(1)得到等相位曲线分布,如图1(a)所示;然后,将得到的各等相位曲线离散采样,实现量化编码,如图1(b)所示。

图1 CGH 编码过程。(a)由相位轮廓干涉图计算相位函数;(b)条纹编码成多边形Fig.1 CGH encoding process.(a)Wavefront phase function calculated by phase contour interferograms;(b)encoding the fringes into polygons
传统的CGH 编码方法采用增大采样密度的方式来提高编码精度。然而,这一方式虽可提高精度,但相应的编码数据量将急剧增加。为了减少编码数据量,同时最大程度地提高编码精度,本文提出基于相位分布梯度大小选择采样密度的方式来实现目标。编码过程如下:
(1)根据被测非球面设计CGH,并计算相位分布Φ(x,y);
(2)计算Φ(x,y)的梯度分布;
(3)根据Φ(x,y)的梯度分布情况动态选择采样步长进行编码,并保存数据;
(4)将数据转换为GDS II 或OASIS 等刻蚀机器可读格式。
CGH 的相位函数表示为Φ(x,y),那么其在二维矢量场的梯度为:
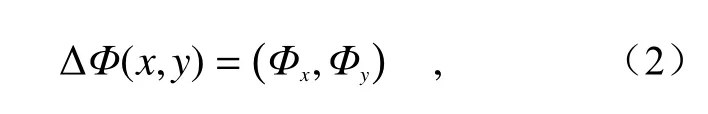
其中Φx=[∂Φ(x,y)/∂x],Φy=[∂Φ(x,y)/∂y]。
等相位曲线离散采样过程如图2 所示,在这一过程中,会不可避免地导致实际条纹与理想条纹产生偏差,根据前人的分析,编码误差与波长、衍射级次及编码偏差成正比,与局部条纹周期成反比[12]。因此,引起的局部波前误差∆WRMS(x,y)可表示为:
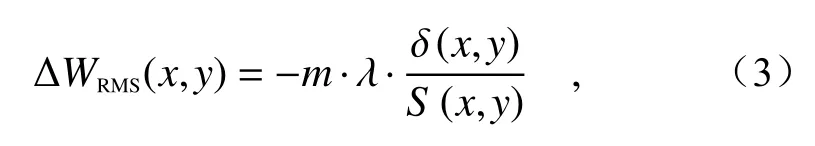
其中,λ为波长,S(x,y)为局部条纹周期,δ(x,y)为实际条纹与理想条纹的偏差。
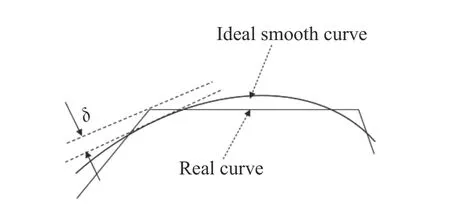
图2 理想条纹数值化示意图Fig.2 The digitization process of ideal fringe
为达到满足使用需求的编码精度,需要减小编码的局部偏差δ(x,y)。局部偏差δ(x,y)与编码采样步长L(x,y)的几何关系如图3 所示。
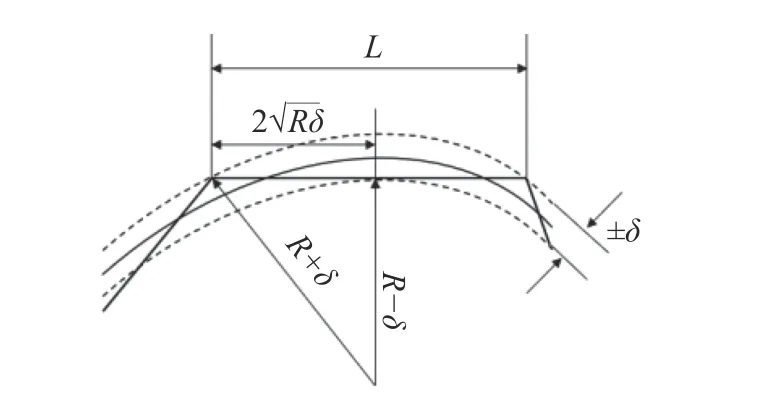
图3 编码采样步长与编码偏差几何关系图Fig.3 Geometric relationship between encoding sampling step and encoding deviation
由图3 可知两者满足以下关系
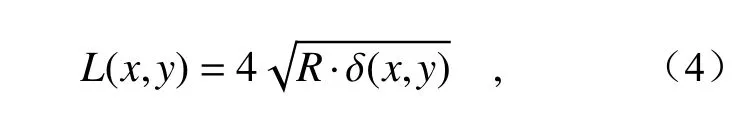
其中R=1/c,σ=δ(x,y)/S(x,y)。
根据采样频率与采样步长的关系,采样频率γ(x,y)可表示为:
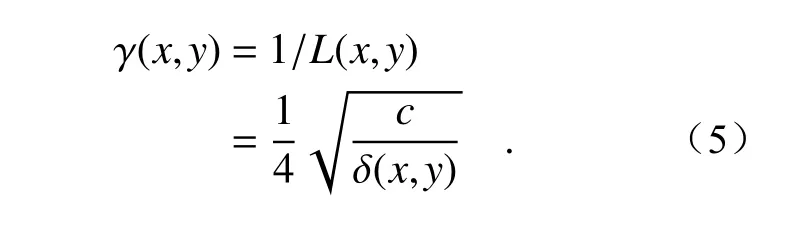
其中,c=1/R。根据Wenrui Cai 的分析,采样频率γ(x,y)可表示为[11]:

通过上述分析,建立了采样步长与编码误差之间的联系。为动态选择编码步长,需先确定编码所需达到的精度。根据式(7)可得:

至此,便可根据编码需求动态选择编码步长进行编码。由于刻蚀机器只能识别特定格式的文件,因此需将编码数据转为GDSⅡ格式文件[13-14]。
3 仿真过程
对一高次非球面设计了零位补偿CGH,非球面可表示为:
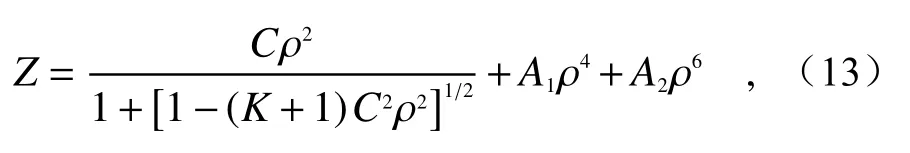
式中Z为非球面矢高,K为二次曲面常数,A1、A2为高次项系数,ρ为非球面径向坐标,C为非球面顶点曲率。非球面的具体参数如表1 所示。

表1 非球面参数Tab.1 Parameters of the aspheric lens
在计算全息图的设计阶段,必须考虑以下4 个方面:衍射杂光的分离与去除、降低条纹密度、限制CGH 口径以及约束投影畸变。为提高CGH的设计效率,建立了CGH 设计模型[5]。该模型综合考虑了上述4 方面,将非球面参数代入模型,得出CGH 在光路中的位置与所需加载的载频量(其中CGH 口径为63 mm),利用等光程原理计算CGH 相位,相位分布如图4(彩图见期刊电子版)所示。对相位梯度进行求解,结果如图5(彩图见期刊电子版)所示。

图4 CGH 相位分布示意图Fig.4 Phase distribution of the CGH

图5 CGH 相位函数梯度分布Fig.5 Gradient distribution of the CGH phase function
根据第2 节所述的编码原理以及编码精度要求,将编码误差容限设为0.03 nm,编写程序对CGH进行编码,结果如图6(彩图见期刊电子版)所示。编码后的最小条纹间距为11μm,最大条纹间距为480μm。完成上述过程后,利用传统编程方法对同一CGH 进行编码,其数据量高达160 GB,本文所提出的方法数据量仅为3 GB,且相较于传统方法,其计算时间大大缩短,仅为16 小时。
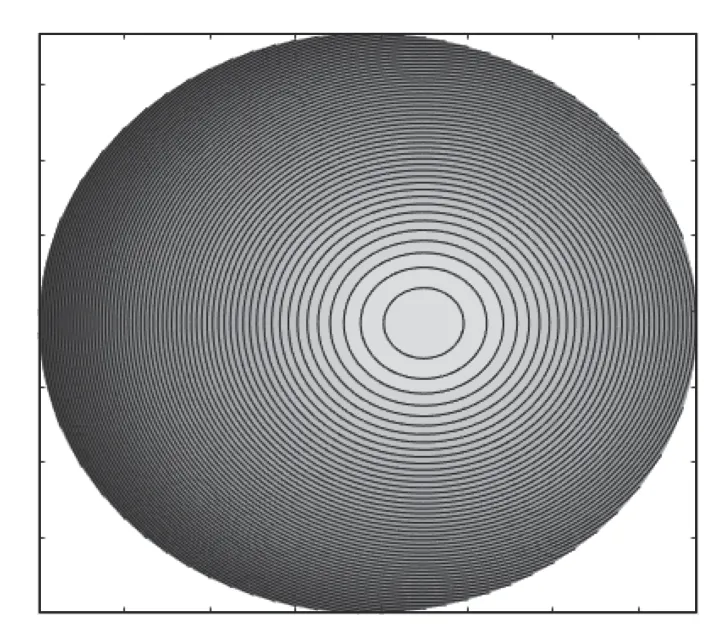
图6 CGH 条纹分布示意图Fig.6 Fringe distribution of CGH
4 实验与分析
为验证本文所述的CGH 编码方法,设计了对比实验进行验证。所有元件加工完成后,对非球面进行检测。由于检测系统误差主要为CGH基底误差,因此,为了避免CGH 基底对检测产生的影响,利用零级衍射光对CGH 的基底误差进行标定,标定光路如图7 所示(图中虚线框代表将CGH 从标定光路取出的过程,TF(Transmission Flat)、RF(Reference Flat)为平面标准具),基底误差标定结果为:PV=24.361 nm,RMS=2.059 nm,如图8(彩图见期刊电子版)所示。
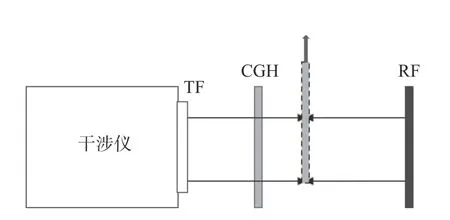
图7 标定光路示意图Fig.7 Schematic diagram of calibration optical path of the CGH substrate error

图8 CGH 基底误差Fig.8 CGH substrate error
完成CGH 基底误差标定后,利用如图9 所示的光路对非球面进行检测,非球面镜实物如图10 所示。实验过程中,通过观察干涉条纹实现各元件的对准。为了验证CGH 法检测非球面的可信度,本文使用零位补偿器对非球面进行检测,两者的检测结果如图11(彩图见期刊电子版)所示。从图11 可以看出,零位补偿镜的检测结果如下:PV 值为18.067 nm,RMS 值为3.645 nm,CGH的检测结果如下:PV 值为15.304 nm,RMS 值为3.142 nm,两者RMS 数值仅相差0.503 nm。将CGH检测结果与补偿镜检测结果进行点对点做差,结果如图12 所示。

图9 非球面检测装置光路图Fig.9 Optical path of the aspheric detection installation

图10 被检非球面镜Fig.10 Tested aspheric mirror

图11 两种方法的非球面检测结果对比Fig.11 The test results of the aspheric mirror by proprosed method and zero compensator

图12 CGH 与补偿镜检测结果对比Fig.12 Comparison of test results of CGH and null lens compensator
由图12 可以看出,CGH 法与补偿器法的检测结果相减后RMS 值为1.291 nm,各项Zernike系数差值均在0.002λ(λ=632.8 nm)以内,表明本文提出的CGH 编码方法能够实现非球面高精度编码。
5 结论
本文提出了一种基于CGH 相位梯度动态选择步长的编码方法,该方法能够有效解决传统编码方法的编码精度与编码数据量存在矛盾的问题,且能够满足非球面高精度检测的需求。本文设计、编码并制作了CGH 检测非球面,检测结果为3.142 nm(RMS)。为验证CGH 检测非球面结果的可靠性,本文将零位补偿镜对非球面的检测结果与CGH 检测结果进行对比,补偿镜检测结果为3.645 nm(RMS)。对CGH 和补偿镜的检测结果进行点对点做差,RMS 为1.291 nm,且各Zernike 项的差值都小于等于0.002λ,说明了该编码方法可满足非球面高精度检测的需求。
