面向天基引力波探测的时间延迟干涉技术

王登峰，姚 鑫，焦仲科，任 帅，刘 玄，钟兴旺

（中国空间技术研究院西安分院，陕西 西安 710100）

1 引言

基于迈克尔逊激光干涉仪的引力波探测器开启了人类观测宇宙的新纪元。2016 年以来，位于美国的臂长4 km 的LIGO 探测器和位于意大利的臂长3 km 的VIRGO 探测器联合探测到数十次致密双星的合并事件，自此引力波天文学得以迅猛发展。目前，地基引力波探测器已经持续运行数年，并且在不断改造升级以达到更高的灵敏度[1-3]。然而，受臂长限制，地基探测器的观测窗口在1 Hz 到kHz 的高频段。由于在地面大幅度增加干涉仪臂长是不实际的，并且存在难以消除的低频地表震动噪声，因此LIGO 等探测器无法有效观测到1 Hz 以下的低频引力波信号。另一方面，在mHz 波段宇宙存在着最丰富的引力波辐射源。在太空中构建具有十万公里甚至百万公里臂长的干涉仪是观测低频引力波的理想解决方案。欧洲主导的“激光干涉仪空间天线”（Laser Interferometer Space Antenna，LISA）项目便是瞄准探测和研究毫赫兹波段引力波辐射源的典型代表。在LISA 任务中，三颗全同卫星组成边长为5×106km（约16.67 光秒）的等边三角形，依靠三颗卫星间的激光链路实现低频引力波的观测[4-5]。2015 年12 月，欧洲航天局成功发射了一颗技术验证星LISA Pathfinder，验证了检验质量块的无拖曳控制技术的可行性[5-6]。2018 年，基于激光干涉测距的GRACE Follow-On 高精度地球重力场测量卫星发射成功，并在约220 公里的低跟踪双星编队间实现了纳米级的星间相对距离测量目标，验证了LISA 项目的部分关键技术[7]。最近几年，为了抢占引力波探测科学高地，中国科学院[8-12]和中山大学[13-15]也相应开启了天基引力波探测研究项目，分别命名为“太极”和“天琴”计划，并在2019 年相继成功发射了一颗技术验证星。

在天基引力波探测中，需要对自由悬浮的检验质量块间实现十皮米量级的位移测量精度。然而，受轨道动力学影响，三颗卫星编队之间的基线长度最大相差2%。因此，注入到迈克尔逊干涉仪两臂的激光源频率噪声无法互相消除，从而无法有效探测到引力波导致的质量块间皮米级的位移信号。另一方面，目前星载超稳晶振（Ultra-stable Oscillator,USO）的频率稳定度无法支持皮米级的甚高测相精度，USO 引入到相位计的噪声同样会导致无法有效探测到引力波信号。因此，激光源频率噪声和星载时钟频率噪声成为天基引力波探测任务中的两个主要问题。在2004 年发布的LISA 任务白皮书中，激光源噪声和时钟噪声消除问题位列69 项任务风险中的前两项。为了解决天基引力波干涉仪中激光源噪声无法直接消除的问题，J.E.Faller 等人首次提出了时间延迟干涉技术（Time Delay Interferometry,TDI）的概念[16]。在TDI 中，对测相数据进行适当的延迟处理和线性组合，通过数据后处理的方式构造出臂长相等的干涉仪，从而消除激光源频率噪声[17-18]。为了抑制相位计中的时钟频率噪声，M.Tinto 等人提出将时钟信号调制到激光相位上，利用新的拍频信号和测相值提取出时钟噪声，从而在TDI 数据组合中消除时钟噪声项[19-20]。在后续的实验论证阶段，加州理工大学喷气推进实验室（JPL）[21-23]和德国马普引力物理研究所下属的阿尔伯特-爱因斯坦研究所（AEI）[24-28]等研究机构结合LISA 的系统设计对TDI 技术做了一系列地面测试，初步论证了在激光链路上完成相对位移测量、绝对距离测量和时钟噪声转移的3 个功能，为天基引力波探测奠定了坚实的技术基础。

本文针对天基引力波探测TDI 技术进行了分析总结，组织结构如下：第2 节讨论激光源频率噪声对引力波探测的影响，分析了TDI 技术抑制激光源噪声的物理图景，并结合LISA 项目光路系统布局，给出了简要分析和相应的数据组合类型；在第3 节，针对测相处理中的时钟噪声问题，LISA 项目利用时钟边带调制的方案，消除了TDI数据组合中的时钟噪声项；第4 节针对TDI 数据处理过程中对星间绝对距离的测量需求，讨论了星间激光链路的附加功能：伪随机码测距和数据传输；在文章的最后一部分，概述了针对TDI 技术的地面测试论证工作。希望对我国天基引力波探测任务以及其它激光干涉测量项目提供借鉴。

2 TDI 数据组合方式

2.1 需求分析

如图1 所示，在天基激光干涉仪中，卫星1 上的激光经过分束镜分束后分别注入到干涉仪两臂L2（卫星1 和3 之间）和L3（卫星1 和2 之间）中。激光经过长距离传输后到达远星处的检验质量块处，被锁相放大后传送回来，在卫星1 上的分束镜合束后进入探测器。引力波会导致检验质量块产生微小位移，探测器将测量到激光干涉信号发生相位涨落。

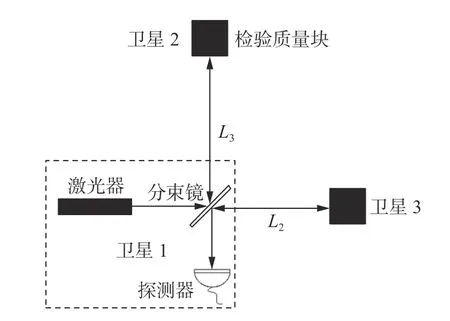
图1 天基迈克尔逊干涉仪Fig.1 Space-based Michelson interferometer

然而，由于受轨道动力学影响，三星编队之间的基线会有一定的差别。如在LISA 任务中，三星编队的中心位于日地轨道，编队基线的差别最大可达2%。因此，激光源注入到两臂的频率噪声无法在探测器处相互抵消。这样，激光源引起的频率噪声会淹没掉引力波信号引起的相位涨落。

对于迈克尔逊干涉仪而言，星间位移测量精度为：

2.2 TDI 物理图景

时间延迟干涉技术采用数据后处理的方式构造出虚拟的等臂长干涉仪。例如，在图1 中，激光先经过L2臂的往返，再经过L3臂的往返，相当于激光在虚拟干涉仪的一臂上传输。类似地，同一激光源产生的激光先经过L2臂的往返，再经过L3臂的往返，相当于激光在另一臂上的传输。这样，虚拟干涉仪的两臂臂长均为L2+L3，因此克服了卫星基线长度不相等的问题，实现了消除激光源频率噪声的目标。

具体而言，在卫星1 处，有两个探测器，分别记录本地激光与经过L2（L3）往返的激光干涉后的相位测量值：

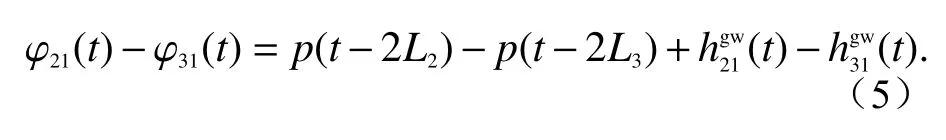
如前所述，L2和L3最大相差2%，因此，两臂上的激光相位噪声无法相消，参考目前的星载稳频激光源的噪声水平和天基引力波探测的灵敏度要求，式（5）中的相位噪声项将会淹没掉引力波信号。

在TDI 技术中，为了消去激光源相位噪声，对获得的测相值进行时间延迟处理，即在时间轴上进行平移。具体而言，对φ21(t)延迟2L3秒，对φ31(t)延迟2L2秒，有：

进一步比较式（5）和式（8），两式均包含相同的激光相位噪声项，因此通过式（5）与式（8）相减，可以得到一组含有引力波信号而不含有激光源噪声的数据组合，即：

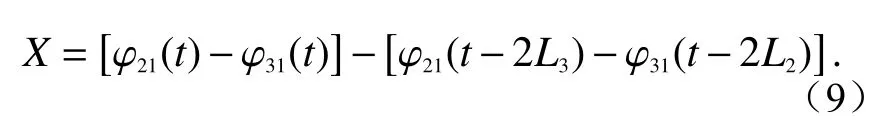
为了更好地理解TDI 数据组合背后的物理思想，将式（9）重新写作：

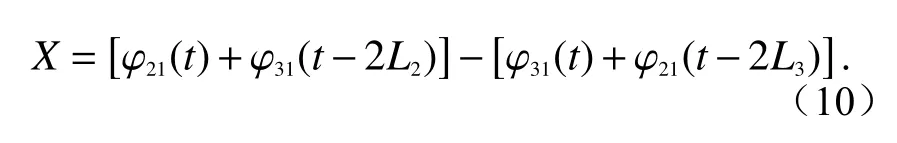
式（10）中[φ21(t)+φ31(t−2L2)]表示一束激光从卫星1 处出发，先经过L2臂的往返后与本地激光进行干涉，随后再经过L3臂的往返后与本地激光进行干涉，如图2 左图所示。其中，φ31(t−2L2)指经过2L2秒延时后的相位测量值。类似地，[φ31(t)+φ21(t−2L3)]表示一束激光从卫星1处出发，先经过L3臂的往返后与本地激光进行干涉，随后再经过L2臂的往返后与本地激光进行干涉，如图2 右图所示。这两种情况对应激光均经过了2L2+2L3的传输，相当于构造出臂长均为2L2+2L3的迈克尔逊干涉仪，从而实现了激光源相位噪声的消除。

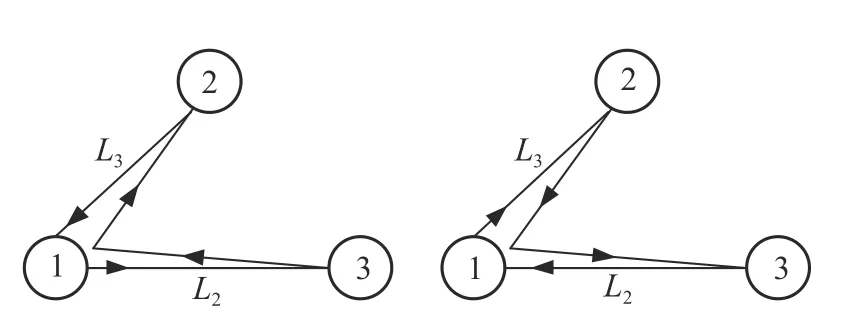
图2 TDI 原理示意图Fig.2 Diagrams of TDI principles

可以看到，TDI 技术实际上是对星间相位测量值进行适当的延时处理，再进行数据组合，构造出臂长相等的干涉仪，从而消除激光源相位噪声。

2.3 LISA 光学系统布局

为了给出TDI 的具体数据组合方式，以及方便下一节讨论时钟噪声的消除原理，这里以LISA项目为例，简要讨论天基引力波探测的光学系统布局。如图3 所示，LISA 星座中每一颗卫星均包含有两个光学平台。如图3 插图所示，在卫星i处，当面对三星编队中心时，左手处的光学平台定义为i号平台，右手处的光学平台定义为i*号平台。卫星i与卫星j之间的距离定义为Lk。在卫星i处，定义本地激光与远星处经过Lj传输的激光干涉后的相位测量值为 φji。另外，在同一光学平台上，还存在本地激光与相邻光学平台之间的激光干涉测量 βji。这样的下标命名规则是为了在得到一个卫星上的所有物理量表达式后，通过下标变换的方式，将表达式中下标“1”变为“2”，“2”变为“3”，“3”变为“1”，即“1 →2 →3 →1”式的下标循环变换，就能够直接得到其它卫星上相应物理量的表达式。

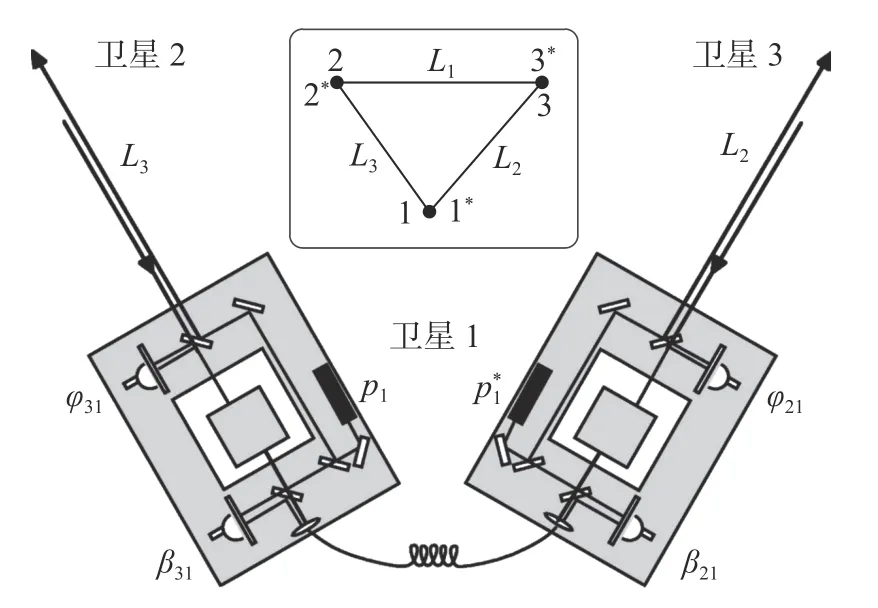
图3 LISA 光学系统示意图（已获参考文献[19]授权©American Physical Society）Fig.3 The illustration of optical system in the LISA mission(Reprinted with permission from ref.[19]©American Physical Society)

对于φ31，有：

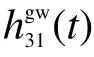
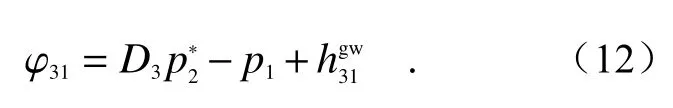
对于卫星1 内部相邻光学平台间的干涉测量β31，有：

这里相邻光学平台之间的链路延迟较小，不考虑。同时，忽略了光学平台噪声和检验质量块噪声，以及光纤链路噪声。

同理，对于φ21而言，有：

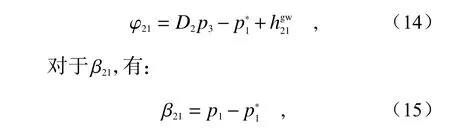
在得到了卫星1 的4 组相位测量的表达式后，通过“1 →2 →3 →1”下标循环变换，就可以得到其它两颗卫星上的8 组测相表达式。

2.4 TDI 数据组合方式

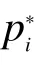
同时，由于数据组合的目标是消除激光相位噪声项，因此忽略引力波信号和其它噪声项，6 组测相值φij可以写作：

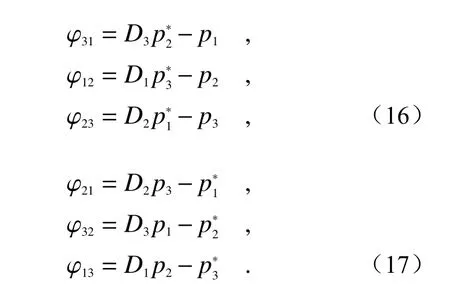
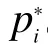
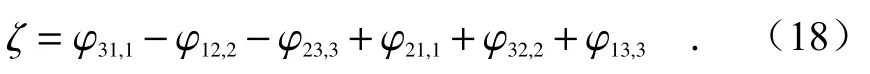
为了简便起见将延迟算符写入下标，例如将D1φ31项写作 φ31,1。

第二类解称为α 型数据组合：

通过“1 →2 →3 →1”下标变换，还可以得到两个新的数据组合，它们实质是等价的。

上述两类解累计施加了6 次时间延迟算符。除了这两类最简单的解，还存在一类常见的解，称为不等臂迈克尔逊数据组合，习惯称为X型数据组合：

同样地，对X型数据组合进行下标循环变换，可以得到等价的Y型和Z型数据组合。

虽然对比前面的 ζ型和 α型数据组合，X型数据组合累积施加了12 次时间延迟算符，然而，X型数据中不包含卫星2 和卫星3 间的干涉测量值，即 φ12和 φ13，也不需要施加这两颗卫星间的链路延迟算符D1。因此，三星编队中某一条星间激光链路建立失效的情况下，X型数据组合仍然可以正常工作。因此，相比 ζ型和 α型数据组合。X型数据组合提升了系统冗余性，并且减少了对星间链路L1的测距需求。实际上，X型数据组合背后的物理模型与上一节中的图2 类似。

具体而言，式（20）中X型数据组合的前4 项对应图4 左图，即激光沿①-②-③-④路径传输的过程。例如，φ21对应激光从卫星3 出发，经过星间链路L2后，到达卫星1 与本地激光干涉。而第二项 φ23,2对应经过L2秒时间延迟后的干涉测量，即φ23,2是紧接着 φ21进行的。以此类推，φ31,22和φ32,322分别对应接下来的图4 左图的③和④。类似地，式（20）后4 项对应图4 右图的传输路径。可以看到，X型数据组合对应两臂臂长均为2L2+2L3的迈克尔逊干涉仪的测量结果，因此激光源的相位噪声被消除。

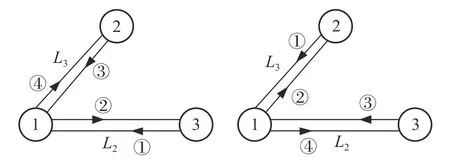
图4 X 型数据组合物理模型Fig.4 The physics modal of the X type data combination

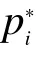
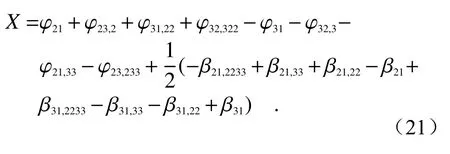
可以看到，TDI 通过对各个卫星平台上的单程测相值进行时间延迟和线性组合，构造出等臂长的迈克尔逊型或萨格纳克型干涉仪，从而消除激光源频率噪声。

2.5 第二代TDI 数据组合

前面关于TDI 的讨论主要基于星座和臂长均处于静态的情况。实际上需要考虑星座旋转和臂长变化的情况，从而形成第二代TDI 数据组合方式。

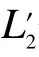
图5 当星座旋转时，≠LiFig.5 In the case of the constellation rotation,≠Li

3 时钟噪声消除

3.1 需求分析

在相位测量系统中，时钟频率（相位）抖动会引入到测相误差中。因此，需要评估在甚高测相精度要求下，时钟频率稳定度需要达到的水平。

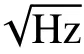
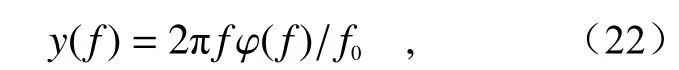
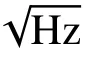
3.2 时钟边带调制

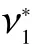
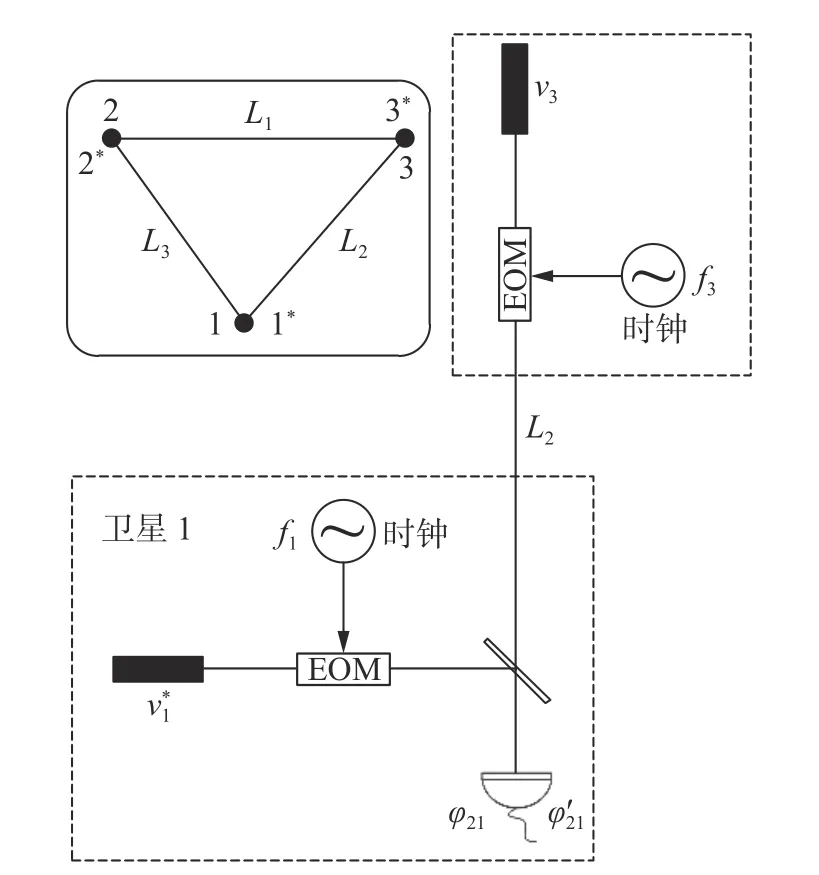
图6 时钟边带调制示意图。EOM：电光调制器Fig.6 Schematic diagram of clock sideband modulation.EOM:Electro-Optic Modulator

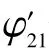
3.3 时钟噪声消除原理

本小节以X型数据组合为例，具体阐述时钟噪声消除的原理。图7 是图6 探测端的信号处理示意图。这里进一步考虑了星间多普勒频移。

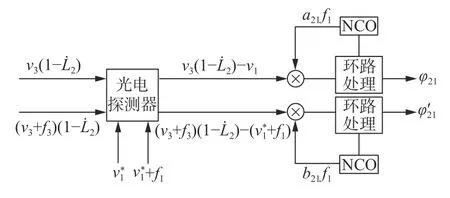
图7 探测端信号处理示意图。NCO：数控振荡器Fig.7 Signal processing illustration of photon detection.NCO:Numerically Controlled Oscillator

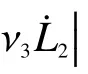
具体地，载波相位输出值φ21的表达式为：

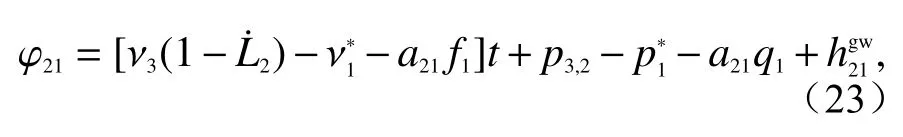
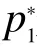
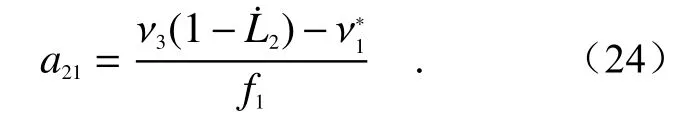
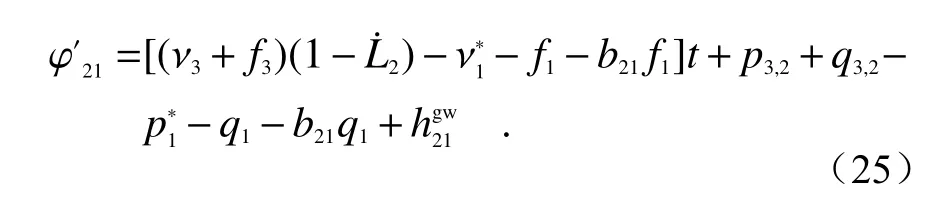
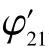
通过下标循环变化“1 →2 →3 →1”，就可以得到其它两颗卫星上的4 组表达式。

对于式（21）所示的X型数据组合，当考虑如式（23）所示的时钟噪声项qi后，包含时钟噪声的Xq表达式为：

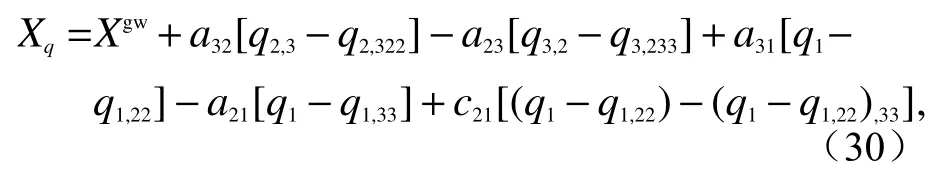
其中，c21为卫星1 的1*号平台处 β21探测器（图3）后端NCO 的输出系数：

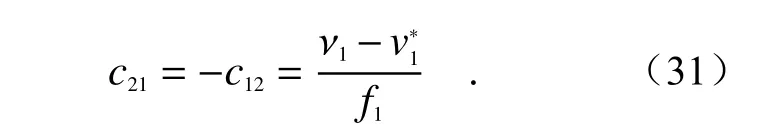
通过ri j可以得到Xq式中[q2,3−q2,322]等项表达式：

利用上述关系式减去时钟噪声项，得到修正时钟噪声项的X型数据组合：

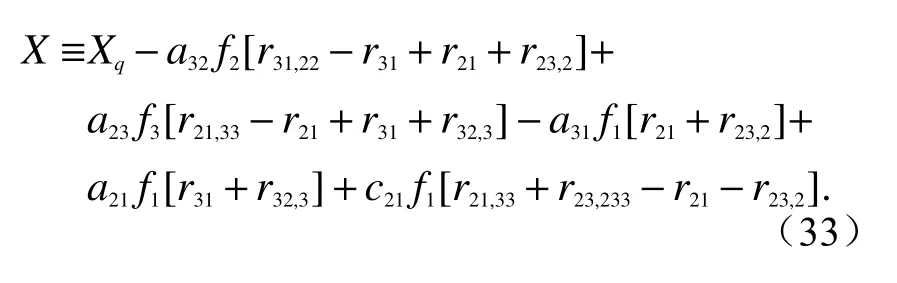
可以看到，时钟调制产生了边带拍频信号，通过与载波拍频信号作差得到rij，提取出时钟噪声因子，从而能够减去TDI 数据组合中的时钟噪声项，最终消除时钟噪声。值得注意的是，上述时钟噪声消除仅针对静态的第一代TDI 数据处理方式。由于时间延迟算符的非对易性引入的时钟相位噪声可以忽略不计，因此在第二代TDI 数据组合中，也可以采用类似的处理方法，消除相应的时钟相位噪声项[20]。

3.4 模数转换噪声抑制

在天基引力波探测中，为了实现1 0−6周的甚高测相精度，除了时钟相位噪声问题，还需要重点考虑模 数转换（Analogue to Digital Conversion,ADC）过程引入的相位噪声。ADC 噪声主要有量化噪声和采样时间抖动噪声。其中，量化噪声可以忽略不计，而采样时间抖动噪声由ADC 器件本身的孔径抖动和外部的采样时钟抖动构成。为了消除采样时间抖动噪声，一种方案是从时钟处引出一路导频（Pilot Tone）信号，令导频信号经过ADC 器件[33-34]，导频信号通过数字锁相环路处理后可读出相应的相位增量。假设导频信号的频率fpilot非常稳定，那么理想的相位增量fpilot∆T是恒定的。这里，∆T是相位读取周期。然而，测量得到的导频信号相位增量会由于ADC 采样时间抖动而在fpilot∆T附近抖动，相应的偏差δφdet即为该ADC 器件由于采样时间抖动引入的测相噪声。对于同样经过该ADC 器件采样处理的拍频信号fbeat，添加相位纠正项δφdetfbeat/fpilot，即可消除ADC采样时间抖动引入的测相噪声。然而，导频方案的问题在于，USO 有限的频率稳定度会导致fpilot∆T本身不是恒定值，因此会导致δφdet不仅包含ADC 采样时间抖动因素，还包含了时钟相位噪声qpilot。由于时钟相位噪声与时钟信号的频率成正比，因此可以将qpilot添加到前述测相表达式中。例如，在3.3 小节中，1 星上频率为f1的时钟信号的相位噪声为q1，其通过导频纠正方案引入的时钟相位噪声项为qpilot=q1fpilot/f1。将其添加到测相表达式中，随后再进行相应的时钟相位噪声消除处理。可以看到，抑制模数转换噪声的导频方案需要在时钟噪声消除的基础上实现，凸显了时钟噪声消除方案的重要性。

4 绝对距离测量

4.1 需求分析

在TDI 的数据处理和重组中，为了消除激光源和时钟频率（相位）噪声，关键在于对相位测量值进行精确的时间延迟处理，这就要求对天基干涉仪的臂长，即星间距离有精确的认识。从这个角度看，TDI 技术抑制激光源和时钟噪声的前提是需要对星间绝对距离进行一定精度的测量。

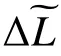
4.2 编码参数设计

在LISA 项目中，采用直接序列扩频进行数据传输和测距编码。数据码采用BPSK 编码，对伪随机码扩频后用于进行绝对距离测量。如图8所示，数据码和伪随机码构成的扩频码与时钟信号一同加载到载波激光相位上。类似于时钟信号的浅相位调制，扩频码的相位调制系数也很低，将消耗1%左右的载波功率。

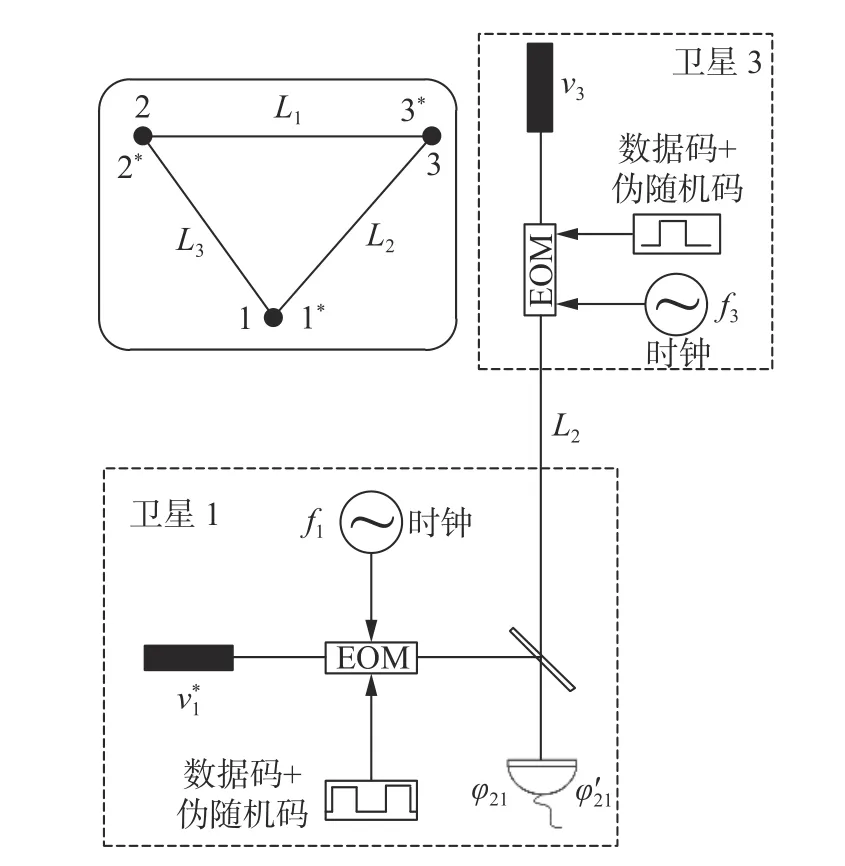
图8 在载波相位上调制数据码和伪随机码用于星间数据传输和绝对距离测量示意图Fig.8 The phase of the carrier is modulated by data codes and pseudo-random codes for the inter-satellite data transmission and absolute distance measurement

图9 是LISA 项目扩频码的参数设计示意图。上层的数据码调制速率为24 kbps，对应的码周期为40.96μs。底层的伪随机码调制速率为1.5 Mbps，码片周期为640 ns。伪随机码序列的重复频率为1.5 kHz，每段序列包含1 024 个伪随机码码片。因此，伪随机码序列覆盖的测距长度为200 km，测距信息刷新频率为1.5 kHz。对于LISA 星座500 万公里的星间距离，需要一个精度优于200 km 量级的初始定位系统。深空网络结合每颗卫星上的恒星追踪器可以提供精度约为25 km 的星间距离粗测量。经过初始定位后，就可以利用伪随机码来提供更精准的距离测量。

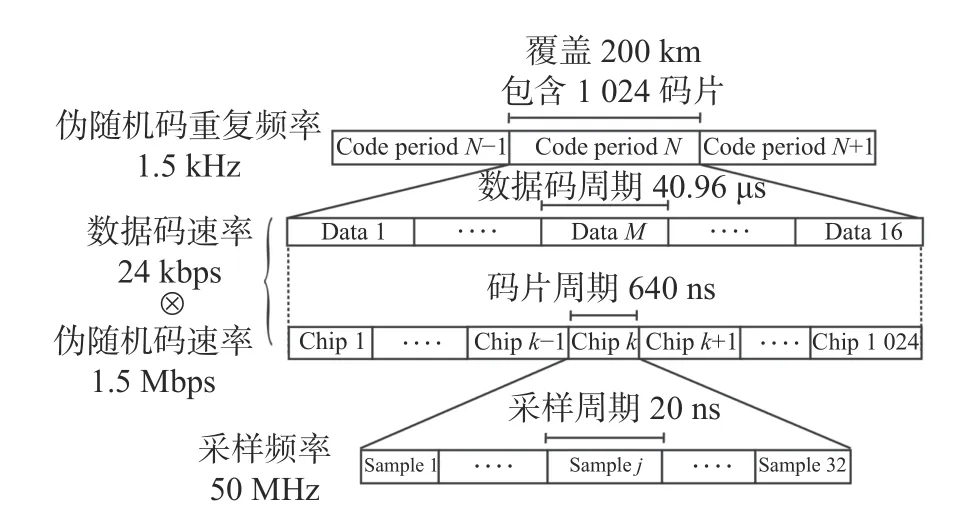
图9 数据码和伪随机码参数设计流程（已获参考文献[24]授权©The Optical Society）Fig.9 Flow chart of parameter design of data codes and pseudo-random codes(Reprinted with permission from ref.[24]©The Optical Society)

德国阿尔伯特-爱因斯坦研究所（AEI）针对时钟噪声转移和伪码测距等技术进行了一系列地面论证实验。图10 是在光载波上调制GHz 时钟频率和MHz 扩频码的干涉测量结果。扩频码调制深度为0.1 rad，时钟边带调制深度为0.45 rad，分别约消耗1%和10%的光载波功率。

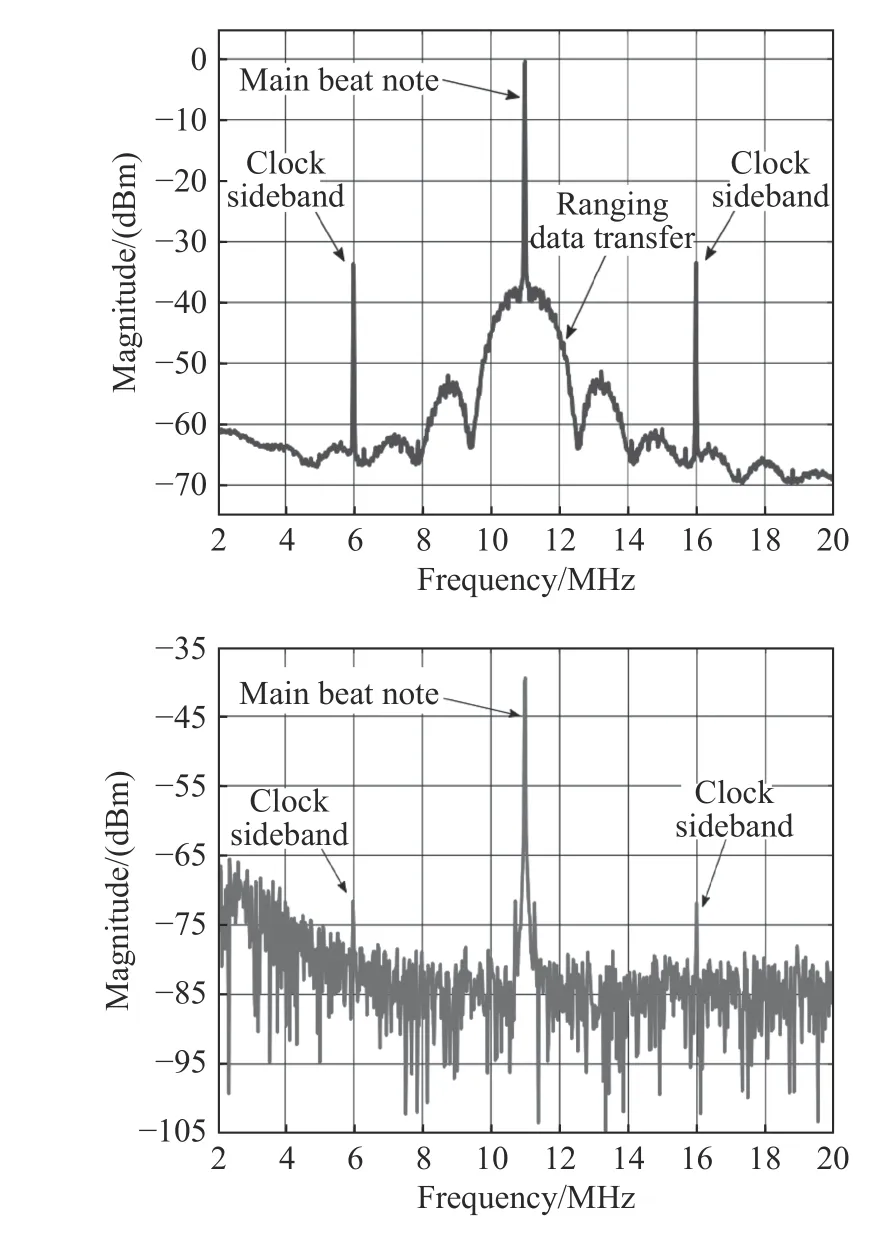
图10 光载波经过时钟信号和扩频调制后的干涉测量结果（已获参考文献[24]授权©The Optical Society）Fig.10 Interference measurement results when the optical carriers are modulated by the clock signal and broaden spectrum(Reprinted with permission from ref.[24]©The Optical Society)

图10 上图是强光条件下的测试结果，中间的信号峰为载波拍频信号，附近则是扩频频谱。由于两台激光源的时钟调制频率相差5 MHz，因此在距离载波拍频峰±5 MHz 处会出现时钟边带的拍频信号。图10 下图是模拟天基引力波环境下的100 pW 弱光探测结果，对应的扩频码所占功率仅为1 pW。在散粒噪声较大的情况下，模拟星上3 Hz 伪码延时锁定环测量带宽，系统的测距均方根误差为42 cm，优于1 m 的LISA 任务绝对距离测量要求。另外，数据传输的误码率为26×10−3，应用前向纠错编码可使误码率进一步降低到可实际应用的10−9水平。

值得注意的是，目前的伪距测量论证实验是在静态条件下完成的。在实际的在轨测距中，由于星间链路延时达数十秒，而星间相对运动速度在10 m/s 量级，因此，需要考虑在激光传输过程中卫星相对运动造成的测距误差。

5 TDI 技术实验论证

加州理工大学喷气推进实验室（JPL）针对TDI 技术的激光源噪声和时钟噪声消除进行了地面验证实验。图11 是在0.2 mHz 到3 Hz 频段几种测量方式的位移测量噪声线性谱密度对比情况[22]。由于激光源中心波长为1 064 nm，因此1μcycle≈1 pm。

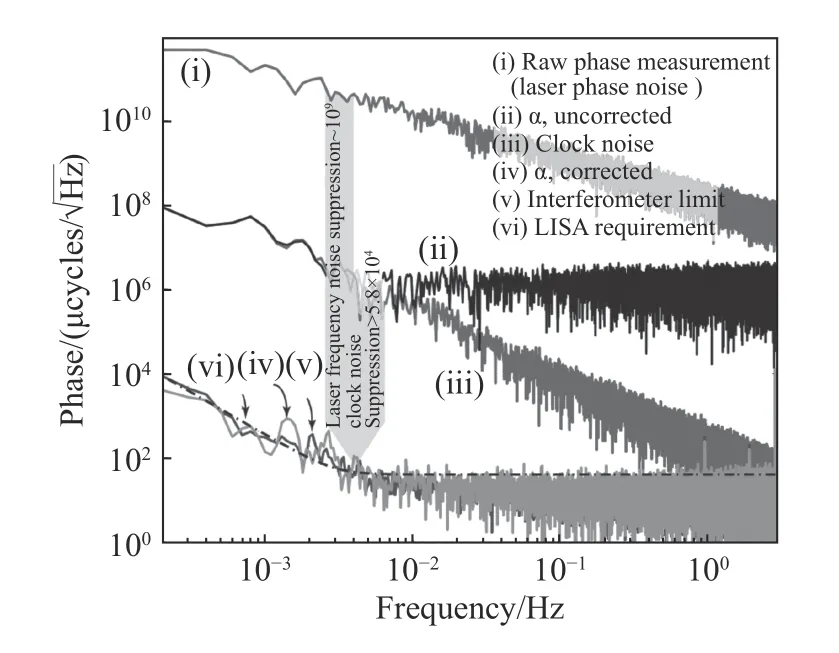
图11 LISA 干涉仪测试床位移测量结果（已获参考文献[22]授权©American Physical Society）Fig.11 The displacement measurment results in the LISA interferometry test bed(Reprinted with permission from ref.[22]©American Physical Society)

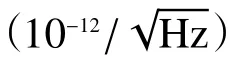
与JPL 实验室放置在真空腔内的短臂长干涉仪不同，科罗拉多大学博尔德分校的S.E.Pollack 等人[35-36]和法国巴黎狄德罗大学的P.Prat 等人[37-38]分别开发了小型的桌上电光系统，用来模拟LISA 星座中的大范围光学传播时延和星间多普勒频移，以验证相位计与探测器等硬件部分和TDI 算法的可靠性。S.E.Pollack 等人搭建了一套LISA 地面测试平台[35]，用来生成接近实际在轨情况的激光干涉条纹，例如拍频信号频率从50 kHz 变化到15 MHz，并加入了星间多普勒频移的变化速率以及加速度。干涉信号由100 pW量级的弱光与0.5 mW 激光干涉产生，模拟了星间远距离传输来的激光与本地激光的干涉测量。实验论证了过零点计数相位计的有效性，证明TDI 算法可对模拟产生的激光相位噪声进行有效消除。进一步地，他们在测试平台上通过相位浅调制在激光链路上附加了数据传输和时钟边带调制功能，验证了包含科学测量信号的主拍频信号与链路附加信号互不干扰[36]。P.Prat 等人搭建了了一套光电模拟系统[37-38]。该模拟系统具有光学模拟信道和电子模拟信道，用于产生激光拍频或射频间的混频信号，并最终进入相位计模块进行测相和数据处理。由于采用TDI 中的X型数据组合方式，因此只需要模拟两条激光链路上的干涉测量即可。在电学模拟实验中，由直接数字信号合成器（DDS）产生3 个100 MHz 左右的射频信号。通过射频信号之间的混频来模拟星间激光干涉拍频信号。通过设置射频信号的相位噪声和时间延迟来模拟LISA 中的噪声和链路时延。通过TDI 技术使得信号噪声降低了109倍。在光学实验系统中，采样声光调制器（AOM）对激光链路进行移频的方式模拟星间多普勒频移。通过TDI 技术使得光学信号的噪声降低了5×107倍。光学信号的降噪倍数较低，原因在于激光传输路径上存在光程抖动因素。另外，APC 实验室还在相位计的ADC 端口添加了如3.4 小节所述的导频纠正方案。后续的工作中，APC 实验室将考虑链路时延和多普勒频移随时间变化的情况，以使得光电模拟信道更加逼近真实在轨情况。

6 结束语

对基于天基激光干涉仪的引力波探测项目具有极高的灵敏度探测要求，这将极大推动星载激光收发终端和星间激光链路指向控制等研究方向的技术进步，并孵化出面向高精度地球重力场测量的激光干涉测距载荷。针对十皮米量级的高精度星间位移测量要求，需要首先解决激光源频率噪声和时钟频率噪声的问题。TDI 技术利用对三星编队上的多组测相值进行延时处理和线性组合，构造出了等臂长干涉仪，从而消除了激光源噪声。结合星间绝对距离1 米的测量目标，将抑制激光源噪声要求定为8 个数量级。为了消除时钟噪声，通过时钟边带调制方案产生新的拍频信号和测相值，并通过对测相值作差提取出时钟噪声项，用于修正TDI 数据组合，将目前的星载时钟噪声抑制3 个数量级。由于在降低测距误差中消除激光源噪声和时钟噪声具有最高的优先级，因此，TDI 数据处理方式将成为未来引力波探测的核心机制。另外，TDI 技术对我国下一代基于激光干涉测距的重力场测量卫星载荷的研发也具有重要的参考价值。实际上双星激光干涉测距采用的锁相转发机制能够等价为两组单向测相值的TDI 数据组合[39]，进而可以降低光学锁相精度要求。可以看到，开展TDI 方面的深入研究对我国未来开展包括引力波探测在内的天基激光精密测量具有重要价值。