表面织构分布参数对流体动压润滑的影响及其数值优化*

黄丰云 杨晓兵 朱继伟 徐劲力

(武汉理工大学机电工程学院 湖北武汉 430070)

近年来,表面织构技术已被证明是改善摩擦副摩擦学性能的有效手段[1-3]。表面织构技术就是在摩擦表面加工出具有一定尺寸参数、几何形貌和排列方式的微凹坑，当摩擦副相对运动时，由于微凹坑的楔形效应使相对运动表面间产生附加流体动压力，使得摩擦副之间几乎不直接接触，从而产生流体动压润滑[4]，起到增加油膜承载力，减小摩擦磨损的效果。

研究表明，表面织构的几何形貌和参数是影响摩擦副摩擦学性能的主要因素，通过理论和实验的方法优选合理的表面织构几何参数和分布间距，能够使织构表面产生最佳的油膜承载力和润滑性能。JI等[5]研究了抛物线槽、矩形槽和三角形槽形式的部分表面纹理对流体动压力的影响,结果表明，凹槽的几何形状、面积密度、沟槽深度和方向对流体动压力有明显影响。于海武等[6]选取圆柱形微凹坑，研究了织构面积率、深度、直径、深径比等参数对织构表面润滑性能的影响，并且得到了微凹坑的最优几何参数。陈小兰等[7]、孙子炎[8]基于雷诺方程建立椭圆形微凹坑流体动压润滑模型，分析了椭圆凹坑的倾角、长短轴比、深度、面积率及等效半径对平均润滑膜压力的影响。国内外从几何参数和分布形式方面对表面织构做了相应的研究，但大多以正方形织构单元[9-13]为研究对象，且织构的分布密度或间距在水平和垂直方向上均相等，而针对不等边织构计算单元的研究较少，并且仅研究了分布参数对油膜压力的数值影响，很少涉及织构分布参数对油膜压力一致性和稳定性的影响。

本文作者针对球冠形凹坑织构，选择不等边计算控制单元，模拟凹坑横纵向分布间距不同的情况，基于多重网格法对控制区域求解Reynolds方程，以平均油膜压力作为评价指标，研究表面织构分布间距对油膜压力数值大小的影响，计算出表面微凹坑的最优分布间距，并且基于CFD获得分布间距变化下控制区域的流体迹线图，研究其对油膜压力的影响机制，同时选择5×5的织构模型，分析凹坑分布对织构中心线上油膜压力峰值的影响。

1 数学模型的建立

表面织构的压力呈周期性分布，为了提高计算效率，可以选择一个凹坑控制单元作为计算域。 由于球冠形凹坑织构有良好的各向同性性能，并且相比于圆柱形、三角形、菱形等织构可以获得更优越的润滑性能[14-15]，因此文中选取球冠形的单凹坑织构模型的控制单元为研究对象。假设上表面为光滑表面，下表面为具有球冠形凹坑分布的表面，上表面以一固定的速度U相对于下表面作平行运动，取凹坑深度为hp，凹坑半径为r，控制单元设置为Lx×Ly的矩形，假设摩擦副的两表面被一层润滑膜完全分离，即最小油膜厚度为h0，织构模型如图1所示。

图1 织构模型示意

为简化模型，做以下基本假设：①沿润滑油膜厚度方向，不考虑油膜压力的变化；②流体为不可压缩的牛顿流体层流流动，即流体密度为常量，忽略流体的密压特性；③忽略流体惯性力和黏性力的影响；④流体的黏度和温度保持恒定，即忽略流体的黏压特性和黏温特性；⑤流体在摩擦表面上无相对滑动;⑥摩擦副处于全膜润滑状态。

由上述简化可得表面织构流体动压润滑的二维Reynolds方程如下：

(1)

式中：x、y为控制区域的节点坐标；p为流体动压润滑产生的油膜压力；h为油膜厚度；U为摩擦副上表面的运动速度；μ为润滑油的动力黏度。

膜厚方程为

h=

式中:η=(x-Lx/2),ξ=(y-Ly/2)。

为了消除数值间的差异大小，减少计算矩阵的奇异性，减少计算误差，使数值计算的结果不受单位限制，增加解的通用性，需对上述方程中的变量进行量纲一化处理。控制方程量纲一化方法参考文献[16]，各参数定义如下：

x=X·r,y=Y·r,h=H·h0,p=P·p0

(3)

将式(3)代入式(1)中可得量纲一化后的Reynolds方程和膜厚方程分别为

(4)

(5)

在求解时，边界条件是控制方程有确定解的前提，求解上述方程时，需要设置合理的压力边界条件使计算结果更加符合实际情况。在计算时，取控制区域边界的压力为环境压力：

P(X,0)=P(X,Ly)=P(0,Y)=P(Lx,Y)=P0

(6)

同时由于在摩擦副之间存在收敛间隙和发散间隙，所以在计算中会出现负压情况，而实际中润滑膜无法承受负压将会导致油膜破裂出现空化现象，从而避免正负压相抵消影响动压的产生。Reynolds空化边界条件较其他边界条件有较高的计算精度和计算速度，所以引入Reynolds空化边界条件，即在油膜破裂区油膜压力设为环境压力，压力梯度置零。

(7)

2 模型的求解

2.1 数值求解

在求解二维偏微分的Reynolds方程时，需要将方程离散化，将其转化成线性方程组进行求解，采用有限差分法[17]离散控制方程，可得差分方程为

APi+1,j+BPi-1,j+CPi,j+1+DPi,j-1-EPi,j=F

(8)

其中，

采用四层网格、W循环的多重网格法[18]和超松弛迭代法进行求解，即可求解出控制区域离散节点上的油膜压力分布；利用式(9)计算出控制区域的量纲一平均油膜压力Pav，作为评价摩擦副润滑性能的指标，并分别改变表面凹坑的几何参数，来研究量纲一平均油膜压力的变化情况。

(9)

2.2 参数选择

润滑油在摩擦副间的流动遵循Navier-Stokes方程，而润滑计算中广泛采用的Reynolds方程是N-S方程针对润滑问题的简化形式，忽略了惯性项的影响和油膜厚度方向压力梯度的变化。但在油膜厚度和雷诺数过大时，对于表面织构润滑计算模型的建立求解，上述影响是不可以忽略的，因此在选择织构参数时需要考虑Reynolds方程的有效性，减小惯性项和油膜厚度方向压力梯度变化对计算结果的影响，减小方程相较于N-S方程的计算误差。评价表面织构动压润滑计算有效性的2个关键因素[16]为油膜厚度与纹理特征长度的比值δ和缩减的雷诺数Rer:

(10)

式中：L为计算单元在x方向上的长度尺寸,即纹理特征长度Lx;Re为雷诺数。

对于球冠形凹坑，Reynolds方程有效性的评价标准[19-20]如下式所示：

(11)

根据上述评价标准,可取织构参数如表1所示。

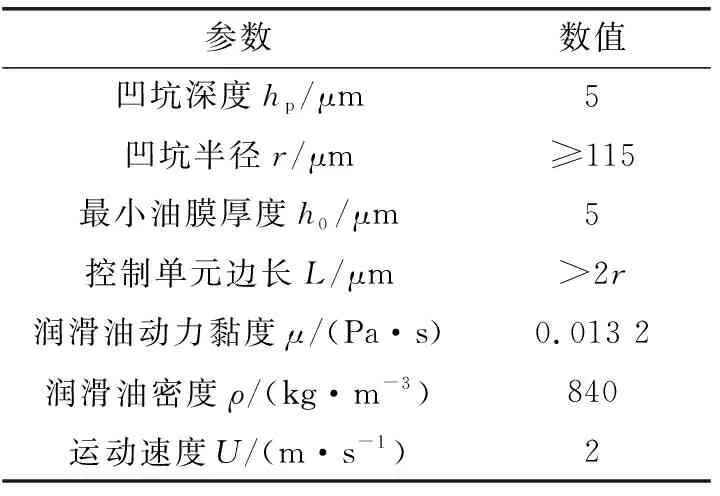
表1 表面织构计算参数

3 结果与讨论

3.1 凹坑分布间距对量纲一平均油膜压力的影响

为了更加直观地表示控制区域油膜承载力随凹坑分布间距的变化情况，改变控制单元的边长来模拟凹坑分布间距的变化。考虑Reynolds方程有效性，选择最小油膜厚度h0为5 μm，凹坑深度hp为5 μm，分别取凹坑半径r为115、125、135和145 μm时，得到图2所示的量纲一平均油膜压力随控制单元边长的变化曲线。可以看出平均油膜压力随着控制单元边长的增大，先迅速增大，之后缓慢减小，在控制单元边长L大约为凹坑半径的3.4倍时，即凹坑面积占有率为0.272，凹坑分布间距L为3.4r时，平均油膜压力可达到最大值。同时可以观察到较大半径的凹坑能够产生更大的油膜承载力，控制区域大小对油膜平均压力的影响程度随着凹坑半径的增大而逐渐增大。

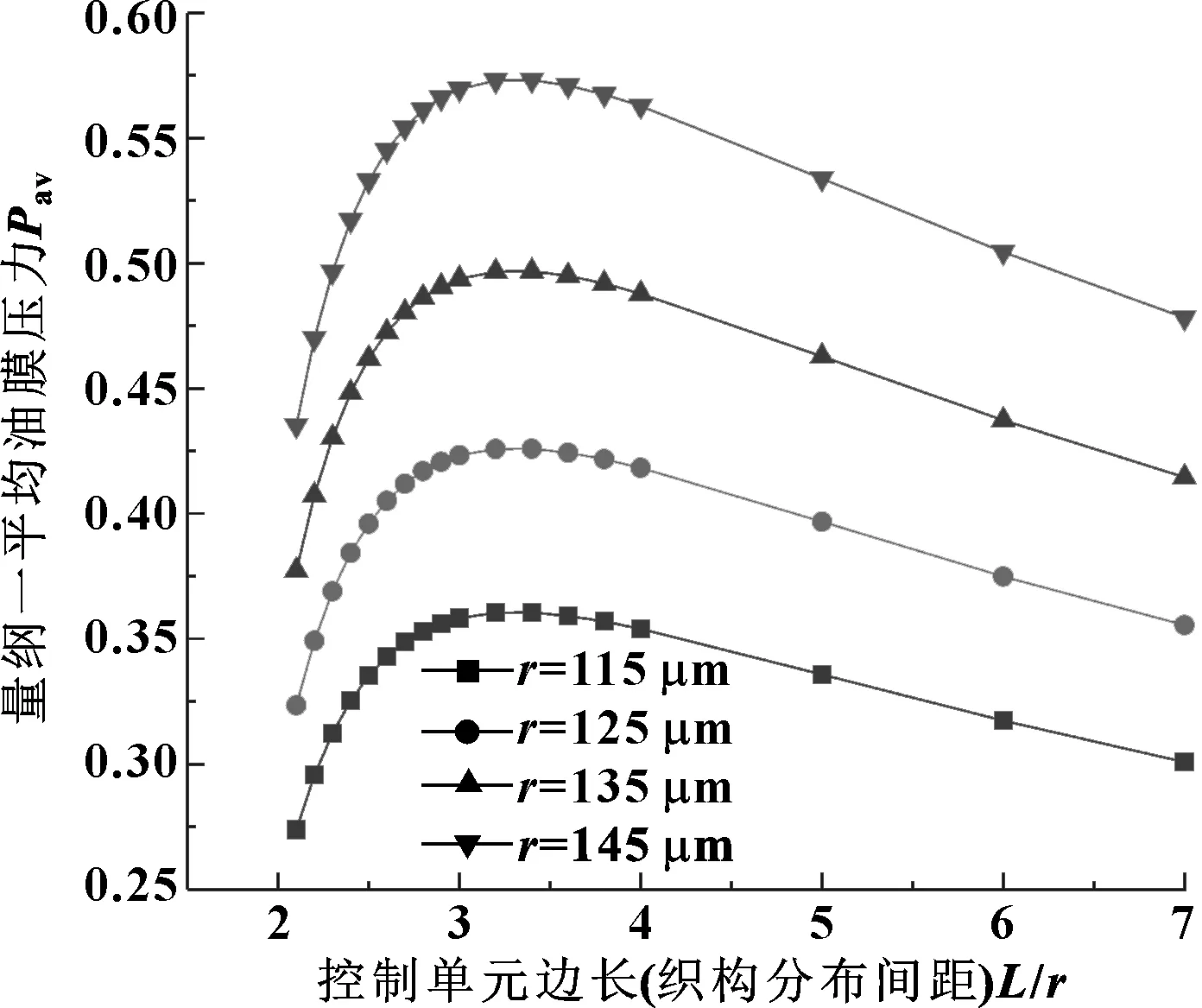
图2 量纲一平均油膜压力与凹坑分布间距的关系曲线(h0=5 μm,hp=5 μm,U=2 m/s,δ≤0.021，Rer≤0.013)

上述研究讨论了控制单元为长宽相等的正方形单元，即凹坑横向和纵向分布间距相同时的平均油膜压力分布情况，但未考虑表面凹坑横向和纵向分布间距不等时的油膜承载力情况。因此选取固定的控制单元宽度Lx=3.4r和不同的凹坑半径r，通过改变控制单元的长度Ly，模拟凹坑横向和纵向分布间距(密度)不同时的油膜压力情况。其中，Lx为润滑液流动方向的控制单元边长，Ly为润滑液流动方向法向的控制单元边长。从图3(a)可以看出，不同凹坑半径下，平均油膜压力的变化趋势与正方形等边控制单元油膜压力分布趋势基本一致，平均油膜压力随着控制单元的边长Ly的增大先增大后减小，存在一个最优的Ly，使得油膜压力达到最大值，不同的是，平均油膜压力的最大值出现在Ly为2.8r即Ly/Lx为0.82左右，此时获得了比Ly/Lx=1时，即控制单元长宽相等时更大的平均油膜压力。

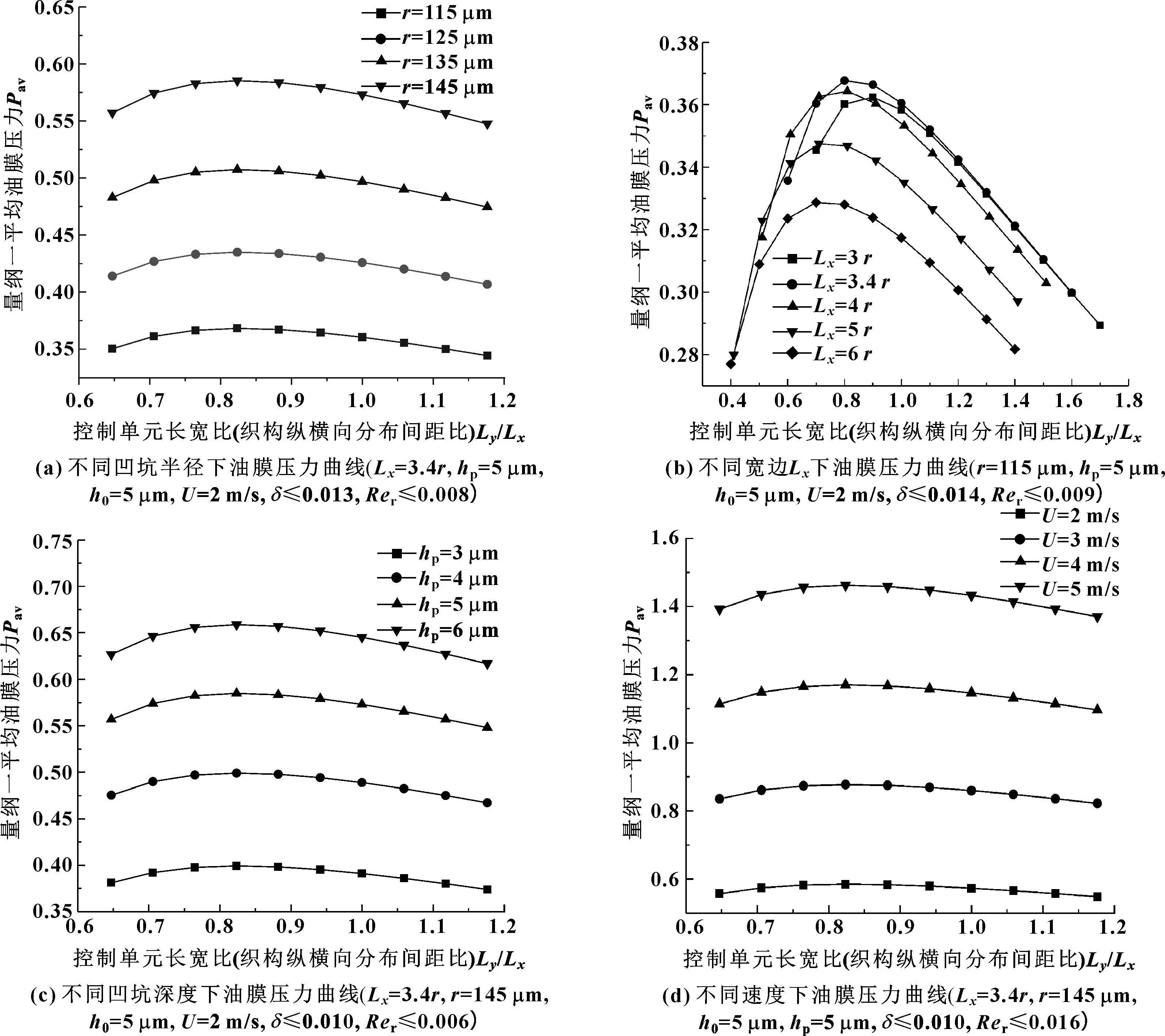
图3 量纲一平均油膜压力与控制单元长宽比关系曲线

选择凹坑半径为115 μm，分别选取几组不同控制单元宽边Lx，然后改变控制单元长宽比，研究不同控制单元宽边Lx下，量纲一平均油膜压力随控制单元长宽比的变化情况，得到量纲一平均油膜压力与控制单元长宽比关系曲线如图3(b)所示。显然，不同的凹坑宽度下，都存在一个最优的长宽比，使油膜承载力达到最大。但是不同宽度控制单元的最优长宽比略有差异，当Lx=3.4r时，最优长宽比Ly/Lx为0.82左右，而当Lx分别为3r、4r、5r时，这一最优值分别为0.9、0.8、0.7左右。即Ly分别为2.7r、3.2r和3.5r,且在最优长宽比下，Lx=3.4r时量纲一平均油膜压力最大。

考虑凹坑织构深度和润滑油速度对这一最优值的影响，得到不同凹坑深度下油膜压力曲线和不同速度下油膜压力曲线如图3(c)、(d)所示。可以看出，在不同的织构深度和润滑油速度下，织构单元的最优长宽比都为0.82左右，凹坑深度和润滑油速度对最优长宽比没有影响。

源于上述结果，采用基于N-S方程的CFD方法，利用Fluent软件仿真控制区域的流体迹线，如图4所示。选取凹坑半径为r=115 μm，凹坑深度h0=5 μm，最小间隙hp=5 μm，选择控制单元边长分别为3r、3.4r、4r、5r，研究凹坑分布间距对油膜承载力的影响机制。设置织构模型的上下表面为壁面边界条件，其中上表面以速度U运动，织构模型的侧面为周期边界条件，材料设置为润滑液，其中动力黏度为0.013 2 Pa·s,密度为840 kg/m3。

图4 控制区域的流体迹线

从图4中可以观察到，由于凹坑的泵吸作用[21]，流体流经凹坑时，非凹坑区域的润滑油会向凹坑区域流动，由此影响凹坑流体动压润滑的产生。结合图5中不同控制单元下凹坑长宽方向影响范围对比可以看出，随着控制单元的增大，凹坑对控制区域的影响，反映在润滑油流动的垂直方向Ly上，出现逐渐增大的趋势，当控制单元L分别为3r、3.4r、4r、5r时，凹坑对流体的影响范围在Ly方向上Ly1大约为2.67r、2.78r、3.23r、3.55r；反观影响区域的长宽比Ly1/Lx却呈现逐渐减小的趋势，即影响区域占控制区域的面积率在逐渐减小，凹坑流体影响区域长宽比分别为0.89、0.82、0.81、0.71。

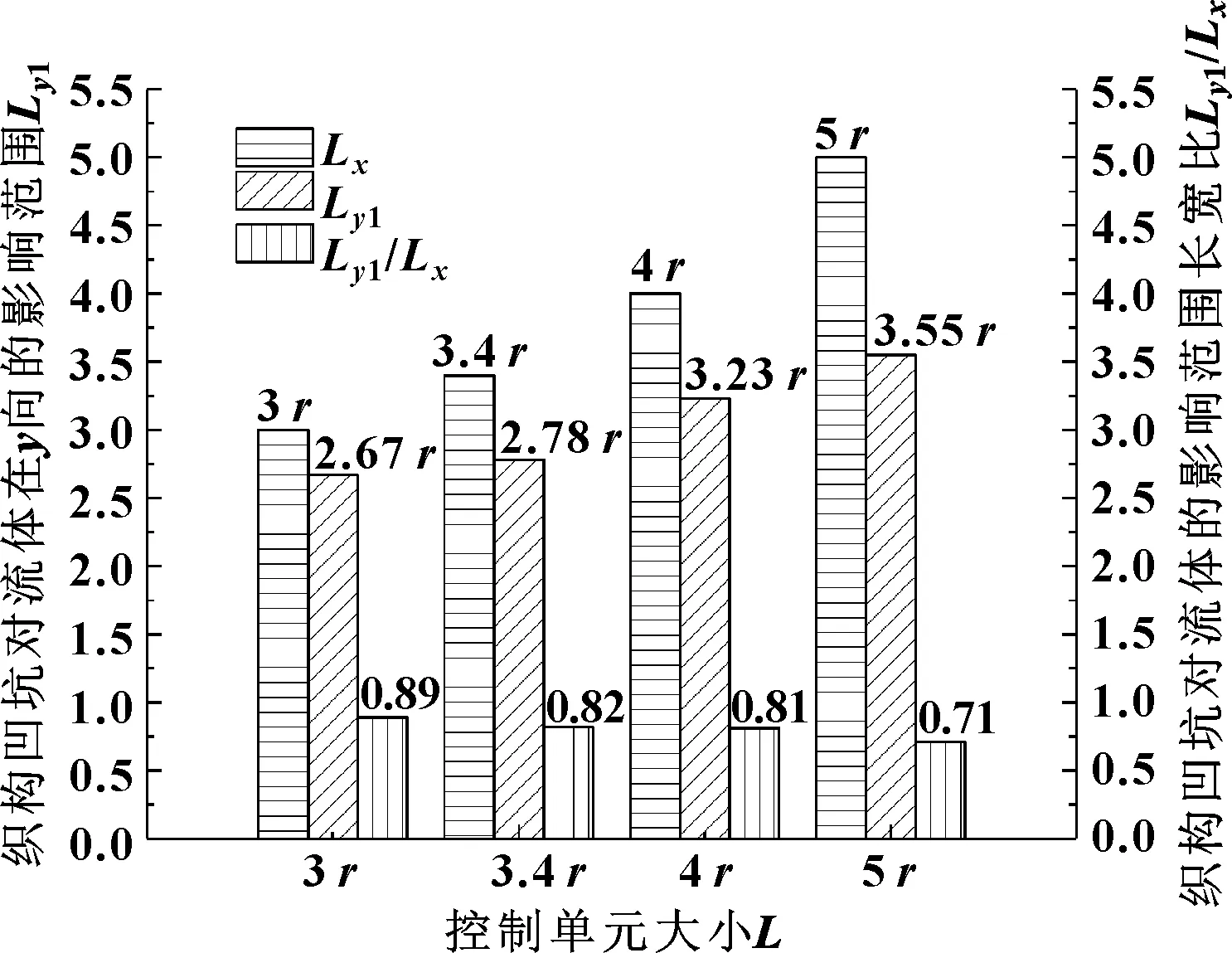
图5 不同控制单元下凹坑长宽方向影响范围对比

再分析凹坑分布间距对油膜承载力的影响机制。如图4(a)所示L=3r时，泵吸作用导致非凹坑区域的润滑油会向凹坑区域流动，影响了控制区域平均油膜压力；当控制单元逐渐增大到L=3.4r时如图4(b)所示，这一效果继续增强，凹坑对周围润滑油的影响范围持续增大，所以产生的平均油膜压力也有所增加;当控制单元继续增大到L=4r、5r时，如图4(c)、(d)所示，凹坑区域对非凹坑区域流体的影响范围虽继续增大，但此时影响区域占控制区域面积率的逐渐减小成为影响控制区域平均油膜压力的主要因素，影响区域占比的持续下降，使得泵吸作用产生的额外动压力被不能产生动压的非凹坑区域所平衡，导致了整体控制区域平均油膜压力出现下降的趋势。

同时，流体迹线图4也验证了图3的结果，当L分别为3r、3.4r、4r、5r时，凹坑影响范围的长宽比分别为0.89、0.82、0.81、0.71。这一结果和控制区域长宽比对量纲一平均油膜压力的影响结果基本吻合，故当摩擦副相对运动时，凹坑对流体的影响范围和流体的流动状态是影响控制区域平均油膜压力的主要因素之一。

为了进一步验证凹坑横纵向分布间距不等时能够获得更大的油膜承载力，选择5×5的织构模型来计算量纲一平均油膜压力，织构表面产生的油膜压力分布如图6所示。此处分别选取凹坑横向分布间距即控制单元宽边Lx分别为3r、3.4r、4r、5r,对比横纵向分布间距相等(Lx=Ly)和横纵向分布间距不等(Ly/Lx分别为0.9、0.82、0.8、0.7)时所产生的量纲一平均油膜压力的大小，如图7所示。可以看出，当适当调整Ly使凹坑横纵向分布间距不等时，可以获得更大的油膜承载力。图7中4种情况下，控制区域油膜承载力均有所提高，并且Lx=3.4r,Ly/Lx=0.82时量纲一平均油膜压力最大。所以可以得出结论：当织构单元Lx=3.4r，长宽比Ly/Lx为0.82时，即设置凹坑的横向分布间距为3.4r，纵向分布间距为2.8r,可以获得最优的油膜承载力。

图6 5×5的织构模型的油膜压力分布

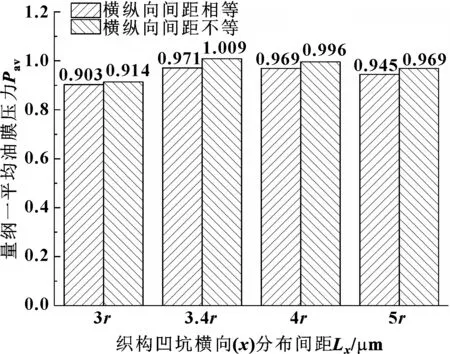
图7 2种分布间距下的油膜压力对比

3.2 协同作用下凹坑分布对油膜压力稳定性的影响

当研究单凹坑表面织构时，只需研究凹坑的几何参数对控制区域油膜承载力和摩擦力的影响进行研究，而研究多凹坑分布的织构模型时，由于织构入口的压力会受到前一个织构出口压力的影响，所以织构的压力峰值和出口压力也会随之变化，进而影响下一个织构的油膜压力。影响油膜压力波动的主要因素为凹坑分布的间距和分布形式。

以油膜压力峰值Pmax作为评价指标，研究织构模型为5×5时润滑油速度方向上油膜压力的波动情况。其中，凹坑半径r取115 μm，凹坑深度hp取5 μm，最小间隙h0取5 μm，取凹坑控制单元Lx为3.4r,Ly为2.8r,长宽比Ly/Lx为0.82。由于垂直于速度方向上的油膜压力对称，所以取计算域中心线上5个凹坑产生的油膜压力进行分析，分别得到如图8所示中心线五凹坑量纲一油膜压力分布。可以看出，油膜压力峰值的变化主要发生在边界单元处，这是由于织构间的相互影响，织构对控制区域油膜压力的影响范围会扩展到下一个织构的控制区域。这样的影响在润滑油速度方向累积，导致织构边界处凹坑影响区域受到抑制；这样的油膜压力波动会使整体控制区域对摩擦表面产生一个倾覆力，导致高精度摩擦表面产生振动，甚至运动失稳。

图8 中心线五凹坑量纲一油膜压力分布(Lx=3.4r,Ly=2.8r,Ly/Lx=0.82)

由于织构边界处凹坑影响区域受到抑制，油膜压力峰值波动主要发生在边界单元处，因此，通过适当增大控制区域边界处凹坑单元宽度来减小油膜压力峰值变化程度。在此增加边界处凹坑单元沿油膜速度方向的长度Lx,补偿边界处凹坑影响区域的减小，分别取凹坑在边界控制单元Lx为4r和5r，选择中心布置和偏置布置，织构模型如图9(b)、(c)所示。

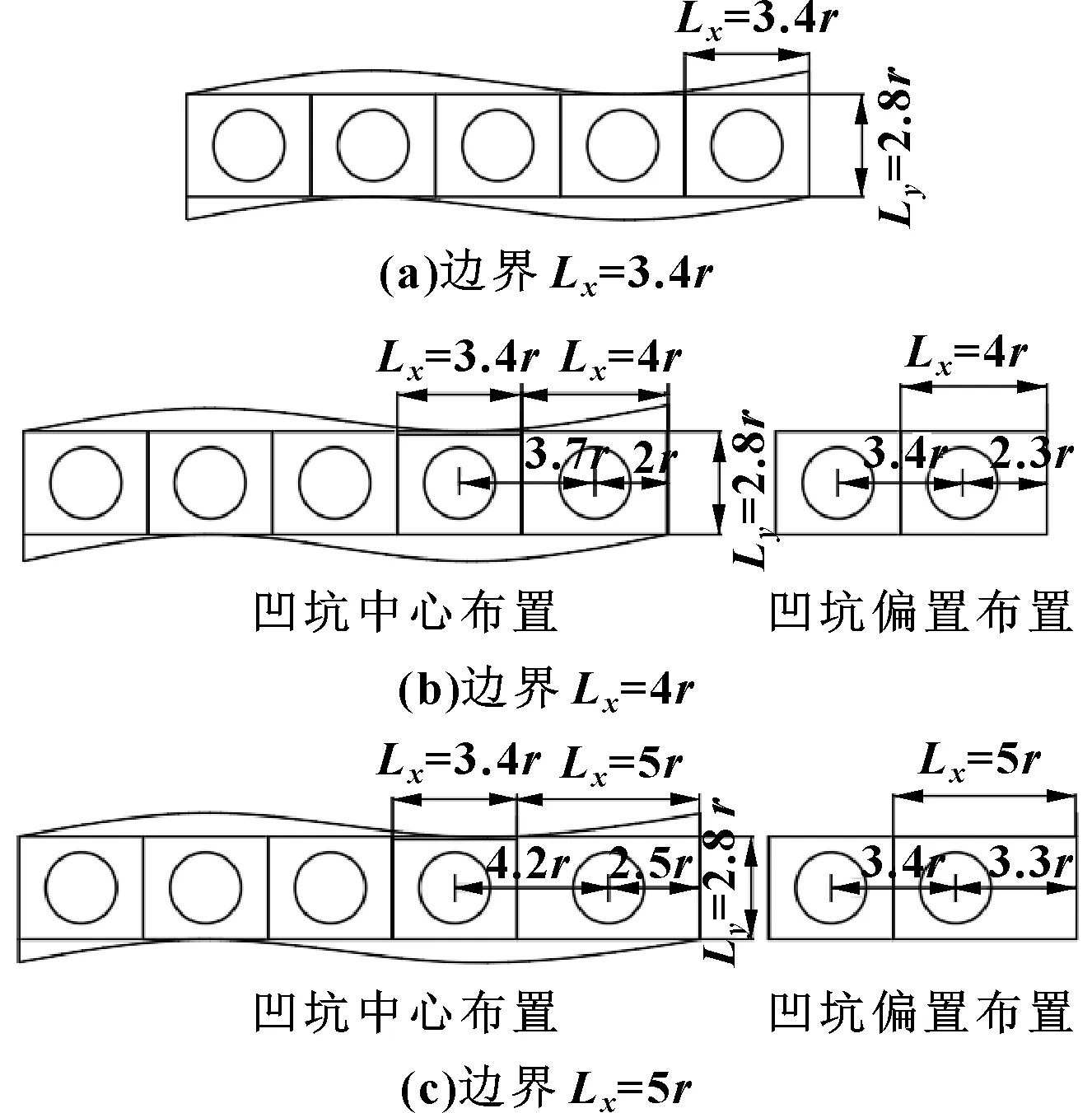
图9 边界处织构模型

计算得到计算域中心线上5个凹坑产生的最大油膜压力，如图10所示。可以看出，当边界处凹坑控制单元无偏置时，油膜压力峰值变化量明显减小，但是左侧凹坑油膜压力峰值却受边界凹坑控制单元的影响而增大；而当凹坑在控制单元内偏置布置，即适当减小与左侧凹坑的间距时，这一负面影响明显减弱；并且可以看出相比于Lx=4r,Lx=5r产生的油膜压力分布效果更好。此时，计算域中心线上5个凹坑产生的最大油膜压力基本趋于一致，有效地减小了油膜压力峰值的波动。

图10 中心线五凹坑油膜压力峰值对比

4 结论

针对球冠状凹坑织构，分别选择量纲一平均油膜压力和油膜压力峰值作为动压润滑性能的评价指标，研究了表面织构分布间距对油膜压力数值大小和油膜压力稳定性的影响，并研究表面织构分布间距对油膜压力的影响机制。总结研究结果可以得到以下结论：

(1)控制区域量纲一平均油膜压力随凹坑控制单元边长的增大，先逐渐增大再缓慢减小。当控制单元边长L=3.4r，即凹坑分布间距为3.4r时，油膜压力达到最大值。

(2)考虑控制单元长宽不等的情况，即凹坑横纵向分布间距不等对平均油膜压力的影响。当Lx为3.4r恒定时，随凹坑控制单元边长Ly的增大，控制区域平均油膜压力同样先逐渐增大再缓慢减小，当织构单元Lx=3.4r，Ly=2.8r，长宽比Ly/Lx为0.82时，即设置凹坑的横向分布间距为3.4r，纵向分布间距为2.8r，可以获得最优的油膜承载力。与横向和纵向间距相等的凹坑分布相比，当凹坑横纵向分布间距不等时，油膜压力得到了进一步提高。

(3)当织构模型为多凹坑分布时，由于凹坑之间的协同效应，会使得凹坑之间的油膜压力峰值产生波动，尤其是边界凹坑油膜压力骤减，当增大边界凹坑的控制单元Lx=5r，并且将凹坑中心适当偏置，使边界凹坑两侧间距基本相等都为3.4r左右时，可以有效地提升边界处凹坑的油膜压力使油膜压力更加稳定。

(4)泵吸作用导致非凹坑区域的润滑油向凹坑区域流动，影响了控制区域平均油膜压力。当控制单元逐渐增大时，凹坑对周围润滑油的影响范围增大，所以产生的平均油膜压力也有所增加。当控制单元继续增大时，凹坑区域对周围区域流体的影响范围虽继续增大，但此时影响区域占控制区域比率却逐渐减小，使得泵吸作用产生的额外动压力被不能产生动压的非凹坑区域所平衡，导致了整体控制区域平均油膜压力出现下降的趋势。这也是油膜压力会随凹坑控制单元边长的增大先逐渐增大再缓慢减小，存在最优值的原因。