硅漂移探测器时间分辨优化仿真研究

虞 年 徐玉朋 蔡严克 祝宇轩 赵晓帆 陈 灿

1（中国科学院高能物理研究所 北京 100049）

2（中国科学院大学 北京 100049）

3（吉林大学物理学院 长春 130012）

硅漂移探测器近年来在空间探测中得到广泛应用，例如风云二号F 星［1］、火星科学实验室［2］（Mars Science Lab，MSL）和中子星内部组分探索者［3］（Neutron Star Interior Composition Explorer，NICER）都搭载了SDD。早期SDD 主要用于探测入射粒子的位置信息［4］，之后又因其突出的能谱性能而被广泛用于X射线荧光分析领域［5］。典型SDD的结构如图1所示，整体采用圆柱形结构，上表面分布着一系列p+型同心环状电极，在第一环和最后一环电极上加偏置电压，通过片上集成的分压电路在这些同心环上形成梯度电压，使得探测器内部产生漂移电场。上表面中心是读出阳极，点状阳极使得探测器电容很小并且独立于探测器灵敏区面积，因此适用于高计数率、高能量分辨的能谱测量场合［6］。

入射粒子与SDD 灵敏区发生相互作用之后产生电荷包，在漂移电场的作用下，电荷包向阳极漂移并被收集形成输出信号。由于环状电极的屏蔽作用，电荷包在漂移过程中不会在阳极上感应出电荷直至越过第一环电极，因此电荷包从产生位置到阳极附近存在一段漂移时间，漂移时间会随着入射位置变化而改变，一般在μs·cm−1量级［7］，通常不能直接测量，其不确定性是影响SDD系统时间分辨的主要因素，并且随着探测器面积增大时间分辨会显著恶化。

图1 典型硅漂移探测器结构[6]Fig.1 Schematic diagram of a typical silicon drift detector[6]

1 时间分辨优化方法

电荷包在向阳极漂移过程中会发生热扩散［8］。在能量沉积、工作温度和外置偏压保持不变的情况下，电荷包产生位置离阳极越远，到达阳极时的体积越大，阳极收集电荷时间越长，电荷灵敏放大器（Charge Sensitive Amplifier，CSA）输出信号的上升时间也越长（如图2 所示）。文献［9］给出的测试结果显示上升时间和漂移时间之间存在明显的对应关系，理论上可以通过直接测量上升时间得到电荷包的漂移时间。但是CSA 输出信号上升时间较短且信噪比较差，直接采样对模拟数字转换器（Analog to Digital Converter，ADC）性能要求非常高。另外信号噪声大，上升时间测量误差也大，因此很难在实际测量中使用。

图2 电荷灵敏放大器对不同输入脉宽电流脉冲的响应Fig.2 Response of the CSA with respect to current pulses with different pulse width

CSA输出信号可以采用成形网络进行滤波处理来提高信噪比。相同电荷量、不同上升时间的信号经过成形网络后的幅值不同，上升时间越长，成形脉冲幅度损失越大，这就是弹道亏损效应，另外不同成形网络对输入信号上升时间的敏感程度也不同［10-11］。如果能找到两种成形网络，其中一种对输入信号上升时间敏感，将其称之为弹道亏损成形网络（Ballistic Deficit Shaping，BDS）；另一种对上升时间不敏感，称为弹道亏损免疫成形网络（Ballistic Deficit Immunity Shaping，BDIS）。将两种网络对同一输入信号的脉冲幅度比R定义为：

R将只依赖于输入信号的上升时间，而与输入信号的幅值无关。选择合适的成形网络和时间参数，通过幅度比可以显著提高漂移时间的“测量”精度，使修正后的粒子到达时间分辨性能更好。

2 成形网络选择

成形网络的选择通常需要在最佳信噪比、弹道亏损效应之间进行折中。文献［11］指出在常用的成形电路中，三角成形对CSA输出信号拥有最好的滤波性能，并且对输入信号的上升时间非常敏感，因此本文选用三角成形当作BDS 网络。若将三角成形的尖顶做平台化处理后可以得到梯形成形，通过设置合适的参数，使梯形成形的平顶时间大于输入信号的上升时间，就可以使得梯形成形对输入信号上升时间免疫，而且依然拥有良好的滤波性能，因此可选用梯形成形作为BDIS网络。如图3所示，本文定义从波形起始时刻到峰值时刻的时间为达峰时间tp，梯形顶部的平顶时间为tft，三角成形和梯形成形的脉冲宽度分为2tp和2tp+tft。图3 中三角成形和梯形成形的达峰时间一致，但考虑到成形时间越短，脉冲幅度损失越明显，因此本文设置三角成形的达峰时间小于梯形成形。三角和梯形成形算法具有处理过程简单，成形速度快，成形后脉冲宽度窄，成形参数可调，线性良好等特点，满足脉冲堆积概率低、基线偏移小、噪声抑制强等特点［12］，并且数字化算法易于在现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）中实现。

图3 成形网络参数定义Fig.3 Parameters definition of shaping network

3 信号链建模仿真

SDD 读出信号链的基本组成包括：CSA、RC 微分器、ADC波形采样模块、FPGA数字滤波模块和数据获取储存单元。由于SDD存在暗电流，CSA输出的波形是一个个小的准阶跃脉冲信号（有效信号）叠加在缓慢增长的斜坡信号（暗电流信号）之上。由于有效信号的幅度值比斜坡信号小两个数量级左右，考虑ADC 采样精度，一般先将CSA 输出信号经过RC 微分电路，滤除掉暗电流成分，同时将有效信号整形为指数衰减波形。然后将指数衰减信号进行适当放大后送给ADC 进行波形全采样，再送入FPGA进行数字滤波处理。三角和梯形成形的传递函数为［13］：

式中：τ为RC微分电路的时间常数；Ts为采样周期；na=tp/Ts；nb=（tp+tft）/Ts。

得到传递函数之后就可以利用软件进行仿真，考虑在数字化处理中截断、舍入的影响以及后续硬件描述语言的转换，本文采用Matlab/Simulink 中自带模块和System Generator 中Xilinx 模块搭建系统进行联合仿真。

3.1 脉冲产生模块

利用一个矩形脉冲产生器和一个积分器就可以模拟SDD和CSA系统，矩形脉冲经过积分之后就会产生一个上升时间正比于脉冲宽度的准阶跃信号，改变矩形脉冲的宽度可得到不同的上升时间，以此来模拟探测器漂移时间的影响。再用零极点模块模拟RC微分器，产生指数衰减信号，该模块的输出波形如图4所示。

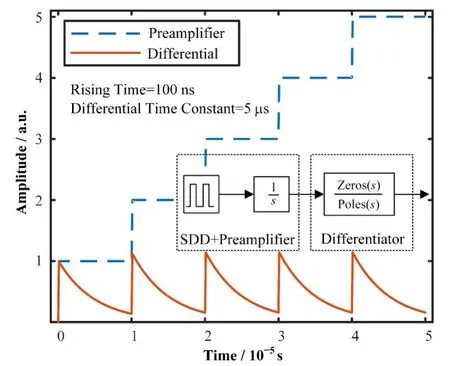
图4 脉冲产生模块的组成和输出波形Fig.4 Composition of the pulse generation module and output waveforms

3.2 ADC模块

ADC 的分辨率和采样率是影响采样精度的主要因素。核脉冲信号前沿非常陡峭又具有随机性，因而ADC 不能保证恰好采集到信号峰值。如图5所示，VSa是ADC 采集到的最大值，Vmax是指数信号的最大值，ΔVmax是VSa和Vmax差值的最大值，其表达式为式中：τ是微分器时间常数；fSa是ADC 采样频率。由此可知采样率越高，峰值采样误差越小。假设由ADC 分辨率和采样率贡献的噪声均方根（Root Mean Square，RMS）分别σN和σSa，则总噪声本文对σADC进行了数值计算，结果如图6 所示，其中纵坐标为σADC与入射粒子能量E的比值，横坐标为ADC 的采样率，不同曲线代表不同的分辨率，ADC 能量测量范围为0～15 keV。图6 中横向虚线代表SDD 和低噪声CSA总读出噪声值，其等效噪声电荷RMS可以做到 5 个电子［14］，ADC 贡献的噪声需要低于此噪声线。

图5 波形采样示意图Fig.5 Schematic diagram of waveform sampling

图6 理想ADC总噪声随采样率和分辨率的变化Fig.6 Total noise of an ideal ADC varies with the sampling rate and resolution

利用Simulink自带的模块对ADC进行建模，该模块主要包括零阶保持器、理想ADC 量化器、移位算法器和数据类型转换器。零阶保持器在时钟上升沿对输入信号进行全精度采样并保持到下一个时钟上升沿，其采样频率设置为50 MHz。理想ADC 量化器将存储在零阶保持器中的全精度值转换为最接近的量化数，量化器的精度设置为12 bit。移位算法器和数据类型转换器将量化器输出的二进制整数转换为符合要求的定点数。

3.3 成形模块

从三角成形和梯形成形的传递函数可知，该系统为无限冲击响应系统，为了避免截断和舍入误差的积累，故选用级联结构来实现：

式（4）是梯形成形传递函数的级联形式，三角成形级联结构与之类似。梯形成形系统的级联结构图如图7 所示。H1(z)是将输入延迟一个时钟周期后与常数做乘法运算，再和原输入做差，这相当于把叠加的指数衰减信号整形成为一个个冲击脉冲，达到去除尾部的目的。H2(z)与H3(z)结构类似，可看成先对输入做累加运算，然后将累加结果延迟na或nb个时钟周期，再将延迟结果与累加结果做差，冲击脉冲通过H2(z)和H3(z)处理之后就产生了梯形轮廓。H4(z)是将输入延迟一个时钟周期后与常数1/na做乘法运算，经过H4(z)处理之后就形成了上升、下降沿完全对称的等腰梯形结构。

图7 梯形成形算法的级联结构图Fig.7 Block diagram of the trapezoidal shaping algorithm

4 结果分析

4.1 脉冲幅度比仿真

上文阐述了漂移时间测量的原理，其中关键的是要求成形网络的脉冲幅度比只与输入信号的上升时间tr有关，而与输入信号的幅度无关。为了检验三角成形和梯形成形的脉冲幅度比是否符合上述要求，做了如下仿真：设置梯形成形的达峰时间tp=2 μs，平顶时间tft=0.2 μs，三角成形的达峰时间tp=0.2 μs，ADC 模块的采样率为 50 MHz，分辨率为12 bit，RC微分器的时间常数为5 μs。在此条件下分别选取了 3 个典型的上升时间：10 ns、50 ns 和100 ns。在不同上升时间下改变输入信号的幅值，0.1～1 V，步长为0.1 V。仿真结果如表1 所示，由于ADC 位数有限，仿真得到的幅度值存在量化误差，因此表中不同上升时间下的R值略有波动，其相对误差最大值为5.7×10−4。在误差允许范围内，可认为R值只与上升时间有关，与输入幅度无关，这与预期相符合。

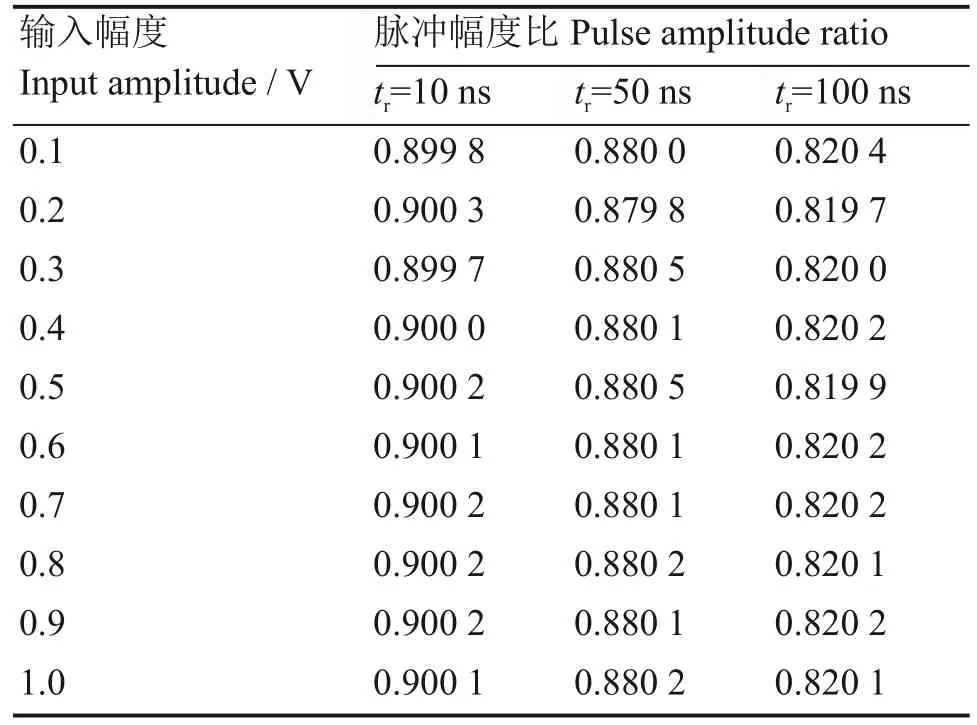
表1 不同上升时间下脉冲幅度比与输入幅度的关系Table 1 Relationship between pulse amplitude ratio and input signal amplitude at different rising time

4.2 脉冲幅度比误差分析

根据式（1）可得到脉冲幅度比标准误差σR的表达式：

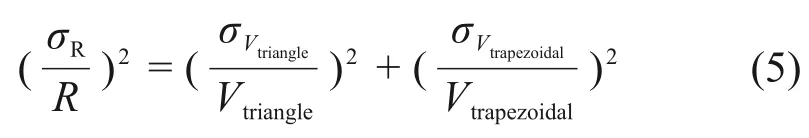
式中：Vtriangle、σVtriangle和Vtrapezoidal、σVtrapezoidal分别是三角脉冲和梯形脉冲的幅值和标准误差。

由式（5）可知σR主要决定于成形网络输出信噪比，其中噪声主要来源于SDD和CSA组成的前级系统。对于同一成形网络，入射粒子的能量越高，R的测量误差越小。对于相同能量的入射粒子，成形网络的滤波效果越好，R的测量误差越小。成形网络的滤波效果主要取决于它的成形时间，通常需要在实测中优化成形时间。对于SDD前级系统，后端成形网络的成形时间一般为几微秒。本文将梯形成形的达峰时间选为2 μs。三角成形的达峰时间越短，脉冲幅度损失越明显，但是较短的达峰时间会使噪声变大，影响脉冲幅度比测量精度，综上考虑将其达峰时间选为0.2 μs。

为了评估此参数下三角成形和梯形成形的滤波效果，进行了如下仿真：在脉冲产生模块中加入白噪声，输入信号幅值为0.8 V，噪声RMS 为0.01 V。仿真了10万个脉冲，输入输出波形如图8所示，图8中指数衰减波形是加入白噪声后的输入信号。统计得到三角脉冲幅度均值为0.717 2 V，标准差为4.25×10−3V，梯形脉冲幅度均值为0.796 7 V，标准差为1.45×10−3V。可见信号经过成形网络后信噪比得到了大幅改善。

图8 加入白噪声后的负指数输入波形和成形网络输出波形Fig.8 Input exponential decay waveform with white noise and output waveform of shaping networks

4.3 漂移时间修正及其误差估算

漂移时间和上升时间之间的关系与SDD 制造工艺、偏置电压、工作温度和CSA带宽等有关，因而对于一款特定的SDD 和CSA，其漂移时间td和上升时间tr需要通过实测来确定。本文利用文献［9］测试得到的td和tr的数据点进行拟合，拟合结果如图9（a）所示，得到漂移时间误差σtd与上升时间误差σtr的关系。然后仿真得到脉冲幅度比R和tr之间的关系并对这些数据点进行拟合，拟合结果如图9（b）所示，得到σtr和脉冲幅度比误差σR之间的关系。再对σR进行估算：对于现在商用的SDD，在达峰时间为0.2 μs 的情况下，等效噪声能量RMS 约 25 eV［15-16］。为了保守估算，本文设定三角成形输出噪声RMS为50 eV，则梯形成形输出噪声RMS约为15 eV。设置上升时间tr=50 ns，入射粒子能量E=5.9 keV，根据式（5）可以计算得到σR=7.79×10−3，最后根据误差传递关系得到σtd=26 ns。根据文献［9］中SDD 漂移时间和入射光子位置的关系，假设光子均匀入射到半径为2 mm 的SDD 上，由入射位置不确定性造成漂移时间的均方根约为240 ns。对比二者可以发现，通过脉冲幅度比得到漂移时间可以很好地提升SDD的时间分辨性能。

图9 文献[9]测试得到的漂移时间和上升时间的关系(a)，仿真得到的上升时间和脉冲幅度比的关系(b)Fig.9 Relationship between drift time and rising time in Ref.[9](a),and relationship between rising time and pulse amplitude ratio obtained by simulation(b)

5 结语

SDD 中电荷包的漂移时间随着粒子入射位置改变而发生变化，漂移时间的不确定性是影响SDD系统时间分辨的主要因素。本文利用三角成形和梯形成形信号的脉冲幅度比来确定电荷包的漂移时间。SDD 和CSA 组成的前级系统的电子学噪声是脉冲幅度比测量误差的主要来源，提高成形网络的信噪比可以提高脉冲幅度比的测量精度，从而减少漂移时间测量误差。仿真得到漂移时间误差的典型值为σtd=26 ns @tr=50 ns，这将SDD 时间分辨提高了一个数量级。后续将完成脉冲幅度比方案的硬件设计和测试工作，得到SDD系统的时间分辨性能。