虚拟单点源构建医用直线加速器束流模型的探讨

李惠娟 焦胜修 陈仲本 刘小伟

1（中山大学新华学院 广州 510520）

2（中山大学物理学院 广州 510275）

放射治疗是癌症治疗的三大主要手段之一。医用直线加速器是目前放射治疗的主流设备，其基本原理是通过高能电子打靶产生X射线对病灶区进行照射，从而达到抑制和控制肿瘤的目的。为了达到该目的，吸收剂量计算是放射治疗计划制定的出发点，而医用直线加速器的束流模型是完成剂量计算所必须的基础之一。因此对医用直线加速器束流模型的研究在放射剂量计算的临床应用具有重要的意义。

医用直线加速器X射线的束流描述主要是蒙特卡罗模拟得到的相空间集合或由此得到的特性［1−2］和基于测量的剂量分布进行参数拟合的虚源模型［3−8］。采用蒙特卡罗方法，根据实际加速器的结构，可模拟得到机头出射粒子的相空间集合。虽然利用出射粒子的相空间集合更准确地描述了加速器的束流，但由于各加速器之间存在差异，需针对具体的加速器进行模拟，这需要厂家提供具体的加速器机头的几何及材料参数进行模拟。虚源模型是采用虚拟的多个源对机头出射的粒子进行描述，各源的权重通过对实测的剂量分布（如百分深度剂量（Percentage Depth Dose，PDD）、离轴剂量比（Off Axis dose Ratio，OAR）、总散射因子（SCP）等），进行拟合得到。医用加速器的X射线可分为原射线和散射线，散射线主要来源于均整器，在虚源模型中多用面源进行描述。但面源在束流方向及强度处理上较点源复杂，而采用点源将大大简化吸收剂量的计算。由于点源在射野中心点产生的注量不随射野尺寸而变化，因而其不能正确描述散射源。采用高斯函数进行卷积可使点源在射野中心点产生的注量随射野尺寸而变化，从而得到面源的特征［9］。而本文尝试采用另一种更简单的方法，通过设置点源的强度与射野的面积相关来描述散射源。

本文初步探讨了一种源强与射野的面积相关的单点源来描述散射线的医用直线加速器X射线束流的虚源模型，并通对过实际测量的剂量分布进行参数拟合来检验模型的适用性。

1 材料与方法

1.1 加速器X射线的单点源束流模型

加速器的结构示意图如图1 所示，其主要部件有 X 射 线 靶（Target）、初 级 准 直 器（Primary Collimator）、均整器（Flatting Filter）、监测电离室（Monitor Chamber）、反射镜（Mirror）、次级准直器（Secondary Collimator）及射野挡块（Jaws）、多叶准直器（Multi-leaf Collimator，MLC）等。均整器的作用是对X 射线束进行调制。经过均整器调制后，靠近中心轴的光子数减少，这样就使得整体的光子注量分布沿半径方向上较为平坦，从而使得它在模体中产生的剂量分布变得平坦。

图1 医用直线加速器模型示意图Fig.1 Sketch map of linear accelerator model

单点源束流建模中，点源坐标原点设在靶的中心点，Z轴的方向为图1 中箭头的指向。注量由式（1）描述：

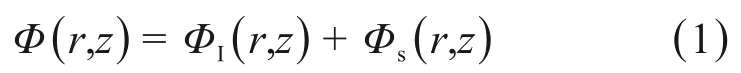
式中：Φ(r，z)为位置(x，y，z)处的注量，r2=x2+y2；ΦI(r，z)为打靶处产生射线贡献份额，本文中称为原射线；Φs(r，z)为均整器以及准直器等部件产生散射线，该部分与射野有关的注量分布，本文称为散射线。

1.1.1 原射线建模

由于电子打靶产生的韧致辐射光子发射不是各向同性的，同时考虑到均整器的调制作用，将原射线建模为各向异性的点源，射野内射线的注量分布由式（2）描述：

式中：Φ0可看成一种归一化常数；ɑ1、ɑ2、ɑ3为待拟合的参数。

1.1.2 散射线建模

散射线建模为强度与射野有关的点源。射野内的散射线注量分布由式（3）描述：

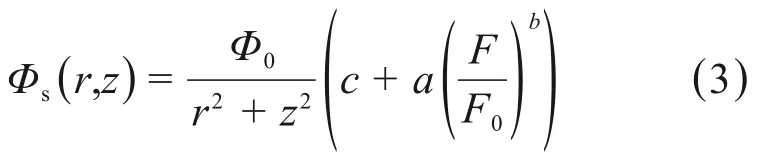
式中：F代表射野的面积；F0为参考射野的面积，实际处理时采用边长10 cm的方野的面积。

1.1.3 射野外的注量

由于本文主要关注射野内的剂量，对于射野外的注量，仅采用简单的指数下降函数来描述：

式中：Φout(d)代表射野外距射野边缘的距离为d处的注量；ΦB代表射野边缘处的注量；α为衰减系数，通过调整其大小来符合野外的剂量分布。

1.1.4 射线的能谱

对医用直线加速器X 射线能谱的研究，主要采用蒙特卡罗方法［2，10−11］，如 Mohan 等［10］利用 EGS3 模拟计算了 Varian 不同机型的 X 射线能谱；Ding［2］利用EGS4 模拟计算了Varian2100EX 的X 射线能谱。在本研究中，剂量计算采用的X 射线能谱由BEAMnrc 对 Varian TRILOGY 模拟得到，同时在计算中不考虑原射线和散射线能谱的差异。

1.2 加速器剂量分布的测量

测量采用0.13 cm3指形电离室（IBA，德国）在三维水箱（Blue Phantom，IBA，德国）测量 Varian TRILOGY 加速器6 MV 光子线在水中的剂量分布。该系统包括水箱、控制单元、探头、储水水箱、升降台、计算机及控制软件。水箱的体积为48 cm ×48 cm × 41cm，分 辨 率 为 0.1 mm，定 位 精 度为 ±0.1 mm，定 位 重 复 性 为 ±0.1 mm。 对3cm × 3cm、10 cm × 10 cm、40 cm × 40 cm 射野，分别测量了相应的SCP、PDD 和5 cm、10 cm、20 cm 的OAR 用于模型拟合，并测量了6 cm × 6 cm、15cm ×15cm、20 cm × 20 cm 和 30 cm × 30 cm 射野的SCP对模型进行检验。测量中源皮距SSD= 100 cm，SCP测量的深度为5 cm。

1.3 模型参数的确定

对于某一个射野F，射野内的各分项注量f0=对应的 分 项 剂 量 分 布 分 别 为DF，0(r，z)、DF，1(r，z)、DF，2(r，z)和DF，3(r，z)，则在此射野下的剂量为：

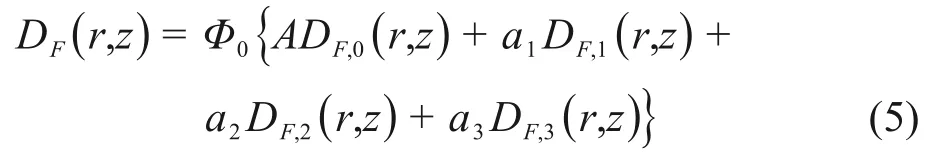
式中：第一项包括了原射线的第一项和散射线项对剂量的贡献，其中模型有意义的是ɑ1、ɑ2、ɑ3、ɑ、b和= 1+c这6个参数。

DF，0(r，z)、DF，1(r，z)、DF，2(r，z)和DF，3(r，z)可通过笔形束［12−13］、筒串卷积［14］或蒙特卡罗等方法计算得到，这里我们采用笔形束算法。

笔形束算法的积分核由式（6）描述：

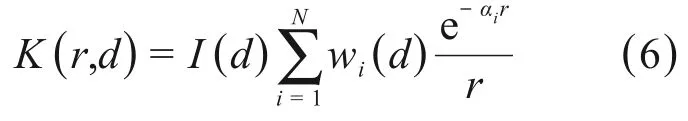
其中：I(d)为积分核的深度分量，其径向部分，除了权重因子wi(d)外，与深度d无关。分项剂量DF，k(x，y，d)可通过积分核与分项注量fk(x，y，d)的卷积得到：

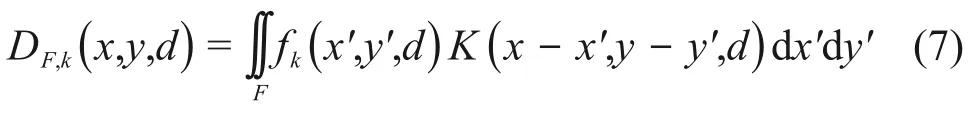
式中：fk(x'，y'，d)为深度d处对应的第k项注量，k=0，1，2，3。在实际计算时，我们采用一种发散型坐标系（Fan-line coordinate）［13］，在这种坐标系下，积分核的深度分量I(d)和不同深度的径向权重因子wi(d)是通过对EGSnrc 蒙特卡罗程序模拟得到的一系列不同半径的锥束X 射线的剂量分布对式（6）进行拟合而得到。采用发散型坐标系，注量形式上与深度d无关，因此剂量计算时不用对各个深度进行卷积运算，提高了计算效率。

束流模型的参数通过对测量的剂量分布拟合得到，即通过调整参数使得目标函数最小。目标函数T为：

式中：F代表射野为射野F下(ri，zj)处的测量剂量。当设定某一个参考剂量时，如10 cm ×10 cm射野最大剂量点处的剂量，它们可由测量得到的SCP、PDD 和OAR 确定。考虑到建成区的电子污染的影响，模型只对建成区之后的剂量进行拟合。

2 结果

表1给出了模型参数拟合的结果。从拟合结果来看，当射野从 3cm × 3cm 增加到 10 cm × 10 cm时，式（5）中A的值从 0.896 增加到 0.998，增加了12%；而从10 cm × 10 cm增加到40 cm × 40 cm时，A的值增加了8%，这表明小射野时，散射的贡献随散射面积而较快增加。

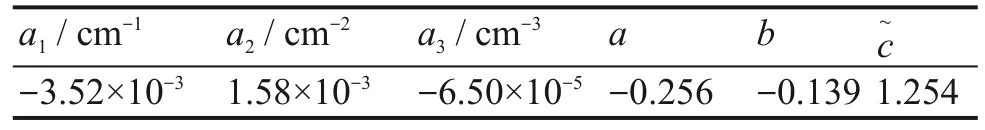
表1 模型参数的拟合结果Table 1 Fitting results of model parameters

图2给出了在不同射野下深度剂量分布的拟合值与测量值的比较。在建成区以后，拟合值与测量值在各个射野下都很好地符合。对于3cm × 3cm、10 cm × 10 cm、40 cm × 40 cm 射 野 ，从 水 下 深 度1.4 cm（最大剂量深度）到水下深度20 cm，剂量的拟合值与测量值的平均差异分别为1.3%、1.3%和1.1%；而从水下深度20 cm 后的平均差异分别为3.4%、2.0%和3.7%。水下深度20 cm后的差异较大的原因可能是拟合所用到的离轴剂量比对应的深度局限于20 cm前，没有对水下深度20 cm后的离轴剂量比进行拟合。在建成区内，拟合值与测量值差异很大，这是因为建成区内存在电子污染，而模型不考虑污染电子。

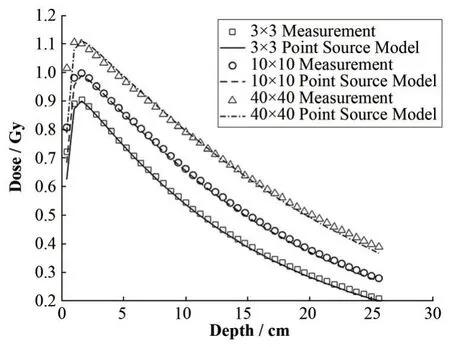
图2 不同射野下深度剂量拟合值与测量值Fig.2 Comparison between fitting values and measured values of depth dose in the different fields

图3分别给出了水下深度5 cm和10 cm处的不同射野下离轴剂量的拟合值与测量值的比较。由图3 可以看出，总体上拟合值与测量值差异不大。在5 cm 处 ，对于 3cm × 3cm、10 cm × 10 cm、40 cm ×40 cm射野，在OAR大于90%的区域，剂量的拟合值与测量值的平均差异分别为1.76%、1.30% 和0.65%；在10 cm处，分别为2.35%、0.75%和0.53%。

图3 不同射野水下5 cm(a)、10 cm(b)测量值与拟合值的离轴剂量比Fig.3 Comparison between fitting values and measured values of off-axis dose in the different fields at the depth of 5 cm(a)and 10 cm(b)underwater

图4 给出了不同射野的SCP的测量值与拟合值比较。由图4 可以看出，总体上测量值与拟合值符合很好。3cm × 3cm射野的拟合值与测量值相差了1.42%，10 cm × 10 cm射野的拟合值与测量值相等，而40 cm × 40 cm 射野的拟合值与测量值相差0.55%。 对 于 作 为 检 验 的 6 cm × 6 cm、15cm ×15cm、20 cm × 20 cm和30 cm × 30 cm射野，SCP的拟合值与测量值相差小于0.5%。

3 讨论

X射线束流模型的建立应该包含原射线和散射线。原射线通常设为点源。蒙特卡罗模拟表明散射光子最大的来源是均整器，其次是初级准直器，而来自于次级准直器（JAW、MLC）的散射光子数只占总散射光子数的0.2%［15］。因而对散射线建模时，常将其设置为面源（均整器）和环源（初级准直器），而将可运动并构成不同射野的次级准直部件（如JAWs和MLC）看成吸收体。但在计算束流注量时面源以及环源需将源划分为点源计算后累加，这相对于点源大大增加了计算的时间。考虑到次级准直部件对面源一些位置发射出光子的阻挡和吸收作用，将散射线建模为强度随射野变化的点源可能是有益思路，它不仅具有面源对射野内注量随射野面积变化的特点，同时减少剂量计算的时间。

图4 不同射野散射的总散射因子SCP的测量值与拟合值比较Fig.4 Comparison between fitted values and measured values of SCP in the different fields

本文探讨了一种简化的强度与射野的面积相关的单点源束流模型，此简化模型没有考虑原射线和散射线能谱的差异、没考虑原射线和散射线的点源位置的差异，对于射野外的注量，仅采用简单的指数下降函数来描述。尽管模型简单，但它却很好地描述了射野内的剂量分布，准确地给出了SCP随射野变化的关系，这说明采用与射野面积相关的点源来描述散射线是可行的。

4 结语

本文初步探讨了一个非常简单的单点源医用加速器的X射线束流模型。该方法只是对采用单点源的模型初步探讨，进一步可以考虑原射线以及散射线的能谱差异，从而可进一步提高模型的准确度。而散射线的能谱，可通过蒙特卡罗模拟等方法来得到。在此模型中，单点源注量随射野变化。结果表明：此射线束流模型可很好地重建体膜内的三维剂量分布，给出正确的总散射因子。