从“猫抓老鼠”谈利用中点解决线段最值问题

广东省广州市南沙区教育发展中心(511458) 黄安锦

《数学课程标准(2011 版)》强调学生亲历知识的发展过程,能将现实问题抽象并转化为数学问题,并体会其中的数学思想方法,在获得四基的同时,四能得到培养,最终发展成终身学习所需的数学学科核心素养.最值问题是学生初中阶段必须掌握的重要内容,也是近年各地中考的热点,此类问题一般具有涉及知识面广、命题类型多、生活应用性强等特征,对学生的综合解题能力要求也较高.部编版八年级上册“13.4 课题学习——最短路径问题”重点描述了将军饮马和造桥选址两类问题,这是最常见的线段最值问题,主要依据是“两点之间线段最短”.深入探究后我们发现,“线外一点到线上动点最短距离为垂线段距离”,“点心所在直线上可以找到点和圆上的点间最长距离或最短距离”也是解决线段最值问题的常用方法.在刚结束广东省2020 年中考中也出现了一道以“猫抓老鼠”为问题背景的线段最值问题,本文以该题的解题模型分析为契点,谈谈线段最值问题的解题策略.

1 题目再现

有一架竖直靠在直角墙面的梯子正在下滑, 一只猫紧紧盯住位于梯子正中间的老鼠, 等待与老鼠距离最小时扑捉.把墙面、梯子、猫、老鼠都理想化为同一平面内的线或点,如下图1,∠ABC= 90°,点M、N分别在射线BA、BC上,MN长度始终不变,MN= 4,E为MN的中点, 点D到BA、BC的距离分别为4 和2.在此滑动过程中,猫与老鼠的距离DE的最小值为____.

试题分析: 本题涉及直角三角形的基本性质、线段的最短距离,对学生的数学模型思想进行了考查.此题看起来就是求两点之间的最短距离,很多学生看到题目的同时“两点之间,线段最短”的结论就出来了,但在对试题进行深入了解后深叹解决问题的方法没想象中那般简单,老鼠所在的E点是MN上的一个动点,而试题中并未直接给出E点的运动轨迹,E点随着梯子MN的滑动而发生改变,与常见的“将军饮马”中的在定直线上找动点的方向大相径庭,无法找到解题的关键突破后导致失分.

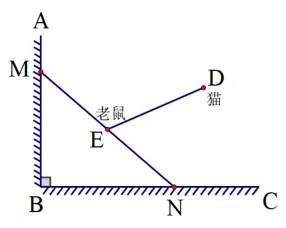
图1

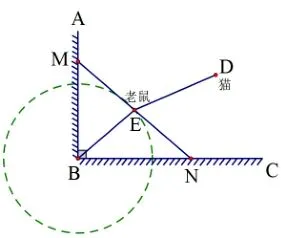
图2

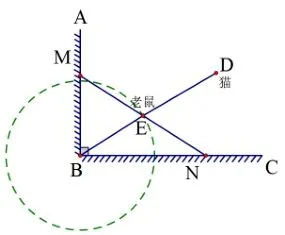
图3

解题分析: 本题的解题关键在于如何确定点E的运动轨迹,题目中给出了几个非常重要的信息: ①ΔABC是直角三角形; ②点E是斜边MN上的中点; ③MN= 4,斜边长度为定值.我们不难发现,BE为RtΔMBN斜边MN上的中线,则BE=点B与点E间的距离为定值,随着MN的移动,点E的运动轨迹为圆弧(如上图2).猫与老鼠的距离为点D到⊙B上点E的距离,利用“点到圆的位置关系”可以判断,当BD交⊙B于点E时,DE取得最小值(如上图3),答案也油然于纸上,DE=

2 利用中点解决线段最值问题策略

常见的几何图形通常会作为线段最值问题的常见载体,而其中涉及线段中点的线段最值问题也是各地命题中的“香饽饽”,这类问题的解题关键往往与三角形的中线或者中位线相关,如何找出动点的运动轨迹从而构建出解决问题的数学模型则为解决这类问题的难点.像前面中考题中出现的动点是定长动线段的重点, 且该线段为某直角三角形的斜边,这类问题只要紧紧抓住“直角三角形斜边上的中线等于斜边的一半”这一基本性质,基本可以确定该点的运动轨迹为以直角顶点为圆心,以中线长为半径的圆或某段圆弧上,在点到圆的位置关系及三角形三边的关系往往能轻松破解这类线段最值问题,如2020 年广东省中考中出现的“猫抓老鼠”问题就属此类,下面通过几类变式练习对解决以三角形为载体的线段最值问题的策略进行探索.

变式1如图4,在坐标系xOy中,点A和点B分别为x轴正半轴和y轴正半轴上的点,且AB=4,点C为线段AB的中点,点D为(3,4).当OC+CD最小时,求此时点C的坐标.

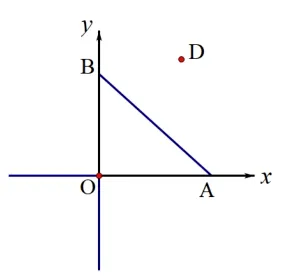
图4

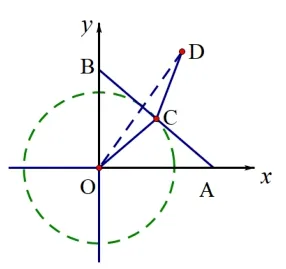
图5

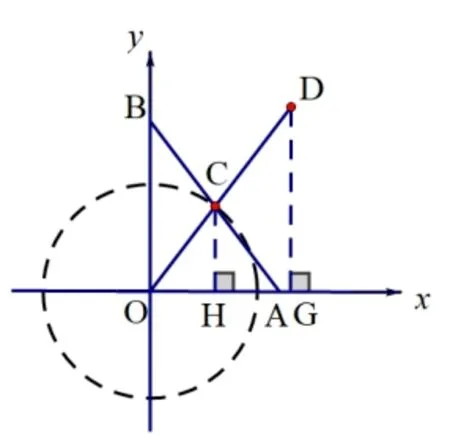
图6

解题分析: 从题中不难发现,本问题与例题异曲同工,问题以更直观的平面直角坐标系来描述两点之间的位置关系,求OC+CD取得最小值时点C.问题的关键在于定点D与定长线段AB中点E间的距离关系,显然,点E的运动轨迹在以点O为圆心,以斜边AB长度的一半为半径的圆弧上,利用三角形三边关系可知,OC+CD ＞OD(如图5),当点O、C、D共线时,OC+CD取得最小值，利用勾股定理不难求出OC+CD=OD=5,再利用ΔOCH和ΔODG相似的基本性质,可求得点C的坐标.

解如图6,因为点C是RtΔAOB斜边AB上的中点,所以OC== 2,过点O,以2 为半径作圆,连接OD,交⊙O于点C.分别过点C、点D作CH⊥x轴于点H,DG⊥x轴于点G.

因为点D为(3,4),所以OG=3,DG=4,在RtΔDOG中,OD=当点O、C、D共线时,OC+CD取得最小值, 最小值为OD= 5.又因为∠COH= ∠DOG, ∠CHO= ∠DGO= 90°, 所以ΔOCH∽ ΔODG.所以即解得所以此时点C的坐标为

拓展思考: 若把上述条件中“当OC+CD最小时”改为“当OC+CD取得最值时”,结论会发生怎样的变化呢?

变式2如图7, 在ΔABD中, ∠ABD= 90°,AB=BD= 4,点A和点B分别在x轴和y轴上运动,求在运动过程中OD的最大值.

图7

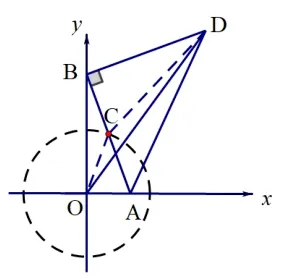
图8

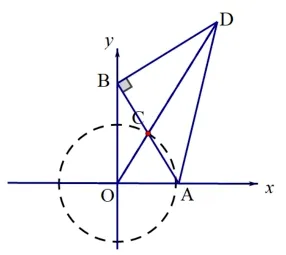
图9

解题分析: 从题中不难发现,ΔAOB和ΔABD都是直角三角形,且在点A和点B运动过程中斜边AB为定长,与变式1 区别在于点D的位置会随着AB的运动而变化,求点D的运动轨迹似乎太困难,我们不妨从其他地方入手.如图8,点D的位置取决于AB的位置,动线段AB长度为定值,且为RtΔAOB的斜边,则AB的中点C必在⊙O上,半径r= 2.在ΔOCD中我们知道,OC+CD ＞OD,所以当点O、C、D三点共线时,OD=OC+CD,此时OD有最大值(如图9).

解如图8, 在AB上找出它的中点C, 连接OC、CD,因为在RtΔAOB中,AB= 4, 所以OC=BC=AC== 2.在RtΔBCD中,BC= 2,BD=AC= 4,所以CD=当点O、C、D三点共线时,OD有最大值,OD=OC+CD=2+

拓展思考: 在运动过程中,OD有最小值,如果有,求出它的最小值.

变式3如图10,在平面直角坐标系xOy中,点A(6,0)和点B(0,8)分别在x轴和y轴上,点C为⊙A上的一个动点,已知⊙A的半径为4.连接BC,点D为BC的中点,求点D到原点O的最值.

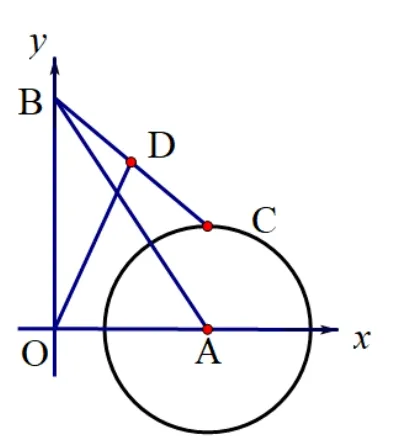
图10

图11

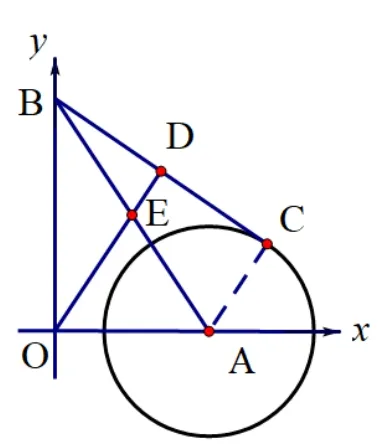
图12

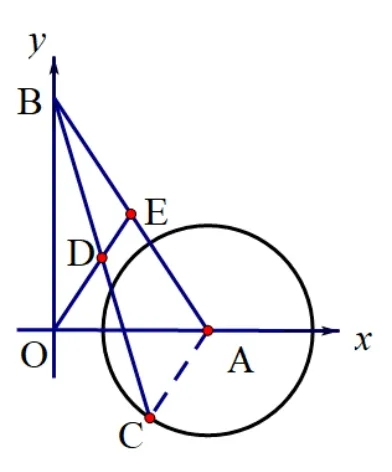
图13

解题分析: 这个问题讨论的是定点O和从动点D间的最短距离.从题中我们可以发现,ΔAOB是一个确定的直角三角形,点C为⊙A上的动点,自然可以联想到点D为BC上的从动点,且点D的位置随着点C绕⊙A运动的过程而发生改变,所以所求线段OD也是动线段.如图11,从题目已知点D为BC的中点,ΔABC与RtΔAOB存在公共边AB且AB为RtΔAOB的斜边,我们不妨大胆在AB上找出它的中点E,易知DE为ΔABC的中位线,OE为RtΔAOB斜边上的中线,OE和DE的长不难求得, 再利用三角形三边关系得出OE+DE ＞OD, 当点O、E、D三点共线时,OD取得最值(如图12、13).

解如图11,连接AC,取AB得中点E,连接OE、DE.因为点D为BC的中点,点E为AB的中点,所以DE//AC,DE== 2.在RtΔAOB中,OA= 6,OB= 8,所以AB== 10,OE== 5.在ΔDOE中, 根据“三角形两边之和大于第三边”可知:OE+DE ＞OD.

(1)如图12,当点O、E、D三点共线,且点E在线段OD上时,OD有最大值,此时OD=OE+DE=5+2=7;

(2)如图13,当点O、E、D三点共线,且点D在线段OE上时,OD有最小值,此时OD=OE −DE=5−2=3;所以点D到原点O的最大值为7,最小值为3.

拓展思考: 若点A和点B分别是坐标轴上的动点,运动过程中保持AB= 10,其他条件不变,此时BC边上的中点D到原点O的距离是否存在最值? 最值是多少?