层层递进,深入探究——以一道浙江中考题为例

浙江省杭州市杭州外国语学校(310023) 傅旭丹

2020 年杭州市的中考第23 题跟2019 年一样仍然是圆的综合题型,难度较大,需要学生有一定的数学积累以及技巧性的处理.笔者与学生一起,在课堂上探究本题的多种解法时作了几个变式拓展,记下与同行分享.

1 原题呈现

(2020 杭州市中考)如图1,已知AC,BD为⊙O的两条直径, 连接AB,BC,OE ⊥AB于点E, 点F是半径OC的中点,连接EF.

(1) 设⊙O的半径为1, 若∠BAC=30°,求线段EF的长.

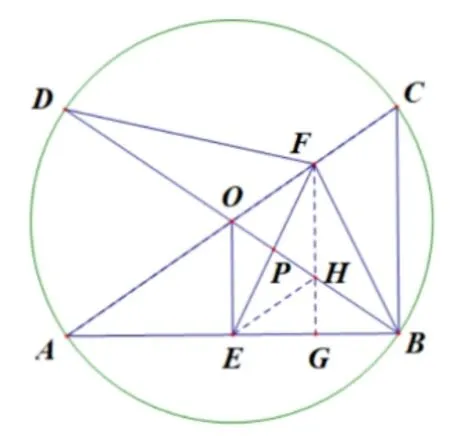
图1

(2)连接BF,DF,设OB与EF交于点P,

①求证:PE=PF.

②若DF=EF,求∠BAC的度数.

由于第一小题比较容易,笔者着重探究第二小题两问的解法与变式.

参考答案: ①作FG ⊥AB于点G, 与BO交于点H,连接EH.通过证明OE与FH平行且相等可得四边形OEHF是平行四边形, 故PE=PF.②由于FG平行于OE、BC,F为OC中点, 故FG既是高线又是中线, 所以EF=FB=DF;又O是BD的中点,因此FO ⊥BD,于是∠BAC=45°.

2 解法探究

这是一道平面几何综合题,命题者将辅助线、特殊三角形和圆的基本性质完美地结合在一起,比以往中考题更加灵活.参考答案看起来简洁明了,似乎难度并不大.但学生不一定能马上想到辅助线,进入既定“轨道”.笔者引导学生一起思考并补充,整理了几种不同解决方案.

方案一:

①如图2, 取OA中点I, 连接IE.由I、E分别是OA、AB的中点可得IE平行于OB; 再由O是IF的中点可知,P平分EF, 即PE=PF.

②过点F作FG ⊥AB于点G,做法与参考答案一样.

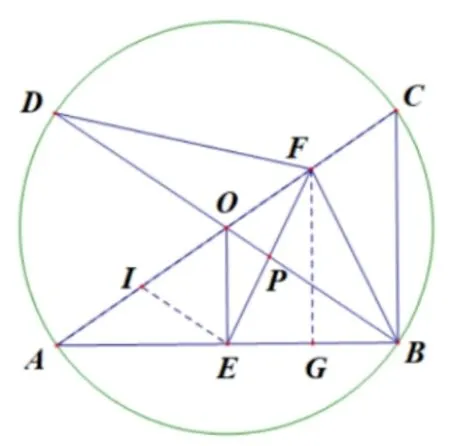
图2

以上最后一问的解法,关键在于证明EF=BF.由此笔者整理了以下两种通过构造全等三角形来证明线段相等的方案.

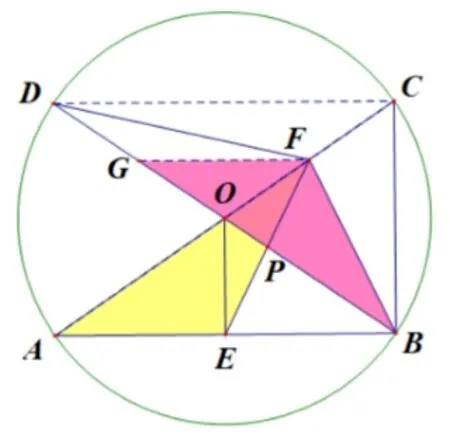
图3

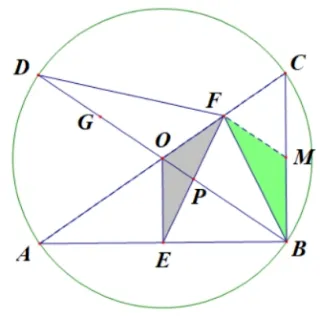
图4

方案二:

①如图3, 过F作FG//AB, 连接CD.因为F是OC的中点, 故FG=由垂径定理可知,=FG,再由FG//BE得ΔFGP与ΔEBP全等,故PE=PF.

②通过SAS可证明ΔAEF∽= ΔGFB,得到EF=FB以后同参考答案.

方案三:

①同以上任何一种.

②如图4, 通过SAS可证明ΔEOF∽= ΔBMF, 得到EF=FB以后同参考答案.

事实上,不管是哪种解决方案, 学生必须先能结合所学知识找到合适的辅助线,这对很多初中生来说非常困难,此时解析法很有可能可以帮上大忙.由题意可知, 四边形ABCD是矩形,所以如图5 建立平面直角坐标系.于是有以下方案.

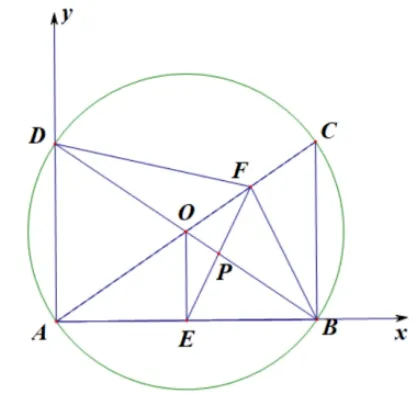
图5

方案四:

①设B(c,0),D(0,d),则C(c,d),利用待定系数法可求得直线EF与BD的解析式分别为联立求出交点为再利用两点间距离公式可得PE=PF.

②由EF=DF得因此c=d,于是∠BAC=45°.

相比之下,解析法在求证第一个结论时计算显得有些繁琐,但很快能得到第二个结论.解题过程中对学生的思维要求相对较低,不失为一种好的方案.众所周知,历年中考数学压轴题有以下设计特点: 知识点多、覆盖面广、条件隐蔽、关系复杂、思路难觅、解法灵活.一般情况我们能从多个角度来解题,涉及的知识点和方法有所不同.本题就有以上优秀压轴题应有的所有气质,不得不说命题人很高明.教师平时多给学生讲解此类问题,探究一题多解,可以在解题过程中复习巩固各项知识点,提高学生解题兴趣并提升思维品质.

3 变式拓展

在探究一题多解的同时,笔者让学生思考能否将本题做改编.可以固定题中直径AC的位置,BD在转动,由于F位置不变,E在改变,所以DF与EF的长度都随着BD发生变化.于是笔者打算探究一下DF与EF的长度之比.

接着方案四的解析法, 由于EF=当d /= 0 时,λ=因为当d= 0 时,λ= 3.综上所述,λ ∈本题最后一问就是当λ= 1 时求∠BAC的度数,那么λ取其它值时∠BAC是几度呢?

变式1已知AC,BD为⊙O的两条直径, 连接AB,BC,OE ⊥AB于点E, 点F是半径OC的中点, 连接EF,BF,DF,设OB与EF交于点P,若DF=2EF,求∠BAC的度数.(答案: tan ∠BAC=

变式2已知AC,BD为⊙O的两条直径, 连接AB,BC,OE ⊥AB于点E, 点F是半径OC的中点, 连接EF,BF,DF,设OB与EF交于点P,若∠BAC= 60°,求DF:EF.(答案:

以上两个问题用几何法解起来比较困难,解析法通过将已知条件转化为点的坐标之间的关系,能轻松解决.事实上,图形当中还有两条动线段DE与CE(DE=CE).我们同样可以探究DE与EF的长度比值对∠BAC的影响.

当d /= 0 时,κ=因为当d= 0 时,κ= 2.综上所述,κ ∈于是笔者给出以下两个变式,读者可以自行计算.

变式3已知AC,BD为⊙O的两条直径, 连接AB,BC,OE ⊥AB于点E, 点F是半径OC的中点, 连接EF,BF,DF,设OB与EF交于点P,若DF=求∠BAC的度数.(答案: 45°)

变式4已知AC,BD为⊙O的两条直径, 连接AB,BC,OE ⊥AB于点E, 点F是半径OC的中点, 连接EF,BF,DF,设OB与EF交于点P,若∠BAC= 60°,求DE:EF.(答案:

做完以上变式, 学生继续挖掘原题中可以变化的条件,提出如果将F变为线段OC的三等分点,我们是否可以做相应的探究呢?

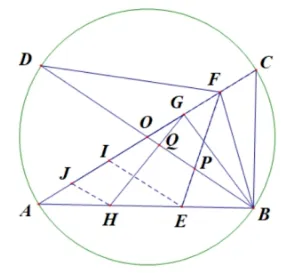
图6

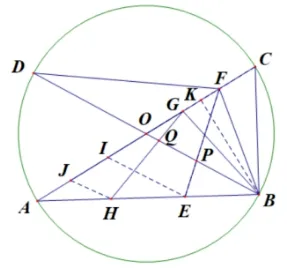
图7

图8

如图6,F,G是OC的三等分点,E,H是AB的三等分点.找到线段OA的三等分点I,J, 连接IE,JH.根据平行线分线段成比例定理不难证明FP:PE= 2 : 1,GQ:QH=1:2.与F为OC的中点时同理,我们可以证明图中EF=FB,于是当DF=EF时∠BAC= 45°.事实上,若DG=GH,∠BAC大小不变.这些探究学生自己能完成,如果探究到此为止,那么也就跟原题大同小异并没有什么新意.笔者发现图中GH与GB长度也相等,那么GH和EF的长度有何关系呢?

变式5已知AC,BD为⊙O的两条直径,连接AB,BC.E,H是AB的三等分点,点F,G是半径OC的三等分点,连接EF,BF,DF,GH,GB, 设OB与EF、GH分别交于点P、Q.

(1)求证:FP:PE=2:1,GQ:QH=1:2.

(2)若DF=EF,求∠BAC的度数.

(3)若GH=EF,求∠BAC的度数.

关于第三问, 当GH=EF时,BF=BG.过B作BK ⊥OC于点K,则K为FG的中点.设CK=a, 则AK= 3a,由射影定理可得BK=于是tan ∠BAC=故∠BAC=30°.更一般地,我们有如下结论.

推论如图8, 已知AC,BD为⊙O的两条直径,连 接AB,BC.E1,E2,··· ,En−1是AB的n等分点,点F1,F2,··· ,Fn−1是半径OC的n等分点,设OB与E1F1,E2F2,···En−1Fn−1分别交于点P1,P2,··· ,Pn−1.则有以下结论:

①FiPi:PiEi=(n −i):i,其中i=1,2,··· ,n −1.

②若DF=EiF i(i=1,2,···n −1), 则∠BAC=45°.

③n为奇数时, 若对于某个i= 1,2,··· ,有EiF i=En−iFn−i, 则∠BAC= 30°;n为偶数时, 若对于某个i= 1,2,··· ,−1, 有EiF i=En−iFn−i, 则∠BAC=30°.

4 一点反思

对于一线教师来说,中考、高考题是不可多得的宝贵资源,如何用好这个资源是我们永恒的课题.真题是考试的精华所在, 它将考试范围内的知识点以题目的形式展现出来,这也是命题专家智慧的结晶.真题充分体现该题命题思路和意图,教师应该带领学生通过分析题目的关键要点,了解相关内容的意义,学会从命题者的角度分析问题,寻找解决问题的切入口,培养“题感”.要在课堂上讲好一道题,教师需引导学生从多方面思考问题,找到多种解题方法,从而尽可能全面地复习所学知识点.比如用几何法解本题时,要求学生有非常强的应变能力,灵活度大.此时看看能否建立直角坐标系,将平面几何问题转化为点、线段、角度的计算问题,思维上的要求就低了很多.同时,也可以让学生尝试改编题目,自己编、自己解,这种体验非常有意思.学生提出将中点改成三等分点后,相应问题的探究其实跟之前大同小异.学生可以再次理清求证思路,加深理解.教师在此基础上,可以适当开拓新的问题,这样不仅可以激发学生的解题兴趣,也更有解题的成就感,提高思维的灵活度.另一方面,教师也能在教学活动中积累“功力”,提升专业素养.