基于目标的相机标定方法

王利华 李亮亮 郭恒林

(山东科技大学 测绘科学与工程学院, 山东 青岛 266590)

0 引言

随着计算机视觉和数字摄影测量的发展,基于视觉的坐标测量技术得到了更广泛地应用。相机的内参和光学畸变系数被用于描述相机自身特性,是精确获取被测物体的三维坐标的前提。通过一定的方法和手段获取相机内参和光学畸变系数的过程就是相机标定。

相机标定方法根据标定方式的不同,主要可以分为两种:自标定方法和基于目标的标定方法[1]。自标定方法存在约束性较差[2]、对噪声敏感等缺点[3-4]。因此,基于目标的相机标定方法,仍具有重要的作用。基于目标的相机标定方法是指用一个结构已知、精度很高的标定物或控制场作为空间参照物,通过空间点和影像点之间的对应关系来建立相机参数约束,然后通过优化算法来求取这些参数[5]。基于目标的相机标定方法主要包括计算机视觉中的张正友标定法和摄影测量中基于直接线性变换(Direct Linear Transformation, DLT)、空间后方交会的标定法。张飞[6]和靳冲[7]等主要针对计算机视觉中的相机标定方法做了比较与分析,王冬[8]主要对摄影测量中相机标定做了研究与分析。本文针对上述3种方法进行了研究分析。

1 基于目标的相机标定方法原理

1.1 后方交会标定法原理

由摄影测量中的共线方程出发,再根据空间后方交会原理并考虑光学畸变,可以得到空间后方交会相机标定的误差方程:

V=AXe+BXi+CXd-L

(1)

式中,Xe是外方位元素;Xi是内方位元素;Xd是畸变系数;A、B、C为对应的系数矩阵;L是系数矩阵。利用物点坐标和对应的像点坐标迭代求解,可以得到需要标定的参数。

1.2 直接线性变换标定法原理

根据摄影测量中的共线方程,考虑到光学畸变,可以导出多余观测下直接线性变换的基本关系式:

(2)

式中,(x,y)是像点坐标;(vx,vy)是像点坐标对应的误差值;(Δx,Δy)为光学畸变;(X,Y,Z)是像点对应的物方坐标;li是关于内外方位元素的函数。

先利用直接线性变换的直接解法求取初值再利间接平差进行迭代求解即可求取li和畸变系数,再根据等式(3)即可求得相机内参。

(3)

1.3 张正友标定法原理

张正友标定法[9]从计算机视觉中的相机模型出发,结合相机的单应性矩阵并利用标定板作为控制场求解相机的畸变系数和内部参数。

设光学相机模型为:

(4)

则有:

[h1h2h3]=λA[r1r2t]

(5)

根据旋转矩阵的正交性有:

(6)

根据单应性矩阵H再利用等式(6)可以求取内外参数的初值,再计算畸变系数。

2 实验设计与结果分析

2.1 实验设计

3种相机标定方法对控制场的要求不同,其中空间后方交会和直接线性变换都是基于三维控制场,而张正友标定法采用二维控制场。对于三维控制场选择山东科技大学高精度相机标定场,二维控制场选择高精度的标定板。本次实验所采用的相机为Canon200D,此相机为非量测型相机,其分辨率为6 000×4 000个像素,传感器尺寸为22.3 mm×14.9 mm,镜头型号为:Canon EF-S 18-55 mm f/4-5.6 IS STM。

2.1.1 空间后方交会和直接线性变换标定法实验设计

基于空间后方交会和直接线性变换的相机标定方法都需要精确的三维空间坐标。本次实验采用徕卡TM5100A经纬仪工业测量系统,其测角精度为0.5″。通过该测量系统对三维控制场的394个控制点进行精确测量,同时采用Canon200D相机对控制场拍摄3～5张像片,从中选择成像质量最好的单张像片作为实验照片。

2.1.2张正友标定法实验设计

在张正友标定法中根据标定板的设计值,选取其角点作为二维控制点。本次实验采用8×8的标定板,其单元网格大小为75 mm×75 mm。将该标定板固定在平面上,利用Canon200D相机从各个方向对标定板进行拍摄,像片数量在20～30张,以达到最佳标定效果[10]。

2.1.3程序设计

本文针对3种不同的标定方法,根据上述理论介绍并结合实际使用需要,在VC++环境下对空间后方交会和直接线性变换方法进行实现,对于张正友标定法采用MATLAB相机标定工具箱进行实验。

2.2 三种相机标定方法的结果分析

2.2.1空间后方交会标定结果比较分析

将镜头分别设置为18、35、55 mm 3种不同的焦距进行像片数据采集,随机选取20个控制点,利用空间后方交会程序对相机参数进行计算。对于径向畸变和切向畸变,其高阶改正分量不但不能提高精度,反而引起解的不稳定性[11],这里只取前2项。同时,为了比较不同焦距下的镜头畸变情况,选取像点A,令其像素坐标为(500,500), 利用标定结果中的畸变系数计算A点坐标畸变改正值(Δx,Δy),结果如表1所示。由表1可以发现,随着焦距的增大,畸变改正值的绝对值总体呈现先减小后增大的趋势。在使用常规镜头时,为了保证镜头畸变比较小,应当适当选择焦距大小。

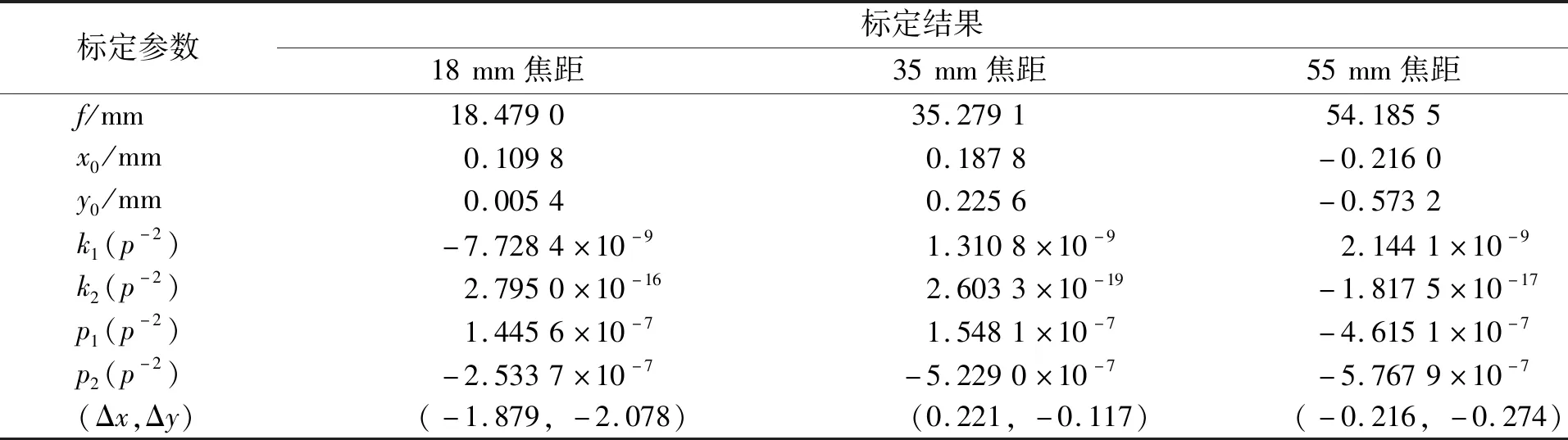
表1 不同焦距的空间后交标定结果

将焦距固定在18 mm附近,随机选择数量不同的控制点,其空间后方交会标定结果及中误差如表2所示。由表2可以发现:随着控制点数量的增加,相机内方位元素和畸变系数并没有明显的变化,说明如果随机选择10个控制点,其解算结果已经比较可靠。但是参数之间往往具有相关性[12-13],为了避免解的强相关性,可以选择多于10个点。其次,随着控制点数量的增加其解算精度并没有提高。这主要受到像片中控制点坐标精度的影响。在三维控制场中,所有点的成像质量不可能完全一致,特别是在景深较大的时候,很难保证边缘控制点的成像质量。因此,在利用空间后方交会进行相机标定时,控制点应尽量随机分布,且控制点数量不宜过多。

表2 不同控制点数量的空间后方交会标定结果

2.2.2 直接线性变换与空间后方交会标定结果比较分析

对于直接线性变换和空间后方交会,分别设置18、35、55 mm焦距,并分别选取同一组像片上的相同控制点,利用多组数量不同的控制点进行实验,焦距大小、控制点数量、标定参数单位权中误差之间的关系如图1所示。

根据表2得到的结论可知,控制点的选取不宜过多。由图1可以发现:在控制点数量为15的情况下,直接线性变换的标定精度总体上优于空间后方交会的标定精度。

图1 焦距大小、控制点数量与精度的关系

此外,随着焦距的增大,无论是直接线性变换还是空间后方交会,其标定精度基本都有所降低。这是由于随着焦距的增大,景深逐渐变小,同时视场角也有所减小,前者会严重影响像片中控制点标志的成像质量,后者会影响控制点的数量和分布。因此,在焦距增大时,直接线性变换和空间后方交会标定方法均存在一定程度上精度下降的问题。

2.2.33种标定方法标定结果比较分析

将相机焦距固定在18 mm附近,利用3种方法分别进行相机标定。其结果如表3所示。

由表3的结果可以发现:在内方位元素上,张正友标定方法结果略大于其余两种方法的结果,就精度而言,张正友标定法的精度低于其他2种方法。

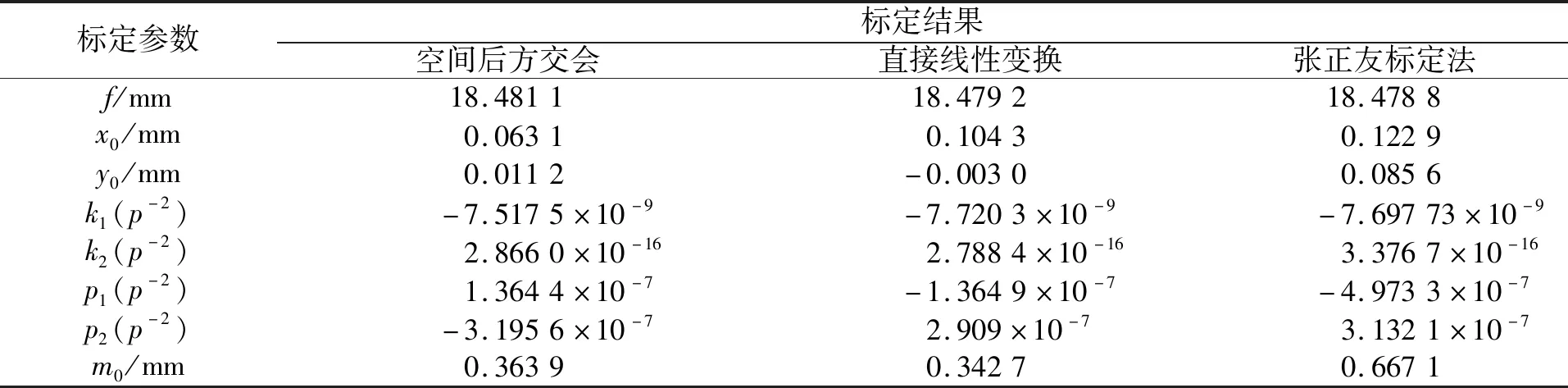
表3 3种方法标定结果

3 结束语

本文针对基于目标的相机标定3种常用的方法:摄影测量中的空间后方交会和直接线性变换标定法、计算机视觉中的张正友标定法,介绍其相关理论,并通过实验数据分析了3种方法在焦距、控制点数量、精度方面的特点。可以得出如下结论:

(1)对于空间后方交会标定方法而言,控制点应尽可能随机分布且控制点数量在15个左右为宜,过多的控制点反而会使得精度下降。

(2)随着焦距的增加,直接线性变换和空间后方交会标定精度均有所降低。

(3)直接线性变换标定方法、空间后方交会标定方法、张正友标定方法的标定精度依次降低。

(4)张正友标定法具有很好的便捷性,但影响精度的因素很多,稳健性不如其他2种方法。直接线性变换标定方法无须初值,而空间后方交会则需要设置合理的初值,若初值不合理,可能会导致解算结果错误甚至无法解算出结果。