基于Python的开采沉陷预计算法
2021-04-20刘吉波王志红任传建
刘吉波 王志红 任传建
(贵州工程应用技术学院 矿业工程学院, 贵州 贵阳 551700)
0 引言
沉陷预计可以在地下资源采出前掌握地表破坏情况,在矿山资源开发利用中具有非常重要的作用。概率积分法是目前较为成熟,应用广泛的预计方法,已有很多预计软件,多是采用Visual C++、C#、Visual Basic.NET等软件平台开发[1-6],也有采用Matlab、AutoCAD、ArcGIS等进行二次开发实现的[7-10]。
Python是一种跨平台的计算机程序设计语言,是结合了解释性、编译性、互动性和面向对象的脚本语言,具有免费、可移植、功能强大、易于使用的特点。Python除了math等标准程序库外,还提供了大量成熟的专业程序包,其中numpy和scipy主要用于科学计算,sympy程序库具有符号计算功能[11-15]。
本研究利用scipy模块的积分功能实现了开采沉陷预计计算,对算法进行了优化设计,并采用matplotlib模块实现了等值线绘制。
1 利用Python进行概率积分预计的基本算法
1.1 地表任意点移动变形概率积分计算公式[16-17]
概率积分法地表下沉值计算公式为:
(1)
式(1)中,Wmax为地表充分采动时的最大下沉值;r为主要影响半径;D为开采区域;X、Y为预计点地面坐标。倾斜、水平移动、曲率等变形可依据下沉公式计算而得。
1.2 scipy积分计算功能及精度分析
scipy模块提供了丰富的积分运算,其中integrate子模块包含一重、二重及三重积分函数,二重积分可以用dblquad函数计算。dblquad的一般调用形式是dblquad(func,a,b, gfun, hfun),其中,func是待积分函数名,b、a是x变量的上下限,hfun、gfun为定义y变量上下限的函数名。dblquad函数的返回值是一个tuple类型的变量(result, abserr),result是积分结果,abserr是积分误差。
import scipy as sp
def func(y,x):
return sp.exp(-x-y)
gfun=lambda x:0.0
hfun=lambda x:x
(a,b)=(0.0,2.0)
value=sp.integrate.dblquad(func,a,b,gfun,hfun)
print(“%.3f”% value[0])
上述代码输出为0.374,计算误差小于4.0×10-15,scipy的dblquad函数积分精度很高,满足沉陷预计要求。
1.3 利用scipy实现概率积分预计
概率积分法适用叠加原理,故对开采区域进行相应划分后,可使每个子开采区域符合积分计算要求。因开采区域一般是由多条线段构成的多边形,故边界可用直线方程表示。为简化问题,以单一区域开采下沉预计为例进行研究。
设有一水平工作面,煤厚m=3.0 m,下沉系数q=0.7,开采深度H=200.0 m,主要影响角正切tanβ=2.0。X方向位于区间[300 m,1000 m],Y方向位于直线y1=0.1x+270和y2=0.1x+470之间,地面预计格网左下角坐标为(0,0),网格间距20 m,X方向65个网格,Y方向40个网格。
为确保程序通用性,上述工作面开采地表下沉计算的程序实现为:
import scipy as sp
(m,q,tanb,H)=(3.0,0.7,2.0,200.0)
(W0,r)=(m*q*1000,H/tanb)
(x1,x2)=(300.0,1000.0)
y1=lambda x:a1*x+b1
y2=lambda x:a2*x+b2
(a1,b1,a2,b2)=(0.1,270,0.1,470)
(nx,ny,dx,dy)=(65,40,20,20)
(X0,Y0)=(0,0)
(Xn,Ym)=(X0+(nx+1)*dx,
Y0+(ny+1)*dy)
data=[]
for X in range(X0,Xn,dx):
for Y in range(Y0,Ym,dy):
def pintegral(y,x):
return sp.exp(-sp.pi*(((x-X)/r)
**2+((y-Y)/r)**2))/(r*r)
c=sp.integrate.dblquad(pintegral,
x1,x2,y1,y2)
data.append([X,Y,W0*c[0]])
根据预计结果,绘制下沉等值线图。
1.4 预计点密度选择
利用概率积分法进行地表移动变形预计时,预计点的密度对于预计效果和运行效率至关重要。密度过小,虽用时短,但精度会大幅降低,导致变形等值线呈现剧烈的锯齿状;密度过大,精度高,但预计耗时多,预计工作面多,预计区域范围大时影响更大。根据试验,一般情况下网格密度50 m×50 m时即满足需要,当要求较高时可适当增加网格密度,反之网格密度可降低。
2 预计算法优化
2.1 积分函数构造
Python的符号计算模块sympy、科学计算模块scipy、数值计算模块numpy和数学函数模块math中都定义了指数函数exp。在其他条件不变情况下,选用不同模块的exp函数构造积分函数,程序运行时间有很大差异,如表1所示。从表1可以看出采用math模块的exp比scipy的计算效率提高1倍,numpy和scipy的效率相当,而sympy因要进行符号运算,效率极低,不建议采用。

表1 不同exp计算时间(循环内部)
将预计点X、Y坐标定义为全局变量,积分函数定义于循环体之外,程序运行时间如表2所示。通过表2和表1可知,程序性能提高1倍左右。

表2 不同exp计算时间(循环外部)
2.2 利用通用函数提高效率
numpy模块提供了通用函数功能,其具有与输入数组形状相同的输出数组,可以一次性对所有数组数据进行计算[12-13],避免了循环操作,从而提高程序计算效率。通过vectorize函数可以快速创建通用函数。
#定义通用函数
def cal(n):
(row,col)=(int(n/(nx+1)),n-row*(nx+1))
(X,Y)=(X0+col*dx,Y0+row*dy)
def pintegral (y,x):
return mh.exp(-mh.pi*(((x-X)/r)**2
+((y-Y)/r)**2))/r/r
c=dblquad(pintegral,x1,x2,y1,y2)
return round(c[0]*W0,0)
#预计点数组
points_array=np.arange((ny+1)*(nx+1))
#生成通用函数
vgauss=np.vectorize(cal)
#预计计算
result=vgauss(points_array)
由表3和表1可知,通用函数操作可极大提高程序性能,减少运行时间。

表3 调用通用函数运行时间
2.3 利用影响圆确定计算范围
在水平煤层开采时,对地表点A有影响的煤层开采范围是一个圆,其以A在煤层的垂直投影点O为圆心,半径R=Hctanδ0,δ0为边界角,如图1所示。只有位于圆内的煤层开采对A点有影响,圆外的煤层开采对A点影响为0。当多工作面开采尤其是土地复垦等需要进行全井田预计时,预计范围大,计算点数多,利用影响圆法可以大幅提高程序效率[14-16]。

图1 水平煤层开采对地表点的影响圆
设计工作面如图2所示,取边界角δ0=55°,则R=140.0 m。将工作面边界向外侧偏移R,得到新边界C和D,位于边界C和D内的点进行预计计算,位于C和D外的点移动变形直接赋值为0。

图2 有效预计范围确定
全部预计,共10 201个预计点,用时45 s,利用影响圆法,共2 652个预计点,用时6 s。
实际预计时,对于非水平煤层开采,可分别计算工作面走向方向、上山方向和下山方向的影响圆半径,并确定有效预计范围。
2.4 坐标系选择
在实际开采中,工作面走向经常是任意方向的,造成沉陷预计复杂性提高。将y方向预计网格数改为ny=75,选用math.exp函数,当Y积分限斜率a=0.0,即工作面走向沿X方向时,预计用时16 s;当Y积分限斜率a=1.0时,预计用时20 s,说明工作面走向与Y轴的不垂直度增加,程序用时增加。同时,对于矩形工作面,工作面需进行分割才能进行积分运算。
选择合适的工作面坐标系进行积分计算可以解决此问题。如图3所示,当工作面为矩形时,可以工作面左下角点为原点,X轴沿工作面走向方向;当工作面为非矩形时,可以令X轴沿长对角线方向;当工作面为多边形时,选最长的两点连线为X轴。此时需要将计算点坐标转化至工作面坐标系后进行积分计算。从地面坐标系到工作面坐标系转换公式为[17]:

图3 坐标系选择

(2)
其中,φ为工作面坐标系x轴顺时针与大地坐标系X轴的夹角,(X0,Y0)为工作面坐标系原点O的大地坐标系下的坐标。
3 等值线绘制
matplotlib是Python实用的图形和表格绘制软件包,可用于便捷地绘制等值线图、等值线云图和三维曲面图[15]。
绘制二维等值线图的部分代码如下,生成等值线图如图4所示。

图4 下沉等值线图
#datax,datay,datav分别存放X坐标、Y坐标和变形值
#建立三角剖分
triang=tri.Triangulation(datax,datay)
#实现等值线绘制
con=plt.tricontour(datax,datay,triang.triangles,datav,levels=listlevels,cmap='rainbow')
#标注等值线
label=plt.clabel(con, inline=False, fmt='%.0f', fontsize=20)
绘制三维下沉曲面和下沉等值线云图的部分代码如下,生成下沉曲面和等值线云图如图5所示。
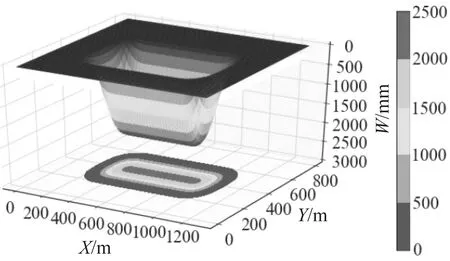
图5 下沉曲面图和下沉等值线云图
#添加绘图子窗口
ax=fig.add_subplot(111, rojection='3d')
# 设置图像z轴的显示范围
ax.set_zlim(3000,0)
#绘制下沉曲面
ax.plot_surface(X3d,Y3d,Z3d,linewidths=1, rstride=1,cstride=1, cmap=plt.get_cmap('rainbow'))
#绘制下沉等值线云图
cset=ax.contourf(X3d,Y3d,Z3d, zdir='z',
levels=vlevels,linewidths=1,offset=3000, cmap='rainbow')
4 结束语
对利用scipy的积分模块进行开采沉陷预计计算和利用matplotlib绘制等值线图及曲面图进行了研究,得出以下结论:
(1)scipy科学计算模块功能强大、高效,用少量代码即可完成复杂的概率积分预计;利用math.exp比numpy.exp、sicpy.exp及sympy.exp计算效率高;将积分函数定义于循环体外,可以进一步提升程序性能;利用通用函数进行数组整体操作可提高计算效率。
(2)多工作面大范围预计时,利用影响圆法可以大幅减少参与计算的点数;合理选择坐标系、设计预计点密度也能提高程序性能。
(3)利用matplotlib绘图模块,可以快捷绘制变形等值线图、等值线云图或三维曲面图,图形美观实用。
