利用特征点采样一致性改进ICP算法点云配准方法

宋成航 李晋儒 刘冠杰

(山东科技大学 测绘科学与工程学院, 山东 青岛 266590)

0 引言

随着点云数据处理技术和计算辅助设计技术的不断进步,点云配准技术成为计算机视觉和图像处理的重要研究方向。该技术在三维重建[1]、医学[2]、计算机视觉[3]等领域得到广泛的应用。目前,应用最广泛的点云配准方法是由Besl和Mckay等[4]于1992年提出的最近点迭代算法(Iterative Closest Point,ICP),该算法的基本原理是在两组点云数据之间寻找对应点对集,通过不断迭代计算两片点云之间的变换矩阵,获取目标点云集和源点云集之间的对应关系[5]。传统的ICP算法存在计算效率低和配准初始位置要求高,容易陷入局部最优等问题。因此,相关学者大多采用初始配准的方法获得良好的初始位置,并在传统ICP方法的基础上进行大量的改进算法研究。根据两片点云表面局部几何特征查找点对点的对应关系,例如旋转图像(Spin Images,SI)[6]、方向直方图特征(Signature of Histograms of Orientations,SHOT)[7]、点特征直方图(Point Feature Histograms,PFH)[8]及改进的快速点特征直方图(Fast Point Feature Histogram,FPFH)[8-9]等,但对于密度较大的点云,计算每个点的特征,很大程度影响点云的配准效率。文献[10]通过采样一致性算法(Sample Consensus Initial Alignment,SAC-IA)对两片点云的特征点进行配准;文献[11]基于全局搜索对应点利用四点法(4-Points Congruent Sets,4PCS)算法进行点云配准文献[12]提出一种正态分布变换(Normal Distribution Transform,NDT)算法点云配准方法。这些方法配准效率高,但是稳定性差,配准精度低。

根据上述配准方法存在的问题,本文提出一种基于特征点采样一致性改进ICP算法点云配准方法。首先将2片点云数据体素下采样后,根据点云法向量邻域夹角均值提取特征点并通过FPFH进行特征描述,然后采用SAC-IA算法粗配准计算出点云的初始坐标变换矩阵,使点云获得良好的初始位置,最后通过K维树改进ICP算法进行精确配准,有效地解决传统ICP算法易陷入局部最优和收敛速度慢的问题。

1 算法介绍

针对传统ICP算法存在收敛速度慢,容易陷入局部最优等问题,提出一种基于特征点SAC-IA改进ICP算法点云配准方法,算法流程如图1所示。首先对点云进行下采样,减少点云数量,其次计算点云的法向量邻域夹角和FPFH,用于提取点云数据的特征点和特征描述;然后通过SAC-IA粗配准得到特征点之间的对应关系,完成2片点云的初始坐标变换,进而实现点云的初始配准,使2片点云获得良好的初始位置;最后采样用K维树邻近搜索算法加速对应点的查找,提高计算效率,并计算出对应点的刚体变换矩阵,完成点云精确配准。

图1 本文算法流程图

2 点云粗配准

2.1 提取特征点

在初始配准之前,由于点云数据量较大,导致配准效率降低,因此本文对原始点云进行下采样,有效减少点云数量,提高配准效率。针对点云粗配准,先利用不同邻域半径估计点云的法向量,并根据法向量邻域夹角提取特征点,本文使用主成分分析(Principal Component Analysis,PCA)的方法估计点云的表面法向量。

点云数据任意一点Pi的法线估计近似于估计表面的一个相切面法线,即最小二次拟合平面,该平面的法向量为对应点处的法向量。为了保证该点处切平面为最下二乘拟合平面,分析一个协方差矩阵的特征矢量和特征值,对应的协方差矩阵C如下:

(1)

如图2(a)所示,局部区域的点云法向量夹角较大,则表明该区域较为起伏;相反如图2(b)法向量夹角变化不大则表明该区域较为平坦[13]。因此,定义点云某一点Pi与其邻近点法向量夹角的算术平均值:

图2 特征区域与非特征区域法向量夹角

(2)

式(2)中,θij为点云Pi与邻近法向量的夹角。

根据点Pi与其邻近点法向量的夹角来提取特征点,选取适当的阈值ε,当fi>ε时,点Pi处弯曲程度较大,故Pi为特征点;当fi<ε时,点Pi处较为平坦,故Pi为非特征点。

为保证点云表面法向量方向的一致性,提取特征点更准确,需要对求得的法向量进行方向调整[14],使之满足公式(2)。

ni·nj<0,(i≠j)

(3)

式(3)中,ni为源点云法向量,nj为目标点云法向量。

2.2 FPFH特征描述

根据点云法向量夹角特性提取特征点后,通过FPFH对特征点进行描述。FPFH是通过提取特征点的邻域几何性进行局部特征描述的方法,它通过点云的法向量和邻域点的表面曲率构建一个特征直方图[15],从而快速确定特征点之间的对应关系。实际上它是由PFH改进而来。PFH是根据对应点对的欧式距离和法向量的几何关系计算出特征点与源点云之间的对应关系,并形成一个多维特征直方图对点的K邻域进行几何描述。其点Pq的PHF邻域特征影响范围如图3所示。

图3 点Pq的直方图邻域特征影响范围

已知点云P中有n个点,那么它的PFH计算复杂度是O(nk2),其中,k是点P云中每个点计算特征向量时的邻域数量。由于密集点云的特征直方图的计算量过大,为了减少计算复杂度,本文提出FPFH算法,计算特征点Pq在以r为半径的源点云邻域内的几何关系,将计算复杂度降到O(nk),仍然保留了PFH的识别特性,同时增加了邻域特征范围。点的FPHF邻域特征影响范围如图4所示。

图4 计算特征点Pq的FPHF领域特征影响范围

FPFH具体计算步骤如下:

(1)计算特征点Pq和邻域点之间的特征元素,构建简化的点特征直方图(Simple Point Feature Histograms，SPFH);

(2)确定每个点的K近邻域,利用SPFH值来计算Pq的FPFH特征,如公式(4)所示:

(4)

式(4)中,fFPFH为快速点特征直方图描述子,wk为权重,即表示特征点Pq到邻域点Pk的距离。

2.3 SAC-IA算法粗配准

在点云粗配准过程中,为了满足配准的前提条件,先利用单位四元素法计算点云配准初值,将源点云P的所有点Pi转换到目标点云Q所在的坐标系下,即

(5)

式(5)中,Rz为旋转矩阵,XT为平移向量。

当点云初始位置偏差较大时,配准的过程中容易陷入局部最优。为了解决这一问题,通过SAC-IA算法对点云进行初始配准,实现2片点云初始坐标变换,同时根据点云的法向量和FPFH特征描述提高变换矩阵的估计质量和配准的精度,其具体算法步骤如下:

(1)选取采样点:从源点云P中选取n个采样点,为了保证采样点具有不同的FPFH特征,采样点之间的距离应满足大于最小距离阈值d。

(2)对应点查找:从目标点云Q中查找与点采样点相似的FPFH特征的一个或多个点,并将这些相似点作为在点云Q中采样点的对应点。

(6)

其中,t1为设定值;li为变换后第i组对应点的距离差。该算法较结果依赖参数的设定,例如初始配准时最小采样的距离、计算法向量和建立FPFH邻域的大小。根据对应点变换选取最优解,使点云配准距离误差达到最小,获得最终刚体变换矩阵,完成初始配准。

3 改进ICP算法

经过SAC-IA算法粗配准后,源点云和目标点云已经大致的重合在一起,但配准的精度较低,为了进一步提高配准的精度,在此基础上采用改进的ICP算法进行精确配准。本文在传统ICP算法精确配准的基础上使用K维树邻近搜索算法进行优化,加速查找对应点对,有效地提高了计算效率。

K维树[16]是一种分割K维数据空间的数据结构,用来表示K维空间中的点集合。传统ICP算法在重复迭代搜索最近点过程中消耗大量时间,使计算效率降低。所以使用K维树进行搜索对应点,可以有效地减少计算复杂度,实现邻域关系的快速查找。

ICP算法原理将待配准点云转换到目标点云所在的坐标系下,根据几何关系计算坐标变换参数R(旋转矩阵)和T(平移向量),使得2片点云数据变换后的距离最小。当待配准点云与目标点云经过不断旋转与平移,从而达到目标函数最小,即满足最小二乘定理时,那么配准效果达到最优[17]。

经过粗配准坐标变换的源点云P′和目标点云Q作为输入点云进行ICP算法精配准,其具体算法步骤如下:

(1)将初始配准后的点云P′(经过坐标变换后的待配准点云)和目标点云Q,作为精配准的初始点集;

(2)对待配准点云P′所有点Pi,在目标点云Q中寻找距离最近的对应点qi,作为该点在目标点云中的对应点,组成对应点对;

(3)计算旋转矩阵R和平移向量T,使对应点对之间的均方误差dk最小,其中:

(7)

(4)设定阈值ε(即dk-dk+1<ε)和最大迭代次数Nmax。

将上一步得到的刚体变换作用于源点云P′,得到新点云P″,并计算P″和Q的距离误差,如果两次迭代的误差小于阈值ε或者达到最大迭代次数大于Nmax,则迭代结束,不然更新初始配准的点集为P″和Q,重复上述步骤,直至满足收敛条件。

4 实验结果与分析

为了验证上述点云配准方法的有效性,本文实验平台为:处理器i3-4005U CPU@1.70GHz,内存8GB的Win7系统,并使用Visual C++结合PCL进行编程。采用斯坦福大学开放三维点云数据库中不同视角下的Bunny点云数量分别为28 869、29 491的Dragon点云数量分别为28 869、29 491进行验证。

4.1 特征点提取结果

本文采用两个组点云数据密度较高,所以在保留原始点云特征的基础上,对原始点云进行下采样,并利用不同邻域半径估计点云的法向量,通过计算Bunny和Dragon点云数据与邻域之间的法向量夹角,设定法向量夹角阈值ε=5,其法向量夹角均值大于阈值即为特征点,反之为非特征点。文献[13]与本文提取特征点的结果对比如图5所示。

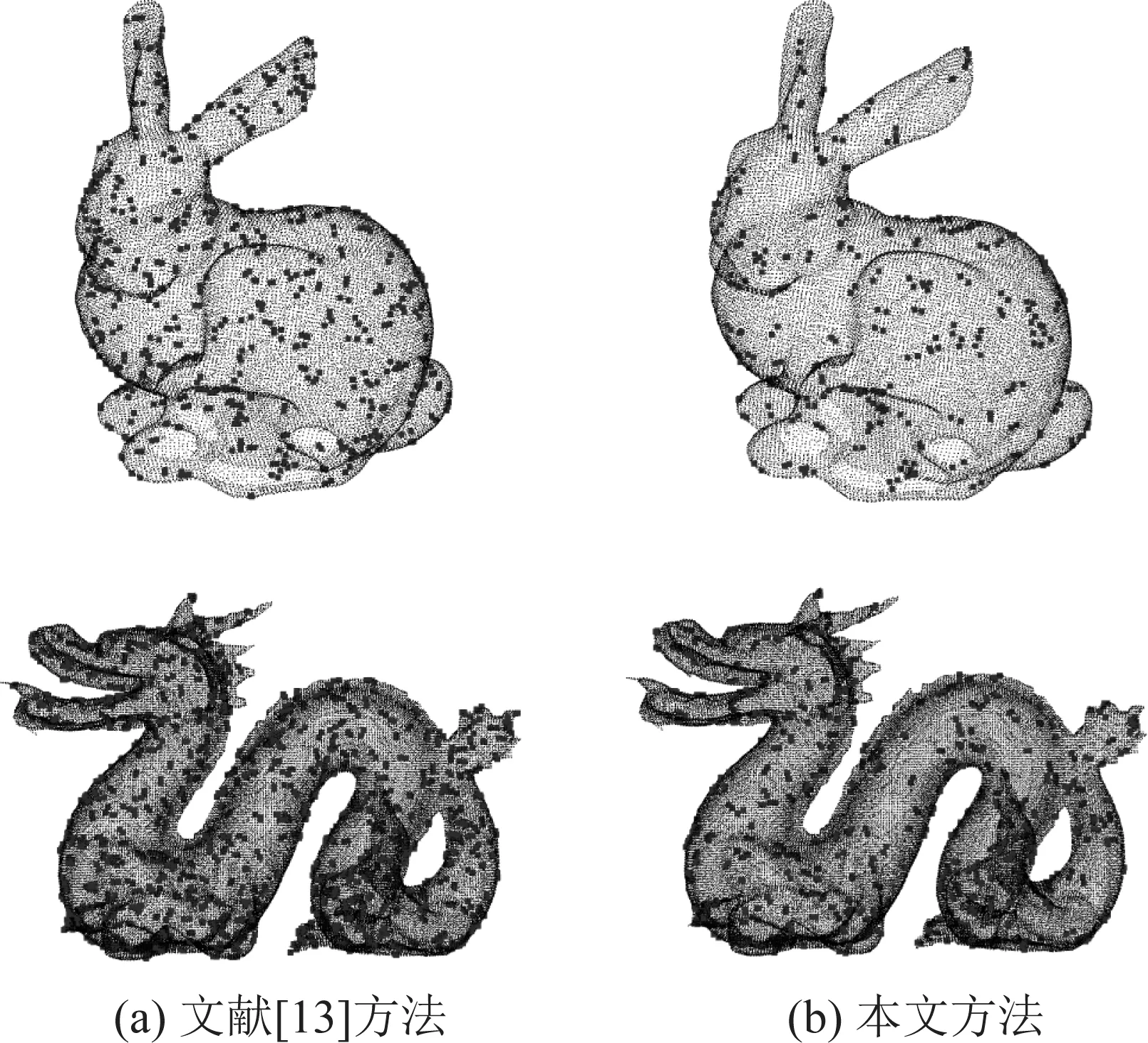
图5 特征点提取结果对比

从图5(a)中可以看出文献[13]提取的特征点过多且分布密集,不利于后续的点云配准,然而本文在下采样后,有效地减少点云的密度,提取的特征点较为稀疏且保留了原始点云的体表特性。

4.2 点云配准分析

根据法向量夹角特性提取特征点后,在半径为0.05 m范围内的所有邻元素进行FPFH特征描述,最后通过SAC-IA算法进行粗配准,计算出初始坐标变换矩阵,完成粗配准，配准结果如图6所示。从图6中可以看出点云Bunny和点云Dragon已经有良好的初始位置,但有些部位还有些配准偏差。

图6 点云粗配准结果

粗配准之后,通过K维树加速对应点搜索,计算出刚体变换矩阵,完成精确配准。为了保证本文方法的有效性,文献[13]与本文算法配准结果对比如图7所示。

图7 点云配准结果

从图中可以看出点云Bunny和点云Dragon得到很好的配准效果,相比初始配准一些部位出现偏差有了较大的改善。图7(b)文献[13] 配准方法也得到较好的配准效果,但兔子的耳朵和龙头部分仍存在一些偏差。

为了验证本文算法在收敛速度和配准精度方面的有效性,与传统ICP和文献[13]配准方法进行对比,结果如表1、表2和表3所示。

表1 SAC-IA算法配准结果

表3 本文算法配准与文献[13]方法对比结果

从表中可以看出,本文算法与传统ICP算法相比，配准效率提高59%,与文献[13]配准方法相比，配准效率提高22%,提高了收敛速度,同样保证了配准的精度。

经实验证明,相比传统ICP算法和文献[13]配准方法,本文算法在收敛速度和配准精度方面得到很大的改善,验证了该算法的可靠性和有效性。

5 结束语

针对传统ICP算法对点云初始位置要求高且配准效率低的问题,本文提出一种基于特征点SAC-IA算法进行粗配准,进而获得良好的初始位置,有效地解决传统ICP算法易陷入局部最优化的问题。在粗配准过程中,通过点云法向量夹角特性提取特征点并使用FPFH进行特征描述,保证了两片对云之间的对应关系。经粗配准后的点云作为ICP算法的新输入点云,同时基于K维树ICP算法加速对应点对搜索,进一步精确配准。实验结果表明本文提出的方法大幅度提高配准的效率和精度。