基于GPU的MTD性能优化

杨千禾 袁子乔 扈月松

(西安电子工程研究所 西安 710100)

0 引言

杂波抑制是雷达信号处理中一个非常重要的环节。对于固定杂波，通常会使用结构简单，运算量较低的动目标显示(Moving Target Indication,MTI)实现对杂波的抑制。不过在实际情况下，硬件工艺水平的参差不齐和雷达工作环境的复杂多样都会导致雷达目标回波出现起伏。这些现象将会影响MTI的杂波抑制效果，大部分的MTI对消器来说，其改善因子一般都被限制在20dB左右[1]，此外MTI对消器对于云杂波和雨杂波等气象杂波的无法起到有效的抑制效果。现代雷达系统通常使用动目标检测(Moving Target Detection,MTD)来克服MTI的不足，MTD通过多个带通滤波器组对雷达回波进行脉冲多普勒处理[2]，再通过对滤波器组的输出数据进行检测，以致发现目标。相对于MTI，MTD能改善滤波器的频率特性，使之更接近于最佳线性滤波，可以将改善因子提高至42dB，能够检测强杂波信号中的弱目标信号。

MTD滤波器组的实现方法一般分为两类。第一类就是设计多阶数的有限脉冲响应(Finite Impulse Response,FIR)滤波器组来对脉冲压缩之后的数据进行滤波，这种方法能针对回波信号自适应的在杂波频率处形成零陷，但是计算量过大，对于实时的信号处理系统的硬件计算能力的要求过高。另外一种方法就是用快速傅里叶变换(Fast Fourier Transform,FFT)来实现滤波器组，在计算资源有限的情况下能较好地完成MTD任务，但是需要更低副瓣的滤波器组来提升对于气象杂波的抑制性能。更低副瓣会导致主瓣的展宽更加严重，可能导致主瓣发生明显变形。

为了进一步提升雷达系统的计算能力，同时降低后续程序调试难度，实现雷达软硬件的解耦，增强雷达的可重构性。使用图形处理器(Graphics Processor Unit,GPU)代替DSP和FPGA作为雷达的计算核心，组成GPU+CPU的异构平台作为新型的雷达信号处理系统架构。在使用GPU实现雷达信号处理过程中，MTD的优化效果相较脉冲压缩(Pulse Compression,PC)和恒虚警检测(Constant False Alarm Rate,CFAR)有明显的不足，本文将着力解决这些问题并实现MTD在GPU计算平台上的进一步优化。

1 MTD的实现方法及原理

1.1 基于MTI级联FFT的MTD滤波器组

MTI的级联FFT的MTD滤波器组是在FFT之前接一个二次对消器，它可以滤去最强的地物杂波，这样就可以减少窄带滤波器组所需要的动态范围，并降低对滤波器副瓣的要求。由于DFT是一种特殊的横向滤波器，所以滤波器组的系数可以按照DFT的定义来选择，并采用快速算法FFT来实现MTD。

FFT的每点输出，相当于N点数据在这个频率上的积累，也可以说是以这个频率为中心的一个带通滤波器的输出[3]。

根据DFT的定义，N组滤波器的权值为

wnk=e-j2πk/N,n=0,1,…,N-1;k=0,1,…,N-1

(1)

式(1)中，n表示第n个抽头，k表示第k个滤波器，每一个k值决定一个独立的滤波器相应，相应地对应于一个不同的多普勒滤波器响应。因此，第k个滤波器的频率响应函数为

k=0,1,…,N-1

(2)

滤波器的幅频特性为

(3)

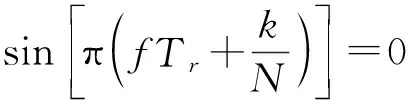
每一个滤波器都有一定的副瓣，副瓣的大小决定着杂波抑制能力的大小。为了降低副瓣，通常在计算FFT之前，一般都需要使用一个窗函数w[k]对慢时间采样数据进行加权来降低旁瓣的影响，加权之后的N点FFT可表示为

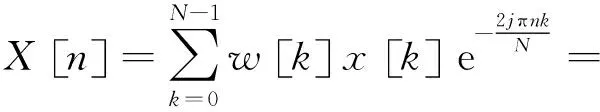
(4)

此时，第n个滤波器的幅频响应可表示为

(5)

用窗函数进行加权的主要目的是减少滤波器旁瓣的相对幅度，使信号尽量从主瓣进入，同时主瓣尽可能窄，使滤波器获得较陡的过渡带。一般来说，使用了非矩形窗对信号进行加窗之后，达成对旁瓣抑制的同时也会导致主瓣宽度地增加。主瓣电平会减少，信噪比也会相应地降低。因此要针对雷达信号体制和杂波的环境，选用合适的窗函数进行加权处理。图1为加海明窗之后的滤波器响应，可以看出在降低副瓣的同时，主瓣有所展宽。

图1 FFT滤波器组频率特性

1.2 点最佳多普勒滤波器组

采用FIR滤波器对杂波进行抑制，同时对目标信号实现相参积累，这里的处理关键在于FIR杂波抑制滤波器的设计，在设计FIR滤波器时需要根据杂波感知得到的杂波幅度、杂波谱宽来确定滤波器的凹口深浅及凹口宽度。考虑到FIR滤波器设计实时性可能无法满足的问题，通过设置默认的多种不同凹口深度和宽度的组合，提前优化设计多组FIR滤波器，使用时只需根据凹口深度和宽度选择相应的滤波器系数即可。

点最佳多普勒滤波器组只在所需的多普勒处理频段中的某一点上达到最佳，而在其他频点都是不匹配的[3]。多普勒滤波器就是用许多滤波器填满感兴趣的多普勒区域。通常实际运用中的多普勒滤波器采用N个横向滤波器填满多普勒区域，N等于处理的相干脉冲输。

点多普勒横向滤波器复数信号表示为

(6)

式(6)中A是幅度，wd是多普勒的角频率，N是相参脉冲数，Tr是雷达脉冲间的间距。信号适量则可表示为sT=(s1,s2,s3,…,sN),其中

sn=Aejwd(n-1)Trn=1,2,…,N

(7)

Rs为归一化信号协方差矩阵,Rs=E(ss*T)

(8)

归一化协方差的元素mskj为

mskl=ejwd(k-1)Te-jwi(j-1)T=ejwd(k-j)T;
k=1,2,..,n;j=1,2,…,n

(9)

式(9)中的k为行数，j为列数。

根据自适应滤波器原理，长度为N的滤波器中第k个滤波器的权适量为

wk=R-1a(fk)

(10)

式(10)中fk(k=1,2,...,N)为第k个滤波器的通带中心频率，a(fk)为导频矢量,为

a(fk)=[1,ej2πfkTr,ej2πfk2Tr,…,ej2πfk(N-1)Tr]T

(11)

R=Rc+σ2I为杂波加噪声协方差阵，RC为杂波协方差矩阵，I为单位矩阵，σ2为噪声功率[3]。R-1的作用就是使滤波器自适应地在杂波频率处形成零陷，从而抑制杂波[3]。

图2 64阶点最佳多普勒滤波器组频率特性

2 GPU并行计算的特点

2.1 CPU和GPU的功能异同

CPU和GPU是两个相互独立的处理器，有着不同的内部架构。CPU和GPU的组成如图3所示。

图3 CPU与GPU的内部结构

图3中Control是控制器、ALU为算术逻辑单元、Cache是CPU内部缓存、DRAM就是内存。可以看到GPU设计者将更多的晶体管用作执行单元，而不是像CPU结构包含大量的控制单元与缓存[5]。从实际来看，CPU芯片空间的5%是ALU，而GPU则占到了40%。物理结构上的差异导致GPU在面对大批次计算时的表现比CPU要更加优秀。

对于控制密集型的任务，特别是逻辑复杂、分支众多或深度迭代的计算任务，CPU处理效果要优于GPU；而GPU更擅长处理易于并行化的计算密集型任务。在GPU+CPU的异构计算平台中，需要根据数据特性和算法特性对一整个项目进行分解，再给CPU和GPU分配契合自身硬件特性与计算特性的任务，这样能有效提高大规模计算项目的性能。

2.2 CPU和GPU协同工作方式

GPU自身不具备独立处理进程的能力，要实现GPU的并行计算必须通过PCI-E总线与CPU相连，组成异构计算平台才能完成对任务的处理。因为一般都是由CPU向GPU传输待计算的数据并发布计算任务，所以称CPU所在位置为主机端(Host),称GPU所在位置是设备端(Device)。

程序的启动和初始化都在主机端完成，待计算数据是由CPU先处理加载到主机端内存中。在这一阶段，会完成通信端口的建立，主机内存的开辟，数据的接收/加载、组包和重排，完成数据计算前的所有准备。在主机端的准备完成之后，设备端也要在显存中(显卡的内存)中开辟相应的数据空间，完成对数据的接收准备。图4为GPU+CPU架构的基本工作原理，这种架构可以充分挥GPU的高速并行计算能力，同时兼顾CPU在逻辑运算、流程管理方面的能力，通过合理的任务分配，实现系统的高性能择优。

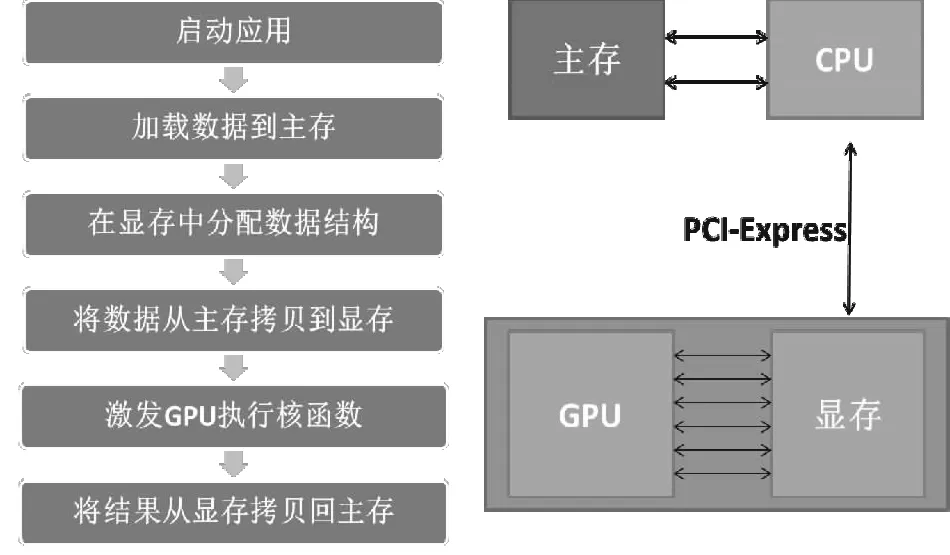
图4 CPU+GPU协同工作方式

3 MTD算法在GPU上的工程实现

在实际的计算中， R-D平面矩阵在设备的存储器中被转化成一维的向量，所有的计算都是直接针对这个一维向量进行操作。所以为了达成较好的计算性能并得到正确的计算结果，在计算前需要根据数据的存储格式和数据的读取方式来判断对是否需要对输入结果进行转置。一般情况下，PC之后的距离点数都较大，在CPU上实现矩阵转置耗费的时间较长并会占用大量的计算资源。

在GPU上实现MTD算法时，可以通过CUDA程序的函数和异构计算平台主机端与设备端分别初始化的特点，将一些步骤同时进行甚至省略，如图5所示。

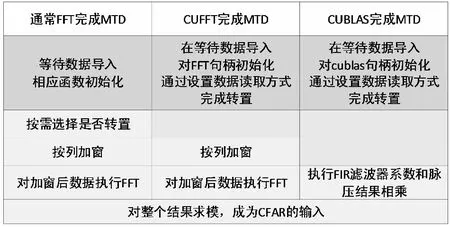
图5 基于GPU的MTD算法

图中较深阴影部分可以在整个程序的初始化或者是在主存向显存传输数据时独立完成，可以理解为HOST与DEVICE并行处理，隐藏消耗时间；图中无文字部分为省略部分，没有计算操作，并不消耗时间；浅阴影部分则是消耗计算资源的部分，也是本文优化MTD过程的重点。

3.1 加窗与求模数据读取优化

在GPU上对数据进行点乘和求模，需要使用自编的核函数来实现并行运算。GPU的计算核心在核函数内规划时是抽象成了thread,block和grid三级，thread作为最基本的计算单元包含于block中，多个thread组成的block在组成grid。在核函数中，向量的单元数据被分配给启动的thread。因为在求模和点乘的计算过程中，相邻单元直接互不影响计算结果，所以可以实现多线程并行计算。常用的多线程并行计算的情况如图6所示。

图6 常用多线程并行情况示例

相对于计算数据的规模可能无限增大，GPU的计算核心却是固定的，无法实现单个thread仅处理一个待计算单位理想情景。在数据规模较大的情况下，一个thread处理多个待计算单位时，图6的线程分配方法将会造成线程阻塞。为了避免thread阻塞，提高数据读取和计算的效率，应该使用如图7所示线程读取方式。

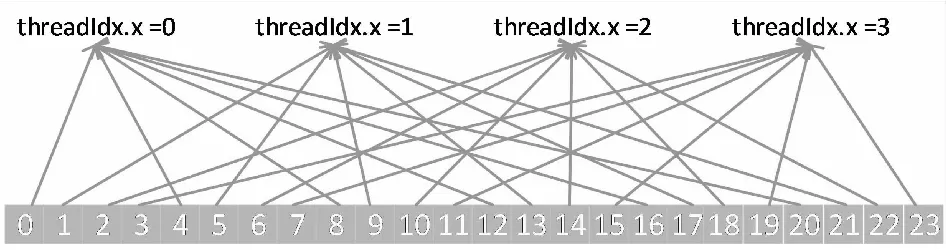
图7 防止线程堵塞的数据读取方式

3.2 使用CUFFT实现FFT

CUDA的CUFFT库函数提供了一种高效优化的快速傅里叶变换，可以用来实现MTI级联FFT的滤波器组。CUFFT的配置使用句柄(Plan)来实现，该句柄初始化定义了包括待变换信号的长度，数据类型，在内存中的存储形式等信息。使用句柄来进行初始化的方式为

cufftPlanMany(&cufftHandleplanname,
rank,n,inembed,istride,idist,
onembed,ostride,odist,CUFFT_C2C,batch)

rank表示每个进行FFT运算的信号的维度；n是一个数组，表示进行FFT的每个信号的行数，列数和页数值上一个参数rank相互呼应；inembed表示输入数据的三维点数，[页数,列数,行数]、[列数,行数]或[行数]，若数据是一维数据这个参数会被忽略；istride表示每个输入信号的相邻两个原始直接的距离；idist为两个连续输入信号的起始元素之间的间隔；onembed为输出数据的情况，同inembed；ostride和odist与此同理，最后batch为进行FFT运算的信号个数。

传输到设备端的数据都是按照列优先的存储规则来排布数据,可以通过改变参数istride与idist，或者ostride和odist来改变FFT的输入输出数据的格式，如图8所示。通过句柄初始化直接根据需求对数据进行再次排序，在初始的过程中实现矩阵转置，这一手段可以有效地优化MTD的运算时间。

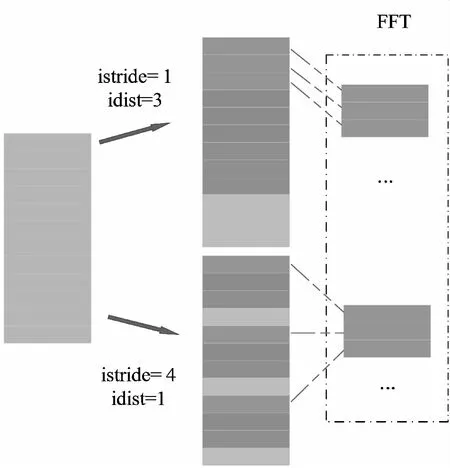
图8 FFT句柄初始化改变数据的排布格式

在完成对数据的初始化之后，调用CUFFT执行函数即可。

cufftExecC2C(planname,datain,dataout,
CUFFT_FORWARD)

其中四个函数结构分别对应之前初始化的句柄，输入输出数据的指针和FFT运算的方向。CUFFT_FORWARD是FFT运算，CUFFT_INVERSE是IFFT运算。

3.3 使用CUBLAS实现FIR滤波器组运算

在前文已经分析过，使用FIR滤波器组实现MTD能够针对不同的回波信号，使滤波器自适应地在杂波频率出形成零陷，从而灵活地抑制回波信号中的杂波。但是这种MTD算法的实现却对硬件有着巨大的压力，算法实现过程如图9所示。

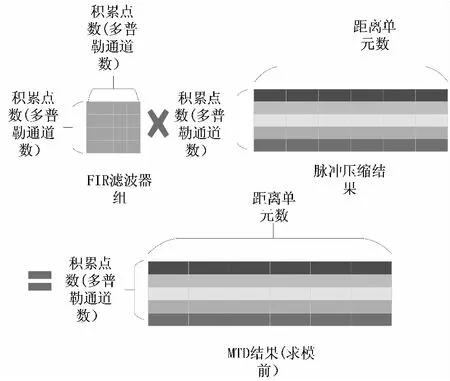
图9 FIR滤波器组实现MTD

CUBALS库对于这种规模较大的矩阵向量运算有着良好的加速效果，对于复数矩阵相乘C=alpha*A*B+beta*C有如函数

cublasCgemm(handle,transa,transb,
m,n,k,alpha,A,lda,ldb,beta,C,ldc)

transa和transb是表示矩阵A、B是否需要在计算前进行转置;m,n,k就是计算矩阵的维度信息；lda,ldb,ldc是对应矩阵的主维度。

出于整个系统兼容性的考虑，CUBLAS也选择使用列优先的存储方式。如果在计算之前对矩阵做了转置，那么矩阵的主维度就是矩阵的列数，此时的矩阵是按照C/C++以行优先的方式来存储的；反之矩阵的主维度就是行数，保持了列有限的存储方式。但是不论在计算之前是否对矩阵进行转置操作，都只是改变了矩阵数据排列格式，结果矩阵C永远都是按照列优先存储方式，因此要获得符合主机端矩阵排布的MTD结果，就需要对参与计算的矩阵进行转置，得到行优先的CT。如果后续的CFAR和杂波图计算仍然是在GPU是进行实现，则不需要此操作。表1总结了两种情况下的参数设置规则，这是使用CUBLAS库的关键。

表1 不同数据排布结果的参数选择

4 性能优化分析

4.1 两种MTD实现方案在GPU上的性能分析

在CPU+GPU异构平台上对信号处理中的MTD算法进行设计，硬件使用两块6U-VPX板卡，其中一块使用至强E5-2648L V4的14核CPU为主处理器，用于处理流程的控制和资源的调度；另一块板卡为Tesla P6 GPU，其单精度浮点计算能力为6.1Tflops，传输带宽为192 GB/s。

使用上述计算平台实现某雷达的信号处理。该雷达测试数据包含5个波束(含一个匿影波束)，积累点数为32点，有效距离单元是800(对脉冲压缩结果截取后产生)。将模拟产生的信号处理数据在GPU上运行100次之后取平均耗时，并在CPU上分别实现FFT的MTD和FIR的MTD，记录下耗费时间，所得加速比如表2所示。

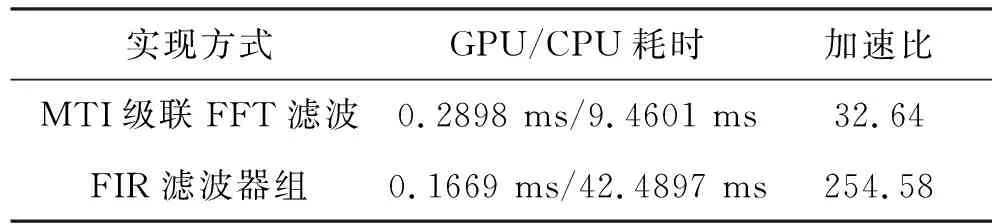
表2 MTD实现算法(开启加速选项)

将GPU计算的MTD结果导出，与经过MatLab计算的结果进行比对，MTD结果误差结果如图10所示。需要注意的是在经过2次N点FFT之后的数据比原数据扩大了N倍，对结果进行误差分析时需要将扩大的倍数考虑在内。最终求模输出的MTD结果误差在0.05%以内，考虑到在GPU上计算的数据类型为单精度(float)型，而MatLab默认的显示数据类型为双精度(double)，在进行数据转换时会对结果产生微小的影响，因此这个级别的误差基本不会影响后续的杂波图建立和恒虚警检测。

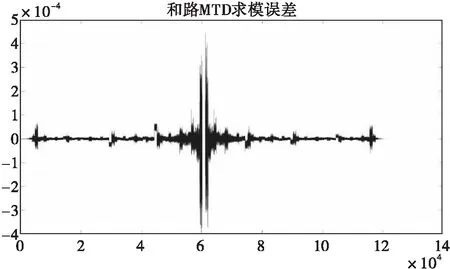
图10 MTD结果误差

可以看到使用FIR滤波器组的MTD性能要比使用FFT的MTD提升了42.4%，原本最费时的FIR滤波器组在GPU计算平台上实现了性能的超越。

GPU的结构特性利于完成大规模的矩阵运算，针对数据读取的优化与高速库函数的调用进一步提升了滤波器组的计算速度。FIR滤波器组能够让雷达系统自适应的对杂波产生抑制，增强了系统的灵活性；但是这样设计的得到的自适应的MTD滤波器会有较高的旁瓣电平，虽然不会造成主瓣的过度展宽以致主瓣变形，却会造成不同滤波器之间的目标相互影响，带来虚警。FFT的MTD对于气象杂波的抑制效果不佳，需要使用更低副瓣的滤波器组；但是加窗获得了更低的副瓣电平却造成了主瓣的进一步展宽。

不过经过优化过后的两种MTD方法耗时差异较小，经过论证分析，已在某雷达的信号处理程序中都进行了实现，根据具体情况选取更加合适的MTD方法。

4.2 使用CUBLAS实现FIR滤波的进一步优化猜想

在GPU高性能计算中，核函数与库函数的启用、初始化和计算数据的导入在整个计算过程中占据的时间花销不能忽视。所以在使用GPU进行高性能计算时，为了达到最优的计算速度，整个应用的结构和数据的传输要根据实际情况作出相对应的调整。计算数据规模的线性增加不一定导致计算时间的线性增加，所以我们将使用固定的总计算量，不同的循环次数和启动函数次数来测试MTD的计算时间。为了避免开启加速优化项对多次测试的影响，在未加速情况下计算128点积累，R-D平面总数据量为128×100000个复数的FIR滤波过程，分别才去多段计算和一批次计算的方法，测试时间如表3所示。

表3 各种情况下的FIR滤波器组计算时间(未开启加速选项)

从得出结果的后三项可以看出，并不是每次计算的矩阵维度小就一定能节省每次的运算时间，单次函数启动和数据导入的开销据决定着要选则合适的数据维度才能达到最好的计算优化；其次每次计算的数据维度越大，在计算的总耗时上就会有提升。所以在信号处理过程中，在不造成系统其它分系统阻塞或者使计算资源发生空闲的情况下，尽量在GPU计算前堆积足够大量的数据，单次直接计算大量数据，减少函数启动的次数，优化整体计算的时间。

5 结束语

本文从实现MTD的两种方法入手，分析了FIR滤波器组和FFT计算实现MTD的优缺点。针对在较大数据情况下，使用FIR滤波器组实现MTD会导致计算资源的紧张和影响系统实时性的问题，提出了使用CPU+GPU异构架构来完成计算过程优化的方式。结果表明在GPU上实现MTD算法的处理结果与在CPU上所得结果误差在0.05%内。经过算法优化和GPU加速选项优化之后，MTI级联FFT的滤波器组在GPU上的计算效率相比在CPU上的串行计算提高了近32.64倍，而本身以运算量较大的FIR滤波器组算法相比CPU提高了近254.58倍。

FIR滤波器组能够实现自适应的杂波抑制，增加了系统的灵活性，但副瓣较高；FFT滤波器组具有更低的副瓣电平，却因为加窗抑制电平造成主瓣的进一步展宽。在经过优化之后，两种MTD在GPU上的计算耗时来到了同一个水平。所以在以GPU为核心的雷达信号处理平台中，可以根据具体需求择优选择两种MTD实现方法。最后对于CUBALS库在雷达信号处理过程中的进一步优化，提出了单次计算大量数据，减少函数启动次数的建议。