一种改进型海尖峰背景下的目标检测算法

宋 锐

(西安导航技术研究所 西安 710068)

0 引言

海尖峰是一种离散、高幅值、极化特性强、类似小目标的海杂波[1]，因此海尖峰的存在不利于目标的分离和提取。当高分辨率雷达以低擦地角照射粗糙海面时，其雷达回波强度会明显增强，相应的大杂波幅度值出现的概率增加，杂波幅度的概率密度函数(PDF)曲线就会表现出较长的“拖尾”效应，这种效应也被称为雷达的海杂波尖峰(Spike)效应[2-5]。但在新的测量和试验中发现，即使是低分辨率雷达也可能会形成海尖峰。

由于海杂波的谱宽较宽，动目标显示(MTI)、自适应运动杂波抑制(AMTI)、动目标检测(MTD)等传统的滤波方法不能很好地将海杂波滤除干净，尤其是与运动目标特性相似的海尖峰，因此，抑制海杂波的同时保留真实目标成为热点难点问题。研究者们通过建立海杂波模型[6-8]模拟复杂多变的海杂波特性分布，进而研究海杂波抑制方法，寻求一种通用、高效的海杂波抑制方法成为海杂波抑制算法研究的主流趋势。文献[9]和文献[10]采用隔周测频的方法计算瞬时多普勒频率，提出了利用多普勒频率相关性判别抑制海杂波的海杂波抑制方法。文献[9]提出基于多普勒频率相关性检测的海杂波抑制方法，对连续几个脉冲的多普勒频率进行相关性检测，利用门限判别抑制海杂波保留所需的目标信息，但这一方法存在不足之处，若海杂波在某一区域多普勒频率相关性也较强，就可能将海杂波当做目标，从而造成虚警。文献[10]在文献[9]的基础上增加了一级判别方法，提出了两级多普勒频率相关性判别方法，虽相比于文献[9]可减少一定的误判，但是对于第二级判别方法所利用的拟主瓣过于经验化，拟主瓣的长度完全是凭借经验来判断，不具有通用性，这种方法也存在可能将相关性较强的海杂波当做目标的情况发生。文献[11]主要是对实测海杂波数据进行海杂波特征提取，利用16点FFT以及固定门限得到多普勒平面，通过多帧的海杂波波动的标准差以及相对多普勒速度对海面低空飞行目标和假目标进行特征提取和特征分类，从而实现海杂波的特征提取。

本文根据海尖峰与运动目标在连续距离单元和连续脉冲构成的距离-方位二维区域中多普勒频率变化程度存在差异的思想，对文献[9]和文献[10]加以改进，提出了一种改进型的海尖峰背景下的目标检测算法。利用隔周测频[12]的方法对传统滤波后的海杂波数据计算连续几个脉冲的瞬时多普勒频率，得到距离-方位二维的多普勒频率信息，根据海杂波多普勒频率具有跳变的特性[13]，利用距离-方位二维联合多普勒频率稳定度表示连续距离单元和连续脉冲构成的距离-方位二维区域中多普勒频率的变化程度，通过门限判别保留多普勒频率稳定的目标区域，剔除多普勒频率变化较大的海尖峰区域，从而实现了海尖峰背景下的目标检测。该算法没有固定的海杂波模型限制，通过实测数据验证了该算法能够较好地抑制海尖峰，减少由于海尖峰造成的虚警，实现海尖峰背景下的目标检测。

1 改进型海尖峰背景下的目标检测算法

1.1 瞬时多普勒频率计算方法

本文利用等T的海杂波数据，采用隔周测频的方法计算瞬时多普勒频率，具体原理如下：

设雷达回波信号为u(t)=s(t)+c(t)+n(t)，其中s(t)为目标回波信号，c(t)为杂波，n(t)为加性噪声。以目标为线性调频信号为例，脉压后的目标回波信号为s(t)=A(t)ej((2aπfd+b)t+φ0)，其中A(t)为幅值，a和b均为常数，fd为目标信号的多普勒频率，φ0为初相。杂波可表示为c(t)=B(t)ej(2πfd1t+φ0)，其中B(t)为杂波的幅值，fd1为杂波的谱中心，φ0为初相。由于噪声与杂波和信号均不相关，且不同PRT之间噪声也互不相关，因此计算u(t)的自相关函数时与噪声n(t)无关，那么由以下两种较为极端的情况对其原理进行说明。

情况一：假定雷达回波信号中只有杂波和噪声无目标，那么u(t)=c(t)+n(t)，则u(t)的自相关函数为

R(Tr)=E[u(t)u*(t-Tr)]=E[B(t)B(t-Tr)]ej2πfd1Tr

(1)

式(1)中Tr为脉冲重复周期，由于B(t)为窄带信号，于是B(t)≈B(t-Tr)，则E[B(t)B(t-Tr)]=E(B(t)2)是一个实数。因此得到隔周测频的多普勒频率计算公式为

(2)

用时间平均代替统计平均可以得到u(t)自相关函数的估计值为

(3)

其中N为u(t)的采样序列长度，N的取值与波束宽度有关。从而得到实际应用的隔周测频的多普勒频率计算公式为

(4)

情况二：同理若无杂波或杂波可以忽略不计时，雷达回波信号只由目标和噪声构成，则u(t)=s(t)+n(t)，那么u(t)的自相关函数如式(5)所示。

R(Tr)=E[u(t)u*(t-Tr)]=
E[A(t)A(t-Tr)]ej(2aπfd+b)Tr

(5)

由于目标信号的幅值也存在着A(t)≈A(t-Tr)，则E[A(t)A(t-Tr)]=E(A(t)2)是一个实数，那么可代入公式(2)中得到

(6)

同样通过时间平均代替统计平均，通过公式(4)得到实际应用的目标区域隔周测频的结果为

(7)

通过情况一和情况二两种极端情况可以看出，利用隔周测频公式所计算的杂波的多普勒频率值是杂波的真实多普勒频率值，因此杂波区所计算的多普勒频率稳定性较差，而利用其计算的目标的多普勒频率值虽不是目标真实的多普勒频率值，但也由目标多普勒频率经过固定变换后得到的值，因此目标区所计算的多普勒频率值稳定性较好。通过分析可以看出，只要不是被杂波淹没的目标区域，这种瞬时多普勒频率计算方法就可考虑应用于区分目标区域和海尖峰区域的算法当中。

1.2 距离维多普勒频率稳定度判别

对于距离-方位二维雷达回波信号，由于雷达散射截面积(RCS)导致目标存在于连续距离单元中，那么在目标区域中同一脉冲连续距离单元的信号多普勒频率具有相似性，这种信号多普勒频率在距离维上的关联特性可以利用距离维多普勒频率稳定度来度量。距离维多普勒频率稳定度是由方位维多普勒频率相关性和距离维多普勒频率方差描述的，其中方位维多普勒频率相关性是通过相邻脉冲连续距离单元的多普勒频率序列的相关系数表征的，而距离维多普勒频率方差则是对用于做相关的多普勒频率序列频率波动程度的反应。

设第j个脉冲的连续距离单元的多普勒频率为f1j,f2j,…,fij，其中fij是利用第i个距离单元的第j个脉冲到第j+N个脉冲计算的多普勒频率值，N为计算多普勒频率的脉冲序列长度。对于m个距离单元长度的相邻脉冲间的信号的多普勒频率序列求相关系数为

(8)

其中Xij=[fij,f(i+1)j,…,f(i+m-1)j]，Xi(j+1)=[fi(j+1),f(i+1)(j+1),…,f(i+m-1)(j+1)]为相邻脉冲的第i个距离单元到第i+m-1个距离单元的多普勒频率序列，由多次试验表明距离单元长度m与距离分辨力、目标RCS等有关。Cov(Xij,Xi(j+1))为相邻脉冲的多普勒频率序列的协方差，D(Xij)、D(Xi(j+1))表示这两个多普勒频率序列的方差，同时D(Xij)、D(Xi(j+1))作为两个序列的方差也是多普勒频率稳定度判别的一个判别因素，而方差门限的选择与信噪比、海况等都有关系。

通过对距离-方位二维雷达回波信号的多普勒频率数据滑动处理，可以求得全部距离-方位二维数据的多普勒频率的相关系数，当然也可以只计算感兴趣的区域，通过相关系数门限初步判断是否为目标，再对做相关的两个序列分别计算方差并对两个方差进行选大，选大后与方差门限进行对比，进一步通过方差门限进行筛选。当某点的相关系数大于相关系数判决门限同时其方差小于方差判别门限时，认为其所对应的多普勒频率序列为目标的多普勒频率序列，保留相应的多普勒频率值，反之，认为是海杂波的多普勒频率序列同时将对应的多普勒频率值置零。

1.3 方位维多普勒频率稳定度判别

对于距离-方位二维雷达回波信号，目标速度不会在几微秒的时间发生突变，因此目标区域中同一距离单元连续脉冲信号的多普勒频率具有相似性，这种信号多普勒频率在方位维的关联特性可以利用方位维多普勒频率稳定度来度量。方位维多普勒频率稳定度是由距离维多普勒频率相关性和方位维多普勒频率方差描述的，其中距离维多普勒频率相关性是通过相邻距离单元连续脉冲的多普勒频率序列的相关系数表征的，而方位维多普勒频率方差则是对用于做相关的多普勒频率序列频率波动程度的反应。

设第i个距离单元连续脉冲的多普勒频率为fi1,fi2,…,fij，其中fij是利用第i个距离单元的第j个脉冲到第j+N个脉冲计算的多普勒频率值，N为计算多普勒频率的脉冲序列长度。对于k个脉冲长度的相邻距离单元间的信号的多普勒频率序列求相关系数为

(9)

其中Xij=[fij,fi(j+1),…,fi(j+k-1)]，X(i+1)j=[f(i+1)j,f(i+1)(j+1),…,f(i+1)(j+k-1)]为相邻距离单元的第j个脉冲到第j+k-1个脉冲的多普勒频率序列，由多次试验表明脉冲长度k一般取5～7。Cov(Xij,X(i+1)j)为相邻距离单元的多普勒频率序列的协方差，D(Xij)、D(X(i+1)j)表示这两个多普勒频率序列的方差，同时D(Xij)、D(X(i+1)j)作为两个序列的方差也是多普勒频率稳定度判别的一个判别因素，而方差门限的选择与信噪比、海况等都有关系。

通过对距离-方位二维雷达回波信号的多普勒频率数据滑动处理，可以求得全部距离-方位二维数据的多普勒频率的相关系数，当然也可以只计算感兴趣的区域，通过相关系数门限初步判断是否为目标，再对做相关的两个序列分别计算方差并对两个方差进行选大，选大后与方差门限进行对比，进一步通过方差门限进行筛选。当某点的相关系数大于相关系数判决门限同时其方差小于方差判别门限时，认为其所对应的多普勒频率序列为目标的多普勒频率序列，保留相应的多普勒频率值，反之，认为是海杂波的多普勒频率序列同时将对应的多普勒频率值置零。

1.4 距离-方位二维联合多普勒频率稳定度判别实现海尖峰背景下的目标检测

距离-方位二维联合多普勒频率稳定度判别包括距离维多普勒频率稳定度判别和方位维多普勒频率稳定度判别，图1为算法的流程图，算法步骤如下：

图1 距离-方位多普勒频率稳定度判别算法流程图

1)利用隔周测频的方法计算输入信号矩阵的瞬时多普勒频率，得到多普勒频率矩阵。

2)利用距离维多普勒频率稳定度判别方法，将满足条件的多普勒频率值赋给相同维度零矩阵对应位置。

3)利用方位维多普勒频率稳定度判别方法，将满足条件的多普勒频率值赋给相同维度零矩阵对应位置。

4)对两个多普勒频率矩阵进行融合，保留两个矩阵中均不为0的多普勒频率值，得到融合后的多普勒频率矩阵。

5)将融合后的多普勒频率矩阵中多普勒频率值不为0所对应的信号数据保留原值，其余归一化成噪声电平。

2 实测数据处理结果及分析

本文使用的实测海杂波数据为某远程预警雷达在远程机扫模式下测得的低掠海角回波信号。该雷达发射的为线性调频脉冲信号，经海面和目标的散射后脉冲信号被雷达接收，将所接收到的回波信号经过方位维重排后得到距离-方位二维回波信号。由于实验雷达波束宽度0.9°，机扫方式下一个波束内共7个连续脉冲，因此利用隔周测频计算多普勒频率所用的采样序列长度N可以取4～6，这里以N=5为例进行仿真说明。本组实验中利用实际采集的某一组海杂波数据进行仿真说明，在数据中人为加入了两个模拟的目标。如图2所示为该实测海杂波数据经过传统滤波后的海杂波数据，有两个目标和一个海尖峰。

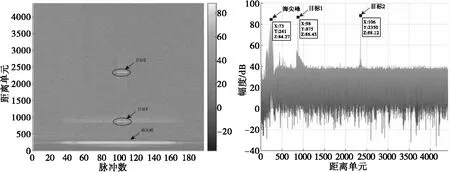
图2 传统滤波后的全部PRT海杂波数据

本文采用利用隔周测频的方法计算瞬时多普勒频率，表1和表2分别为利用隔周测频测得的目标区域和海尖峰区域的多普勒频率值，通过分析可以发现目标区域所测的多普勒频率值稳定度很高，多普勒频率值变化不大，而海尖峰区域所测的多普勒频率值跳变很大。

表1 隔周测频计算的目标区域多普勒频率值

表2 隔周测频计算的海尖峰区域多普勒频率值

对数据的距离-方位二维多普勒频率信息计算距离维多普勒频率相关系数和方位维多普勒频率相关系数，表3为目标区域和海尖峰区域的距离维多普勒频率相关系数对比，通过表格看出目标区域的相关系数大都在0.99999以上，海尖峰的距离维多普勒频率相关系数也很高，虽然没有目标区域的相关系数高，但是也可能存在误判的情况发生。表4为目标区域和海尖峰区域的方位维多普勒频率相关系数对比，可以看出目标区域的方位维多普勒频率相关系数比较稳定，均在0.9以上，而海尖峰区域的方位维多普勒频率相关系数不稳定，虽然基本上其区域的相关系数整体较弱，但也存在多普勒频率相关系数较大的情况。通过表3和表4可以看出，只凭借多普勒频率相关性判别区分海尖峰区域和目标区域是不完善的，为了减少将多普勒频率相关系数高的海杂波当作信号的情况发生引入了方差判别。

表3 距离维多普勒频率相关系数

表4 方位维多普勒频率相关系数

通过分析表1和表2可以看出，目标的距离-方位二维区域的多普勒频率比较稳定，那么方差较小，而海尖峰的距离-方位二维区域的多普勒频率通常稳定性较差，则方差较大，利用这一特性，对做相关的多普勒频率序列计算方差，进一步筛选目标。通常海尖峰即使某一维的多普勒频率方差较小，也无法使多普勒频率相关系数和多普勒频率方差同时满足门限要求，因此可以通过多普勒频率稳定度来对目标和海尖峰进行判别。

如果只是距离-方位二维联合多普勒频率相关性判别，可能存在海杂波抑制的同时目标也有一定的缺失或者目标完整但海杂波抑制不彻底的情况发生，通过表3和表4可以看到，海尖峰也存在多普勒频率相关系数较高的情况。因此同样达到抑制海杂波保留真实目标这一目的，相比多普勒频率稳定度判别，多普勒频率相关性判别会抬高相关性判别的门限值，还会存在海尖峰误判的情况，适用性没有多普勒频率稳定度好。如图3所示为距离-方位二维联合多普勒频率相关性判别后的海杂波数据，存在即使目标信息缺失海杂波依然抑制不干净的现象。当然在多普勒频率稳定度判别时，很容易想到只用多普勒频率方差判别是否可行，通过实验表明如果只是距离-方位二维联合多普勒频率方差判别，在信噪比相对较低时利用隔周测频得到的瞬时多普勒频率波动可能较大，方差门限的选取可能很大，不足以抑制海杂波，在信噪比较高时即使方差门限选取相对合适但是由于没有相关性的检测，会造成一些多普勒频率波动较小的海杂波误认为目标的情况发生，因此多普勒频率相关性判别和方差判别相辅相成，如图4所示为利用距离-方位二维联合多普勒频率方差判别后的海杂波数据，存在抑制不掉的海杂波、海尖峰。

图3 距离-方位二维联合多普勒频率相关性判别后的全部PRT海杂波数据

图4 距离-方位二维联合多普勒频率方差判别后的全部PRT海杂波数据

通过距离维多普勒频率稳定度判别后的数据如图5(a)所示，通过方位维多普勒频率稳定度判别后的数据如图5(b)所示，通过距离-方位二维联合多普勒频率稳定度判别后的数据如图6所示，可以看出如果只是距离维多普勒频率稳定度判别或者只是方位维多普勒频率稳定度判别可能会存在海尖峰和海杂波不完全抑制的情况，但是距离-方位二维联合判别会明显减少了海尖峰和海杂波抑制不彻底的情况，由此可见本文的改进型海尖峰背景下的目标检测算法是有效的。

图5 某一维多普勒频率稳定度判别后的全部PRT海杂波数据

图6 距离-方位二维联合多普勒频率稳定度判别后的全部PRT海杂波数据

3 结束语

本文提出了一种改进型海尖峰背景下的目标检测算法，利用隔周测频方法计算瞬时多普勒频率，根据目标区域和海尖峰区域多普勒频率稳定度的差异，通过多普勒频率相关性和多普勒频率方差表征其多普勒频率稳定度，通过距离维多普勒频率稳定度判别和方位维多普勒频率稳定度判别，即距离-方位二维联合多普勒频率稳定度判别方法，达到抑制海尖峰保留真实目标的目的。该方法虽有一定的适用条件，但没有海杂波具体模型的限制，具有一定的通用性，海尖峰抑制效果明显，有效地降低了虚警。由于方法原理限制，这一方法存在一定的局限性，对信杂噪比要求较高，适用于海尖峰背景下的目标检测，因此需要初步滤波后再应用此算法进行目标检测。