基于高斯插值提高雷达测距精度的研究

马 兰 李照照 杨雪林 井 伟 路鲲鹏

(1. 西安电子工程研究所 西安 710100； 2. 中国兵器工业试验测试研究院 渭南 714200；3. 陆军驻西安地区第六军代室 西安 710100)

0 引言

测距精度一直是研究雷达技术的重要内容之一。通常情况下，雷达测量目标距离的方法是对目标回波作脉压处理后，根据得到的功率谱曲线，找到最大值点对应的距离单元号来确定目标距离。但受到采样率的约束，在脉压波形内采样得到的最大值点与真实脉压波形的峰值点之间存在一定的误差，也就是二者对应的采样时间之间存在一定的偏差，因此雷达处理分辨率有限导致了不可避免的测距误差，降低了测距精度，所以研究减小距离量化误差的方法是研究雷达测距技术的一项重要内容。

文献[1]主要介绍了一种对回波主瓣面积作梯形近似来插值估计出真实峰值的方法。首先从回波波形的特点入手，对回波信号中的目标区域进行细化，在固定的采样间隔之间仅做一次插值处理，等效于降低目标回波区域内的采样间隔，在雷达各参数都固定的情况下有效提高测量精度，但采用这种方法时测距精度会明显受到噪声的影响，在有噪声时测量误差会急剧增加[1]。文献[2]介绍的方法是先用FFT得到差频信号极大值和次大值的谱线位置，再根据谱峰极大值估计方法计算出真实极大值的谱线位置，从而实现测距系统的高精度估计，但是该方法计算量较大[2]。文献[3]是将高斯插值法应用于相邻的前后三个导频子信道，根据它们之间的相关性来估计数据子载波信道响应。相比于线性插值算法，高斯插值算法虽然精度更高，但计算复杂度会随着多项式阶数的增加而增加[3]。

本文针对LFM信号加入高斯白噪声作脉冲压缩得到的脉压波形，结合先验信息，当窗函数选定时，脉压结果主瓣内的波形可近似为高斯分布，通过利用高斯插值算法来预估脉压波形真实峰值出现的位置，实现了减小距离量化误差，提高雷达测距精度的目的。

1 雷达测距量化误差的产生

在雷达测距过程中，影响距离跟踪精度的因素主要包括以下几个方面：热噪声[4]、多路径、大气传播误差、距离量化误差、目标闪烁以及定时脉冲抖动[5]。本次研究主要针对减小距离量化误差来提高雷达测距精度[6-7]。

脉冲法雷达测距的一般公式为

(1)

式(1)中：c为电磁波传播速度(在自由空间传播时约等于光速)；tR为回波相对于发射信号的延迟。

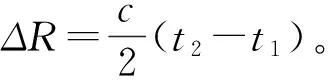
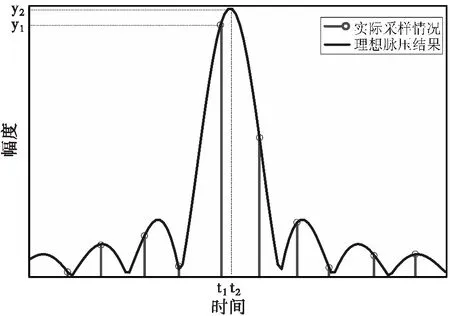
图1 雷达测距量化误差的产生

2 高斯插值算法的基本原理

2.1 高斯插值算法

如图2所示，高斯插值算法是结合先验信息，将回波脉压结果主瓣内的波形近似为高斯分布，利用脉压结果中采样点的幅度最大值及最大值对应距离单元左、右两个单元中的次大值进行插值运算处理。设高斯分布的概率密度函数为

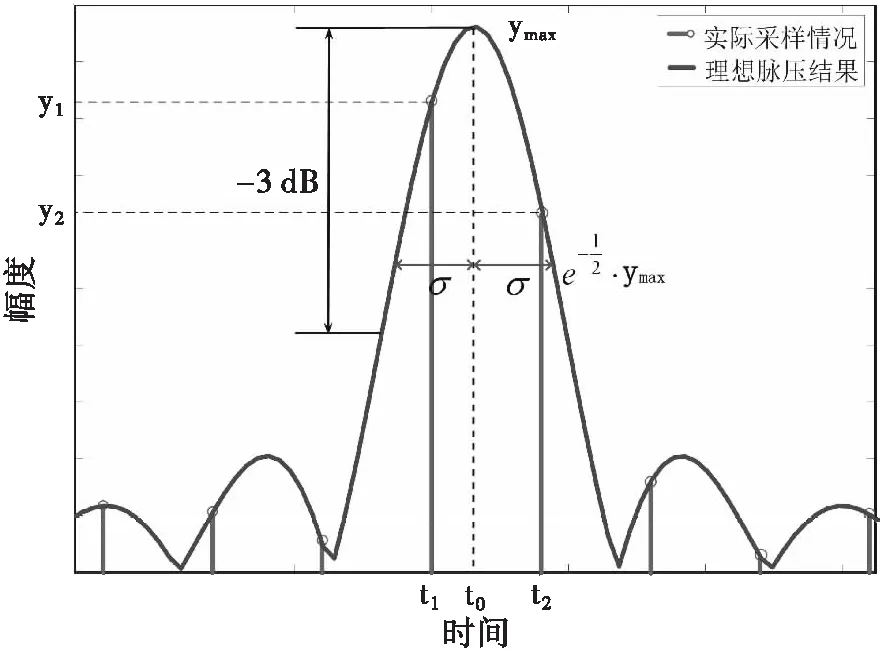
图2 高斯插值算法原理分析

(2)

其中，t0表示高斯分布的均值，σ2表示高斯分布的方差。

在目标回波信号的脉压结果中，设采样点幅度最大值和次大值分别为y1和y2，对应的采样时间分别为t1和t2，根据高斯分布的概率密度函数可以得到方程组(3)。

(3)

根据方程组(3)得到

(4)

对式(4)两边同时取对数得

(lny1-lny2)·2σ2=t22-t12+2t0(t1-t2)

(5)

得到t0的表达式为

(6)

其中，t0即为回波脉压结果的真实峰值出现的时间。

式(6)中，高斯分布的方差σ2未知，所以必须结合先验信息将σ2表示出来。

2.2 高斯分布的方差估计

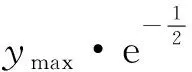
假设雷达仿真参数如表1所示，将较高采样率下的脉压波形作为参考波形，此时的脉压波形几乎是连续的，通过仿真将主瓣内的脉压波形近似为高斯分布，可以得到高斯分布概率密度函数。

表1 仿真参数设计

根据表1中的仿真参数设计，得到如图3所示的信号脉压结果，为了保证在主瓣内所选时间区间中至少能得到两个采样点，将采样时间区间长度选为两个采样时间间隔，对应到图3中应为[9.2 μs,10 μs]。

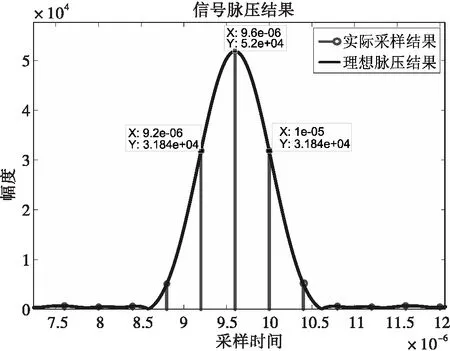
图3 不同采样率下的信号脉压结果

首先，直接用脉压结果数据拟合高斯分布函数。如图4所示，为了方便计算，在选取的采样时间区间上将脉压波形的横坐标归一化为采样时间单元，其中一个采样时间单元表示实际采样结果中相邻两个采样点之间的采样时间间隔与真实采样率的乘积。根据图4中所选主瓣区间的信号脉压结果数据，将采样时间单元和脉压波形幅度分别作为横纵坐标拟合高斯分布函数。

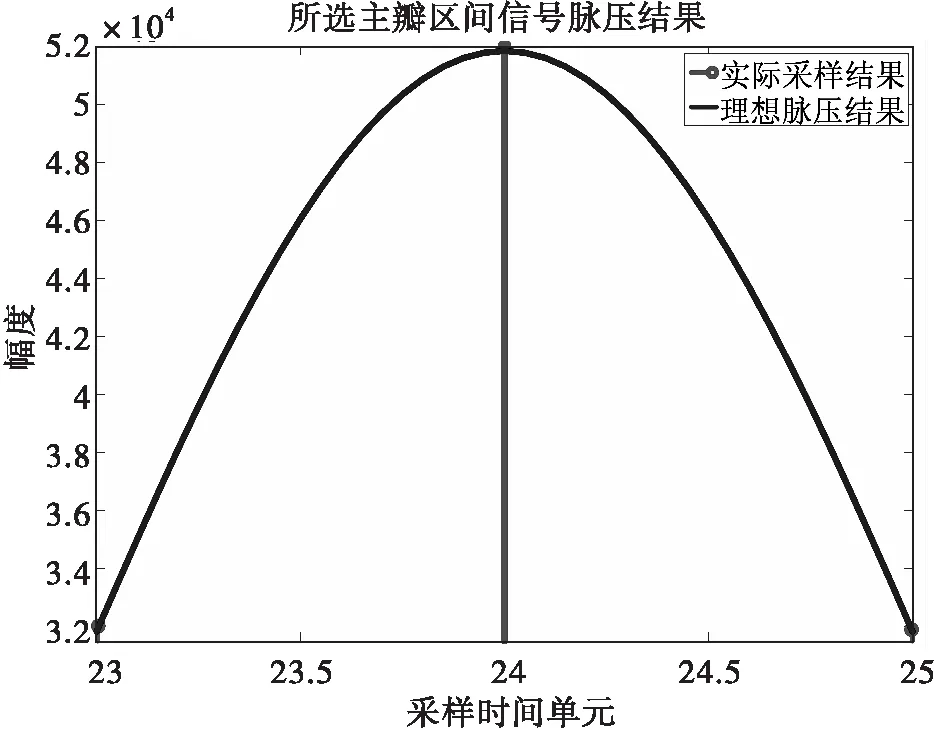
图4 所选主瓣区间的信号脉压结果

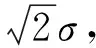
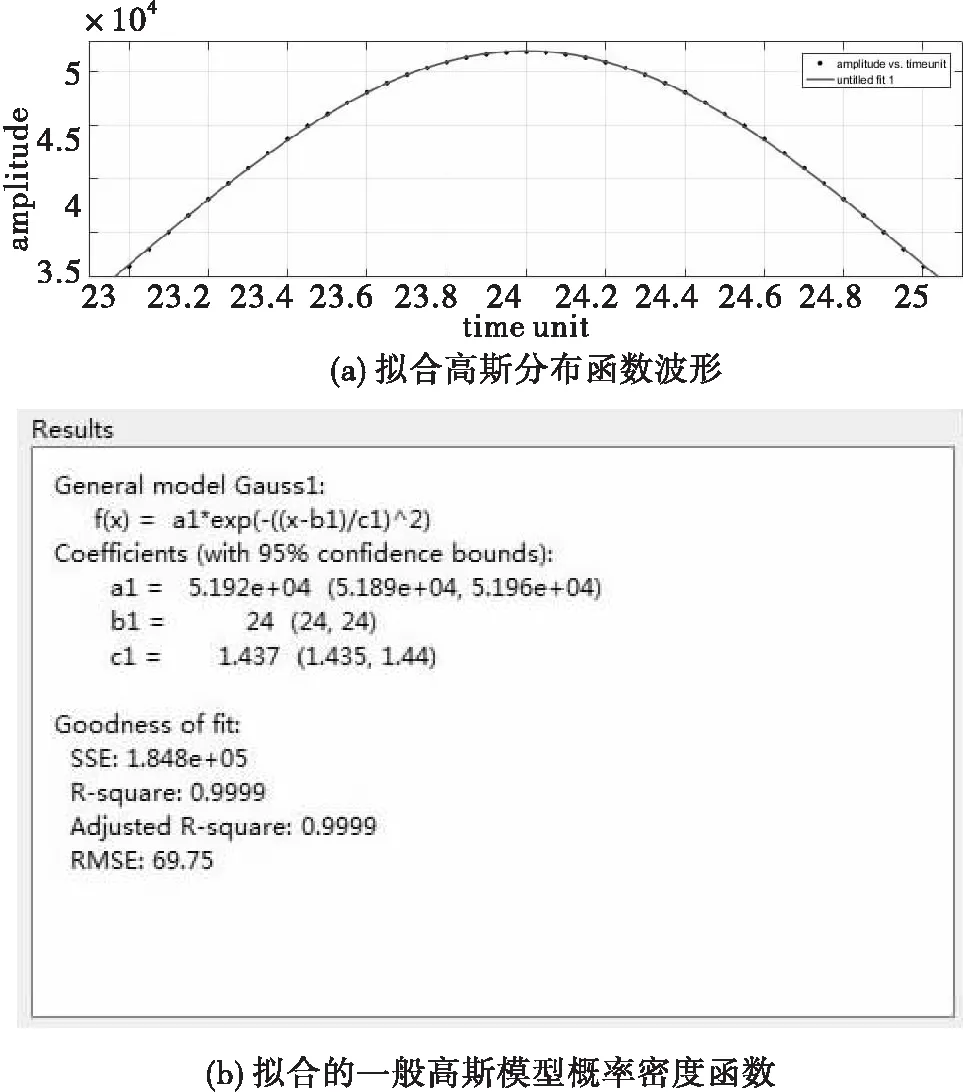
图5 所选脉压波形主瓣区间拟合的高斯分布结果分析

为了确定拟合高斯分布函数的方差是否会由于脉压结果的归一化而发生变化，对图4中所选主瓣区间的脉压结果幅值作归一化处理，如图6所示，将采样时间单元和归一化幅度分别作为横纵坐标拟合高斯分布函数。

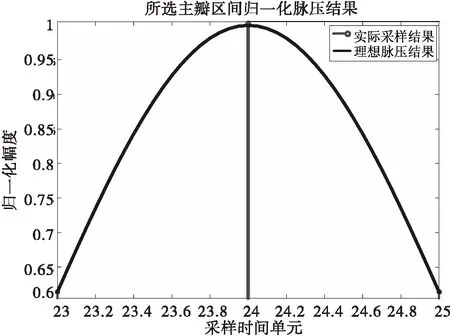
图6 所选主瓣区间的归一化脉压结果

由以上仿真结果可以看出，对回波脉压结果作归一化处理后再拟合高斯分布函数，与直接用脉压结果数据拟合的高斯分布函数的均值和方差是一致的，只是拟合高斯分布函数的峰值会与归一化同时变化。

因此，在雷达实际工作中，当时宽、带宽确定且窗函数选定时，结合先验信息将主瓣内的脉压波形近似为高斯分布时，高斯分布函数的方差为一固定值，且该值可以在较高的采样率下通过仿真得到。

3 算法验证

根据表1中的仿真参数设计，假设回波脉压波形不动，即脉压波形峰值出现的采样位置不变，将实际采样率下的采样最大值和次大值在所选主瓣波形对应的时间区间[9.2 μs,10 μs]内进行移动，使各种情况下的采样最大值和次大值位置分布都被考虑到，如图8所示。

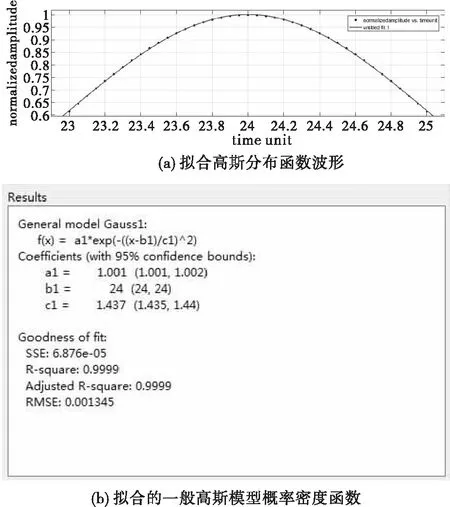
图7 所选归一化脉压波形主瓣区间拟合的高斯分布结果分析

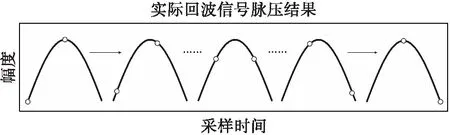
图8 实际脉压结果采样最大值和次大值位置分析

假设每次移动0.02 μs，则在采样时间区间[9.2 μs,10 μs]内采样最大值和次大值位置分布共有21种情况，将各种情况下的采样最大值和次大值数据统计参见表2所示。

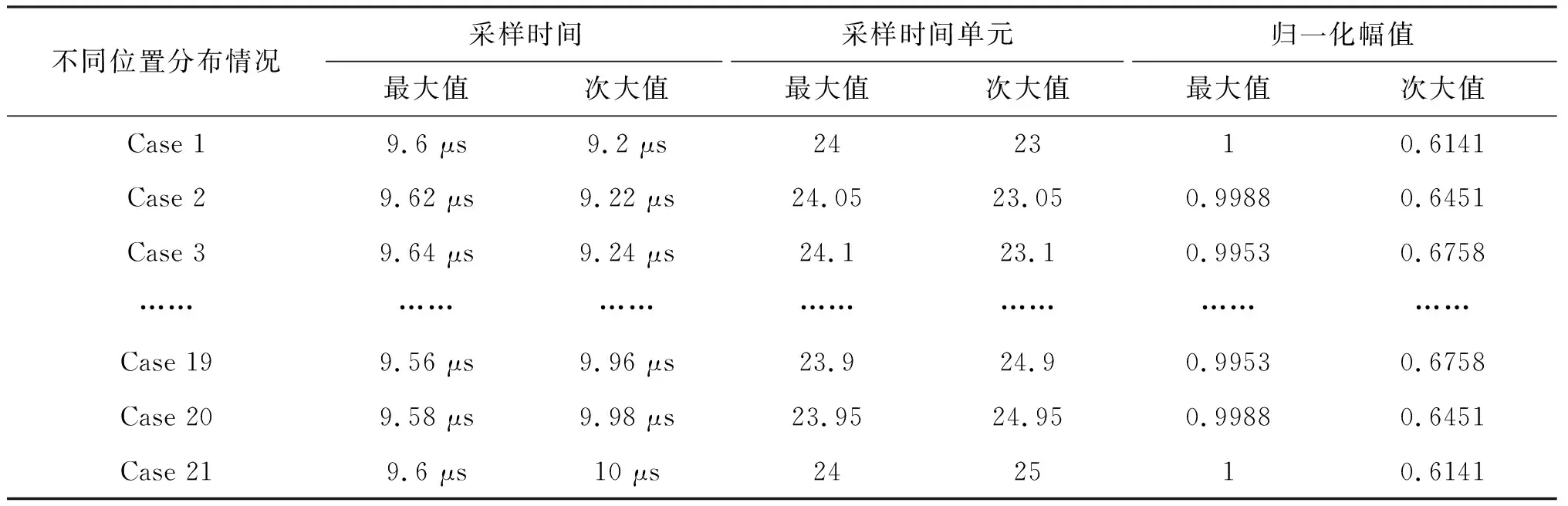
表2 信号脉压结果归一化数据

根据高斯插值算法的原理，结合式(6)，对以上21种采样最大值和次大值分布情况进行插值处理来估计拟合高斯分布函数的均值，由均值的估计量可以得到回波脉压波形峰值时间的估计量。由图8可知，由于回波脉压波形不动，故回波峰值时间也是不变的，对应仿真中选取的时间区间，回波峰值出现的采样时间单元为24，采样时间为9.6 μs。

根据图9的仿真结果可以看出，在未加噪声的情况下，对回波信号脉压结果采样最大值和次大值出现的不同位置，用高斯插值算法估计回波脉压结果的峰值时间，其精度较高，几乎没有误差。以上仿真分析验证了高斯插值算法的有效性。

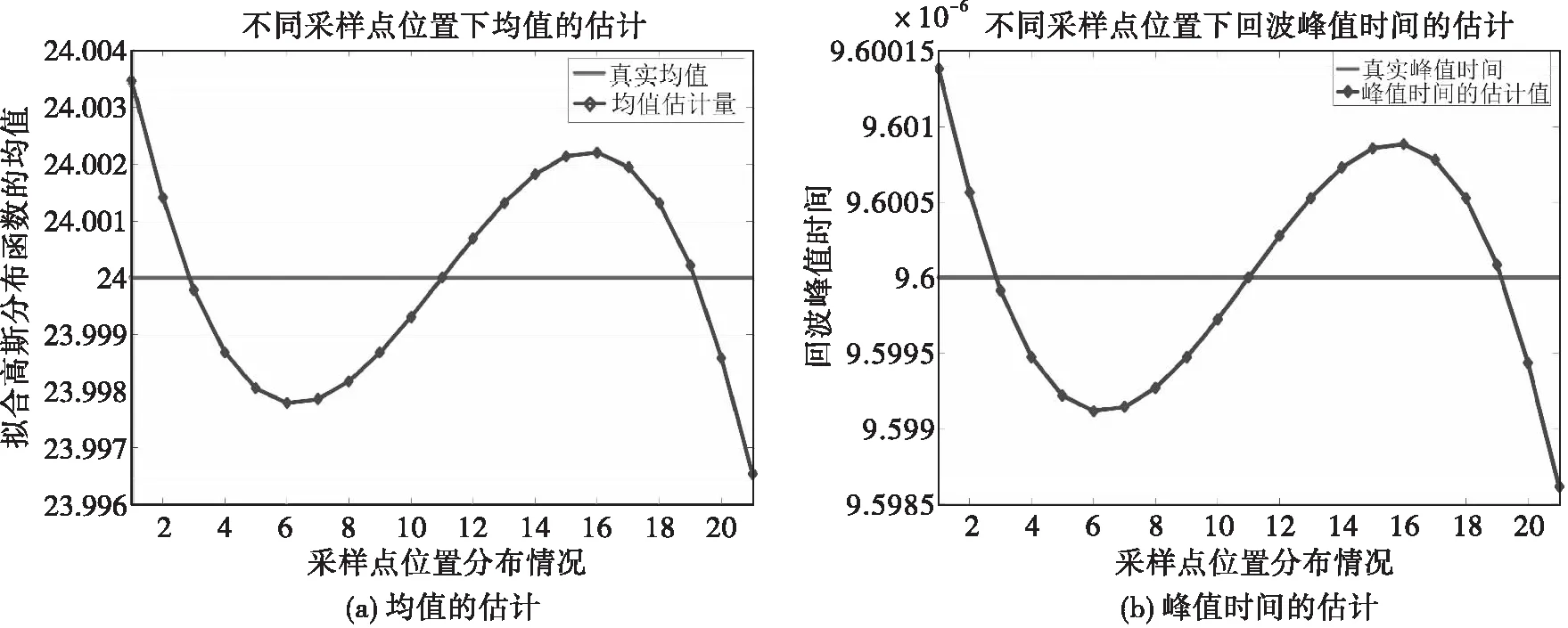
图9 不同采样位置下均值和峰值时间的估计分析

下面加入噪声分析经过插值处理后距离量化误差的变化。假设雷达仿真参数如表1所示，SNR的变化范围取10～30 dB。

如图10所示，仿真中相邻两个采样点间隔为0.4 μs，针对回波脉压结果主瓣内采样最大值和次大值位置出现的不同情况，故选择以上四种位置分布分别进行仿真分析，其中，图10(b)和图10(d)的采样点位置分布关于脉压波形对称。

用高斯插值算法对以上各种情况进行插值处理，并将插值结果转换为距离量化误差。

从图11可以看出，对采样最大值和次大值在脉压波形上出现的不同位置作高斯插值处理，得到的插值结果与真实峰值时间吻合度较高，最终的距离量化误差最大值仅有13.2 m。以上仿真结果表明，高斯插值算法在充分利用先验信息的基础上，显著提高了雷达测距精度。同时注意到，当采样最大值与次大值的幅度几乎一致时，如图10(c)所示，真实峰值时间即为两个采样点中心位置所处的采样时间，此时可以不作插值处理，直接用两个采样时间的中心值作为峰值时间来计算距离，可以进一步减小测距误差。

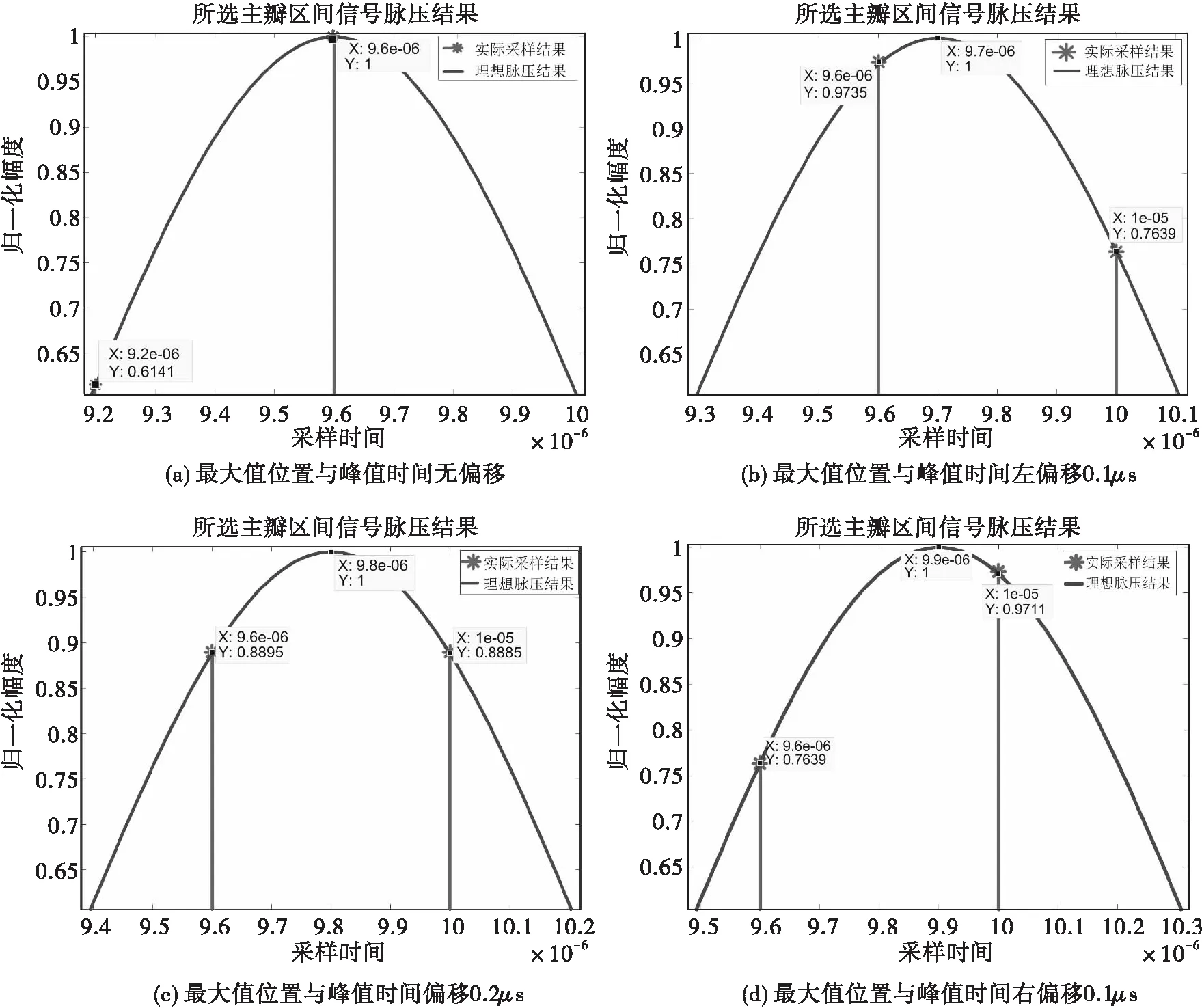
图10 采样最大值位置与峰值时间的不同偏移情况分析

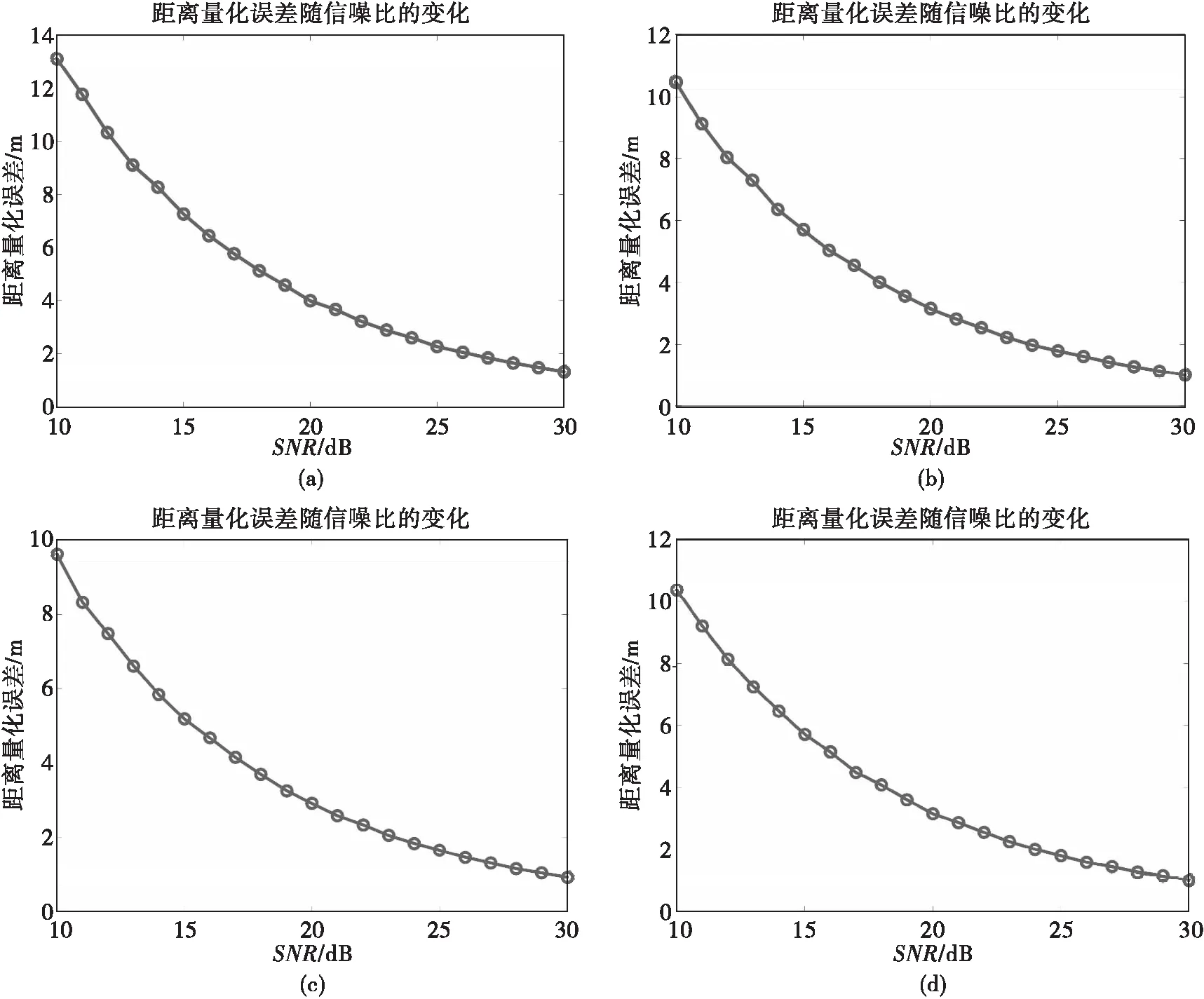
图11 不同采样位置下距离量化误差随SNR变化分析

4 结束语

本文针对雷达测距中距离量化误差的存在，结合先验信息，将回波脉压结果主瓣内采样最大值和次大值所在区间的波形近似为高斯分布函数，利用高采样率下的脉压波形仿真估计出高斯分布函数的方差，然后将实际采样率下脉压结果的最大值和次大值的位置信息和幅度信息作高斯插值处理估计出回波脉压结果的真实峰值时间，实现了减小距离量化误差的目的。

相比于抛物线插值算法[11]，高斯插值算法步骤简单，计算量小，对脉压结果中采样最大值和次大值幅度无需作归一化处理，只要将采样时间用采样率作归一化便可直接作插值运算来估计峰值时间，故误差更小。仿真结果表明，高斯插值算法可以显著地提高雷达测距精度。