同心圆排布管束圆心角对耦合振动的影响

谭 蔚 张禛庶 张天保 郭 凯

（天津大学化工学院）

管壳式换热器由于制造简单、 生产成本低，被广泛应用于石油、化工及核电等行业。 在生产过程中，换热器的安全运行非常重要，一旦发生泄漏，不仅会造成经济损失，还会污染环境［1］。 管束振动是造成管壳式换热器失效的主要原因，管束会在横向流的冲刷下产生振动，大幅振动会使管子之间发生碰撞和磨损，从而导致管束破坏。

换热器中的管子是弹性管，极易受到流动流体的影响而产生振动，而振动时又会影响其周围的流场，从而影响相邻管子的振动，因此弹性管的振动是一种耦合振动［2］。 如果将管子视为独立的个体进行研究， 则会忽略其他管子对它的影响。 管子本身的振动与响应是与其固有频率相关的。 在换热器管束流致振动设计中，附加质量系数（附加质量与被管子排开的流体质量之比［3，4］）是计算管子固有频率的基本参数。 当管束在流体中发生振动时，其固有频率会比在空气中的固有频率低。Moretti P M和Lowery R L于1976年通过激振试验，得到了不同排布方式下被刚性管包围的中心弹性管的附加质量系数与节径比之间的关系，并绘制了节径比在1.25～1.50之间的方形和三角形排布管束的附加质量系数曲线［5］。 随着计算机技术的发展，数值模拟逐渐被应用于流致振动相关问题的计算［6，7］，冯双双等基于计算流体力学理论，采用流体软件CFX及其动网格技术，给出了不同边界情况下物体的附加质量计算方法［8］。 孙雷等使用ANSYS建立了换热管的流固耦合分析模型，计算出了管束的一阶共振频率，研究了换热管的共振特性，得到了影响管子振动频率的参数［9］。 张添翼等使用ABAQUS软件建立了三维有限元分析模型，计算了快堆中间热交换器换热管束的固有频率［10］。

GB/T 151—2014中给出了4种管束排布方式的附加质量系数， 但不包含同心圆排布方式，也没有相应的设计计算方法。 为此，笔者采用数值模拟软件ANSYS CFX，通过计算同心圆排布管束在水中的固有频率，得到不同圆心角下管束发生耦合振动时的附加质量系数，为同心圆排布管束耦合振动分析提供基础参数。 在此基础上，建立了同心圆排布管束的流固耦合模型，计算分析管束在发生耦合振动时管束排布圆心角对振幅、频率等参数的影响规律，以期为同心圆排布管束的设计与工程应用提供参考。

1 管束振动频率计算

1.1 同心圆排布管束

同心圆排布管束各圈的管子数目构成等差数列，笔者研究的管阵整体结构为从内到外每一圈增加6根管子， 同心圆排布管束形式如图1所示。 由图1可知，在同心圆排布中，60°为最小重复单元，且在0～60°间排布形式关于30°线对称分布，故只需研究0～30°间不同位置处的管束振动，即可得到同心圆排布管束整体振动响应。 同心圆排布管束的排列方式会随着圆心角的变化而变化，在0°附近的管子排列方式为近似正方形排列，在30°附近的管子排列方式为近似转角三角形排列，中间部分为过渡段。 Liu L Y等通过试验和数值模拟的方法研究了同心圆排布管束圆心角0、15、30°处管束的流体弹性不稳定性，研究结果表明分布在过渡段的管子最容易发生流弹失稳现象［11］。 因此， 笔者选择的研究对象是分布在过渡段的管子。

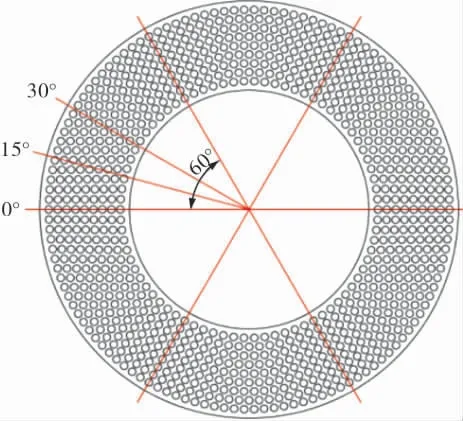
图1 同心圆排布管束形式

图2是同心圆排布管束的九管模型示意图。由图1、2可以看出， 影响同心圆排布管束管间距的参数并不是某个单一的变量，而是与管束的周向距离C、 径向距离Rd和管束所在位置的圆心角均有关。

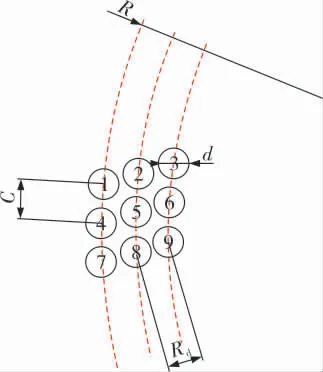
图2 同心圆排布管束的九管模型示意图

1.2 模型简化与计算设置

横向流是导致管束发生振动的主要原因，所以可将模型简化为二维模型，管子的轴向距离取1mm。 管子外径为25mm，杨志海通过建立不同尺寸的流体域边界研究了方形管束的耦合振动情况，发现当流体域边界到管束区距离大于10倍管径时，可以消除流体域边界对中心管子振动情况的影响，所以流体域直径取600mm［2］。

模拟中的分析类型为瞬态分析。 分析总时长为100s，时间步长为0.002s；将流体域的前、后表面设置为对称边界， 参考压强为一个标准大气压。 在0s时沿x方向激振中心管，计算管束在水中的固有频率时，周围的管子设置为刚性管，不会随着时间运动；计算管束耦合频率时，将周围的管子设置为弹性管， 这些管子初始为静止状态，但会受到中心管振动的影响。 数值模拟计算参数如下：

湍流模型 标准k-ε模型

壁面函数 Scalable壁面函数

收敛控制 最小系数循环1

最大系数循环20

残差 10-4

1.3 网格划分与网格无关性检验

管束的变形会改变流场的网格，所以需要采用动网格技术。 在流体域模型中心建立一个直径为100mm的圆面，将整个模型切分使管束区成为一个独立的体，对管束区使用Mesh板块中的多区域划分法（Multizone）进行划分，其他部分网格自动生成，网格划分如图3所示，在中心管处添加边界层（inflation），局部网格如图4所示。

图3 整体网格

1.4 管束的固有频率和耦合频率计算

取图1中圆心角为0～30°区间的管束作为研究对象，计算同心圆排布管束的固有频率和耦合频率。

图4 局部网格

管子在空气中的固有频率设置为19Hz。 计算管子在水中的固有频率时，将5号管（图2）设置为弹性管，其余管子设置为刚性管，激振5号管并记录其振动轨迹； 计算耦合频率时则将9根管子均设置为弹性管。

图5是单根管在水中的频谱图， 图中振幅峰值所对应的频率为管束在水中的固有频率，其值为16.48Hz。图6是考虑耦合振动的频谱图，图中出现了两个振幅峰值，对应的是管束最小耦合频率和最大耦合频率，分别为16.27Hz和17.76Hz。对比图5、6可见， 管子固有频率的大小会介于最大耦合频率和最小耦合频率之间。 当中心管周围的管子为弹性管时， 管子的频谱图中会出现多个峰值，对应多个不同的耦合频率，这个现象Chen S S等［4］曾多次提到，图6中有两个振幅峰值，这是因为部分耦合频率会叠加，计算结果中仅表现为两个。

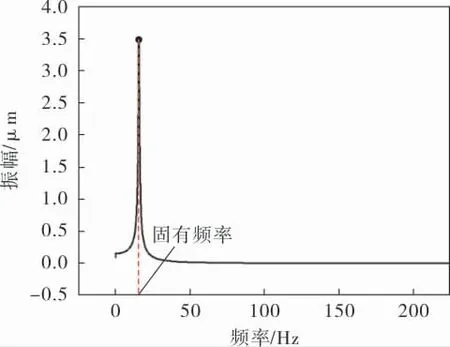
图5 单根管在水中的频谱图

图6 考虑耦合振动的频谱图

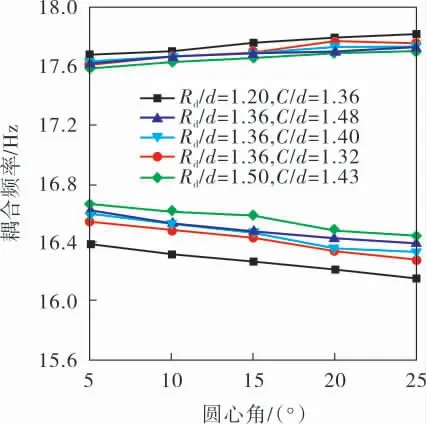
图7 中心管的耦合频率带

图7为中心管的耦合频率带，5组不同的模拟结果均显示，随着圆心角的增大，耦合频率带变宽。 以Rd/d=1.20、C/d=1.36为例，当圆心角为5°时，耦合频率带宽为1.3Hz；当圆心角为25°时，耦合频率带宽为1.6Hz，因此圆心角越大管束在振动时越容易达到耦合频率，从而产生耦合振动。 另外，当Rd/d=1.20、C/d=1.36时，耦合频率带最宽；而当Rd/d=1.50、C/d=1.43时，耦合频率带最窄，可以看出耦合频率带随着管间距的增大而变窄，所以管间距越小越容易发生耦合振动。

1.5 耦合振动时附加质量系数计算

Hassan M和Weaver D S通过悬臂梁圆柱在静水中的振动试验，推导出附加质量系数CM的计算公式如下［6］：

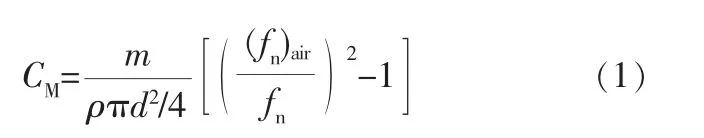
式中 fn——流体中管子的固有频率，Hz；（fn）air——空气中管子的固有频率，Hz；

m——空管质量，kg；

ρ——流体的密度，kg/m3。

采用式（1）计算同心圆排布管束发生耦合振动时的附加质量系数，绘制出了圆心角与管束附加质量系数的关系曲线 （图8）。 从图8中可以看出，同心圆排布管束在发生耦合振动时的附加质量系数不是一条曲线，而是曲线带，附加质量系数曲线带会随着圆心角的增加而变宽。

图8 圆心角与管束附加质量系数的关系曲线

2 同心圆管束耦合振动特性分析

2.1 计算设置

建立一个局部的同心圆排布管束的九管流体域模型（图9），9根管均设置为弹性管，管外的流体域介质为纯水，通过观察不同圆心角下管束耦合振动的情况，研究圆心角对管束耦合振动的影响。 耦合振动模拟时，在1号管上施加一个频率与最小耦合频率一致的正弦力， 初始方向如图9所示，使1号管在2s内的振动不会衰减，其余管子初始为静止状态。

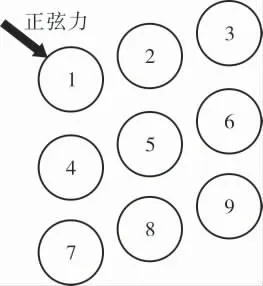
图9 九管流体域模型与正弦力方向

2.2 管束振动轨迹

图10是不同圆心角管束的振动轨迹图。 可以看出， 激振1号管时， 其他管束会产生明显的振动，管束之间存在着强烈的耦合效应，其中2、4号管振动最剧烈。

图10 不同圆心角管束振动轨迹图

对比不同圆心角的振动轨迹可知，随着圆心角的增大，管束之间的耦合效应增强。 当圆心角为25°时，管束的振幅最大，耦合振动也最为强烈，所以圆心角25°处的管子相比于5°和15°处的更容易失稳。 另外， 由于在1号管上施加了一个正弦力， 所以1号管的振动没有受到其他管子振动的影响， 第1排管子在圆心角变大的过程中主振方向基本不变； 第2排管子的主振方向随着圆心角的增大发生了改变，4、5号管在圆心角为5°时，振动轨迹近似一条斜线，当圆心角为25°时，振动轨迹变成了椭圆形，6号管的主振方向改变约为90°；第3排管子随着圆心角的增大， 主振方向有较大变化，7号管的主振方向改变约为30°，8号管的振动轨迹由圆形逐渐变为扁平的椭圆形，9号管的振动轨迹由斜线变为椭圆。 由此说明，同心圆排布管束在发生耦合振动时，圆心角的变化会对部分管子的主振方向产生影响，振动轨迹会由斜线变成椭圆，在管束发生失稳时，圆心角25°附近的管子更容易与周围多根管子发生碰撞。

2.3 管束的均方根振幅

同心圆排布管束圆心角的增大，会导致管束耦合振动振幅的增大，笔者计算了除1号管外，其余8根管子在发生耦合振动时2s内的平均振幅。通过计算发现，2、4、5号管子的平均振幅较大 （图11a）， 其余管子的平均振幅如图11b所示。 由图11a可知，管束在2s内的平均振幅会随着圆心角的增大而增大。 另外，圆心角由5°增至25°时，5号管振幅增量最小，为10.7%；2号管的振幅增量为18.9%；4号管的振幅增量为95.1%；可以看出，4号管振幅的增量远大于2、5号管， 这是因为随着圆心角的增大，同心圆排布管束沿周向间距比沿径向间距减小得更多， 因此相较于2、5号管，4号管距离被激振的1号管更近。 由图11b可知，3、6、8号管的振幅较为接近，7、9号管的振幅最小。

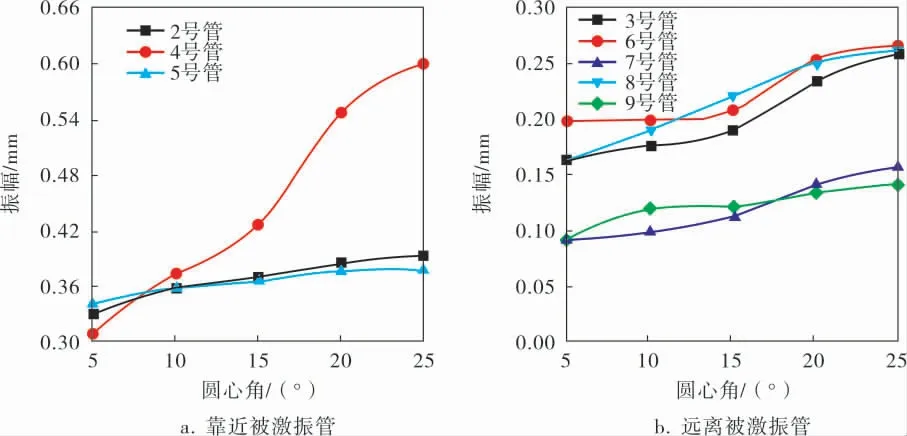
图11 不同圆心角下管子2s内的平均振幅

以上研究表明，圆心角在5～25°范围内时，随着圆心角的增大，同心圆排布管束的耦合振动增强，易发生失稳，因此在设计同心圆排布管束换热器时，圆心角为25°附近管束的管间流速应小于换热器管束的临界流速， 以保证设备的安全运行。

3 结论

3.1 在同心圆排布管束中，被弹性管包围的中心弹性管在水中被激振时，会出现不止一个耦合频率，管束固有频率的大小会介于最大耦合频率和最小耦合频率之间。 随着圆心角的增大，管束耦合频率带变宽，圆心角越大，管束越容易发生耦合振动。

3.2 得到了同心圆排布管束的附加质量系数计算图，为工程设计提供了基本参数。 研究表明，在同心圆排布管束中，随着圆心角的增大，被弹性管包围的中心弹性管的附加质量系数曲线带会变宽。

3.3 在同心圆排布管束间发生耦合振动时，随着圆心角的增大，同心圆排布管束的耦合振动会增强。 在本文研究的条件下，管束的最大振幅增量会达到95.1%，最小振幅增量约为10.7%，圆心角越大越容易发生失稳。 因此，在设计同心圆排布管束热交换器时，建议重点关注圆心角为25°附近管束的振动响应，在实际运行中，管间流速应小于临界流速，以保证设备的安全运行。