基于滑模观测器的煤矿带式输送机用永磁同步电动机控制系统研究

晋城煤炭规划设计院 山西晋城 048000

在 煤矿运输系统中带式输送机是重要设备之一。近年来，国外单机带式输送机运距已超过 30 km，已在澳大利亚矿山投入使用；在德国煤矿使用的大型带式输送机，其输送量己达 37 500 t/h，运行速度达 7.4 m/s。目前国产带式输送机的理论研究越来越受到重视，在大运量输送机控制技术和远程控制领域取得了长足的进步，逐渐淘汰了传统的驱动方式。随着永磁同步电动机 (Permanent Magnetic Synchronons Motor，PMSM) 及其控制系统的发展，煤矿带式输送机的驱动方式也更加智能，设计一种高效、智能的带式输送机控制系统，对建设现代化、智能化矿井具有十分重要的意义。

笔者设计了一种以滑模观测器 (Sliding Mode Observer，SMO) 算法为基础的 PMSM 驱动的带式输送机控制系统，通过分析 PMSM 两相静止坐标系下的数学模型，提出了基于锁相环转子位置估计的SMO 算法，进而搭建了基于 SMO 算法的 PMSM 无位置传感器控制系统仿真模型，并通过仿真结果分析验证了该控制系统的有效性和合理性。

1 带式输送机驱动系统分析

1.1 异步电动机驱动系统

传统的带式输送机驱动系统主要由异步电动机、减速器和联轴器组成，如图 1 所示。异步电动机驱动系统具有便于操作、启动转矩小及控制系统简单等优点；其缺点是启动电流较大、控制精度差、传动效率低、能耗高，联轴器和减速器故障率高，后期维护费用较高。

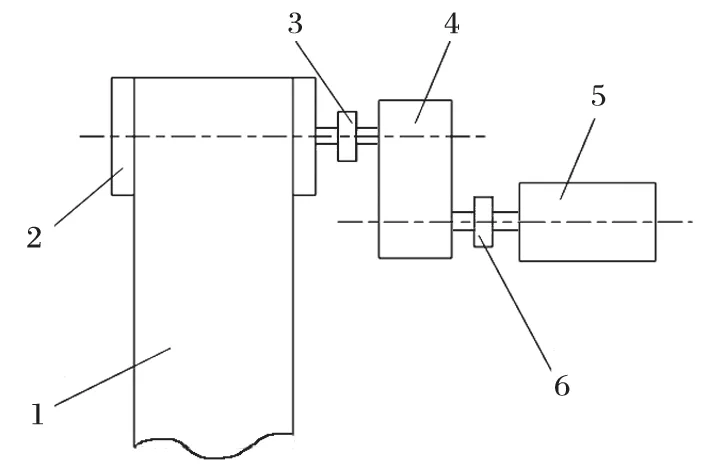
图1 异步电动机驱动示意Fig.1 Sketch of asynchronous motor drive

1.2 PMSM 驱动系统

新型的带式输送机驱动系统主要由 PMSM 和变频器组成，如图 2 所示。与异步电动机驱动系统相比，PMSM 驱动系统传动效率高，能耗较低，节约电能；电动机启动转矩大，具有较强的过载性能和软启动性能；系统结构简单、便于维护；变频调速性能高，多电动机驱动时功率平衡性好[1]。因此，选用由PMSM 和变频器组成的新型带式输送机驱动系统具有十分明显的优势。

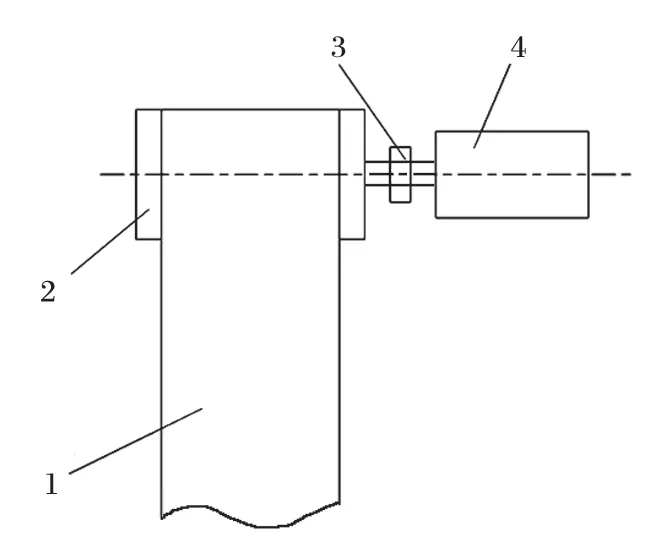
图2 PMSM 驱动示意Fig.2 Sketch of PMSM drive

2 带式输送机控制系统数学模型

2.1 PMSM 数学模型

在 PMSM 的控制方式中，滑模控制是一种特殊的变结构控制，它将电动机作为一种离散型的系统进行控制，表现为控制的不连续性和非线性。该控制系统的转速响应在相平面里跟踪转速的估计值，具有较强的鲁棒性，不受 PMSM 参数和负载变化的影响。SMO 控制结构简单，将控制系统的状态变量控制在滑模面上进行高频率、小幅度的滑模运动[2]。笔者设计的 SMO 算法是基于静止坐标系α-β下的数学模型，PMSM 电压方程为[3]

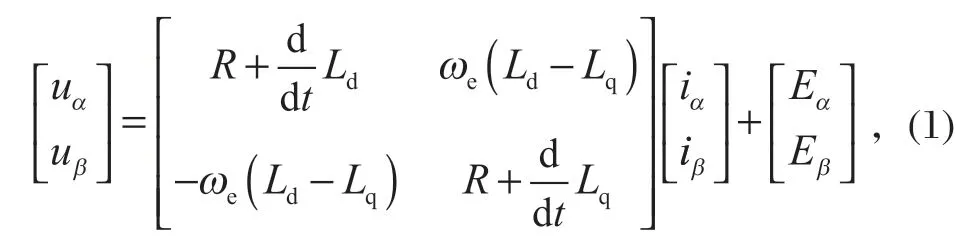
式中：[uαuβ]T为定子电压；R为定子电阻；Ld、Lq为定子电感；ωe为电角速度；[iαiβ]T为定子电流；[EαEβ]T为扩展反电动势[4]，且满足

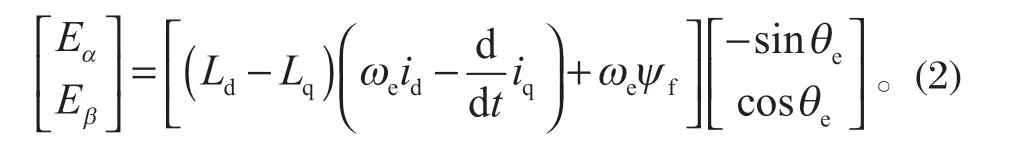
式中：ψf为永磁体磁链；θe为转子位置角。

由式 (2) 可知，PMSM 的扩展反电动势包含电动机转子位置和转速的全部参数，只有准确获取扩展反电动势，才可以计算出电动机的转速和转子位置信息。为便于用 SMO 来观测扩展反电动势，将式 (1) 改写为电流状态方程，

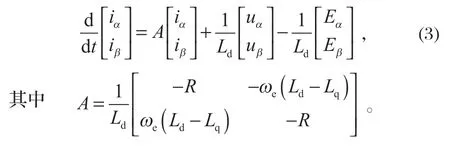
2.2 SMO 数学模型

2.2.1 SMO 的设计

定子电流观测值方程为

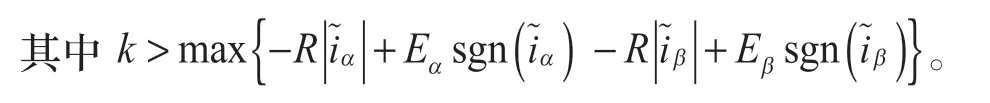
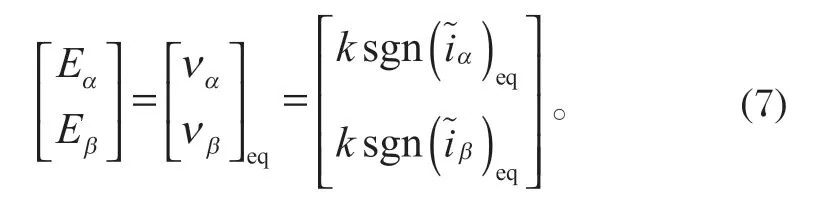
2.2.2 基于锁相环的转子位置估计

根据式 (2)，SMO 算法需要进行反电动势信号的提取，而传统 SMO 的 PMSM 无位置传感器控制系统采用的是低通滤波器。低通滤波器会造成转子位置估算的相位延时，使控制系统产生较大的抖振，转子位置的估计值存在一定的高频波动[5]。采用基于锁相环的转子位置估计算法能够有效减小系统抖振和相位延时。因此，笔者采用锁相环系统估算转子位置信息，其原理框图如图 3 所示[6]。

图3 锁相环原理框图Fig.3 Principle block diagram of phase locked loop (PLL)

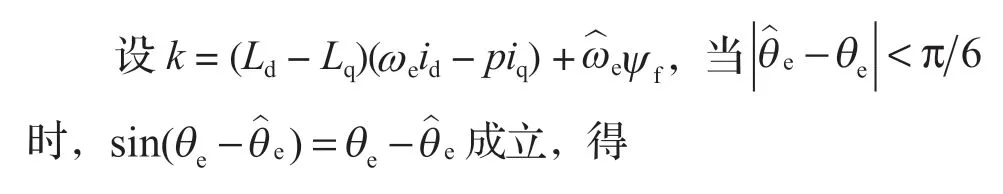
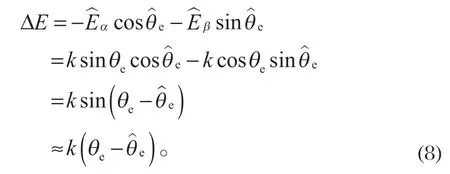
由式 (8) 可知，锁相环原理可以等效为图 4 的框图。

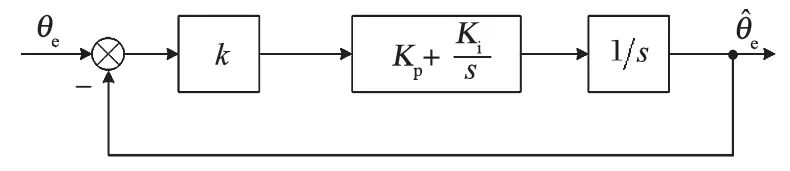
图4 锁相环等效框图Fig.4 Equivalent block diagram of PLL

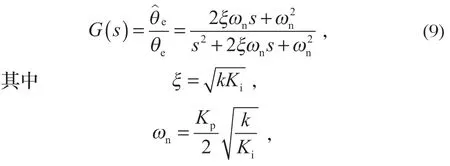
式中：ξ为 PI 调节系数；ωn为电动机转速变化值。

2.3 基于 SMO 的 PMSM 无位置传感器控制原理

基于 SMO 的 PMSM 无位置传感器控制方法，采用id=0 的控制策略，在传统的矢量控制原理的基础上，增加无位置传感器的控制策略。其中转速给定值和转子位置值均使用 SMO 算法计算出的估计值，从而避免了机械传感器的使用[7]。基于 SMO 的 PMSM无位置传感器控制原理框图如图 5 所示。

3 基于 SMO 的 PMSM 控制系统仿真建模

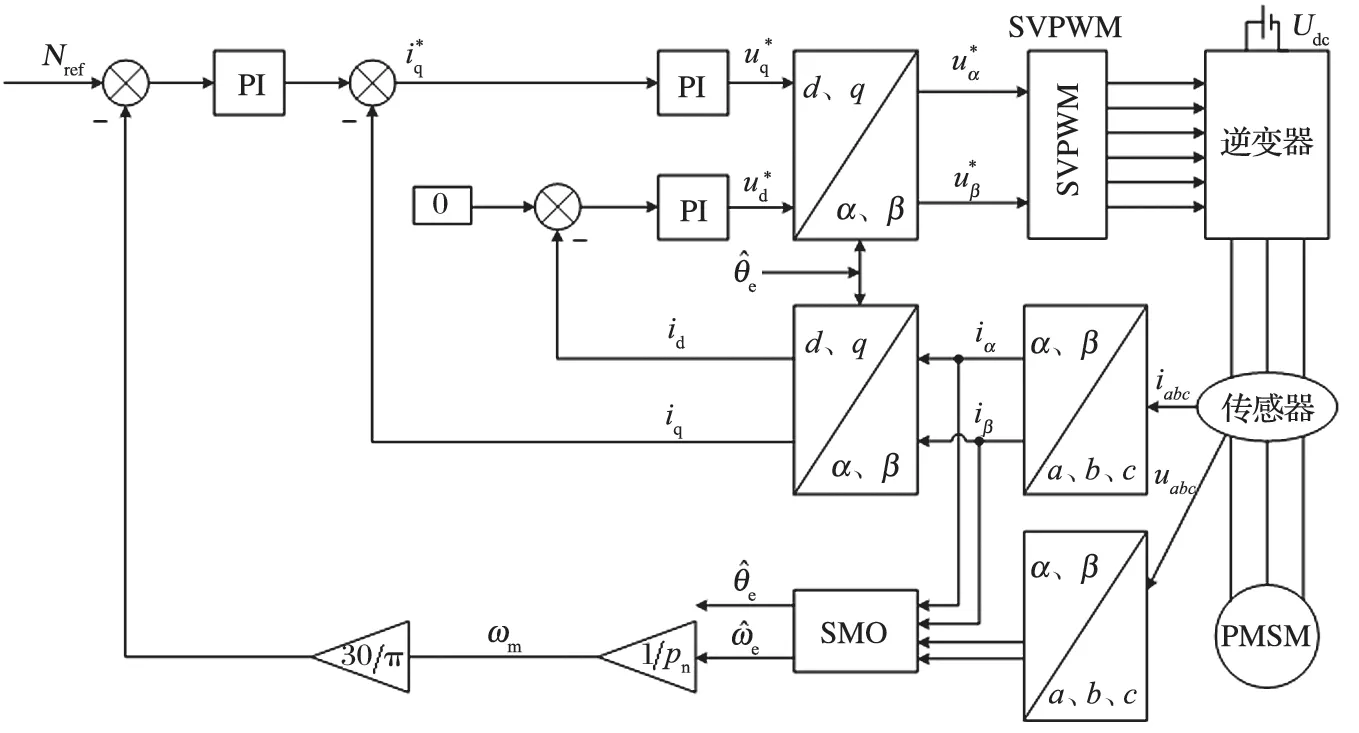
图5 基于 SMO 的 PMSM 无位置传感器控制原理框图Fig.5 Block diagram of PMSM non-position sensor control based on SMO

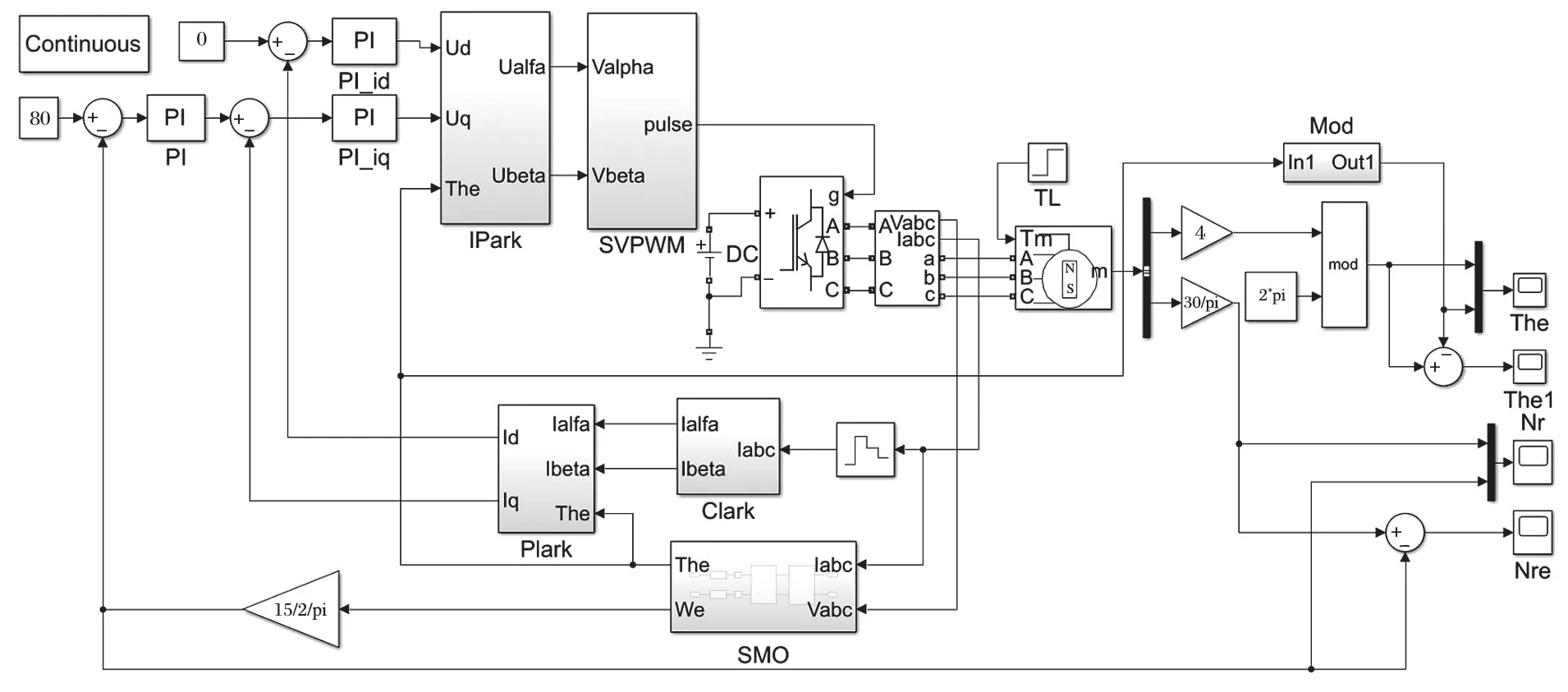
图6 基于 SMO 的 PMSM 无位置传感器控制系统仿真模型Fig.6 Simulation mode of PMSM non-position sensor control system based on SMO

根据图 5 搭建了控制系统的仿真模型，如图 6所示。仿真模型由 PMSM 模块、SMO 仿真模型、SVPWM 控制模块、Plark 变换模块和 Clark 变换模块组成[8]。仿真模型中 PMSM 仿真参数设置如表 1 所列。

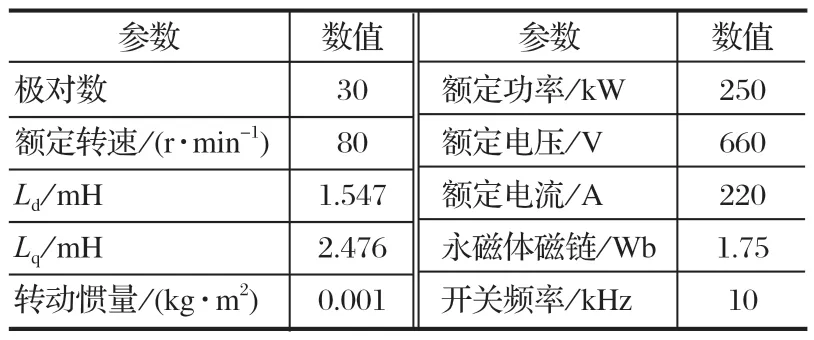
表1 PMSM 仿真参数Tab.1 Simulation parameters of PMSM

SVPWM 控制模块仿真模型如图 7 所示，基于锁相环算法的 SMO 仿真模型如图 8 所示，锁相环算法的仿真模型如图 9 所示，滑模观测器的仿真模型如图10 所示。

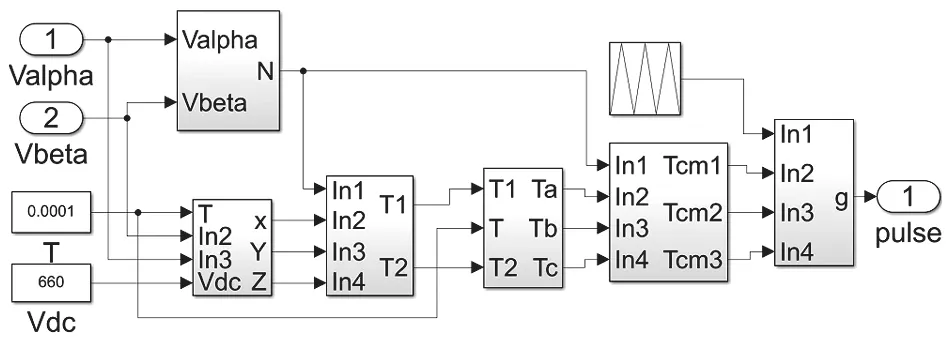
图7 SVPWM 控制模块仿真模型Fig.7 Simulation model of SVPWM control module

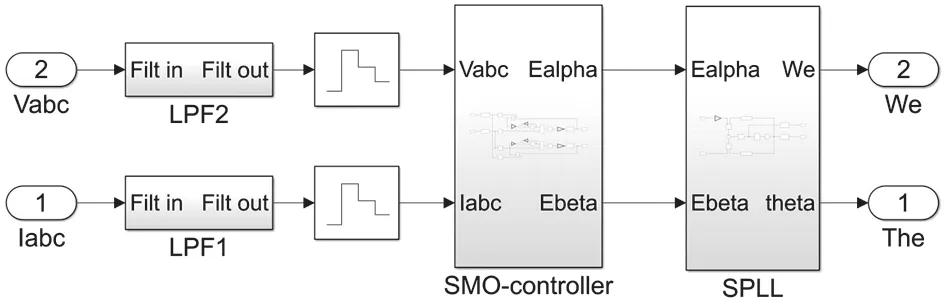
图8 基于锁相环算法的 SMO 仿真模型Fig.8 SMO simulation model based on PLL algorithm

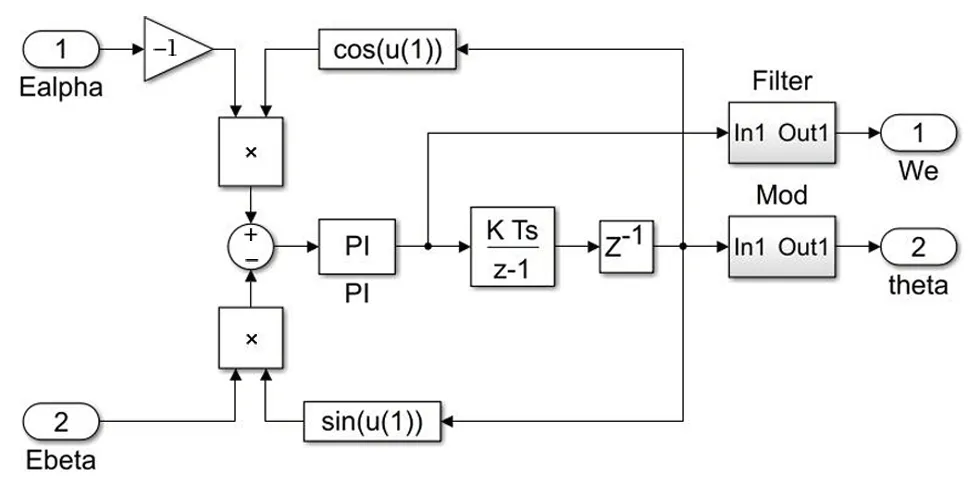
图9 锁相环算法的仿真模型Fig.9 Simulation model of PLL algorithm

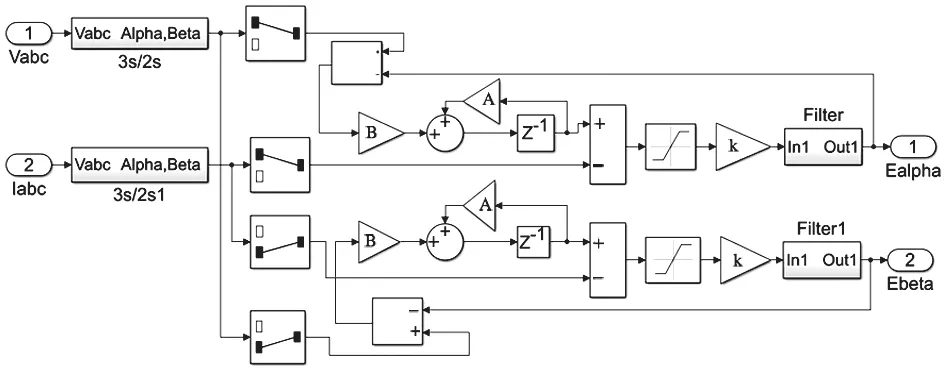
图10 滑模观测器的仿真模型Fig.10 Simulation model of SMO

4 仿真结果及分析

PMSM 给定转速设定为 80 r/min，仿真时间设定为 0.5 s。PMSM 在 0.5 s 内的转速估计值和实际值波形对比如图 11 所示。由图 11 可以看出，PMSM 的实际转速很快能达到给定值，转速估计值和实际值波形基本重合，电动机在达到稳定转速后有 3 r/min 的波动，偏差小于 4%。

PMSM 转子位置估计值和实际值的波形对比如图 12 所示，电动机转子位置估计的电角度和实际的电角度波形基本重合，转子位置估计值误差较小。PMSM 转子位置估计误差变化波形如图 13 所示。在电动机启动时转子位置估计误差较大，最大为 0.43 rad；在 0.25 s 附近时转速趋于稳定，能够十分精确地跟踪转子位置。

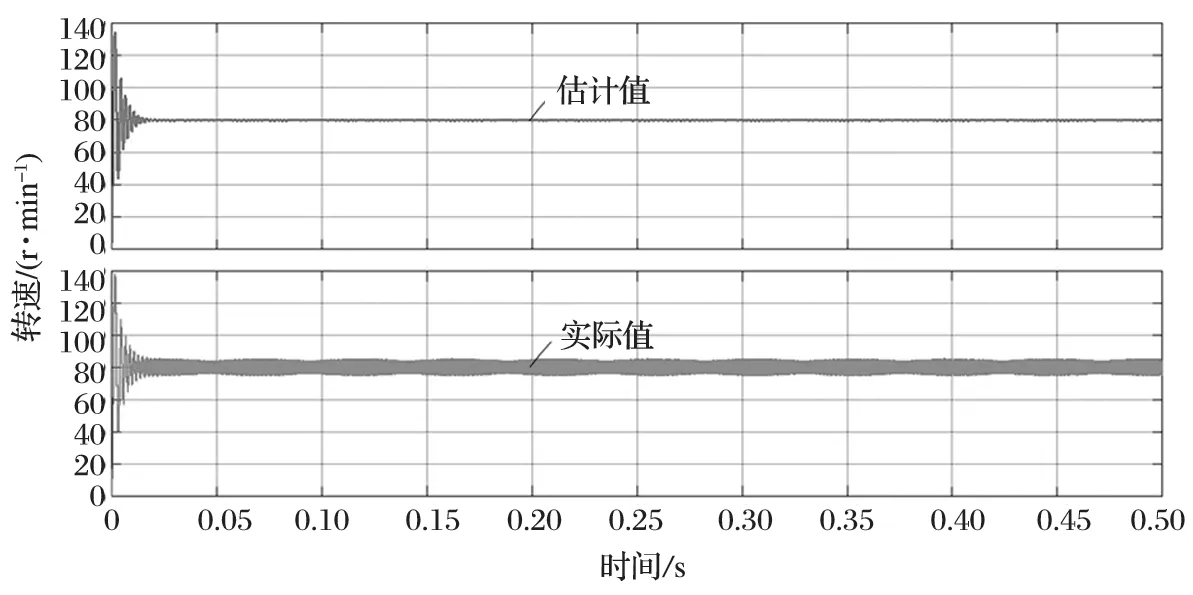
图11 转速估计值和实际值波形对比Fig.11 Comparison between waveform of estimated speed value and actual one

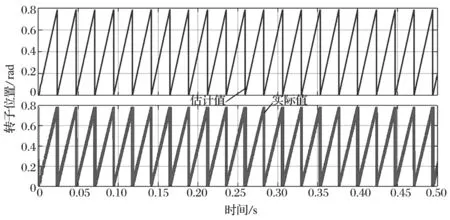
图12 转子位置估计值和实际值波形对比Fig.12 Comparison between waveform of estimated rotor position value and actual one

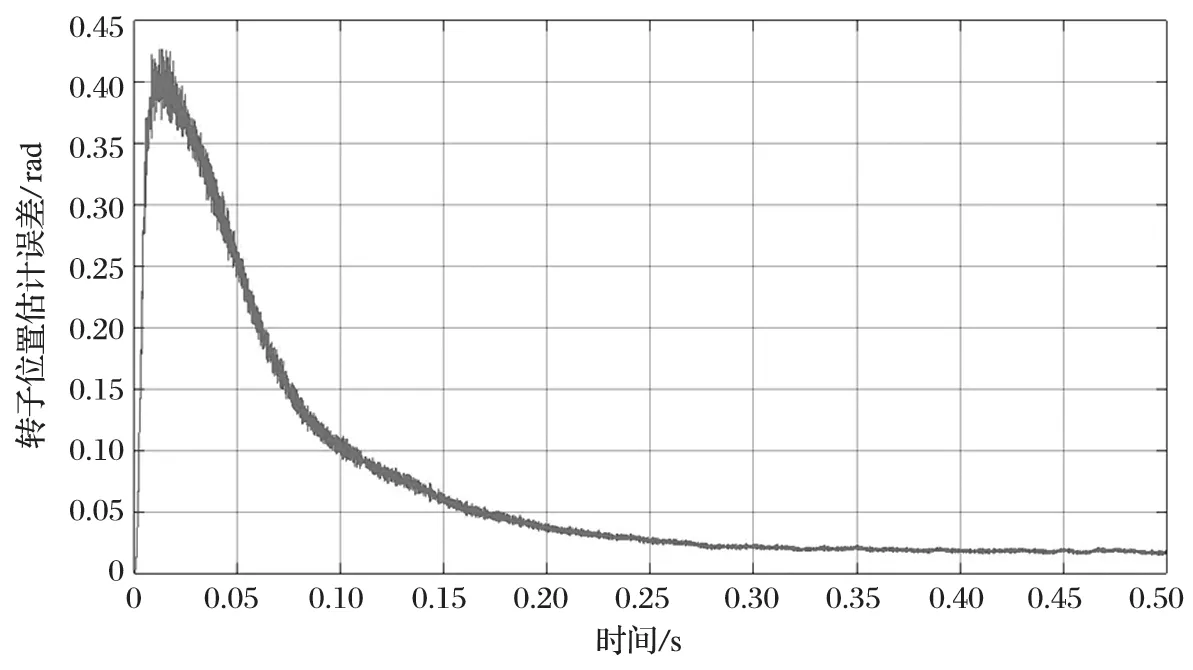
图13 转子位置估计误差波形Fig.13 Waveform of estimation error of rotor position

5 结论

在分析了由 PMSM 和变频器组成的新型带式输送机驱动系统的基础上，建立了α-β坐标系下的PMSM 的数学模型和 SMO 的数学模型，在 MATLAB/Simulink 仿真软件中搭建了基于 SMO 算法的 PMSM无位置传感器控制系统仿真模型，并对仿真结果进行了分析，为新型带式输送机驱动控制系统的设计提供了依据。仿真结果证明了基于 SMO 的带式输送机用 PMSM 控制系统具有调速性能好、转速波动小等优点，能够准确跟踪转子位置，转速估计值精度高，控制系统设计合理，在煤矿带式输送机中具有广阔的应用前景。