高精度地下铰接式车辆全液压转向动力学建模
2021-04-19邱林宾
邱林宾,曹 鑫,金 纯
1北京科技大学 北京 100083
2山东黄金集团烟台设计研究工程有限公司 山东烟台 264006
铰 接式无轨车辆具有高效、高机动等特点,广泛应用于地下矿山的凿岩、支护、铲装、装药和运输作业。随着地下矿山开采深度的增加,高温、高应力、高渗透压力以及开采扰动问题日益突出,使得开采难度增大,严重威胁地下采矿人员的安全与健康。因此,地下铰接式无轨车辆的智能化和无人化具有重要的意义[1-2]。
路径跟踪控制是无人驾驶车辆的关键技术,其目的是使车辆的航向偏角和横向误差趋近于零。目前的路径跟踪技术通常采用比例-积分-微分、纯跟踪控制、前馈-反馈控制、线性二次型调节跟踪控制器和模型预测等方法来控制车辆动力学模型,通过向模型提供实时的质心侧偏角或横摆角速度等数据来实现闭环控制[3]。这些控制算法均以被控车辆的模型为基础,通过不同的算法和理论实现精准控制;因此,被控模型的精度以及反馈数据的可靠性与稳定性,对消除误差、提高路径跟踪精度非常重要。
车辆的转向动力学模型是目前研究操控稳定性、路径跟踪的主要手段。基于研究铰接式车辆的速度和质心与操控稳定性之间的关系,Horton 等人[4]建立了铰接式车辆转向模型,分析了模型转向特性的仿真结果,认为速度和质心是导致铰接式车辆振荡和指数不稳定的关键参数。针对铰接式车辆的蛇行问题,He等人[5]建立了 3 自由度模型,分析了转向特性对车辆侧向稳定性的影响;Azad 等人[6-7]通过对铰接式车辆转向特性分析,研究了车辆结构参数和临界速度与蛇形运动之间的关系;Pazooki 等人[8]在动力学模型的基础上进一步加入了铰接车体的运动学模型,研究了转向系统的转向响应与横摆稳定性之间的关系,认为转向速率增加会导致车体横摆振动加剧。
上述研究通过建立铰接式车辆转向系统动力学模型,基于非线性动力学和稳定性分析理论研究了车辆速度和结构参数与操控稳定性之间的关系,为铰接式车辆的控制提供了重要依据;但是在建模中将油液体积弹性模量视为常量,未考虑油液的可压缩性,使得铰接式车辆的模型精确性不足,转向特性不清晰,控制误差大,系统需反复调节,导致铰接式车辆蛇行前进。
针对铰接式车辆的结构特点及转向运动学关系,分别建立了铰接式车辆动力学模型及转向液压模型,并考虑传动液体的可压缩性,建立气液两相有效体积弹性模量模型。采用实车试验获得的车辆和转向系统状态参数,分别在时域和频域上对所建立的模型进行验证,期望能够获得反映实际转向特性的地下铰接式车辆的转向模型。
1 铰接式车辆动力学模型
铰接式车辆分为前后 2 个车体,以铰接方式联接。铰点两侧安装有左右对称的转向液压缸。转向时,通过控制转向液压缸的伸缩,改变前后车体之间的相对角度,实现整车的转向。铰接式车辆动力学模型可分为轮胎动力学模型和液压转向模型 2 个部分。
1.1 轮胎动力学模型
在铰接式车辆行驶过程中,绕垂直轴的横摆力矩是导致蛇行运动的主要因素,因此,在建模过程中忽略沿车辆行驶方向和侧向的倾斜和俯仰运动。简化后的铰接式车辆受力简图如图 1 所示,铰接点处的受力分析如图 2 所示。模型包含了车轮运动在内的 12 个自由度。
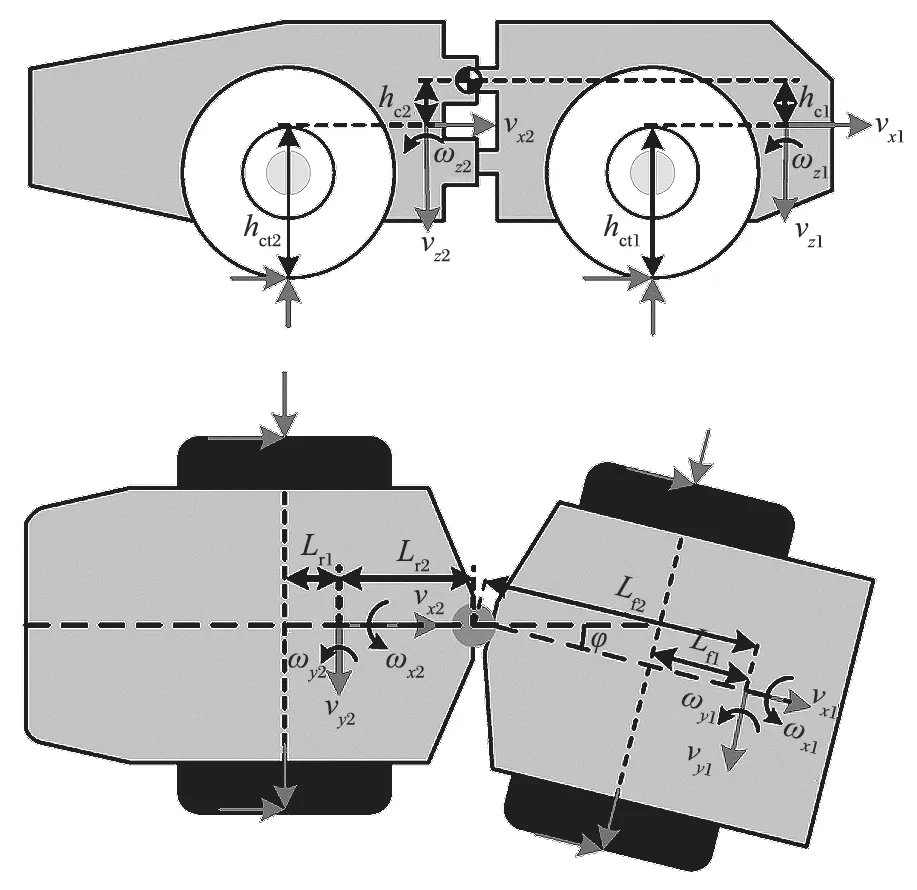
图1 铰接式车辆受力简图Fig.1 Force sketch of articulated vehicle
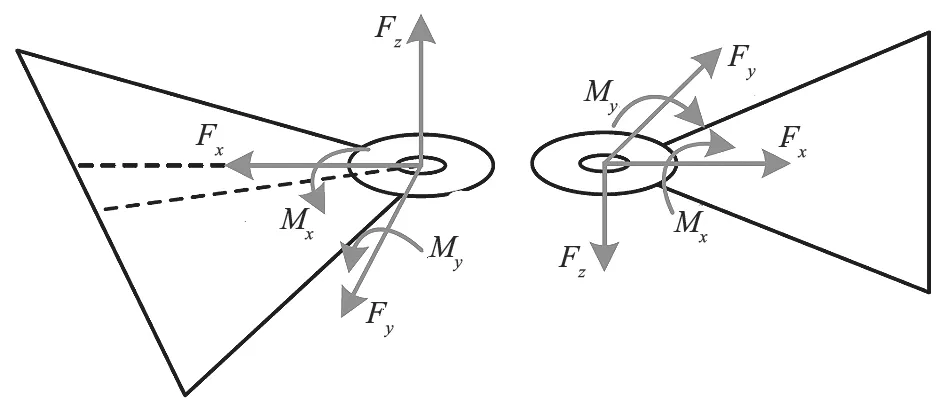
图2 铰接点处受力分析Fig.2 Force analysis at articulated joint
根据牛顿第二定律,前后车体在不同方向的动力学模型为
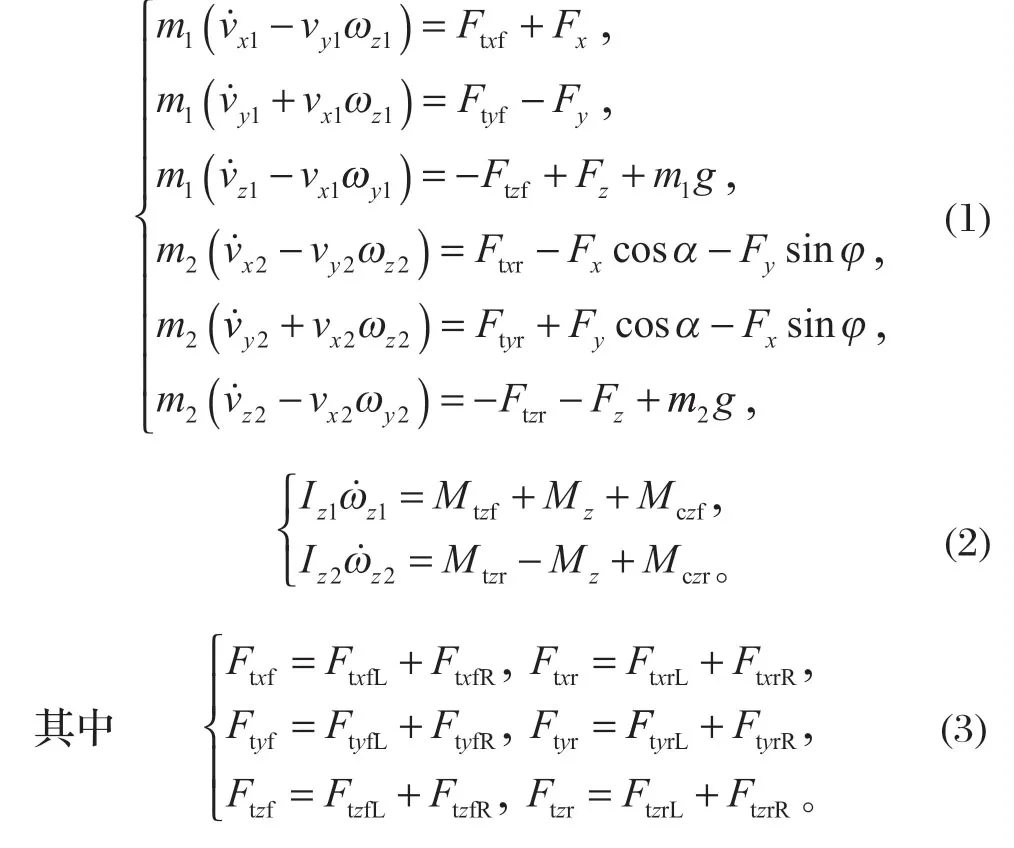
式中:1、2 分别表示前、后车体;ϕ为铰接角;m1、m2分别为前、后车体质量;Iz1、Iz2分别为前、后车体在z轴的转动惯量;Fx、Fy和Mz分别为铰接点的力和力矩;Ftxf、Ftyf、Ftxr、Ftyr和Mzf、Mzr分别为由转向液压缸引起的力和力矩;Ftxf、Ftxr、Ftyf、Ftyr、Ftzf和Ftzr分别为x、y、z方向的轮胎力。
轮胎纵向力和侧向力模型表示为
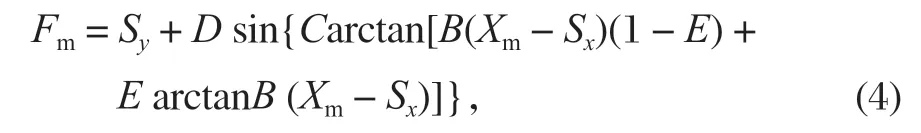
式中:Xm为滑移率。滑移率模型为
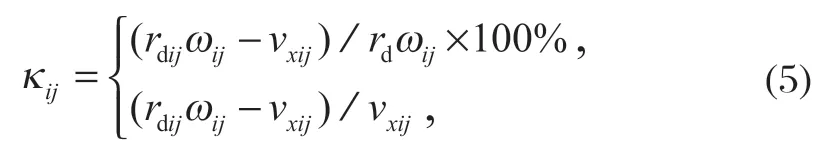
式中:vxij为各轮在中心处沿x方向的速度,i=L、R,j=f、r。
其中各轮的纵向速度可表示为
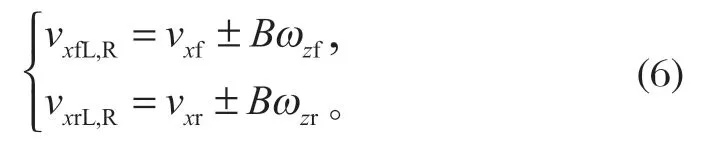
轮胎侧偏角可表示为
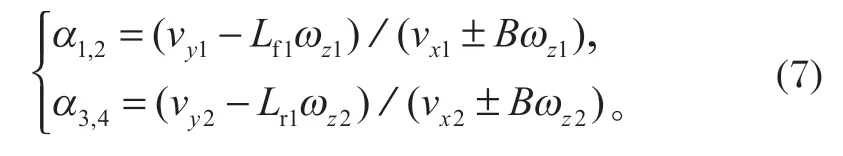
前后车体的运动学约束可表示为
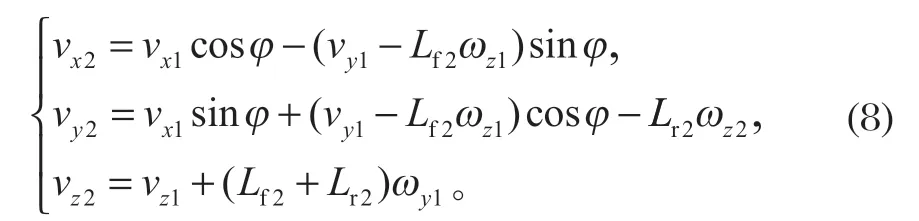
式中:Lf1为前车体质心到前车轴的纵向距离;Lr1为后车体质心到后车轴的纵向距离;Lf2为前车体质心到铰接点的纵向距离;Lr2为后车体质心到铰接点的纵向距离;B为轮距的一半。
1.2 液压转向模型
铰接式车辆通过液压油传递转向动力,其转向液压系统如图 3 所示。通过换向阀控制液压油的流向,从而控制左右转向液压缸的伸缩,实现车体的转向。
铰接式车辆的转向主阀具有阀前压力补偿功能,可以调节入口压力和负载压差保持不变,因此流入系统的流量只与阀芯开口大小有关;而出口处流量由阀芯开口和压差决定。铰接式车辆转向液压系统流入流出系统的流量可表示为
式中:Iin为转向输入电流,与qin的特性关系如图 4所示。
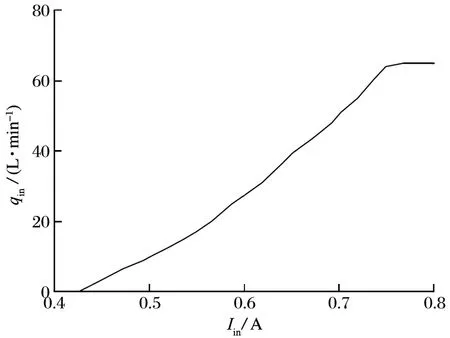
图4 转向控制阀流量特性Fig.4 Flow characteristics of steering control valve
由图 4 可以看出,转向系统的入口和出口流量均包含两部分,且满足关系:

式中:qL1、qL2分别为左转向液压缸的有杆腔和无杆腔流量;qR1、qR2分别为右转向液压缸的有杆腔和无杆腔流量;A1、A2分别为转向液压缸的有杆腔和无杆腔面积;XL、XR分别为左、右转向液压缸的伸缩量;k为油液弹性模量;Cip为转向液压缸内泄系数;Vij(i=L、R,j=1、2) 分别为左、右转向液压缸有杆腔和无杆腔内油液体积;pij(i=L、R,j=1、2) 分别为左、右转向液压缸有杆腔和无杆腔内油液压力。
由转向液压缸液压系统特性和主阀的方向特性可知,
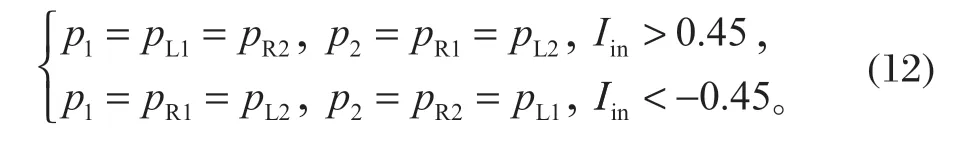
其中油液体积变化考虑管路中的油液体积,

式中:VP为转向液压缸管路中的油液体积。
转向液压缸的力平衡方程为
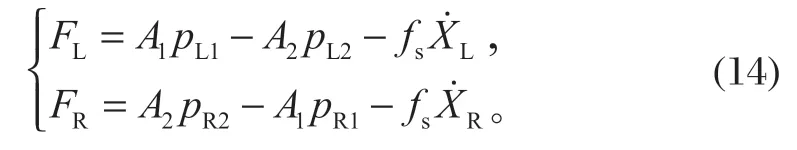
式中:fs为动摩擦因数。
铰接转向的前后车体与中间铰点之间的运动学关系如 5 所示。
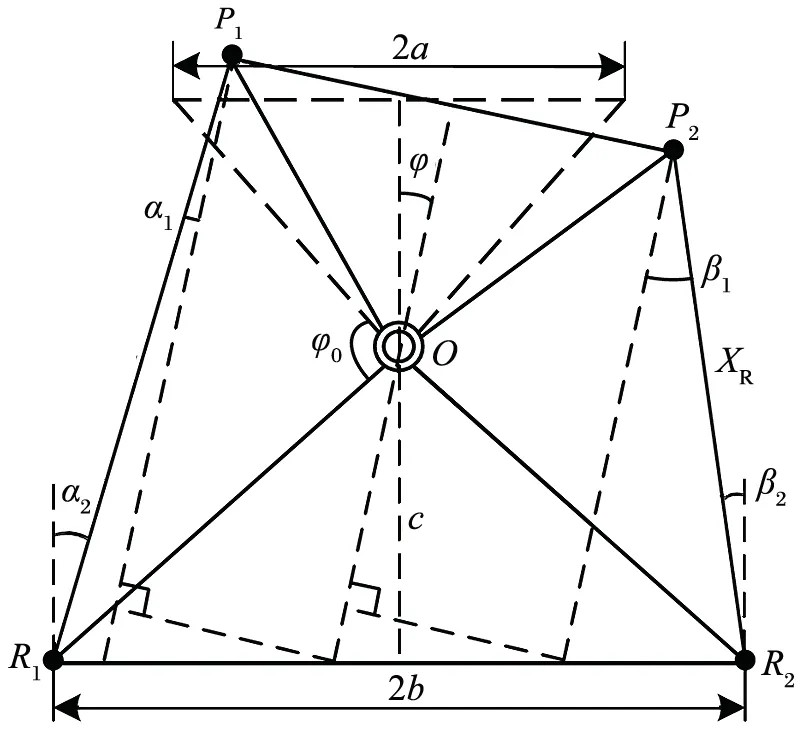
图5 铰接转向运动学关系图Fig.5 Kinematics diagram of articulated steering
由转向系统的运动学关系可得左右转向液压缸位移表达式为
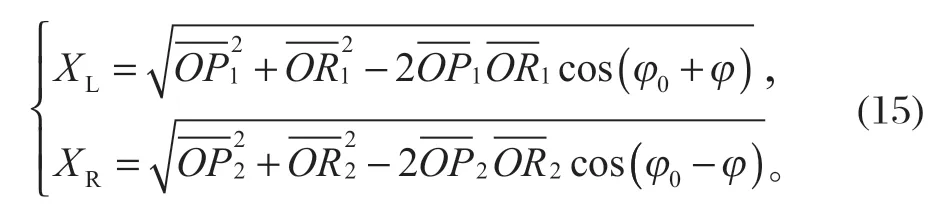
左、右转向液压缸与前、后车架之间夹角的关系可表示为

式中:r1、r2分别为左转向液压缸与前、后车架之间的夹角;b1、b2分别为右转向液压缸与前、后车架之间的夹角。
其中转向液压缸与前车架之间夹角可根据正弦定理表示为
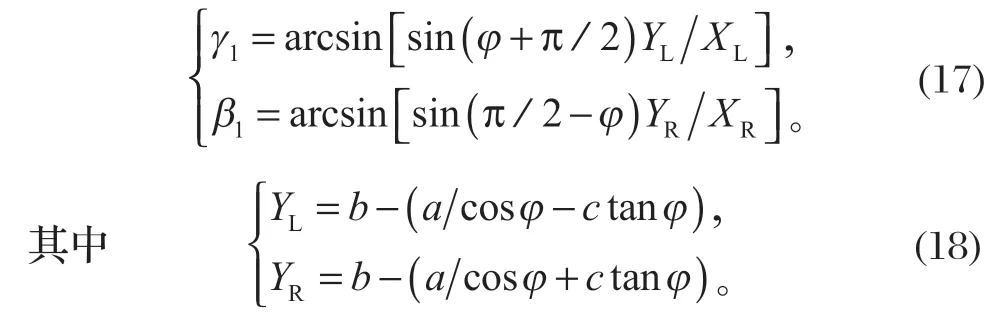
式中:YL、YR分别为左、右转向液压缸与后车架铰点之间的距离;a、b、c均为转向结构参数。
根据图 5 中运动学关系,并结合式 (14)~ (18),可得铰接转向系统对前后车体的力和力矩表达式为
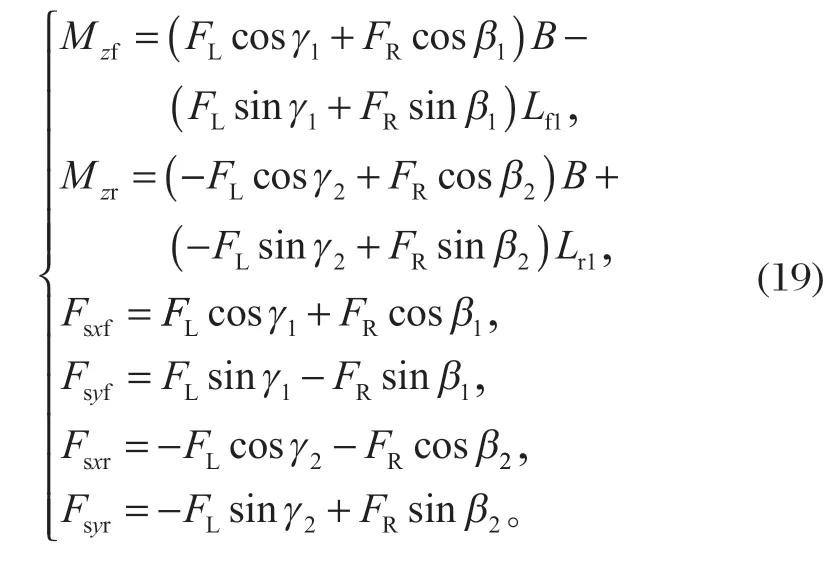
上述铰接车辆转向系统模型中,系统输入为控制电流,系统输出为施加于铰接车体的力。其中铰接转向系统与铰接式车辆整车关系如图 6 所示。
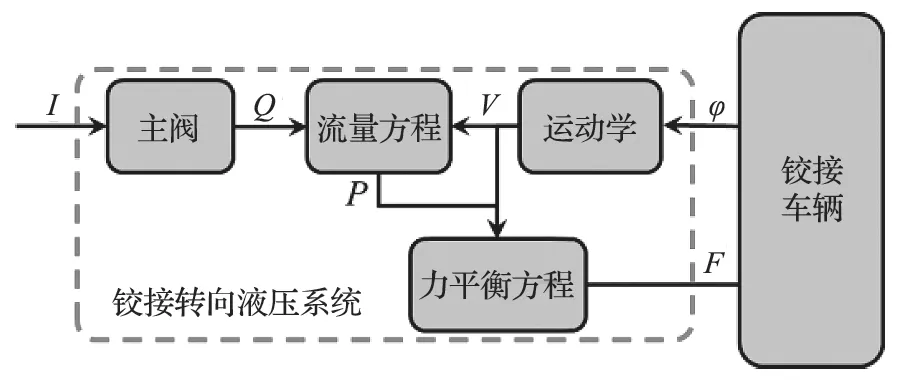
图6 铰接转向液压系统与整车关系Fig.6 Relationship between articulated steering hydraulic system and vehicle
体积弹性模量是油液的固有属性,可以表征传动过程中的压缩特性,对传动的准确性有很大的影响。静态分析时,通常认为油液的体积弹性模量是不变的常量,但在液压系统压力变化大的动态工况时,需要引入有效体积弹性模量来表征油液在实际工况中的压缩特性。笔者采用 Nykanen 模型作为油液有效体积弹性模量E的模型。
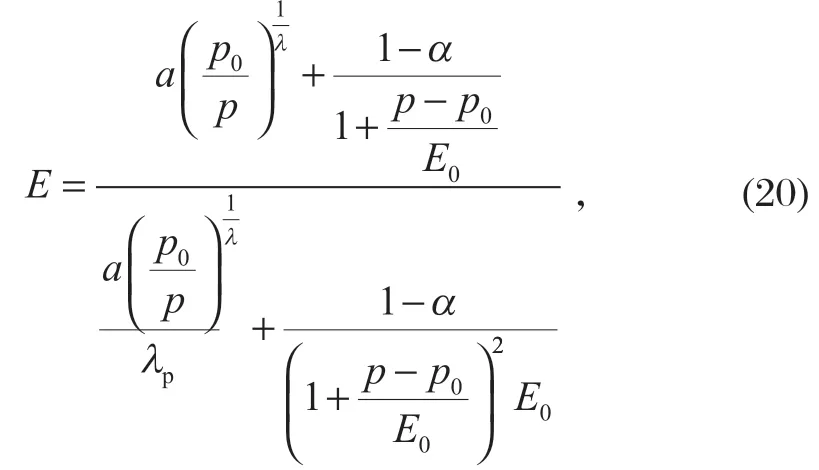
式中:p0为一个标准大气压;p为当前大气压;λ为空气的热容比;α为油液的空气含量;E0为大气压力下纯液压油液的体积模量;λp为当前大气压下的热容比。
2 模型试验验证
2.1 地下铰接式车辆现场试验
以 3 m3遥控地下铲运机为试验对象,搭建车身状态和转向系统测试系统,如图 7 所示。通过 RS232串口连接遥控模块,借助串口通信软件记录遥控器的输入信号;利用 32 通道 LMS-SCADAS 数据采集系统采集并记录试验过程中的各传感器数据。在前后车体安装陀螺仪,测量车辆行驶过程中的航向角和角速度,在中间铰接处安装角度传感器测量铰接角,在变速箱输出轴处安装编码器获取车速。在左右转向液压缸的无杆腔附近安装压力传感器,测量铲运机转向行驶过程中的转向压力;在左右转向液压缸的缸筒和缸杆之间安装位移传感器,测量液压缸长度变化量。

图7 地下铲运机现场试验系统Fig.7 Field test system for underground LHD
为了更加真实地模拟地下巷道内铲运机的工作过程,设置行驶路线为地下铲运机在巷道内铲运矿石的一个典型循环工况,如图 8 所示。其中L1为 60 m,L2为 18 m。
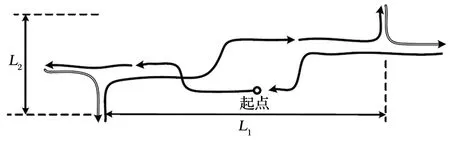
图8 现场试验行驶路线Fig.8 Driving path in field test
2.2 动力学模型时域验证
将采集到的车速和转向输入信号作为仿真模型的输入,得到仿真数据。在相同的输入下,仿真油液体积弹性模量为常值与稳态模型下铰接角的响应,并与试验结果进行对比,结果如图 9 所示。由图 9 可以看出:不同的体积弹性模量下,铰接角的仿真数据与试验数据在趋势上基本一致,但仿真数据与试验数据之间误差较大;而采用稳态模型时,仿真数据与试验数据误差较小,更接近实际转向响应。因此在铰接式车辆转向系统建模时,应考虑油液的可压缩性,且油液的体积弹性模量应视为稳态模型。
转向液压缸位移的仿真与试验结果对比如图 10所示。由图 10 可以看出,在大幅度和小幅度转向过程中,仿真中的转向液压缸位移变化趋势与试验数据吻合,位移最大差值仅为 0.012 m。

图9 不同弹性模量转向特性Fig.9 Steering characteristics at various elastic moduli

图10 转向液压缸位移仿真与试验结果对比Fig.10 Comparison between simulation results and test ones of steering cylinder displacement
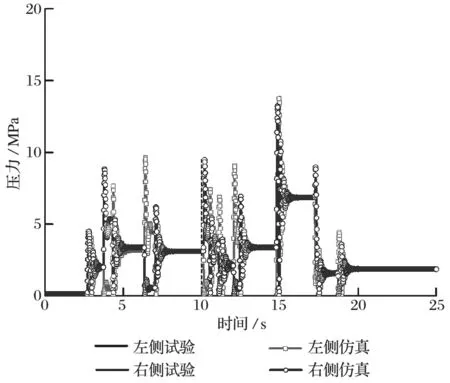
图11 转向液压缸压力仿真与试验结果对比Fig.11 Comparison between simulation results and test ones of steering cylinder pressure
转向液压缸压力仿真与试验结果对比如图 11 所示。由图 11 可以看出:在转向过程中,仿真数据与试验数据在趋势和具体数值上都一致;而在转向结束后,试验数据表现出压力反复波动,且衰减不明显,仿真数据也同样出现波动,但衰减较快,且衰减后的仿真与试验数据一致。在试验过程中发现,转向结束后前后车体出现明显摆动。
2.3 动力学模型频域验证
考虑在实车试验转向过程中,时间较短,并且信号不是连续平稳,因此采用短时傅里叶变换。在进行短时傅里叶变换时,考虑到信号波动的频率较低,并且信号中存在常值分量,采用 BEADS 算法去除信号中的常值分量,再对仿真与试验所得的后车体横摆角速度和左侧转向液压缸压力数据进行短时傅里叶变换,结果如图 12、13 所示,由图 12 可知,在每次转向动作结束后,频谱中出现 3.9 Hz 的主频,此为压力和角速度波动的频率值,仿真数据与试验数据的峰值频率出现位置相同,均为 3.9 Hz。由此可知,仿真模型转向结束后的振动频率与实车试验数据一致。

图12 后车体横摆角速度铰接角试验与仿真短时傅里叶变换对比Fig.12 Comparison between short-time Fourier transform of test and simulation data of yaw rate of rear frame
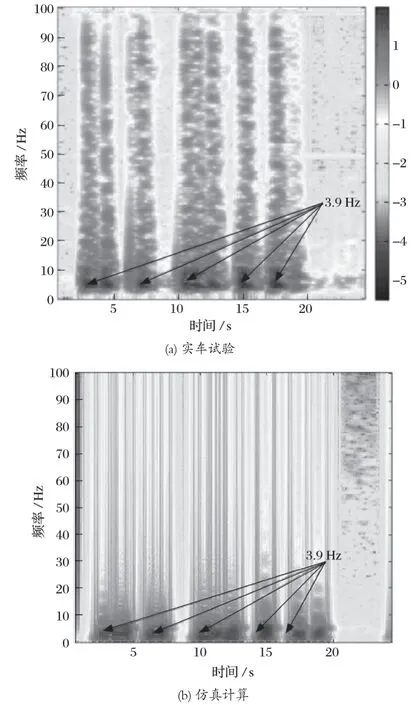
图13 左侧转向液压缸压力试验与仿真数据短时傅里叶变换对比Fig.13 Comparison between short-time Fourier transform of test and simulation data of left steering cylinder pressure
3 结论
(1) 液压油液体积弹性模量设置为常值时,模型中转向铰接角的响应与实际响应之间误差较大,而液压油液体积弹性模量采用稳态模型时,铰接角的仿真数据更接近实际转向响应。因此,在铰接式车辆转向系统建模时,应考虑油液的可压缩性,且油液体积弹性模量应采用稳态模型。
(2) 所建立的铰接式车辆全液压转向模型能够较为精确地反映铰接式车辆的转向特性,对研究该类型车辆无人驾驶的操控稳定性控制及路径跟踪控制具有一定的参考价值。
