低年段教学目标与数学核心能力适配性的案例研究

汪玲玲

摘 要：數学核心能力是数学课程标准所重点强调的教学总目标之核。但对于低年级小学生，核心能力的发展存在诸多困难。文章立足于低年段数学教学目标，从学生实际经验角度入手，引导学生在具有广度和深度的核心问题探索中，能主动联系现实生活，感受数学知识的价值、魅力和作用，让学生可以在活跃、生动、自主、自由的知识探索交流中，不断强化对数学知识问题的分析、解决能力。

关键词：教学目标;数学核心能力;能力适配

数学核心能力既是思维活动的表征，也是核心素养的本质体现，当学生作答填空题、应用题、口算题等各种题型时，会潜意识运用逻辑推理、数学运算、观察转化、空间想象等不同的思维能力分析解决问题。所以，掌握数学技能就意味着拥有数学能力，而解题时起到关键性、决定性的能力，也被称为核心能力。自新课程标准颁布和落实以来，小学数学课程逐步构建起了全新的教育体系和价值取向，其中，数学核心素养常被作为教学总目标揭示出来，但对于低年段学生而言，他们抽象逻辑思维刚步入起始发展阶段，解决问题时主要凭借具体形象的材料进行分析、推理。

一、低年段教学目标定位

《全日制义务教育数学课程标准（实验稿）》根据不同阶段学生的认知水平与心智特征，将教学目标划分为1～3年级、4～6年级、7～9年级三个学段，第一学段即低年段（1～3年级），又分别从知识技能、数学思考、问题解决、情感态度四个层面，提出了具体的目标与内容。

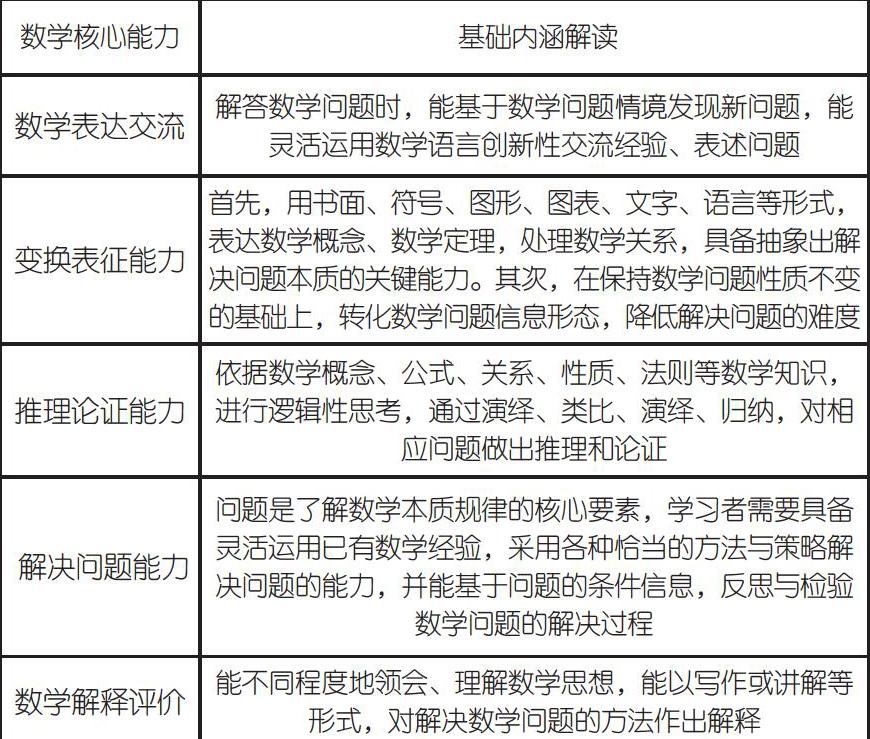
数学作为研究现实数量关系、变化与空间模型概念的学科知识，尤其注重对学生运算分析、数学抽象、逻辑推理能力的综合培养，但对于数学核心能力的界定，目前尚未形成统一明确的观点。综合国内外学者的不同观点可以发现，数学能力主要指学生完成学习活动过程中所具备的数学表达能力、交流能力、思考能力和判断能力。显然，拥有数学核心能力，意味着学生可以在各种不同的数学场景下理解、判断、表达、使用数学。因此，笔者基于国内外学者观点，从数学活动的主客体关系角度做出分析、评价，认为数学核心能力包括数学表征、推理论证、数学解释和问题解决能力。

可见，数学核心能力与核心素养间的基础内涵整体特征是相似的，而核心能力的实现，有赖于教学目标的落实和渗透。可以说，数学课程教学的本质目标和方法过程，决定着学生数学核心能力的构成。

因此，教师在数学课堂教学中，应围绕低年段教学目标，从学生实际经验角度入手，引导学生在具有广度和深度的核心问题探索中主动联系现实生活，感受数学知识的价值、魅力和作用，让学生可以在活跃、生动、自主、自由的知识探索交流中，不断强化对数学知识问题的分析、解决能力。以下笔者将从学生数学核心能力发展角度出发，以学生的认知特点和生活经验为着力点，进一步分析低年段教学目标与数学核心能力的适配性和相融性，以期使学生在有意义的自主建构中，学会全面、客观、辩证分析问题，理解数学本质思想，让学生能在生活化、新颖化的多样问题情境中，自主理解、判断和使用数学，实现逻辑推理、数学表达、问题解决等核心能力的全面发展。

二、结合现实经验，设计导思情境

例1：“两、三位数的加法和减法”

教师展示“课外跳绳比赛活动”情境内容，引导学生自主发现数学信息，并能根据已知条件发现问题、提出问题、解决问题。教师：“图中小红跳了多少下？你还会用哪些方法计算？”鼓励学生根据已知数学信息“45+23”转变逻辑思维，优化问题算法：“45+20=65 65+3=68;40+20=60 5+3=8 60+8=68。”教师：“哪种计算方法最好最快？”要求学生运用已掌握知识经验合作交流，发散思维能力，进行算法的优化。教师：“小满跳了多少下，小满比小红多跳多少下？应该怎样列式？”教师在恰当的时机，运用环环相扣、针对性强的问题，启发学生口算、笔算，通过算法的多样化，让学生自主体会如何在两位数加整十数，理解不同的问题在计算时有什么相同和有哪些不同，启发学生在两位数加一位数的分析、思考中，进一步深入识别已知条件和信息，提出两位数加两位数的算式和方案，理解进位加、不进位加两者之间在计算方法上区别与联系。

三、综合实践探究，表征转化交流

例2：“平移、旋转和轴对称”

教师：“同学们，物体在平移时，必须沿着直线运动，请看图说一说电梯和轮船的运动方式。”学生：“电梯沿着直线上下，轮船沿着直线航行。”教师：“物体沿直线从一个位置运动到另一个位置称为平移，我们生活中有很多平移现象，你能举出物体做平移运动的生活案例吗？”学生：“缆车、平拉抽屉、拉窗帘、升降机。”教师：“你想亲身体验一下平移吗？”指导学生结合生活实践和实例，感知体验平移现象，让学生在感受数学与生活联系的基础上，发展观察能力和空间想象能力。同时，“学会数学语言与他人合作交流”是数学课程目标之一，图像语言、符号语言、文字语言都是学生理解和学习的媒介。所以，教师在课堂中要基于教学目标，注重培养学生的空间观念、符号表征变换能力和数学交流能力，让学生能从现实生活中想象概括出几何图形，并通过几何体与图形之间的相互转化，由几何图形抽象出实物形状，能用数学语言清晰表达自己的思考体验过程。

因此，教师在数学课堂中，要融入丰富有趣的实践活动，鼓励学生利用原有数学活动经验和生活经验，亲自动手去做、动脑去想，经历观察、操作、验证、归纳、类比等活动过程，促使学生在交流、探究、分享中将数学经验和物体特征内化到自己思维中来。教师：“平行四边形、长方形、正方形是轴对称图形吗？请拿出一张长方形或正方形纸对折，尝试画出它的对称轴。”教师要鼓励学生亲自动手去做，让学生相互之间交流、展示不同的折法和画法，经历对称轴的探索过程。教师在教学中要配以提问，组织学生边思考、边实践、边交流折法，教师：“折纸时需要注意什么？长方形有几条对称轴？对称轴怎么画？你能画出几条对称轴？”指导学生在数学思考与问题解决中，发展空间观念和数学语言交流能力，持续加深对图形特征的认识。

教学目标决定和兼容了学生数学核心能力的构成，根据《数学课程标准（实验稿）》要求，低年段数学课程从知识技能、问题解决、情感态度三个层面，界定了新时期的目标追求和价值取向。因此，教师在课堂教学中，要始终坚持学生的数学核心能力发展目标 ，精准抓住课程改革引擎，让学生在生活化、多元化的问题思考探索中，经历从生活抽象出数的过程，循序渐进形成从数学角度聚焦问题、分析问题、探究问题解决方法的数学思维与核心能力。

参考文献

[1]吴正宪，孙佳威.数学关键能力的价值、内涵与培养路径[J].教学月刊（小学版数学），2020（04）：10-12.

[2]李小芹.有序思维促生长——小学低段学生数学有序思维能力培养的实践与思考[J].小学教学研究（理论版），2018（02）：23-24.