猕猴手指移动神经解码线性时不变模型的时间相关性研究

冯景义 吴海锋 曾玉

通过对神经回路感知外部世界和产生行为的研究,可揭示大脑的工作机制和规律,也可让人体增强感知外部世界和控制外部世界的能力.在神经编码中,例如,对听力障碍者来说,人工耳蜗可将声音信号编码为计算系统可处理的数字信号,通过刺激听觉神经使得患者具有感知外界声音的能力[1].在神经解码中,对于伤残人士来说,可直接通过大脑运动皮层的神经元峰电位数信号去操控外界设备的移动,如移动鼠标[2−3],机械手臂[4−5]等,以及截瘫患者的上肢和手[6]等,使其拥有一定的外部世界控制能力,目前康复机器人与智能辅助系统的研究取得了不错的进展[7].

神经编码将外部世界映射至脑活动[8],把从脑区获得的神经元峰电位信号进行分类处理,其处理后的峰电位信号需与肌肉或骨骼对外部世界产生的活动建立一一对应关系.神经解码是一种对神经编码的逆过程,从脑活动中解析出人体对外部世界的动作,例如,通过分类后的峰电位信号去预测或估计身体的运动过程,而本文所研究的猕猴手指移动位置估计是一个典型的神经编解码问题.首先完成神经编码,将神经记录仪器所采集的某一时刻猕猴运动皮层神经元峰电位数与该时刻猕猴手指移动位置建立对应关系.由于该问题已经在文献[9−14]中做了详细讨论,因此本文不再将其作为研究重点.其次完成神经解码,通过已经与猕猴手指移动建立对应关系的神经元峰电位数去估计猕猴手指移动位置信息,而本文的研究重点将集中在如何更好地解决神经解码问题上.

较早的猕猴手指移动的编码问题在文献[15]中进行了介绍,该文献发现猕猴的上部肢体的运动方向与其脑区的运动皮层中单个神经元的峰电位信号存在着相应关系;Vargas-Irwin 等实现了猕猴机器手臂的三维运动轨迹的重建,证实利用局部的神经集群发放信号可以解析出丰富的运动信息[16];O Doherty等在猕猴的初级感觉皮层上第一次实现了带有触觉反馈的闭环的脑机接口系统[17].在传统的解码方法中,较早采用的是独立线性(Linear)方法[18−19],该方法利用的是线性时不变模型(Timeinvariant linear model,TILM),将每一时刻运动状态值与该时刻记录的峰电位数信号看作时不变的正比关系,其最大优点是易于实施且计算简单,但缺点是把运动轨迹每一时刻的状态值均看成了一个独立过程,因此预测轨迹的准确度较低.

目前,为了解决该问题,常采用的方法是状态空间模型(State space model,SSM).在神经科学领域中,Velliste等通过SSM模型解码猕猴的运动皮层神经元峰电位数信号,实现了对四自由度假肢的控制[20];Shanechi等通过构建SSM模型和应用最优反馈控制模型解码出了猴子运动的轨迹状态[21];Chang 等基于卡尔曼滤波(Kalman-f ltering,KF)方法,设计出了同时考虑“手控”和“脑控”过程的算法,加快了脑控的实现[22].薛明龙等通过SSM模型,采用了一种无监督积分卡尔曼滤波解码模型(Unsupervised Cabuture-Kalman-f ltering decoding,UCKD)解码出了猕猴手指移动轨迹的位置[23−24];Hotson 等基于递归贝叶斯估计(Recursive Bayes estimation,RBE),通过整合环境传感器信息提高了脑机接口系统的解码效果[25].最近,浙江大学李宏宝还实现了猕猴手臂规避障碍过程中的运动前区皮层的神经解码[26],以及张毅等利用BRCSP(Bagging regularized common spatial pattern)算法实现左右手运动想象的脑电信号去控制智能轮椅完成了“8”字形路径实验[27].从SSM的观测方程看,仍是一种TILM模型,但同独立线性方法相比,SSM未把手指移动轨迹看成是一个时间上独立的过程,而是将当前时刻的移动状态与前一个时刻相关联,因此估计精确度有了较大提高.

本文通过对传统TILM模型的时间相关性进行研究,从SSM模型出发,将每一时刻的手指移动状态值与之前多个时刻的峰电位数的簇向量进行相关,推导出了另一种TILM模型.因为该模型是把猕猴手指移动轨迹的位置表示为一组神经元峰电位信号的簇向量与一组常系数的卷积,故称之为卷积空间模型(Convolutional space model,CSM).为了训练该模型,采用最小二乘和最陡梯度下降等常规方法来得到模型参数,同时分析了时间相关性对这些方法的影响.在实验中,采用一组公开的实测数据对本文的时间相关性问题进行验证,实验结果表明,CSM模型的训练算法所解码的手指移动位置信息要比传统的SSM模型有较小的解码误差.

1 相关工作

在猕猴手指移动神经解码中,SSM模型是目前较为流行的一种解码方法,其状态方程和观测方程可分别表示为[28−31]

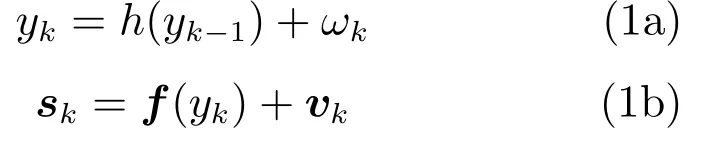
其中,yk为时刻k的手指移动位置信息,k=0,1,···,K−1,K为数据采样点长度,sk为Ne×1的列向量,表示为时刻k的Ne个电极上所采集的神经元峰电位数,h(·)表示状态方程函数,f(·)表示观测方程函数,ωk为零均值,方差为σ2的高斯白噪声[23],vk=[v0k,v1k,···,vNe−1,k]T是高斯白噪声矢量[23],其均值为0,方差矩阵Rv为对角线是的对角矩阵.

求解式(1)的状态空间方程通常采用逐次状态估计方法,可利用卡尔曼滤波(KF)[22,29],粒子滤波[8,28]和RBE[25]等方法.相比于将{yk,k=0,1,···,K−1}看作是独立的Linear 方法[8],与前一个状态相关的SSM模型所解码得出的手指移动轨迹曲线则更加平滑和抖动较小.

再者,SSM模型方法需要计算出该模型的h(·)和f(·)函数,一种常用的模型是将这些函数看作线性并利用训练数据得到,此时,式(1)变为

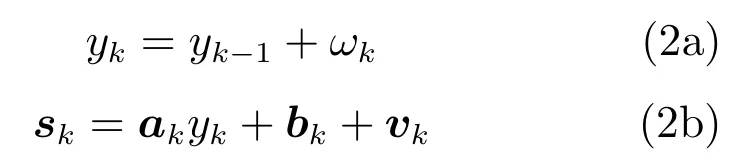
其中,ak,bk系数为Ne×1的列向量.由于该系数为时不变,故式(2b)可认为仍是一种TILM模型.另外,有人采用一种无监督的UCKD模型[23]把式(1)表示成了两组状态空间方程式,一组采用无监督算法来预测手指移动位置,另一组用来求解f(·)函数,其过程并未引入训练数据部分.

从以上基于式(1)∼(2)的SSM类方法看,其均认为当前时刻的手指移动位置状态yk仅与前一个时刻状态yk−1相关,在下一节中,我们将从时间相关性角度来分析SSM模型的合理性.

2 猕猴手指移动解码与时间相关性问题

猕猴手指移动位置的编解码过程,具体编解码过程如图1所示.在相关采集设备齐全的情况下,选用一只正常健康的猕猴,其手指能够自由运动的活动区域长为L,宽为B.

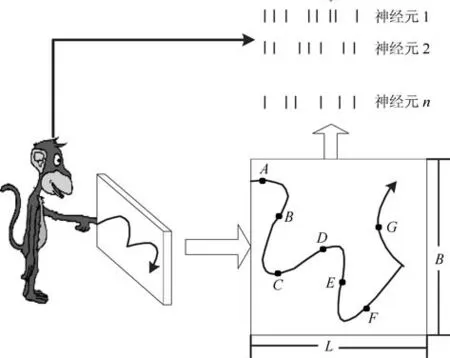
图1 猕猴手指移动轨迹编码Fig.1 Macaque finger movement track coding

首先,训练猕猴,在活动区域内会出现亮点作为目标物,不同时刻目标物出现在活动区域的不同位置,猕猴会用手指依次移向目标物,经过反复训练多次,最终猕猴能够独立地完成此项任务为止.其次,若目标物出现的周期为∆t,则在猕猴手部运动相关的活动脑区中植入的神经电极阵列将采集到第k∆t,k=0,1,···,K−1时刻的信息,即每一时刻的Ne个神经元峰电位数信号sk.然后,在每一时刻还需要记录猕猴手指移动的位置信息,如第k∆t时刻手指移动到A点,在记录神经元峰电位数信号sk的同时,也要记录手指移动到A点的X和Y轴坐标值yk,依次记录到B、C、D、E······的坐标位置值yk.最后,猕猴手指移动过程中共采集到了K组数据,即分别是K组神经元峰电位数信号sk和位置坐标yk具有相互对应关系.我们所要做的神经解码技术就是通过sk获取ˆyk,尽量使得估计ˆyk与真实yk达到一致.

从猕猴手指移动过程看,其移动位置轨迹{yk,k=0,1,···,K−1}应是一个连续过程,而基于SSM模型的传统解码方法仅将当前时刻的位置状态与前一个时刻的状态相关.其实,猕猴手指移动过程本身是一个具有一定速度和方向的连续过程,因此,其每个时刻的移动状态应该与以前若干个时刻的状态存在一定联系,若仅将当前时刻的状态与前一个时刻建立相关性,可能不一定是最优的.所以,本文尝试将当前时刻的运动状态与前若干个时刻的运动状态建立一定的联系,进而去寻找一种在时间相关性上更优的解码模型.

3 线性时不变模型的时间相关性研究

3.1 CSM模型

本小节将从时间相关性角度出发,将当前时刻的位置状态与之前若干个时刻相关,以克服SSM模型中描述手指移动轨迹连续性的不足.在该模型的推导中,将从SSM模型入手,得到了一种具有卷积形式的空间模型,其可以较为严格地确定和说明噪音的分布和特性.

假定本文模型中时刻k的位置状态yk与前P个时刻k,k−1,···,k−P+1相关,则由(2b)可得,在第k−p时刻的位置坐标

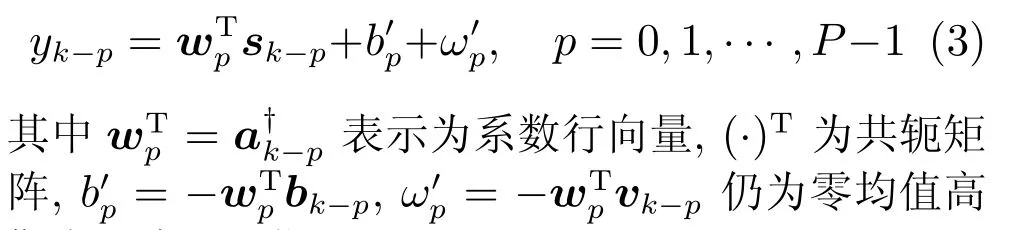
斯白噪声(见附录A).

将式(2a)代入(3)中,可得

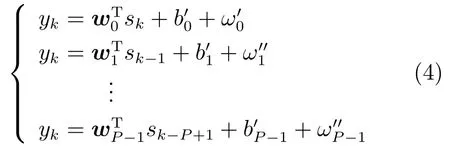
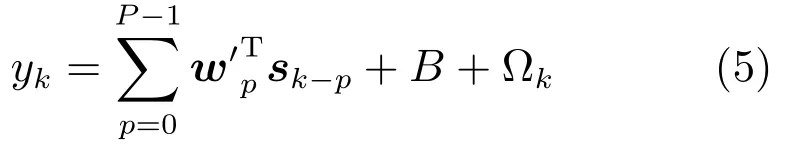
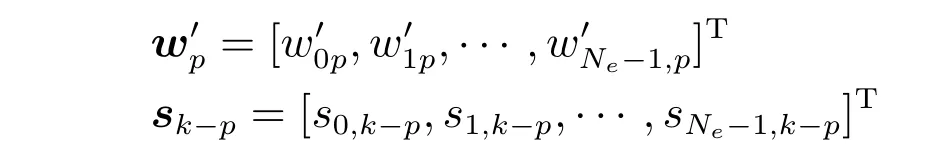
则有

式(6)表明了,运动状态位置信息yk是神经元峰电位数向量sk与权向量wk的二维卷积形式,见图2.从图2可看出,该二维卷积模型应该更加适合处理神经元峰电位数信号中的多维形式.

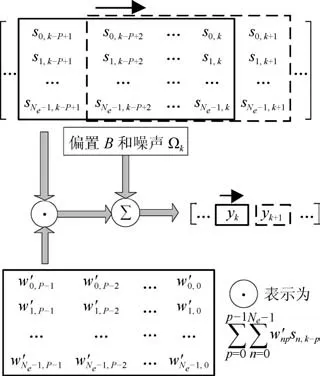
图2 二维卷积空间模型示意图Fig.2 Two dimensional convolution space model

进一步简化,令

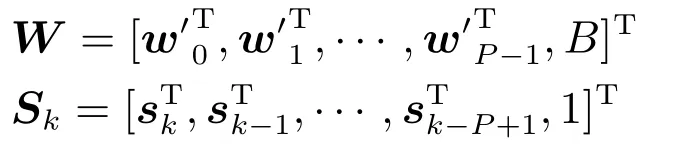
则有

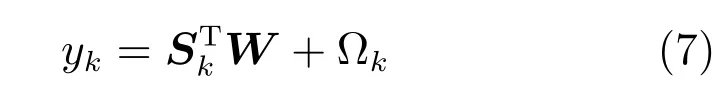
式(7)进一步表明运动状态位置yk是神经元峰电位数矩阵Sk与权矩阵W的内积并加上高斯白噪声Ωk.从式(6)∼(7)的卷积模型中看到,yk不仅与时刻k的峰电位sk相关,还与sk−P+1,sk−P+2,···,sk−1相关.另外,值得注意的是,模型中并没有考虑位置信息的时间相关性,yk并没有与yk−1,yk−2,···,等相关.

3.2 时间相关性对模型训练的影响

接下来,需要对前建立的模型进行训练,通过训练数据求解出模型的权值参数W.从第3.1节可知,CSM模型所解决的时间相关性问题,主要是引入的参数P将当前时刻的轨迹状态与前若干个时刻的状态变化建立了相关性.当P=1时,模型为时间独立的线性模型,故本节将重点分析和讨论参数P >1时,对该模型训练过程的影响.

3.2.1 时间相关性对训练方法的影响

在TILM模型中,若噪声为零均值高斯白噪声条件下,则可采用最小二乘法(Least squares,LS)和最陡梯度下降(Gradient descent algorithm,GDA)等训练该模型.由于CSM模型中出现的噪声都是高斯白噪声(附录A),故可采用LS,表示为[32]

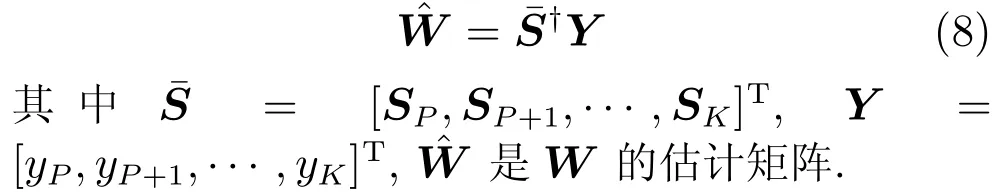
由于CSM模型的参数P >1,因此在LS算法中,式(8)中的观测矩阵¯S的列数将由原来的Ne+1变化为PNe+1.观测矩阵的维度变化将直接影响到模型训练的复杂度.

另外,可采用批处理的递归最小二乘法(Recursive Least Square,RLS)去训练CSM模型,表示为[32]

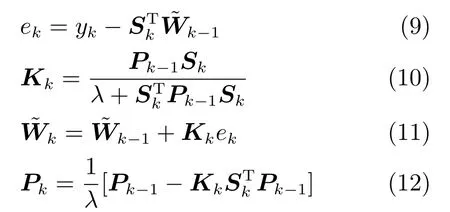
同样,(9)∼(12)中观测矩阵Sk的列数也由原来的Ne+1变化为PNe+1.

最后,梯度下降法(Gradient descent algorithm,GDA)同样是一种常用的批处理模型训练算法,表示为[32]

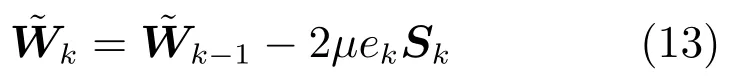
其中,µ是迭代步长.与RLS算法类似,其观测矩阵仍采用列数为PNe+1的矩阵Sk.

3.2.2 时间相关性对训练复杂度的影响

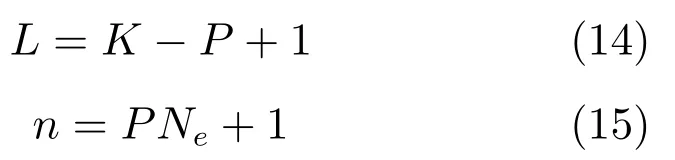
忽略低阶项和加减负项,LS关于参数P的计算复杂度可表示为O(P3).其次,RLS第k步的求解需要n3+2n2+n次乘除,总共要完成L步,如果需要T次循环才能达到收敛,那么RLS需要的乘除次数共为TL(n3+2n2+n),忽略低阶项和加减负项,因此RLS关于P的计算复杂度可表示为O(TP3).还有,GDA 第k步的求解需n2+2n次乘除,共需完成L步,如果共需T次循环才能达到收敛,那么GDA需要的乘除次数共为TL(n2+2n),因此GDA关于参数P的计算复杂度可表示为O(TP2).

表1给出了CSM模型训练关于参数P的计算复杂度,由于传统的时间独立模型中参数P=1,因此CSM模型的复杂度相比于传统模型的复杂度分别增加了P3,P3和P2倍.

表1 参数P 对算法的训练复杂度Table 1 Training complexity of parameter P for algorithm

3.2.3 时间相关性对训练参数的影响

在CSM模型中,所求卷积核W的参数个数为PNe+1,因此,相较于时间独立模型的参数个数,其增加了约P倍.

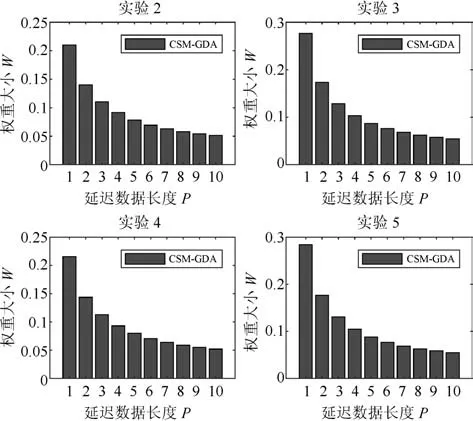
图3 时间相关性下卷积核权重大小分布Fig.3 Convolution kernel weight distribution in time correlation

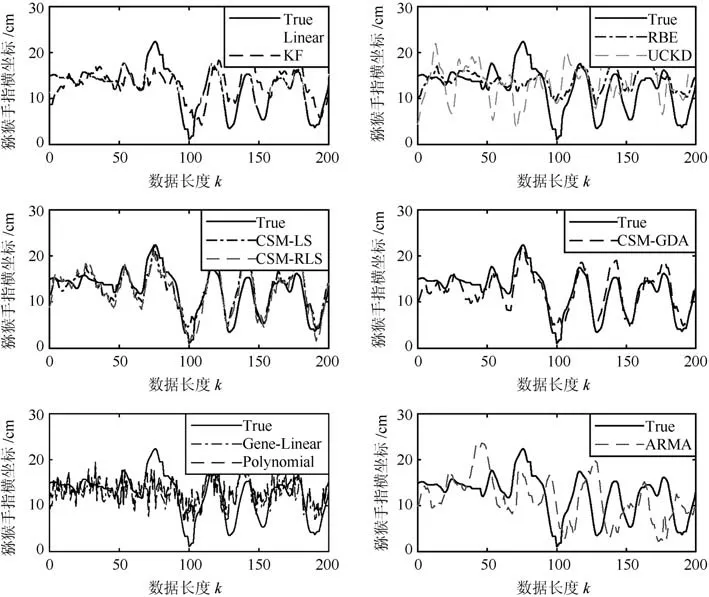
图4 实验1中位置估计与手指移动真实位置曲线Fig.4 Position estimation and finger movement real position curve in experiment 1

图3给出CSM模型在4组实验中的卷积核W训练结果,其中权重大小为p=1,2,···,P的2范数,P=10,训练方法采用GDA算法,4组实验的设置可参见第5.2节.从图中4 组实验的训练结果看,卷积核的大小随P的增大而逐步减小,这说明与当前时刻越接近的时刻相关性越强.另外,随着P的增大,卷积核权重下降逐渐趋于平缓,特别当P >10时,权重大小已降至0.05以下.该结果说明,P的取值并不是越大越好,因为随着P的增大,其权重对模型时间相关性的贡献已变得非常小.

4 神经解码

完成对CSM模型的训练以后,可将拟解码的神经元峰电位数信号代入到CSM模型中,继而解码出手指移动位置,如下给出了猕猴手指移动位置神经解码的完整算法.

算法1.估计yk的LS算法

算法2.批处理RLS算法

算法3.批处理梯度下降算法

5 实验结果与分析

5.1 数据来源

数据由Hatsopoulos实验室[8]提供,下载地址为http://booksite.elsevier.com/0780123838360,数据采集的具体过程可见第三部分编解码问题描述,其中相关参数值如下.

1)猕猴手指活动范围L=25 cm,B=18 cm.

2)猕猴脑部采集电极数Ne=42.

3)采样周期∆t=70 ms.

4)数据长度K=3 101.

所下载的数据共有两组,具体描述如下.

5)数据1:由二个数据矩阵组成,一个是K×Ne的神经元信号特征矩阵;另一个是K×2的坐标位置标签矩阵,其中标签矩阵的第一列为X轴,第二列为Y轴,活动范围为长L,宽B.

6)数据2:格式与数据1相同,同样由二个数据矩阵组成.

其中,数据1和数据2均在同等条件下采集.数据1和数据2的区别是,数据1中有方向随机的连续性手指移动,数据2中存在有水平或垂直方向维持一段时间的移动.

5.2 实验及参数设置

本实验将先后采用5组实验来评判神经解码的性能,对数据1和数据2的实验数据经处理分成5组实验如下.

实验1.对数据1采用验证方法为Holdout验证[33],70%的数据用于训练,30%的数据用于测试;

实验2.对数据1采用验证方法为M折交叉验证[33],其中M=10;

实验3.对数据2采用验证方法为M折交叉验证[33],其中M=10;

实验4.数据1作为训练数据,数据2作为测试数据;

实验5.数据2作为训练数据,数据1作为测试数据.

实验2和3的M折交叉验证中,误差评判标准采用均方根误差ec,定义如下

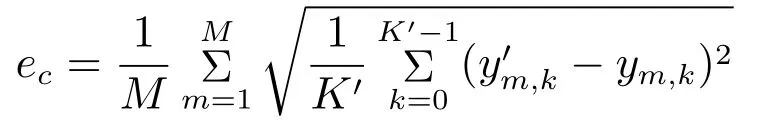
其中ym,k和ym,k分别是第m次交叉验证得到的解码值和真实值,K为交叉验证的数据长度.

实验4和5的误差评判标准采用er,定义如下

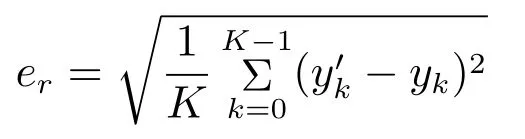
其中yk和yk分别是测试数据中解码值和真实值,K为测试数据的数据长度.分别采用均方根误差ec和er来评判解码方法在实验2至5的泛化能力.

在5组实验中,分别对Linear[8],KF[22,29],RBE[25],UCKD[23]和CSM模型方法计算出均方根误差ec和er,相关参数如下设置.

Linear:首先用最小二乘法训练式(3)的模型,然后利用测试数据解码移动轨迹位置.

RBE:X轴的估计区间为0.5:1:24.5(起始值是0.5,间隔是1,终点值是24.5),Y轴的估计区间为0.5:1:14.5.

CSM:除以上相关参数以外,还有,遗忘因子λ=0.9999,延迟的时间相关性数据长度P=10,RLS的迭代循环次数T是3,GDA迭代步长µ是2×10−6,GDA迭代循环次数T是60.

5.3 解码结果分析

图4给出了实验1中各算法对X轴轨迹解码的曲线图,并从所有测试数据中取200个样本点.从图中得出,对手指移动位置的轨迹基本都能跟踪上,当然,每种算法所表现的性能并不完全相同.Linear 算法解码的轨迹有较多的抖动和毛刺,如第80∼100点附近波动较频繁,主要原因是Linear把手指移动位置看成了一个独立过程,没有时间前后的相关性.UCKD算法偏离真实轨迹较大,如120∼130和150∼160点出现与真实轨迹反向的情况,导致误差较大,是因为该算法采用的是无监督解码,再者,该算法解码X轴时,轨迹的正反向有时未能辨识,但是,对Y轴有较好的辨识度[23].采用SSM模型的算法是KF和RBE,解码曲线较为平滑,抖动较小,原因是SSM模型把当前时刻的状态与前一时刻有了相关性,但有时解码曲线未能完全反映实际曲线的变化趋势,如出现急速转向的40∼60点附近.本文采用CSM模型的LS、RLS和GDA算法,对趋势反转处仍能较好跟踪上真实轨迹,如20∼40,40∼60和80∼100等,该结果表明当前时刻的状态的确与前若干个时刻的状态有相关性.另外,图4还分别给出了传统TILM模型在X轴解码的曲线图,从图中可以看出,广义线性(Generalized linear model,GLM)、二次多项式(Polynomial)、自回归滑动平均(Auto-regressive moving average model,ARMA)三种模型在细节部分总是存在毛刺或抖动情况,导致总的估计性能较差.

以上是定性分析,下面给出定量分析.表2给出各算法对实验2至实验5中X轴的解码误差,其中实验2和3的误差计算是ec值,实验4和5的误差计算是er.4组实验的误差均值由高到低分别为UCKD、Linear、RBE、KF、GDA、LS和RLS,其中RLS算法相比误差最小的传统KF算法,减小约11.1%.另外,分析每一组实验的均方误差,采用CSM模型的算法都会小于或接近于传统算法的误差,其中在实验4中GDA的误差为4.58 cm,高于传统算法,说明GDA处理这组数据的泛化能力较弱.

另外,表2还给出Y轴中各算法的解码误差,4组实验结果的误差均值从高到低依次是UCKD、Linear、RBE、LS、RLS、KF和GDA,此次KF算法误差值都略微低于LS、RLS算法约0.02 cm,但误差值最小的仍然是CSM模型的算法.并且,对于每组实验,采用CSM模型的算法的均方误差同样小于或接近于传统算法.只是,GDA算法相比误差最小的传统KF算法,均方误差仅减小约5.3%,不如X轴的性能提升.需注意的是,Y轴的泛化能力强于X轴,主要原因是Y轴的测试数据和训练数据集的相似度更高.最后,表3给出二维平面中各算法的解码误差,与表2类似,误差均值最小的仍是采用CSM模型的算法.

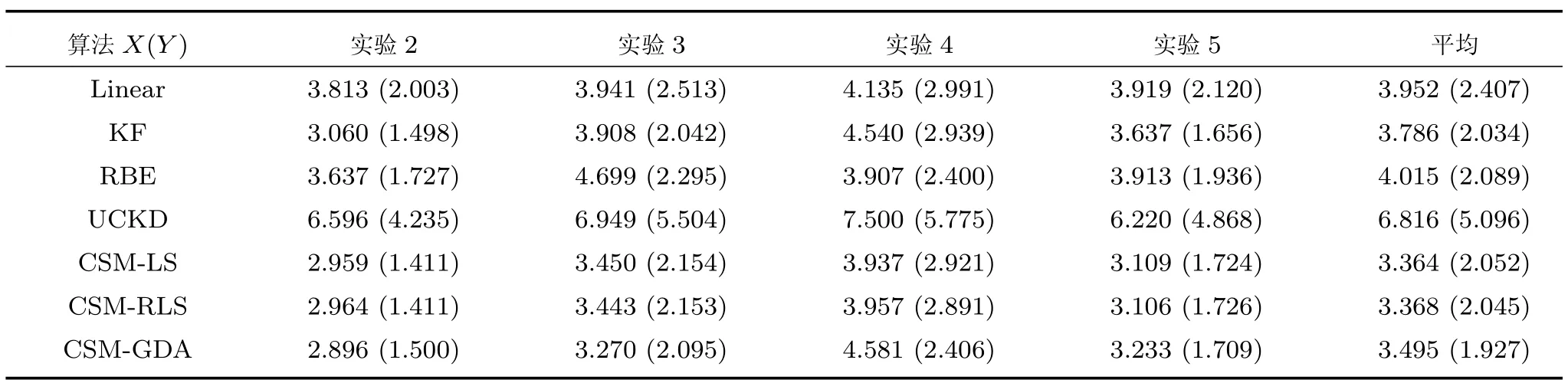
表2 X 轴和Y 轴(括号内)的估计误差(cm)(保留三位)Table 2 X-axis and Y-axis(in parentheses)estimated error(cm)(three places reserved)

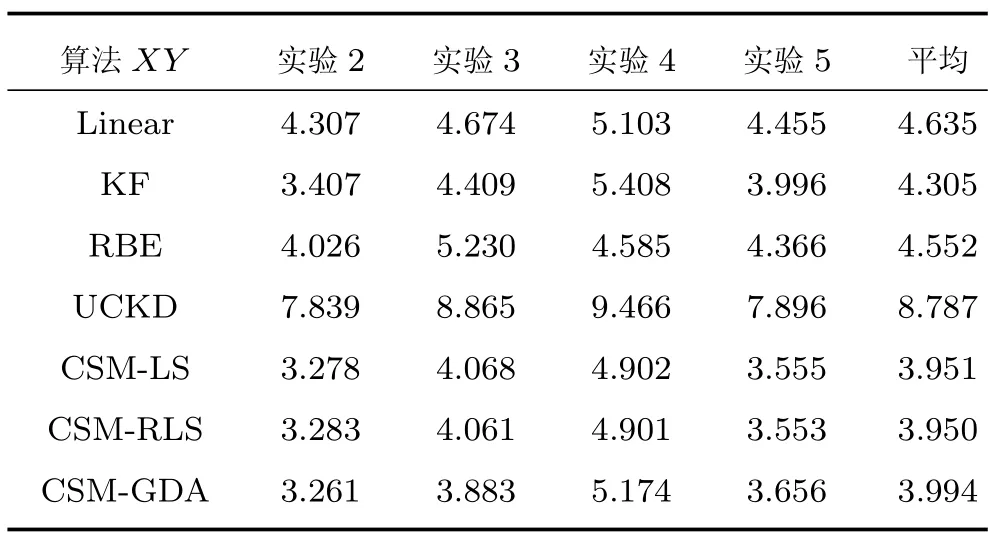
表3 二维平面的估计误差(cm)(保留三位)Table 3 The estimated error of the two-dimensional plane(cm)(three places reserved)

图5给出CSM模型中P值对解码性能的影响,分别给出了实验2到5中LS、RLS和GDA的均方误差曲线变化图.从图中看出,LS和RLS算法的误差曲线几乎处于重合,在约P=20以后,误差曲线呈增长趋势.再者,在实验2、实验3和实验5中,采用CSM模型的LS、RLS和GDA在参数P=10以前的误差曲线均下降,直到约3 cm左右,然后趋于稳定,最后在P=20时又呈增大趋势.在实验4中,GDA的误差曲线是先减小后增大,再减小后趋于稳定,而LS和RLS是先增大后稳定再增大趋势,但在约P=10时它们都会处于较小误差.原因是当P过小出现欠拟合,当P过大出现过拟合,此时有较差的泛化能力.因此,当P=10时采用CSM模型的算法解码手指移动位置能保证有较小误差.

图6给出在CSM模型中循环迭代次数T值的实验结果,分别给出RLS和GDA算法的均方误差曲线图.从图中看出,GDA算法的误差曲线随着循环迭代次数的增加,直到T=10左右,呈快速下降,随后下降趋势减缓,最后在约T=40以后,误差曲线就会趋于稳定状态.另一方面,RLS算法的误差曲线随着循环迭代次数的增加,不能保证误差曲线下降.从分析中得出,采用CSM模型的GDA,循环迭代次数可最低设置T=40,因为之后的误差曲线并不会再下降.还有,采用CSM模型的RLS算法,由于误差曲线变化不明显,故可不循环迭代或较少的循环迭代次数.

最后,为了评估CSM模型中三种算法的计算复杂度,表4给出了其在实验4中的训练时间,其中RLS算法的循环迭代次数T=3,GDA 算法的T=60.PC电脑操作系统为Windows 7 旗舰版64位SP1,处理器为英特尔Corei5-6400 2.70 GHz四核,处理软件为MATLAB R2017b.从表4可以看出,RLS算法运行时间最长,GDA算法次之,LS算法运行时间最短,该实验结果与第3.2.2节一致.

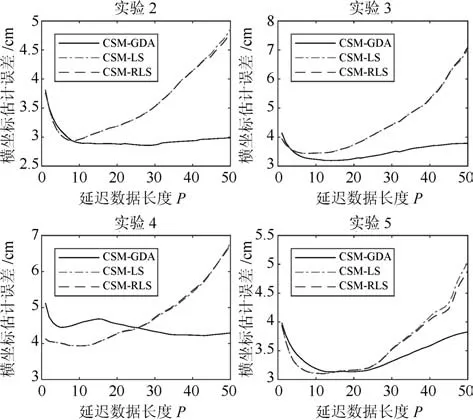
图5 手指移动横坐标估计误差随延迟数据长度P 的变化Fig.5 Finger movement abscissa estimation error with delay data length P changes

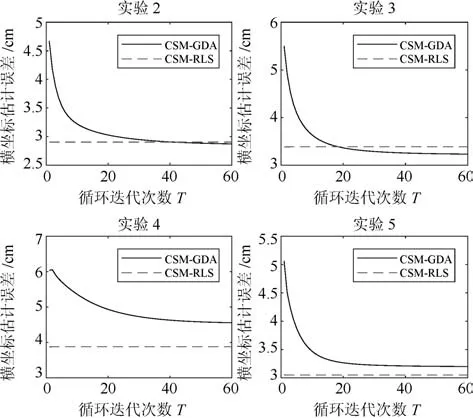
图6 手指移动横坐标估计误差随迭代次数T 的变化Fig.6 Finger movement abscissa estimation error with the number of iterations cycle T changes

表4 CSM模型算法的训练时间(保留三位)Table 4 The training time of CSM model algorithm(three places reserved)

6 讨论

本文通过对手指移动位置解码模型的时间相关性研究,采用了CSM模型来解码手指移动位置的方法,并采用了三种算法来训练模型.与传统模型的解码结果相比,其解码结果的误差有所降低.但是,对于CSM模型和训练方法还有以下几点需要进一步进行讨论.

首先,对时间相关性分析后,引入了参数P使得需要训练的参数数量增多.在传统SSM模型(2)中训练的权值a和偏执b的数量为2Ne,在CSM模型中该数量变为PNe+1.由于增加了训练参数,使得训练算法的复杂度增加.但是,解码中只是增加算法的乘法步骤,故训练复杂度对解码影响不大.

再次,参数P的确定会对解码性能产生重要影响.若P选择过大会产生过拟合,选择过小会欠拟合使误差增大.为确定P的合适值,可在解码之前,再设置一个验证集,以便确定最合适的P值.

另外,从实验数据也可以看到,本文的CSM模型虽然主要性能在X轴而非Y轴,但是对二维平面解码的误差性能也有较大改善.

除此之外,对于批处理的训练方法,RLS和GDA算法需要一定的循环迭代次数.从实验结果看,RLS一次循环结果和多次循环结果性能接近,因此循环次数可设置1.对于GDA算法,循环迭代次数需40次以上才能达到收敛,增加了计算复杂度.然而,由于前10次循环中GDA的误差就迅速下降,虽然后续的循环仍有所下降但已趋向平缓,因此,为减少循环时间,不一定要将循环次数设置至收敛时,T=10次循环是一个可行的选择.而且,参数P对GDA算法的计算复杂度影响为O(TP2),相比于其余两种算法的O(P3)和O(TP2),增加T的值有时并不一定会增加过多的复杂度.

需要注意的是,本文的CSM模型方法本质上仍然是一种有监督的解码方法,因为算法的解码离不开训练数据集.其实,人类的学习过程就是一种无监督,其可以不依赖于训练标签就可解码出手指移动轨迹,更符合实际的学习方法.虽然UCKD方法是一种无监督方法,但令人遗憾的是,它对于X轴的解码效果并不理想.另外,还可以考虑半监督或弱监督的解码方法,即使训练集合的标签信息不完整也能解码出位置信息,例如仅知道手指移动位置的大概信息而不是确切信息,这些都可以是以后的一个研究方向.

最后,CSM模型本身是一个卷积模型,将近来较为流行的深度卷积神经网络(Convolutional neural network,CNN)来进行学习,从初步试验结果看能够大体跟踪上运动趋势,然而仍然有一些问题还需解决,例如网络参数设置、初始化和激活函数等问题.再者,目前深度网络中会引入非线性激活函数,同时时间不变线性模型与递归神经网络(Recurrent neural network,RNN)有相关性,可以考虑把这些特性或方法与本文卷积空间模型进行结合.需要注意的是,文中卷积空间模型重点是对输入多维数据的处理,故可以采用各种算法解决此模型中多维数据的问题,而递归神经网络本身是可直接调用的算法层面.神经元峰电位数信号中究竟有哪些特征能够真正影响手指移动位置解码,这一点并没有一个公认的答案,而深度卷积神经网络具备自动学习提取目标对象的特征值,这提供了一个解决本问题可尝试的方向.例如,是否可以尝试把本文的解码回归问题转化为分类问题,因为深度卷积网络更多的应用场合是分类,这会是一个新的思路.经过我们的初步实验,神经网络方面算法处理本文的回归问题,导致M折交叉验证中每次循环迭代产生的估计结果不稳定性很高.故我们认为,在后续的研究中,如果此回归问题转化为分类问题得到解决,可采用CNN,RNN等神经网络算法做更深入的分析.

7 结束语

本文中神经解码就是通过猕猴运动皮层的神经元峰电位信号预测其手指移动位置.分析了传统解码模型的时间相关性问题,采用一种具有卷积形式的线性时不变模型,称为CSM模型.然后,采用CSM模型的LS、RLS和GDA算法去训练模型的权值参数,最后去解码出手指移动轨迹.本文采用的模型使猕猴当前时刻的状态与前若干个时刻的峰电位数有相关性,将手指移动位置表示为神经元峰电位数的簇向量与一组常系数的卷积.

CSM模型中,P=1时,模型是时间独立的线性模型,P >1时,是卷积空间模型.另外,CSM为二维卷积,可用来处理输入多维神经元峰电位数信号.再者,该模型主要是针对神经元峰电位数信号的时间相关性,并未考虑手指移动位置的时间相关性.

在实验中,利用公开数据,分别采用Holdout和交叉验证给出了5组实验结果,来评判本文方法的解码性能.从实验结果来看,与传统方法相比,本文方法在对X轴解码的误差均值上有了约11.1%的性能提升.另外,实验结果还证实,CSM模型中当前时刻的状态与前10个时刻的状态具有较好的时间相关性,解码误差较小.最后,从实验结果来看,采用CSM模型的RLS和GDA算法都采用了循环迭代,其RLS算法至少一次循环迭代就能达到收敛,GDA算法的循环迭代次数较多.

附录A 高斯白噪声证明

由式(3)可知