带未知模型参数和衰减观测率系统自校正分布式融合估计
2021-04-18段广全孙书利
段广全 孙书利
近年来,多传感器信息融合技术得到广泛关注.经典Kalman滤波需要已知模型参数和噪声统计特性[1].而在实际应用中,系统可能会出现模型参数或噪声统计特性未知情况.文献[2−4]研究了带未知噪声方差系统的自校正估计问题.文献[5]和[6]研究了模型参数和噪声方差未知系统的自校正融合估计问题.文献[7]针对带未知模型参数和噪声统计特性且噪声相关的多传感器系统,分别应用RELS算法、Gevers-Wouters算法对未知模型参数和噪声统计特性进行辨识,并提出了自校正融合估值器.文献[5−7]中在对未知模型参数进行融合处理时,采用加权平均方法获得最终融合辨识器.该方法没有考虑不同传感器的局部参数辨识的差异,不能保证融合后的参数估计精度都优于每个局部参数估计.上述文献所提出的辨识和估计算法都是基于完整的传感器观测数据,而没有考虑数据的不完整现象.
在实际的网络化系统或传感器网络中,由于传感器老化或故障、以及传感器的观测数据在通信传输过程中由于带宽有限,可能会出现数据丢失、衰减、延迟等问题,使得估值器所收到的传感器数据具有不完整现象[8].文献[9]研究了带多丢包系统的最优估计问题.文献[10]将文献[9]的单传感器系统推广到了多传感器系统,对带有不同丢包率的多传感器系统,提出了集中式和分布式融合估值器.文献[11−14]考虑数据在传输过程中存在的丢失和延迟现象,设计了相应的最优估值器.其中文献[13]在文献[12]的基础上研究了带随机乘性噪声、多丢包和滞后系统的最优估计问题.文献[14]考虑了过程噪声和观测噪声具有一步自相关和互相关的情况.文献[15]和[16]对带有数据包丢失的多传感器系统,应用协方差信息方法设计了分布式融合估值器.在上述文献[9−17]中数据丢失现象均由一组满足伯努利分布的随机变量所描述,这种数据丢失可以看作是观测数据发生衰减现象的一种特殊情况.文献[18]和[19]考虑了带随机参数矩阵、相关噪声和衰减观测系统的最优和次优估计问题.文献[20]中研究了带衰减观测系统的Kalman 滤波估计问题,同时分析了误差协方差的有界性和稳态特性.文献[21−22]对带衰减观测的随机不确定系统,分别设计了多传感器分布式和序贯融合估值器.上述文献都是在假设观测丢失率或衰减率已知的情况下得到的最优估计结果.而没有考虑观测丢失率或衰减率未知的自校正估计问题.目前,有关同时考虑带有未知模型参数和未知衰减观测率多传感器系统的自校正融合估计问题的报导甚少.
基于以上文献分析,本文将对带有未知模型参数和衰减观测率的多传感器随机系统,应用相关函数和递推增广最小二乘算法,分别在线辨识衰减观测的数学期望、方差和模型参数.应用线性无偏最小方差估计准则,分别提出了分布式模型参数融合辨识器和自校正融合状态滤波器,并分析算法的收敛性.
1 问题阐述
考虑带衰减观测的多传感器随机系统
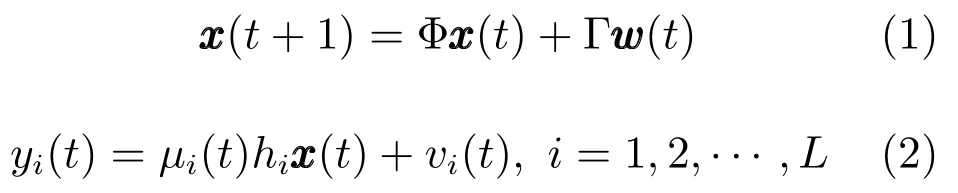
其中状态x(t)∈Rn,观测yi(t)∈R,过程噪声www(t)∈Rr,观测噪声vi(t)∈R,下标i表示第i个传感器,L表示传感器的个数.{µi(t)}为一组在[0,1]区间取值的用来描述第i个传感器衰减观测现象的标量随机变量.其中E[µi(t)]=αi,Cov[µi(t)]=E为数学期望符号,Cov 为协方差符号.{µi(t)}与其他随机变量不相关.Φ,Γ,hi是适当维数矩阵.
假设1.www(t)和vi(t)为零均值、方差阵分别为Qw和Qvi的不相关白噪声.
假设2.初值x(0)不相关于w(t)和vi(t),且E{x(0)}=u0,E [x(0)−u0][x(0)−u0]T=P0.其中T为转置号.
假设3.Φ为稳定矩阵,(Φ,hi)是完全可观对,(Φ,Γ)是完全可控对.
假设4.Φ中部分参数未知,{µi(t)}的数学期望αi和方差未知.
问题是基于观测(yi(1),···,yi(t)),i=1,2,···,L,辨识Φ中未知参数、{µi(t)}的数学期望αi和方差并求Φ中未知参数的融合辨识器和状态x(t)的自校正融合滤波器
注1.为了阅读方便,这里对后文中经常遇到一些术语给予解释.局部滤波器,即基于单个传感器的观测数据所获得的滤波器;最优滤波器,即系统的模型参数以及衰减观测期望和方差已知情况下,获得的线性最小方差意义下的滤波器;自校正滤波器,即系统模型含有未知参数,以及衰减观测期望和方差未知情况下,通过辨识这些未知参数,然后代入最优滤波算法中获得的滤波器.分布式融合滤波器,即基于各个传感器的局部滤波器,应用线性无偏最小方差矩阵加权融合估计算法[23]获得的融合滤波器.
2 分布式最优融合滤波
当系统模型参数、{µi(t)}的数学期望αi和方差已知时,应用线性无偏最小方差意义下的矩阵加权融合估计算法[23]可获得分布式最优融合滤波器.下面给出实现过程.
由式(2)可得
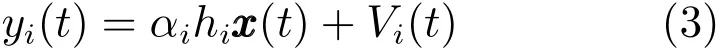
其中
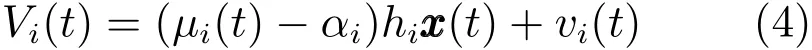
可计算其方差阵为

状态二阶矩X(t)=E[x(t)xT(t)]可递推计算如下:
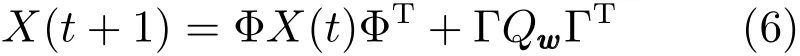
下面引理1 给出了最优局部滤波器算法;引理2给出了互协方差计算公式;引理3给出了分布式最优加权融合滤波算法.
引理1[24].在假设1∼3 下,随机系统(1)和(3)基于每个传感器的观测有最优局部滤波器
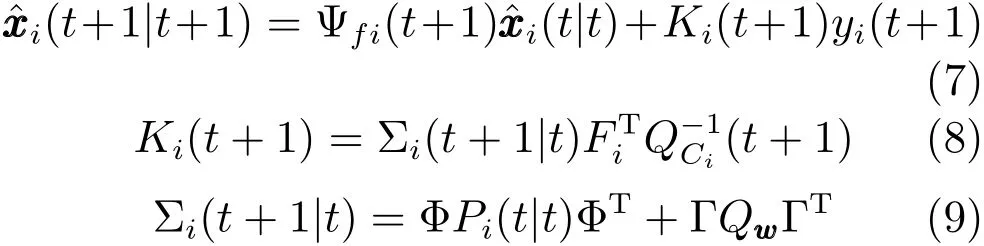
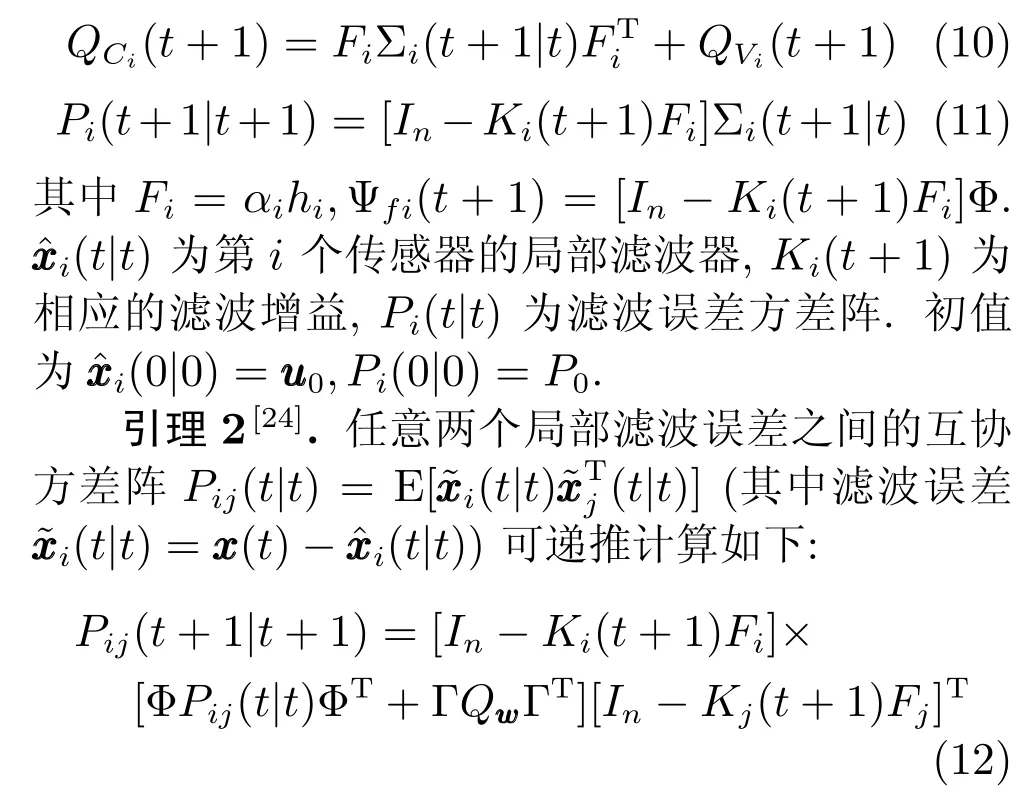
初值为Pij(0|0)=P0.
引理3[23].基于引理1的各局部滤波器和引理2的任意两个局部滤波误差之间的互协方差阵,分布式最优矩阵加权融合滤波器可计算如下:
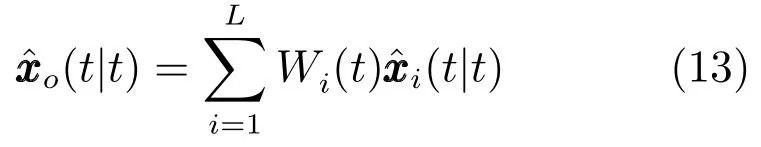
加权矩阵计算为
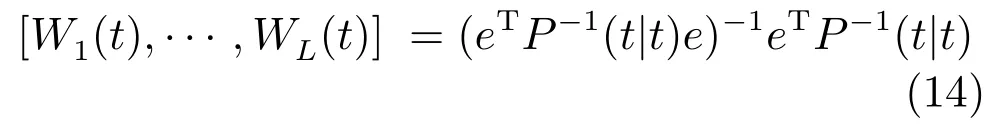
其中e=[In,···,In]T,P(t|t)=[Pij(t|t)]nL×nL是以Pij(t|t)为第(i,j)元素的分块矩阵.融合滤波器的估计误差方差阵计算为
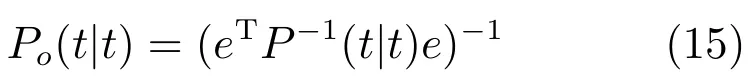
且有Po(t|t)≤Pi(t|t),i=1,···,L.
3 未知模型参数融合辨识器
上一节我们针对系统模型精确已知时给出了分布式最优融合估计算法.而在实际应用中,系统模型可能含有未知参数.当Φ中含有未知参数时,本节采用RELS算法辨识未知模型参数,并对辨识得到的L组参数估值进行加权融合,获得模型参数的分布式融合辨识器.下面给出具体实现过程.
由式(1)可得
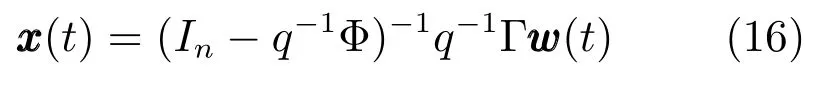
式中q−1为单位滞后算子,即q−1x(t)=x(t−1).将式(16)代入式(3)得

将式(17)进一步化简得
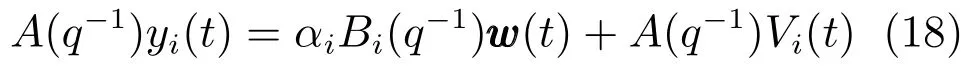
其中A(q−1)=det(In−q−1Φ),Bi(q−1)=hiadj(In−q−1Φ)q−1Γ,式中det和adj分别表示矩阵行列式和伴随矩阵.A(q−1)和Bi(q−1)具有如下多项式形式:
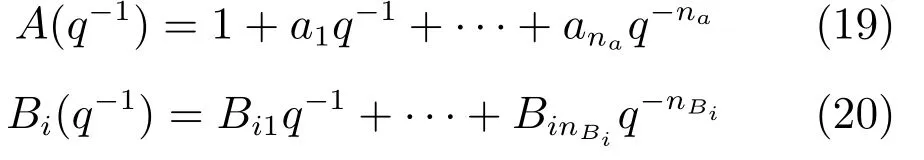
其中ak,k=1,···,na和Bik,k=1,···,nBi是多项式系数.nA,nBi分别为A(q−1)和Bi(q−1)的阶次.式(18)等号右侧两个滑动平均过程可以等价为一个稳定的滑动平均过程Di(q−1)εi(t)[24],即
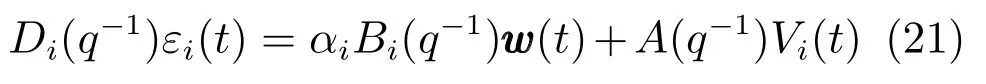
其中εi(t)是零均值且带有未知噪声方差σ2εi的白噪声,Di(q−1)具有如下多项式形式:
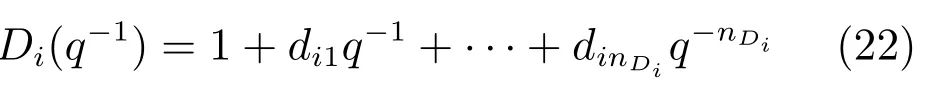
其中dik,k=1,···,nDi是多项式Di(q−1)的系数,nDi是Di(q−1)的阶次.
将式(18)重写为
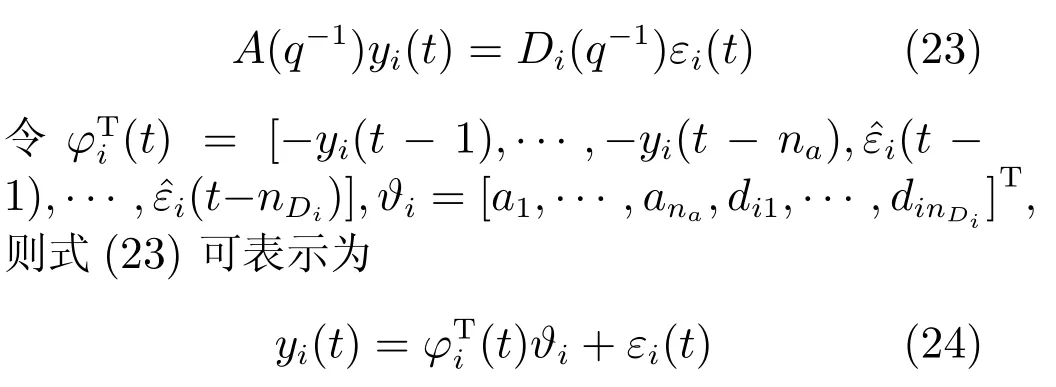
参数ak,k=1,···,na;dik,k=1,···,nDi未知.
基于每个单传感器的观测数据,应用RELS算法[24]可得到局部参数估计为
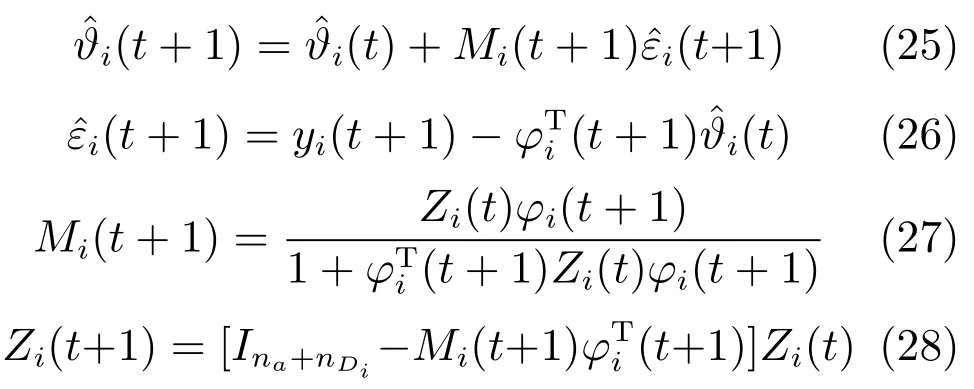

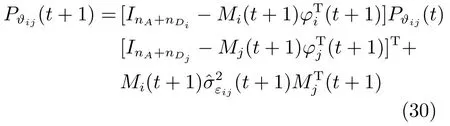
当i=j时,Pϑii(t)即为局部参数估计误差方差阵Pϑi(t).εi(t)与εj(t)之间的互协方差可近似计算如下:
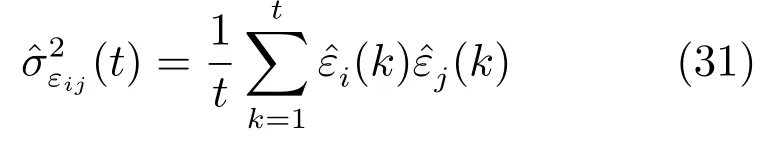
它可递推地计算为
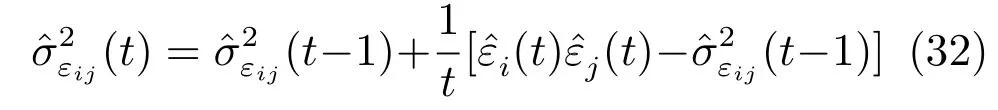
令ϑA=[a1,···,ana]T,则有ϑAi=[Ina,0]ϑi.于是,我们有参数ϑA基于传感器i的局部估计和估计误差协方差阵如下:
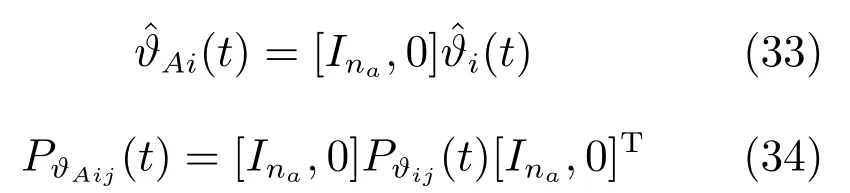
当i=j时,PϑAii(t)即为局部参数ϑA的估计误差方差阵PϑAi(t).
由式(18)可知,参数ϑA=[a1,···,ana]T是Φ中未知参数的函数.假设Φ中未知模型参数组成的列向量为Λ[Φ]∈RnΦ,nΦ≤na,且可由ϑA唯一确定.设Λ[Φ]与ϑA之间满足如下关系:

其中f(ϑA)为关于ϑA的线性或非线性函数.
1)如果f(ϑA)是线性函数,我们将式(35)重写为
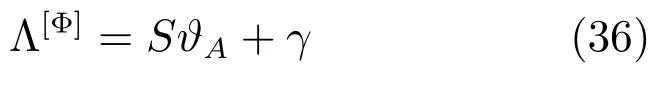
式中S,γ为适当维数的系数阵.
那么,基于传感器i的数据获得的Φ中未知模型参数在t时刻的局部估计为
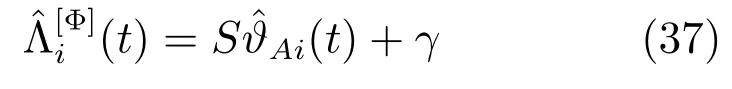


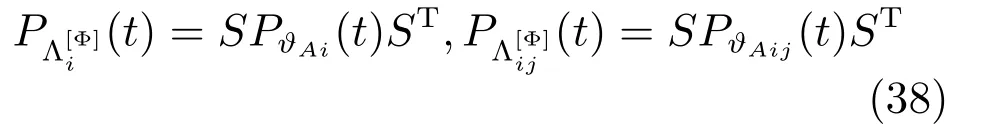
2)如果f(ϑA)是非线性函数,我们将f(ϑA)在点处进行线性化,有
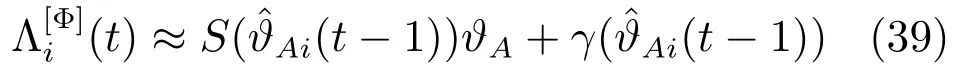
那么,基于传感器i的数据获得的Φ中未知模型参数在t时刻的局部估计为
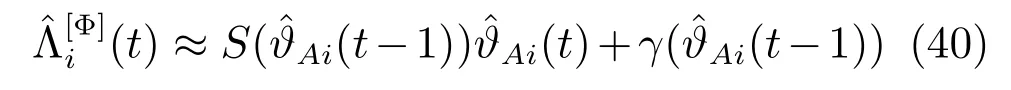
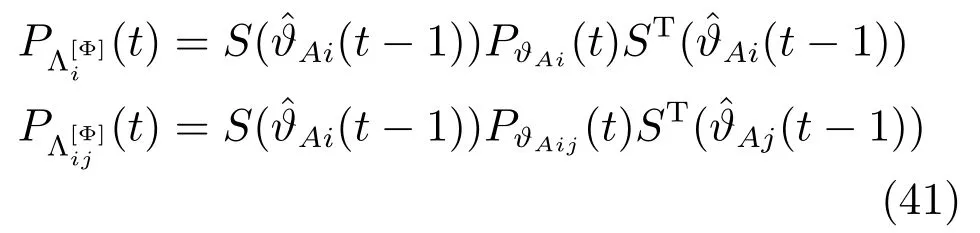
其中i,j=1,···,L.通过以上算法,基于L个传感器的数据可获得Φ中未知参数在时刻t处的局部估值i,j=1,···,L.由于对Φ中未知参数估计了L次,因此我们可应用线性无偏最小方差加权融合估计算法[23]将它们进行融合处理.下面定理1给出了未知参数分布式融合估计的结果.
定理1.基于局部参数估计局部参数估计误差方差阵以及参数估计误差互协方差可得在线性无偏最小方差意义下的矩阵加权参数融合辨识器如下:

参数融合加权矩阵计算为
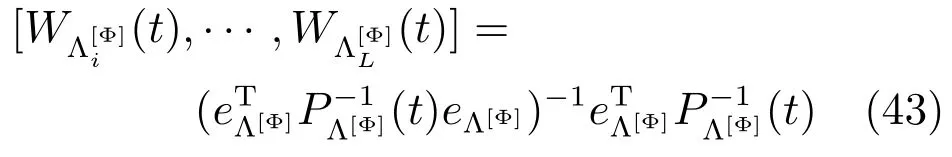

参数融合辨识器的估计误差方差阵计算为

注2.文献[5−7,24]在进行模型参数融合辨识时,将各传感器辨识得到的模型参数采用加权平均方法进行融合处理.该方法不能保证所获得的参数融合辨识器的估计精度不低于所有的局部参数估计.而本文采用线性无偏最小方差分布式矩阵加权融合算法[23]对各传感器辨识得到的参数进行融合处理.所获得的参数融合辨识器的估计精度不低于所有的局部参数估计.因此,本文的矩阵加权融合的参数估计精度高于加权平均融合的参数估计精度.这在后面的仿真研究中也能看到.
4 µµi(t)的数学期望与方差辨识
当各传感器的衰减观测率未知时,为了能应用第2节中的算法获得状态估计,我们需要辨识描述衰减观测的随机变量{µi(t)}的均值和方差.下面我们采用相关函数来辨识它们.
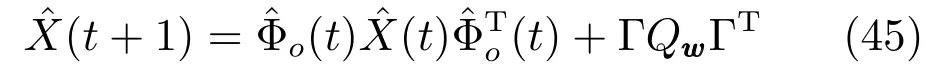
由式(2)可计算零步相关函数Ri(t,0)=E[y2i(t)]为
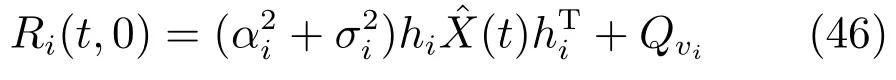
一步相关函数Ri(t,1)=E[yi(t)yi(t−1)]为
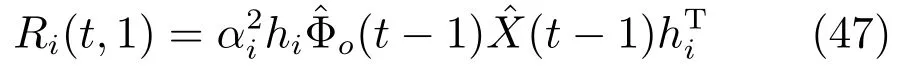
零阶和一阶相关函数阵Ri(t,r),r=0,1可通过如下采样相关函数逼近:
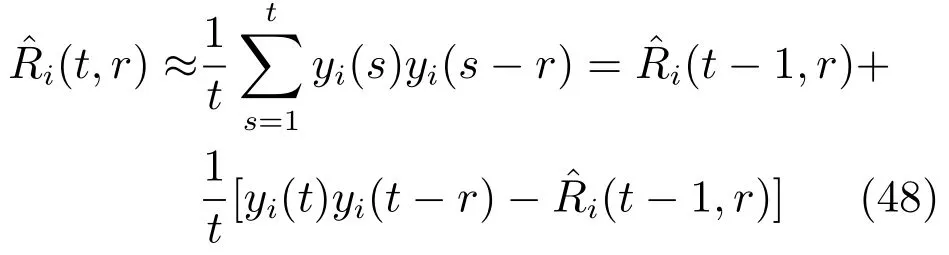
最后,由式(47)可求出随机变量{µi(t)}的数学期望为
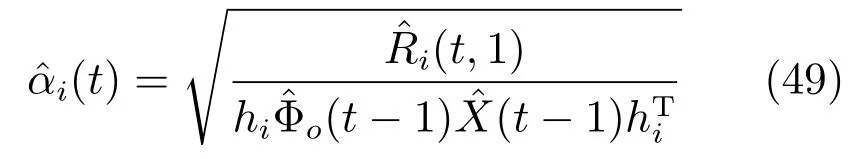
将式(49)代入式(46)可得随机变量{µi(t)}的方差为
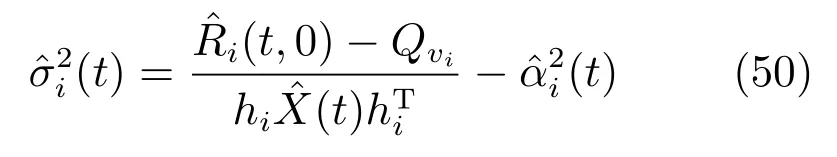

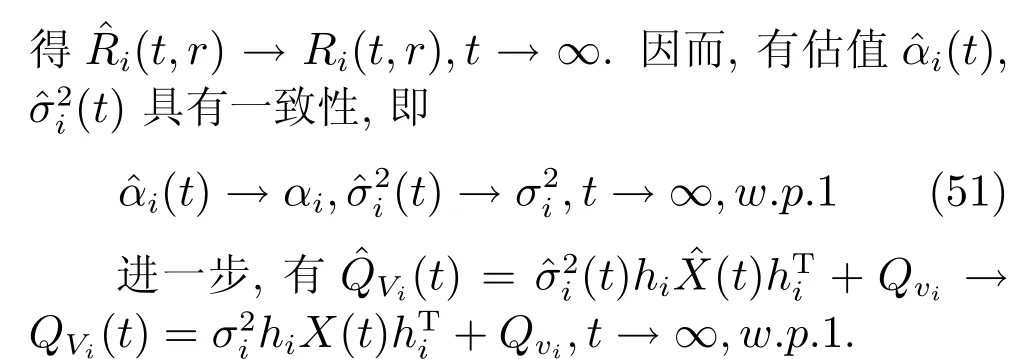
5 自校正滤波器的收敛性分析
下面的引理4给出了DESA方法,应用DESA方法可证明自校正融合状态滤波器的收敛性.
引理4[24].考虑动态误差系统
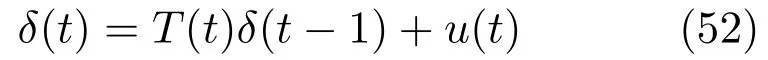
其中t≥0,输出δ(t)∈Rn,输入u(t)∈Rn,并且矩阵T(t)∈Rn×n是一致渐近稳定的.若u(t)是有界的,则δ(t)是有界的.当t→∞时,若u(t)→0,则δ(t)→0.

定理2.在假设1∼4下,自校正局部滤波器收敛于最优局部滤波器即
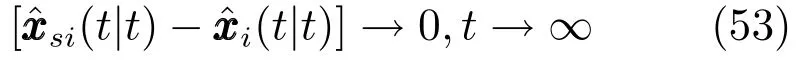
证明.由式(7)可得自校正滤波器为



6 仿真例子

在仿真中假设未知模型参数a11=0.6,a12=−0.2,µi(t),i=1,2,3,的概率分布分别为P{µ1(t)=0.3}=0.3,P{µ1(t)=0.5}=0.2,P{µ1(t)=1}=0.5,P{µ2(t)=0.4}=0.4,P{µ2(t)=0.7}=0.3,P{µ2(t)=0.9}=0.3,P{µ3(t)=0.1}=0.2,P{µ3(t)=0.6}=0.6,P{µ3(t)=0.9}=0.2.我们可以计算µi(t),i=1,2,3的数学期望和方差分别为
为了与文献[5−7,24]中的参数加权平均融合算法相比较.如下给出了模型参数a11和a12的局部估计误差方差、加权平均估计误差方差以及分布式加权融合估计误差方差算法.
a)局部参数估计和分布式加权融合估计:
根据前面的第3节,可知未知模型参数与ϑA=[a1,a2]T有如下线性关系


b)参数的加权平均融合估计:
Λ[Φ]的加权平均估值为
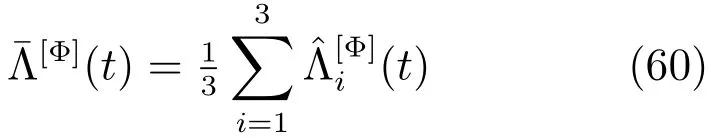

图1给出了应用部分3参数融合辨识算法获得的未知模型参数融合辨识结果.由图可知随着时间的增长,辨识结果收敛于真值.
图2和图3分别给出了未知模型参数a11和a12的局部估计误差方差、加权平均估计误差方差和分布式融合估计误差方差的比较结果.由图可知分布式加权融合辨识误差方差小于各局部辨识误差方差和加权平均辨识误差方差.图中Si,i=1,2,3表示第i个传感器的局部辨识的误差方差,DWF表示分布式加权融合辨识的误差方差,WAEV表示加权平均融合辨识的误差方差.
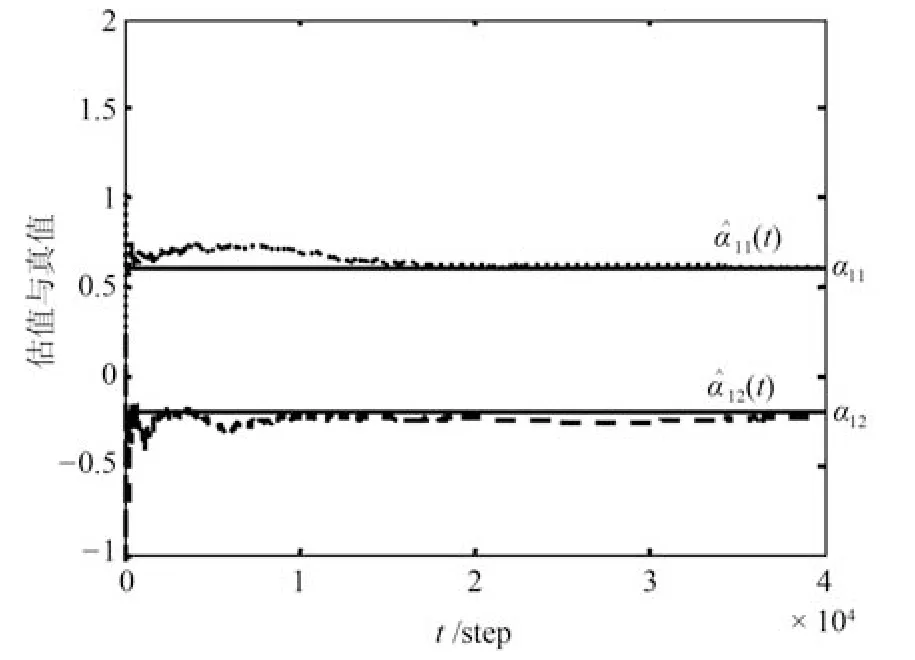
图1 Φ中未知参数估计Fig.1 Identif ication of parameters of Φ
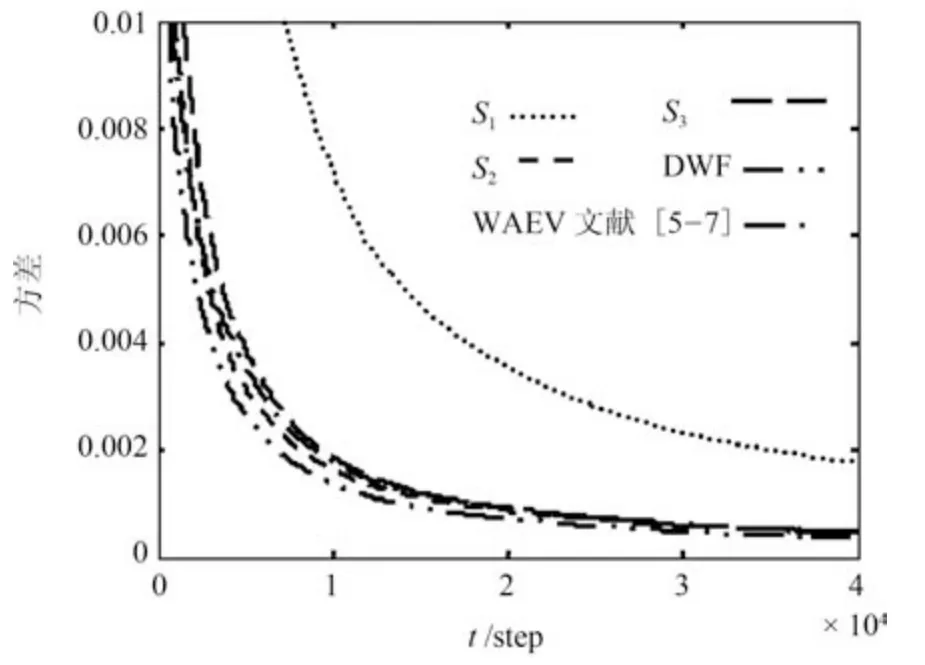
图2 a11估计误差方差Fig.2 Estimation error variance of a11
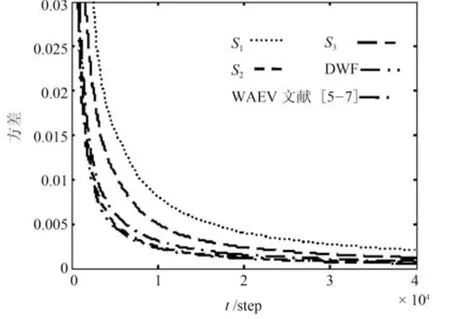
图3 a12估计误差方差Fig.3 Estimation error variance of a12
图4和图5给出了应用部分4中辨识算法分别对不同传感器的随机变量{µi(t)},i=1,2,3的数学期望和方差进行辨识的结果.曲线表示辨识结果,直线表示相应的真值.由图可知随着时间的增长,辨识结果收敛于真值.图6和图7 给出了自校正融合状态滤波器,可见自校正融合估计具有有效性.
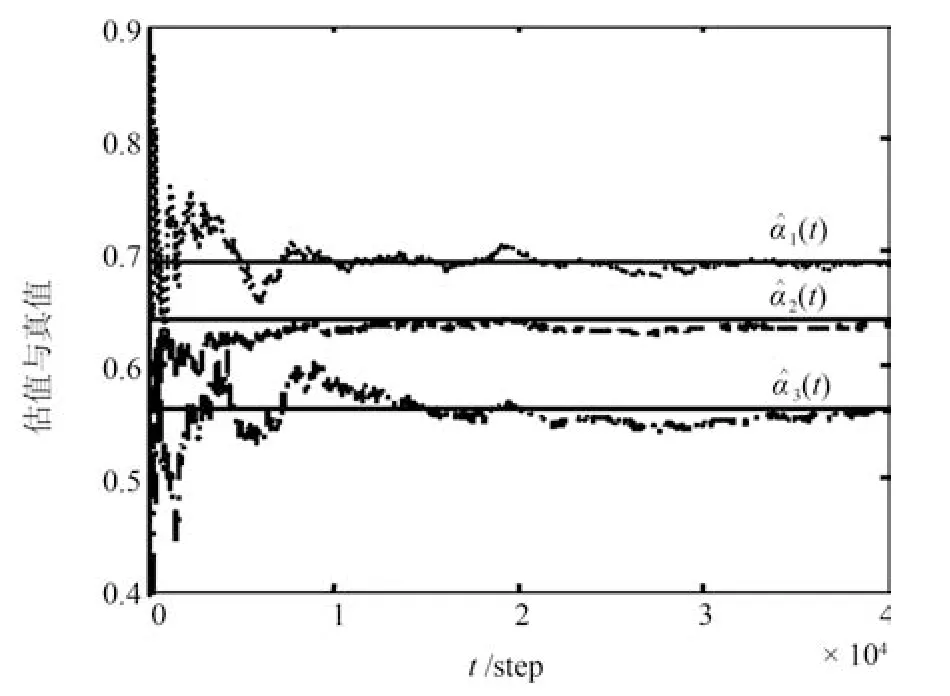
图4 µi(t)的数学期望辨识Fig.4 Identif ication of Mathematical expectation of µi(t)
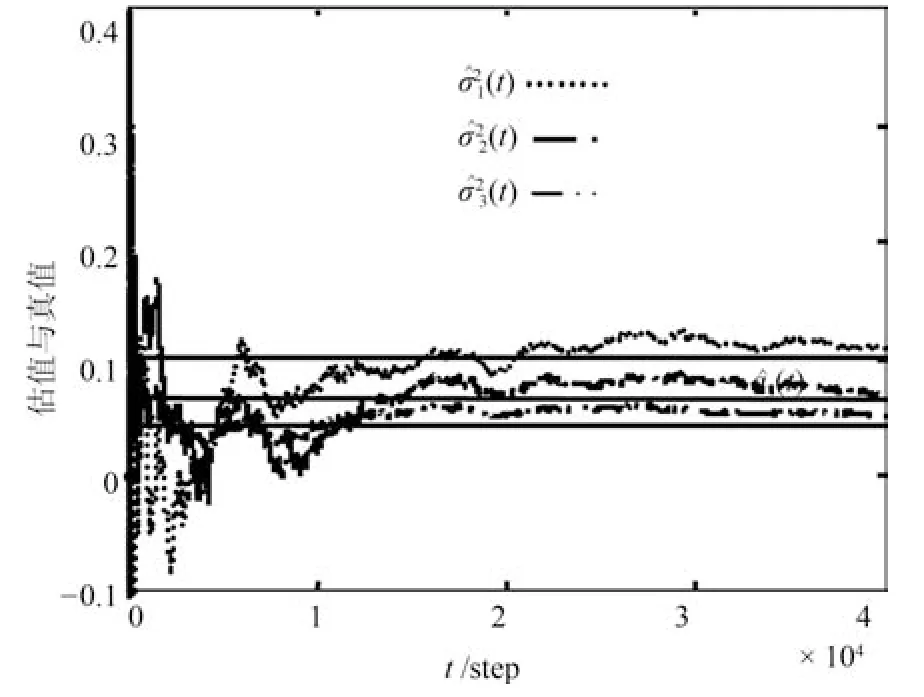
图5 µi(t)的方差辨识Fig.5 Identif ication of variance of µi(t)
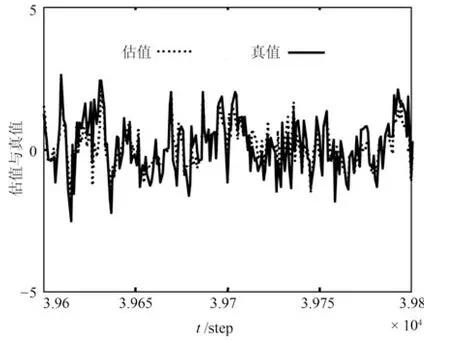
图6 自校正状态分量1融合滤波器Fig.6 The first state component of self-tuning fusion filter
图8和图9给出了局部和融合的最优与自校正状态估计误差方差图.由图可见,各局部自校正误差方差收敛于局部最优误差方差,自校正融合误差方差收敛于最优融合误差方差,即自校正滤波器具有渐近最优性.而且自校正融合滤波器比各局部自校正滤波器具有更高精度.图中Si,i=1,2,3表示第i个传感器的局部自校正估计误差方差,SF表示自校正融合估计误差方差,直线表示相应的最优方差.
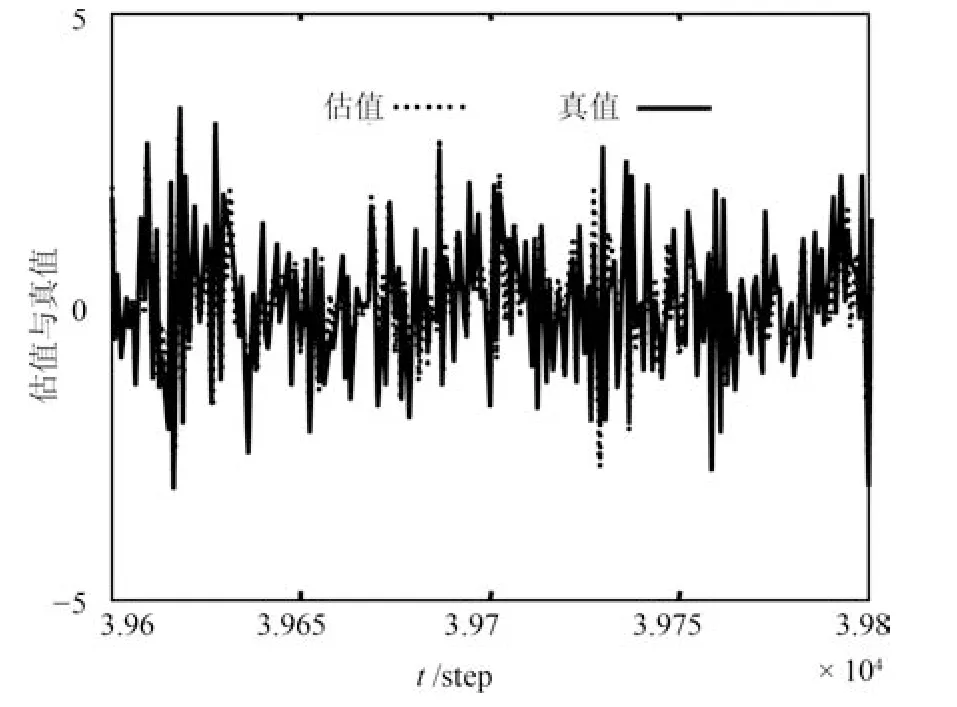
图7 自校正状态分量2融合滤波器Fig.7 The second state component of self-tuning fusion filter
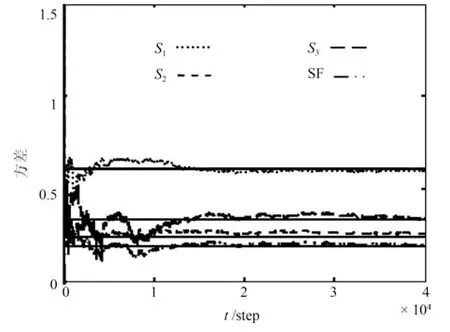
图8 局部、融合最优与自校正状态分量1的滤波误差方差Fig.8 Variance of the first state component of local,fusion optimal and self-tuning flters
目前参考文献[5−7,24]中的自校正滤波算法大都没有考虑传感器的衰减观测现象.图10给出了传感器存在衰减观测而没有给予考虑的自校正融合滤波器与本文考虑衰减观测的自校正融合滤波器在30次蒙特卡洛实验下均方误差迹的比较.可见,在传感器存在衰减观测时,本文考虑衰减观测的自校正融合滤波器具有更高的精度.
7 结论
对带未知模型参数和衰减观测率的多传感器随机系统,应用RELS算法和相关函数分别对未知模型参数、描述衰减观测现象的随机变量的数学期望和方差进行在线实时辨识,提出了线性无偏最小方差矩阵加权融合模型参数辨识器.与已有文献的加权平均融合模型参数辨识算法相比,本文所提出的线性无偏最小方差矩阵加权融合参数辨识算法具有更高的估计精度.将实时辨识的模型参数、数学期望和方差代入到最优局部和融合状态估计算法中获得了相应的自校正状态滤波算法.利用DESA方法证明了自校正状态滤波器收敛于最优状态滤波器.与现有文献的带未知模型参数的自校正估计算法相比,本文还考虑了传感器的衰减观测现象,并给出了采用相关函数辨识衰减观测的数学期望和方差的算法.
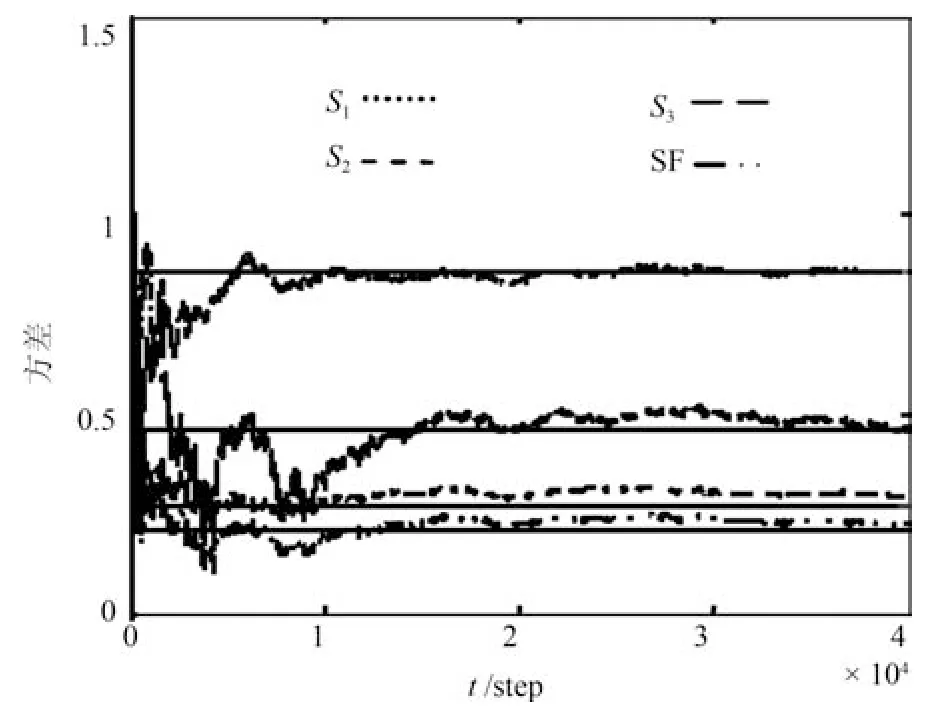
图9 局部、融合最优与自校正状态分量2的滤波误差方差Fig.9 Variance of the second state component of local,fusion optimal and self-tuning filters
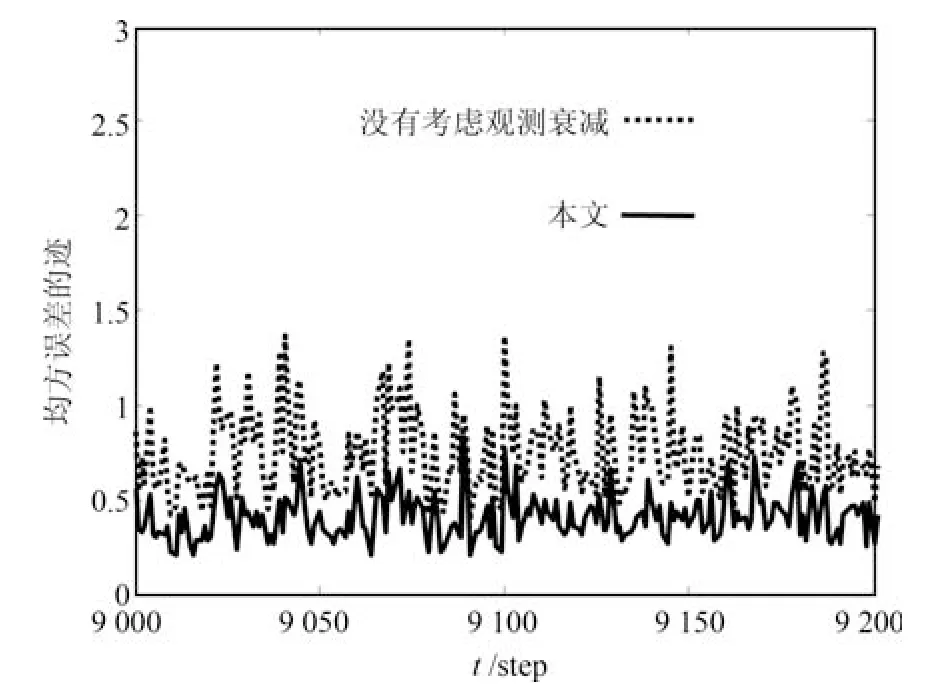
图10 考虑衰减观测与没有考虑衰减观测自校正融合滤波器的均方误差的迹Fig.10 Trace of mean square error of the self-tuning fusion flters with/without considering fading measurements
