自耦PID 控制器

曾喆昭 刘文珏

半个多世纪以来,经典控制理论(控制论)与现代控制理论(模型论)独立发展,形成了各自的方法论体系.在实际控制工程中,控制目标与被控对象实际行为之间的误差是容易获取的,也是能够适当加以处理的,因而“基于误差来消除误差”的控制策略的原形:比例–积分–微分(Proportional-integral-dif ferential,PID)控制器在实际工业控制领域获得了广泛应用[1−6].对于实际控制工程问题,通常难以给出其内部机理的精确描述,因而基于数学模型的现代控制理论给出的控制策略,在实际控制工程领域难以获得有效应用,这就是控制工程实践与控制理论之间延续了半个多世纪而难以获得很好解决的脱节现象[7−9].经典控制理论的精髓就是根据被控对象的实际值与期望值(控制目标)之间的偏差来形成控制策略,只要合理选择PID控制器的增益参数使闭环系统稳定就能够实现控制目标,这正是经典PID控制方法获得广泛应用的根本原因.然而,科学技术的发展对控制器的控制精度、响应速度和鲁棒稳定性提出了更高的要求,导致传统PID控制器的缺点也逐渐展现出来[9−10]:尽管传统PID控制系统能够保证闭环系统稳定,然而,闭环控制系统的动态品质对PID增益参数的变化敏感.正是这个缺点导致了快速性和超调之间不可调和的矛盾[10],因此,当系统运行工况发生变化时,控制器增益也需要随之变化,因而各种改进型PID控制方法应运而生.在对PID参数进行在线整定的过程中,由于PID增益参数的整定值只是局部优化值,而不是全局性的最优值,因而在线整定PID增益参数的这种控制方法无法从根本上解决动态品质和稳态精度的矛盾[11].因此,PID控制器增益参数的调节与优化一直是控制理论与控制工程领域广泛关注的问题.二十余年来,PID控制器在理论研究方面取得了长足发展,经典PID控制器与其他控制理论方法相结合形成了一些新型的PID控制器,例如:基于知识推理的专家PID控制[12]、基于神经网络的PID控制[11,13−17]、模糊PID控制[18]、预测PID控制[19]等.此外,一些现代优化方法也被应用于PID控制器的设计,如采用遗传算法[20]、粒子群算法[21]以及其他优化方法[22−23]求取满足设计要求的PID控制器参数.前面这些方法在PID优化控制方面都获得了不同程度的控制效果,具有良好的跟踪性能和一定的抗干扰性能,然而都存在计算量大的问题,在实时控制方面存在不同程度的局限性.为了减小PID增益参数在线优化的计算量,曾喆昭提出了非线性PID自学习控制方法[24−25],该方法不仅有效提高了非线性系统的自适应控制能力,而且具有响应速度快、控制精度高、鲁棒稳定性好等特点,然而,抗扰动能力仍然欠佳.由于传统PID控制原理是将误差的过去(I)、现在(P)和将来(变化趋势D)进行加权求和来形成控制信号,尽管只要合理选取PID三个增益参数就能使闭环控制系统局部稳定,然而,误差以及误差的积分和微分是三个完全不同属性的物理量,曾喆昭学者认为:将三个不同属性的物理量独立加权求和来形成PID控制律模型是不合理的:

1)违背了算术运算的基本规则:不同属性的物理环节是不能独立加权求和的,否则难以从物理意义上来准确理解传统PID控制律的数学模型;

2)传统PID控制律的数学模型不异于强行将比例、积分和微分等三个不同属性的物理环节割离开来并独立对待,由此导致了比例、积分和微分三个环节在控制过程中相互独立、各自为阵,因而缺乏协同控制的科学思想;

3)正因为传统PID控制律模型的不合理性,导致PID的增益整定问题成为了控制科学与控制工程领域的世纪难题.

曾喆昭学者发现:尽管误差的比例、积分和微分是三个不同属性的物理环节,然而这三个环节都与误差有关,三者之间一定存在某种内在的必然关系,因此不应该将比例、积分和微分等三个不同属性的环节割离开来并独立对待,而应该将三个不同属性的环节作为一个不可分割且有机统一的整体来对待.近十年来,曾喆昭学者在吸取PID控制、滑模控制(Sliding mode control,SMC)以及自抗扰控制(Auto disturbance rejection controller,ADRC)三大主流控制器优点的同时,主要围绕其各自存在的局限性开展了相关改进性的研究工作,特别是受跟踪微分器(Tracking dif ferentiator,TD)模型思想的启发,先后提出了SC-PID控制方法和ASF模型.本文的理论研究结果与数值仿真实验都验证了SC-PID控制思想的正确性.

1 问题描述

考虑到PID包括PI和PD等三种控制器类型,因此本文要研究的SC-PID也包括相应的三种类型,即SC-PI、SC-PID和SC-PD.考虑到PI控制器的广泛应用,下面先研究SC-PI 控制方法,然后再研究SC-PID和SC-PD控制方法.

1.1 一阶非仿射非线性不确定系统

考虑一阶非仿射非线性不确定系统:

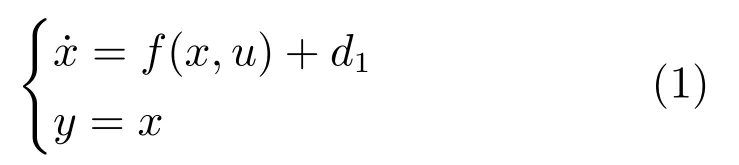
其中,x∈R是可测量状态,u∈R是控制输入,y∈R是系统输出,f(x,u)是未知不确定函数,d1是未知外部有界扰动.

由于系统(1)是一类一阶非仿射非线性不确定系统,因此本文将系统未知不确定动态和外部扰动定义为总和扰动,即

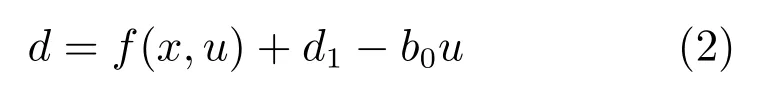
其中,b0=0是控制增益的估计值(不要求精确估计).

因此,系统(1)改写为

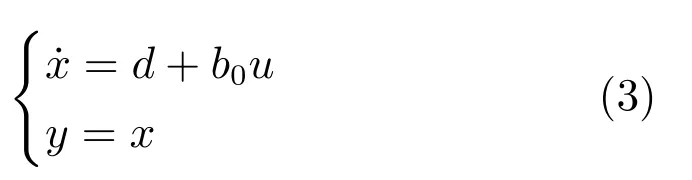
显然,系统(3)是一类一阶线性不确定仿射系统,而且与系统(1)是等价的.

1.2 二阶非仿射非线性不确定系统

考虑二阶非仿射非线性系统为:

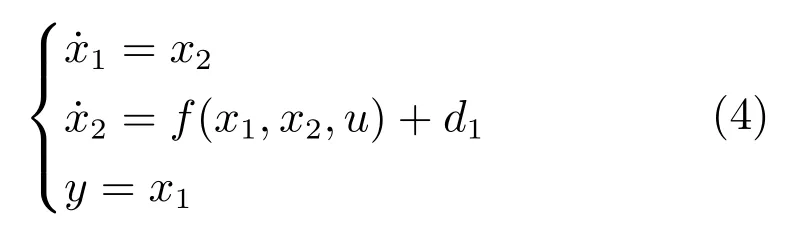
其中,x1,x2∈R是可测量的两个状态,u∈R是控制输入,y∈R是系统输出,f(x1,x2,u)是未知不确定函数,d1是未知外部有界扰动.

由于系统(4)是一类二阶非仿射非线性不确定系统,因此本文将系统未知不确定动态和外部扰动定义为总和扰动,即

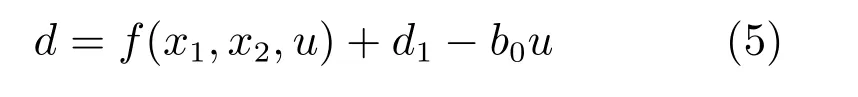
其中,b0=0是控制增益的估计值(不要求精确估计).

因此,系统(4)改写为

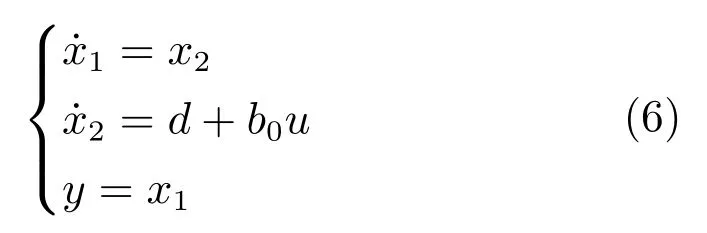
显然,系统(6)是一类二阶线性不确定仿射系统,而且与系统(4)是等价的.

本节的主要思想是:将一类非仿射非线性不确定系统转换为一类线性不确定仿射系统.其主要特色是:淡化了线性与非线性、时变与时不变性、确定与不确定、仿射与非仿射等系统分类的概念或界定,将一类复杂非线性系统的控制问题转化为一类线性不确定仿射系统的控制问题.尽管系统(1)和系统(4)没有显含时变参数,但是可以将系统的时变性归类于系统内部的不确定性.

2 SC-PID控制器研究

针对一阶和二阶线性不确定仿射系统的控制问题,分别进行相应的SC-PID控制器设计.

2.1 SC-PI控制器设计

设被控系统的期望轨迹为r,针对一阶非仿射非线性不确定系统(1)或其等价的线性不确定仿射系统(3)的控制问题,定义跟踪控制误差为:

定义误差的积分:

结合系统(3)可得:

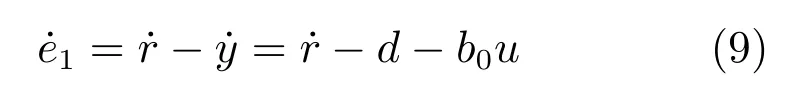
根据式(7)∼(9)可得受控误差系统:

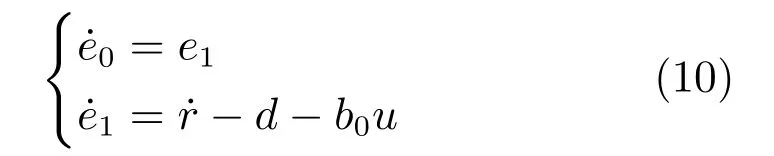
由受控误差系统(10)定义SC-PI 控制器模型为:

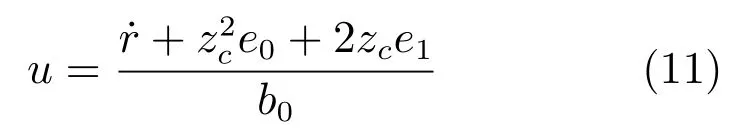
其中,zc >0是SC-PI控制器的速度因子.

基于SC-PI 的闭环控制系统如图1所示.

与传统PI 控制器相比,SC-PI控制器(11)的主要创新点在于只有一个速度因子zc;其主要特色是:通过zc将比例和积分两个不同属性的物理环节紧密耦合在一起形成协同控制信号,因此,SC-PI的增益整定规则为:

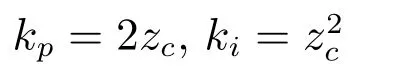
传统PI控制器将kp和ki两者分离开来并独立对待,是否存在合理性问题,作者不予过多评价.然而,PI控制器的增益整定问题一直是个世纪难题.

2.2 SC-PID控制器设计

被控系统的期望轨迹为r,针对二阶非仿射非线性不确定系统(4)或与其等价的线性不确定仿射系统(6)的控制问题,定义跟踪控制误差为:

定义误差的积分:

结合系统(6)可得:

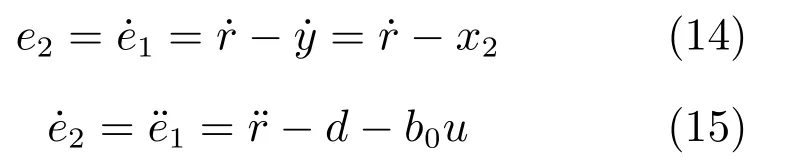
根据式(13)∼(15)可得受控误差系统:

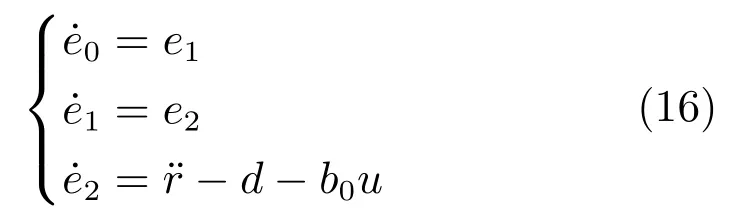
由受控误差系统(16)定义SC-PID控制器模型为:

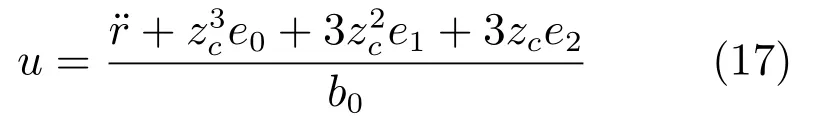
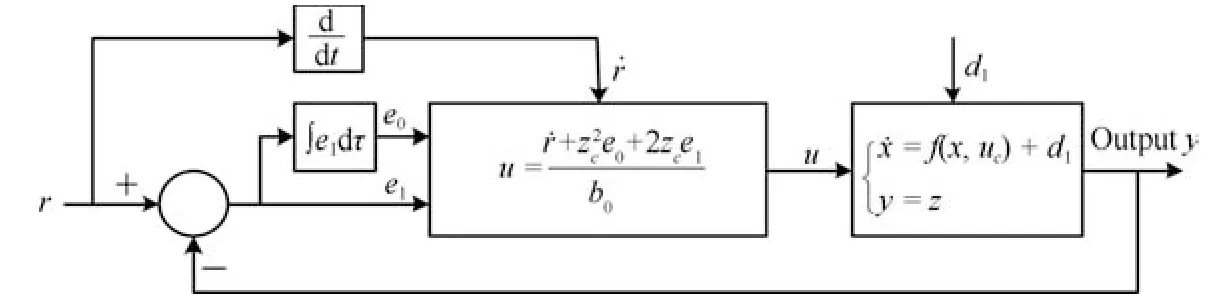
图1 基于SC-PI 的闭环控制系统模型Fig.1 Closed loop control system based on SC-PI

其中,zc>0是SC-PID控制器的速度因子.

基于SC-PID的闭环控制系统如图2所示.

与传统PID控制器相比,SC-PID控制器(17)的主要创新点在于只有一个速度因子zc;其主要特色是通过zc将比例、积分和微分等三个不同属性的物理环节紧密耦合在一起来形成控制信号,因此,SC-PID的增益整定规则为:

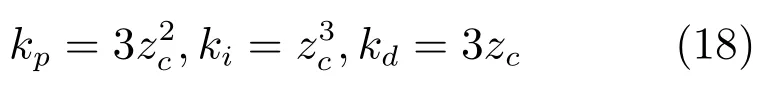
就控制论而言,PID及其各种改进型PID控制器都是多参数的控制器.从目前已有的研究成果来看,这些控制器的各参数之间是完全独立的,而且与被控对象有关:对于不同的被控对象,PID控制器的增益千差万别;即便是同一个对象,当系统模型参数发生变化或工况状态发生变化时,必须重新整定PID的三个增益参数.显然,尽管PID的控制律不依赖于被控对象,然而,PID的三个增益参数却与被控对象相关,因此,传统PID的增益整定方法背离了控制论的精髓,从而导致了增益整定的世纪难题.从理论上来说,独立的多参数控制器确实增加了可行域的选择范围,然而从实际控制工程而言,却显著增加了各参数的整定难度.

作者发现:尽管比例、积分和微分是三个不同属性的物理环节,然而却都与误差有关,因此,三个不同属性的环节之间一定存在内在的必然联系,而且一定是一个不可分割且有机统一的整体.SC-PID控制器中的速度因子zc >0正是将比例–积分–微分等三个不同属性环节紧密耦合在一起的内在关键因子.

2.3 SC-PD控制器设计

如果不考虑积分环节,根据式(14)和(15)可得受控误差系统为:

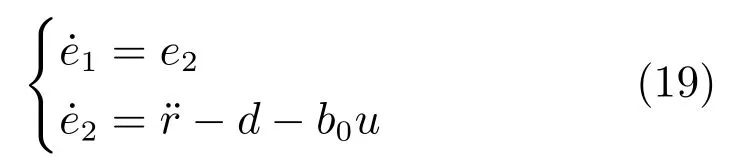
由受控误差系统(19)定义SC-PD控制器模型为:

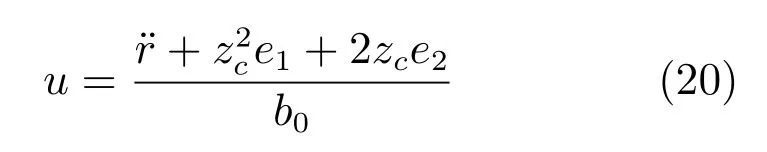
其中,zc >0是SC-PD控制器的速度因子.

基于SC-PD的闭环控制系统如图3所示.

与传统PD控制器相比,SC-PD控制器(20)的主要创新点在于只有一个速度因子zc;其主要特色是通过zc将比例和微分两个不同属性的物理环节紧密耦合在一起来形成控制信号,因此,SC-PD的增益整定规则为:

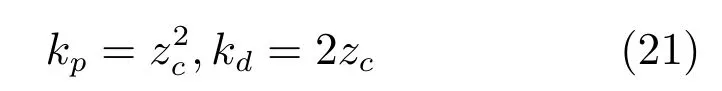
3 控制系统分析与自适应速度因子

本文设计了SC-PI、SC-PID和SC-PD等三类自耦PID控制器,由这三类控制器分别构成的闭环控制系统是否稳定正是本文要重点研究的主要内容之一.

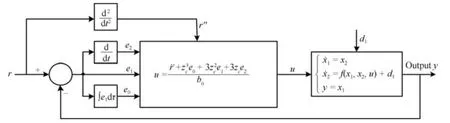
图2 基于SC-PID的闭环控制系统模型Fig.2 Closed loop control system based on SC-PID

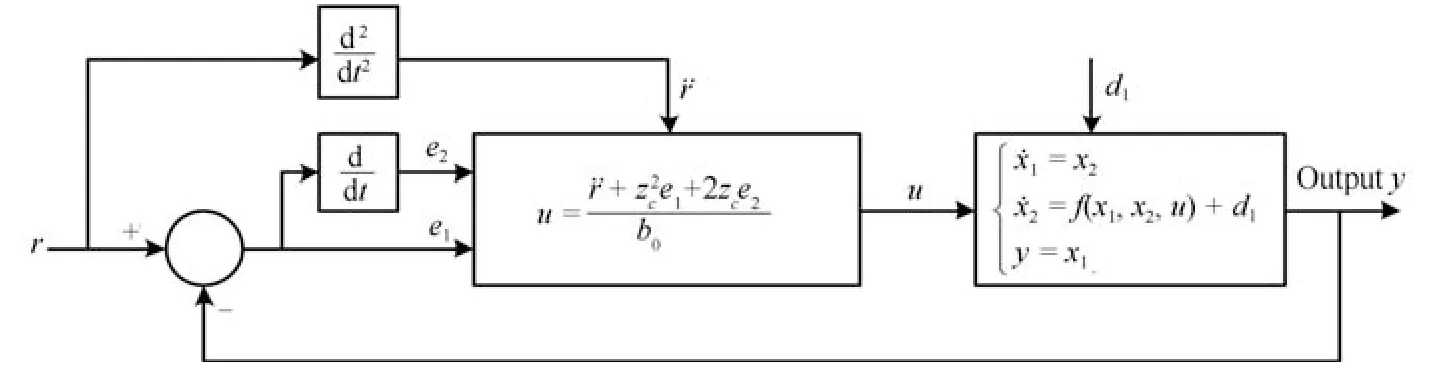
图3 基于SC-PD的闭环控制系统模型Fig.3 Closed loop control system based on SC-PD

3.1 控制系统分析

定理1.假设式(2)定义的总和扰动有界:|d|<∞,则当且仅当速度因子zc>0时,由式(11)定义的SC-PI 控制器组成的闭环控制系统是大范围稳定的,而且SC-PI 控制系统具有良好的抗总和扰动鲁棒性.

证明.

1)稳定性分析

将式(11)定义的SC-PI 控制器代入式(10)所示的受控误差系统,可得闭环控制系统:

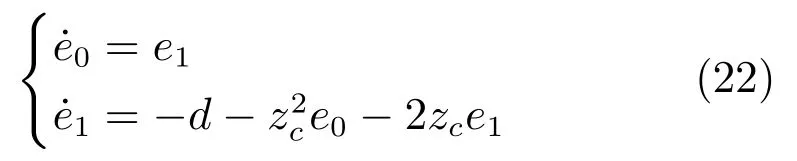
显然,闭环控制系统(22)是一个在总和扰动d反相激励下的误差动态系统.考虑到初始状态:=0,对系统(22)取单边拉普拉斯变换,并整理得:

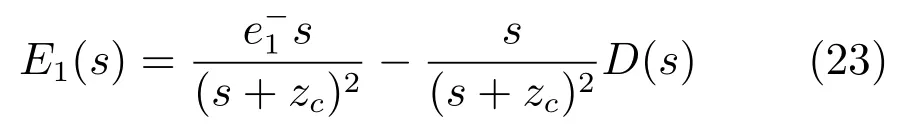
其中,系统(23)的第一项是零输入响应,第二项是零状态响应.

由系统(23)可得闭环控制系统的传输函数为:

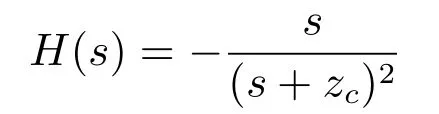
相应的单位冲激响应为:

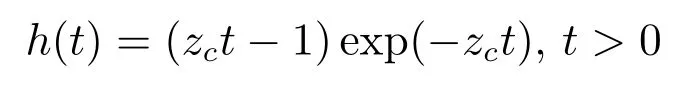
当zc >0时,则有:limt→∞h(t)=0.显然,参数zc越大,h(t)→0的速度则越快,因此称zc为速度因子,下同.当zc >0时,由于闭环控制系统的传输函数唯一的双重极点sp=−zc <0在S左半平面,因此,闭环控制系统(22)或(23)是大范围稳定的.

2)抗扰动鲁棒性分析

闭环控制系统(23)的时域解为:

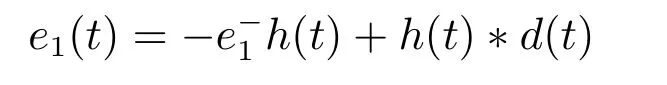
当zc >0时,由于limt→∞h(t)=0,因此,只要|d|<∞,则必有下式成立:

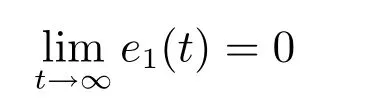
理论分析表明,在式(11)定义的SC-PI 控制器作用下,被控系统(1)或(3)的跟踪控制误差e1=r−y可以从任意不为零的初始状态e−1=0向稳定的平衡点零点趋近,理论上可以实现精确控制.当zc>0时,由于e1(t)→0只与|d|<∞有关,而与总和扰动d的具体模型无关,因此,SC-PI控制器具有良好的抗总和扰动鲁棒性.

上述复频域分析和时域分析表明,当速度因子zc >0时,不仅由SC-PI 控制器组成的闭环控制系统是大范围稳定的,而且只要|d|<∞,跟踪控制误差可以从任意不为零的初始状态向稳定的平衡点零点趋近,因而具有良好的抗总和扰动鲁棒性.

定理2.假设式(5)定义的总和扰动有界:|d|<∞,则当且仅当速度因子zc >0时,由式(17)定义的SC-PID控制器组成的闭环控制系统是大范围稳定的,而且SC-PID控制器具有良好的抗总和扰动鲁棒性.

证明.

1)稳定性分析

将式(17)定义的SC-PID控制器代入式(16)所示的受控误差系统,可得闭环控制系统:

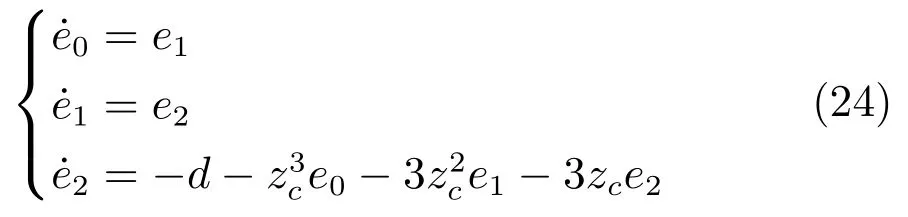
显然,闭环控制系统(24)是一个在总和扰动d反相激励下的误差动态系统.考虑到初始状态:

其中,系统(25)的第一项是零输入响应,第二项是零状态响应.

且闭环控制系统的传输函数为:

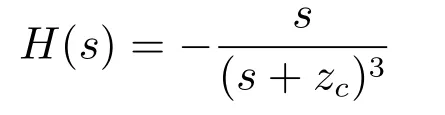
其单位冲激响应为:

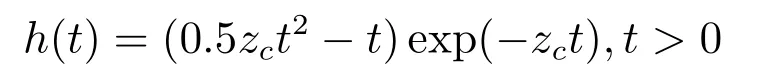
且

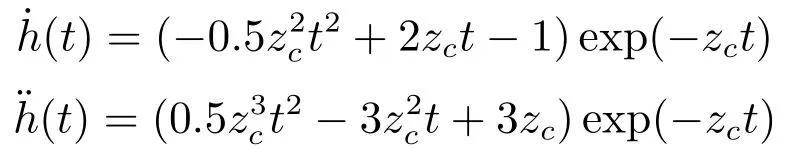
由于zc >0时,闭环控制系统传输函数唯一的三重极点sp=−zc <0在S左半平面,因此,闭环控制系统(24)或(25)是全局渐近稳定的.

2)抗扰动鲁棒性分析

闭环控制系统(24)或(25)的时域解为:

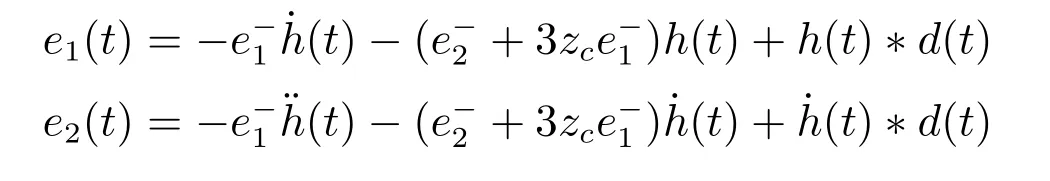
当zc >0时,由于:

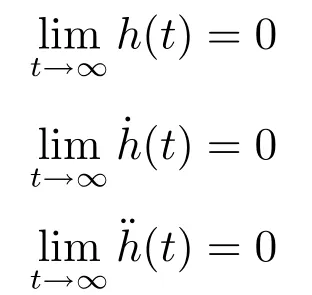
因此,只要|d|<∞,则必有下式成立:

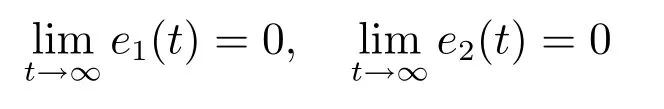
理论分析表明,在式(17)定义的SC-PID控制器作用下,被控系统(4)或(6)的跟踪控制误差e1=r−y及其微分可以从任意不为零的初始状态向稳定的平衡点原点(0,0)趋近,理论上可以实现精确控制.当zc >0时,由于(e1,e2)→(0,0)只与|d|<∞有关,而与总和扰动d的具体模型无关,因此,SC-PID控制器具有良好的抗总和扰动鲁棒性.

上述复频域分析和时域分析表明,当速度因子zc >0时,不仅由SC-PID控制器组成的闭环控制系统是大范围稳定的,而且只要|d|<∞,跟踪误差及其微分可以从任意不为零的初始状态向稳定的平衡点原点(0,0)趋近,因而具有良好的抗总和扰动鲁棒性.

定理3.假设式(5)定义的总和扰动有界:|d|<∞,则当且仅当速度因子zc>0时,由式(20)定义的SC-PD控制器组成的闭环控制系统是大范围稳定的,且SC-PD控制系统具有良好的抗总和扰动鲁棒性.

证明.

1)稳定性分析

将式(20)定义的SC-PD控制器代入式(19)所示的受控误差系统,可得闭环控制系统:

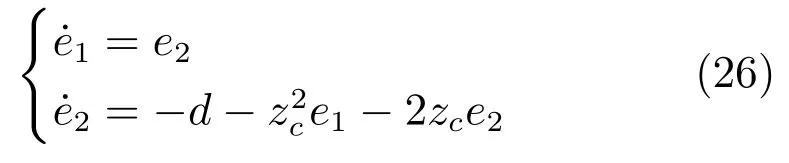
显然,闭环控制系统(26)是一个在总和扰动d反相激励下的误差动态系统.考虑到初始状态:对系统(26)取单边拉普拉斯变换,并整理得:

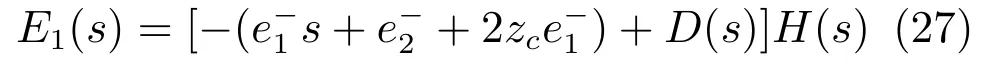
其中,误差系统(27)的第一项是零输入响应,第二项是零状态响应.

且闭环控制系统的传输函数为:

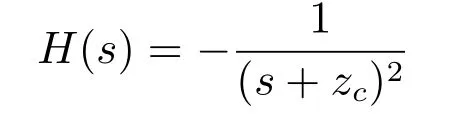
其单位冲激响应为:

且

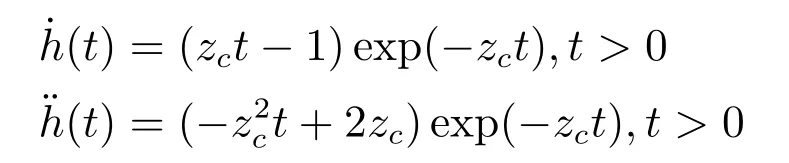
由于zc >0时,闭环控制系统传输函数唯一的二重极点sp=−zc <0在S左半平面,因此,闭环控制系统(26)或(27)是大范围稳定的.

2)抗扰动鲁棒性分析

闭环控制系统(26)或(27)的时域解为:

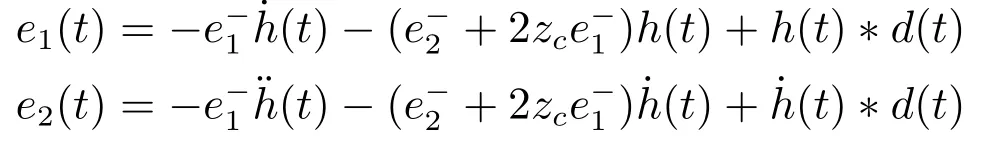
当zc >0时,由于:

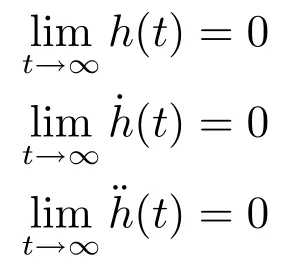
因此,只要|d|<∞,则必有下式成立:

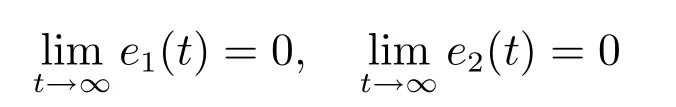
理论分析表明,在式(20)定义的SC-PD控制器作用下,被控系统(4)或(6)的跟踪控制误差e1=r−y及其微分可以从任意不为零的初始状态向稳定的平衡点原点(0,0)趋近,理论上可以实现精确控制.当zc >0时,由于(e1,e2)→(0,0)只与|d|<∞有关,而与总和扰动d的具体模型无关,因此,SC-PID控制系统具有良好的抗总和扰动鲁棒性.

上述复频域分析和时域分析表明,当速度因子zc >0时,不仅由SC-PD控制器组成的闭环控制系统是大范围稳定的,而且只要|d|<∞,跟踪误差及其微分可以从任意不为零的初始状态向稳定的平衡点原点(0,0)趋近,具有良好的抗总和扰动鲁棒性.

3.2 自适应速度因子

尽管上述三个定理都表明了只要总和扰动有界:|d|<∞,且速度因子zc >0时,分别由SC-PI、SCPID和SC-PD组成的闭环控制系统都是大范围稳定的,而且SC-PI、SC-PID和SC-PD等控制系统分别具有良好的抗扰动鲁棒性,同时也表明了三类控制器的速度因子zc具有很大的整定裕度.为了提高控制系统的动态响应速度和抗扰动能力,要求zc越大越好.然而,如果zc太大,会使积分环节的增益权重很大,在动态响应初期,可能会因积分饱和而出现超调与振荡现象.因此,在保证响应速度快和抗扰动能力强的同时,为了避免因积分饱和问题出现超调与振荡现象,本文设计了一种自适应速度因子模型,即:

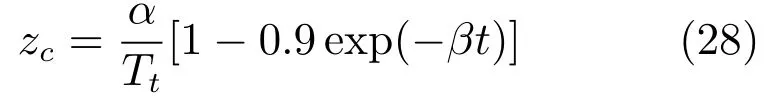
其中,0<α<100,β=1/Tt,Tt是由动态过渡到稳态的过渡过程时间.

为了便于实际应用,对于快系统而言,通常在10<α<100范围内任意取值;对于慢系统而言,通常在1≤α≤10范围内任意取值.α越大,则响应速度越快,抗扰动能力越强;否则反之.过渡过程时间Tt则由被控系统的时间尺度特性来确定:如果实际要求在1 s时间内实现稳态跟踪控制,则取Tt=1 s,依次类推.

3.3 SC-PID控制器合理性分析

由式(29)可知,由于过渡过程时间Tt的量纲是秒(s),因此,速度因子zc的量纲是:s−1.以被控对象(6)为例,假设x1和x2分别表示位移(米:m)和速度(米/秒:ms−1),因而其量纲分别为:m和ms−1.设期望输出为r,其量纲为:m,则有误差及其积分和微分分别为:

误差:e1=r−y,量纲:m;

积分:e0=e1dτ,量纲:ms;

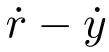
下面定性分析SC-PID中4个不同环节的物理属性:

显然,SC-PID控制器中各个不同环节通过速度因子转换后都成为相同的物理量纲:ms−2,即加速度量纲.假设系统增益系数b0的量纲为:kg−1,那么,控制信号u的量纲就是牛顿,因而控制信号u相当于力的地位,或者说,也称控制信号u为控制力.

上述仅是以位移运动系统为例进行类比定性分析,同样,也可以使用转动系统进行类比定性分析,在此不再一一列举.

总之,本文提出的SC-PID控制器模型,明确了各个不同属性的环节通过速度因子进行量纲转换后,都成为了力的属性单元,并通过加权求和来形成控制器的合力.本文指出传统PID控制律模型的不合理性,主要是针对三个独立增益而言的,并不是否定PID的历史地位及其历史功绩,而是作者近年来心存以下质疑:

1)比例增益、积分增益和微分增益究竟是什么属性？

2)三者之间是否存在必然的关系？

3)如何整定三个增益？

4)控制信号u是什么属性？

如何解决上述系列质疑问题,正是作者近年来一直思考的问题.在控制过程中,由于比例、积分和微分等三个不同环节之间互相影响,不明确解决上述问题,增益参数的整定永远都是一个难题.本文提出的SC-PID控制器正是为了解决这些质疑问题而问世的,它能够使没有任何控制理论基础或没有任何控制工程经验的人都可以对陌生的被控对象进行控制,因而也可称之为傻瓜型控制理论方法.

4 数值仿真实验与分析

为了验证本文提出的SC-PI、SC-PID和SCPD等三类控制方法的有效性,分别进行下列仿真实验.在仿真实验中,设期望轨迹分别为正弦信号和单位阶跃信号.考虑到SC-PID和SC-PD控制器都涉及到期望信号的微分信息,因此,针对期望轨迹为单位阶跃信号的情况,使用如下过渡过程:

4.1 考虑一阶非仿射非线性不确定系统[26−27]

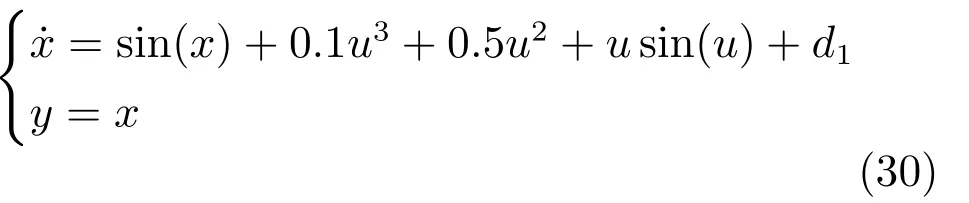
其中,系统未知动态为:

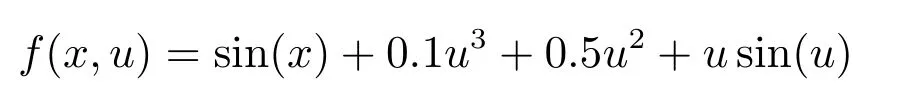
d1是幅值为±1的方波振荡外部扰动.设总和扰动为:d=f(x,u)+d1−b0u,给定初始状态为x(0)=0.5,设α=63,β=1,则SC-PI控制器的自适应速度为:

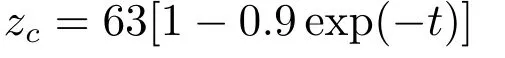
下列三个仿真实验都使用相同的控制器参数:

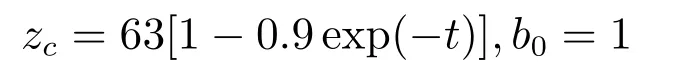
仿真实验1.SC-PI的正弦跟踪控制

当期望轨迹为正弦信号时,即r(t)=0.5 sin(2t),使用SC-PI控制器的仿真结果如图4所示.

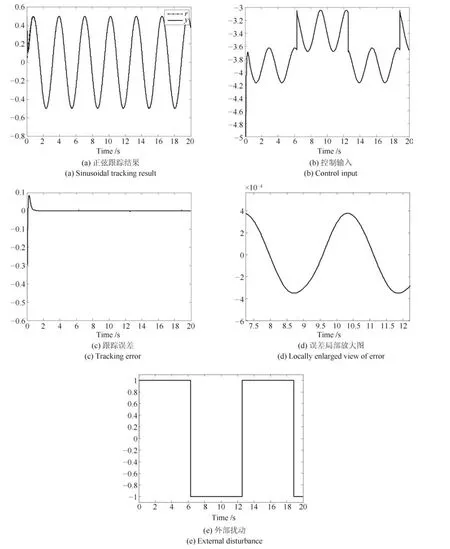
图4 SC-PI 的正弦跟踪控制结果Fig.4 Sinusoidal tracking control results of SC-PI

下列所有仿真实验中的外部扰动都与图4(e)完全相同,为了节省篇幅,不再一一列出.

仿真实验2.SC-PI的阶跃跟踪控制

当期望轨迹为单位阶跃信号时,使用SC-PI控制器的仿真结果如图5所示.由图4和图5可知,同一个SC-PI控制器可以实现正弦跟踪和阶跃跟踪两种不同工况状态的有效控制,不仅响应速度快、控制精度高、无超调、无波动、无抖振,而且具有很强的抗扰动能力,理论研究结果和仿真实验结果都表明了本文研究的SC-PI控制器是有效的.与文献[26]和[27]相比,本文的SC-PI控制方法因免除了扰动观测器,使得控制器结构更为简单,实时性更好.此外,文献[26]和[27]只做了正弦跟踪控制实验,没有进行阶跃跟踪控制实验.

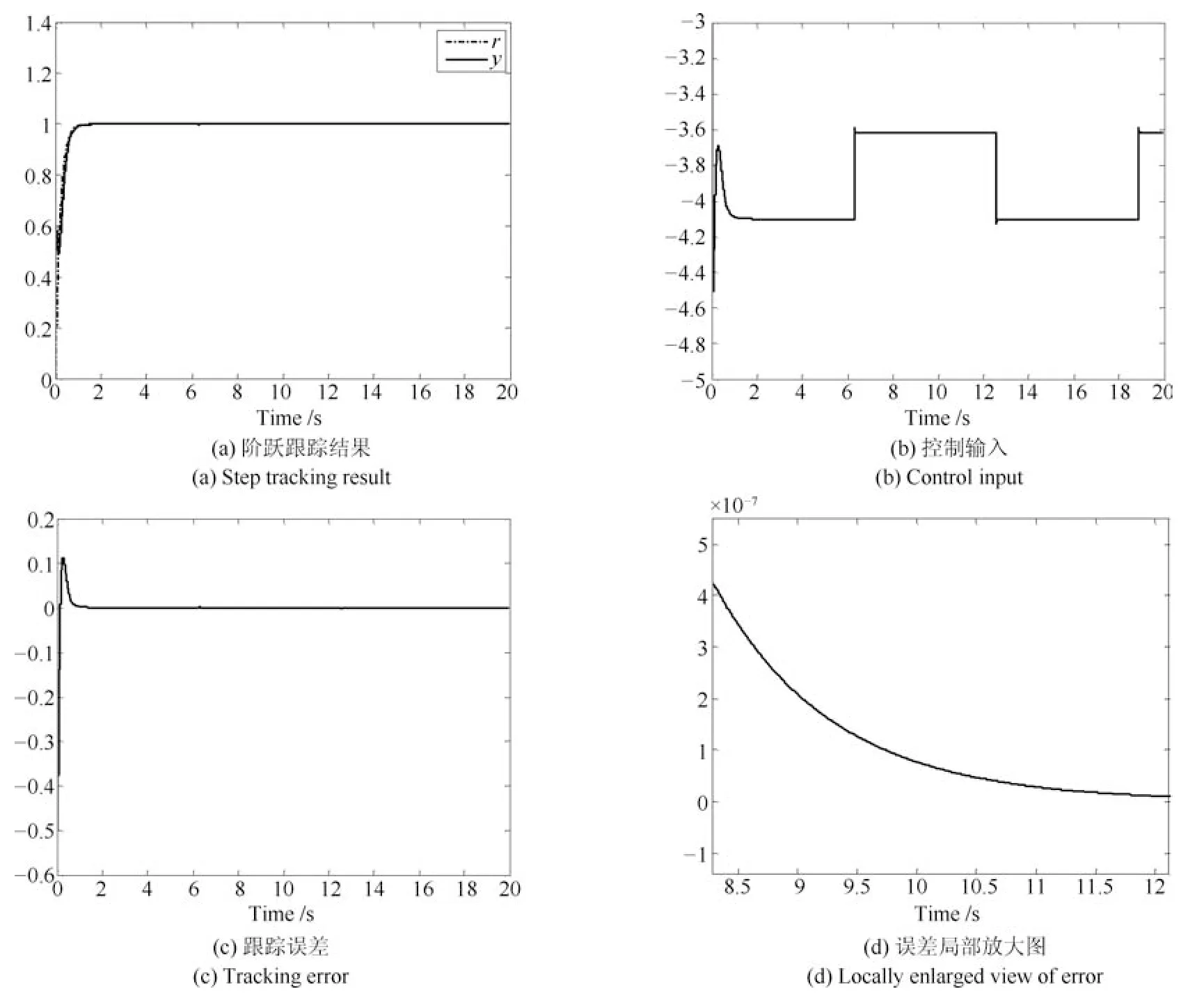
图5 SC-PI 的阶跃跟踪控制结果Fig.5 Step tracking control results of SC-PI

仿真实验3.时变系统的SC-PI阶跃跟踪控制

被控对象(30)中有三个模型参数1、0.1和0.5.假设这三个模型参数是时变的,且分别设为:

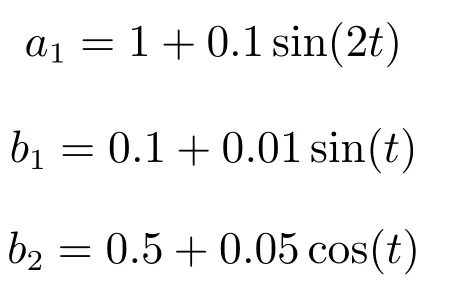
则一阶非仿射非线性不确定系统(30)变为非仿射非线性时变不确定系统(31)

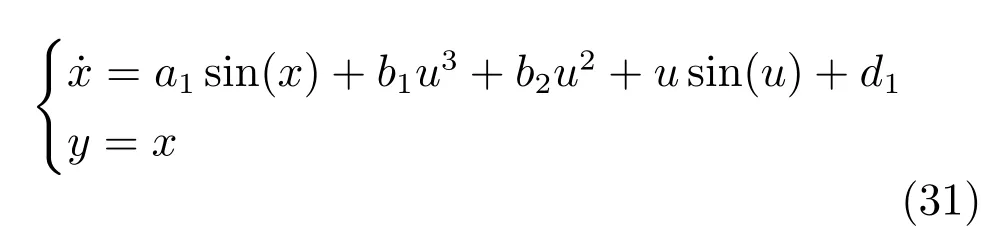
使用同一套SC-PI控制器对时变系统(31)进行阶跃跟踪控制实验,结果如图6所示.由图6可知,使用同一套SC-PI控制器对时变系统(31)进行阶跃跟踪控制实验,仍然获得了很好的控制效果,进一步表明了本文研究的SC-PI控制器对系统时变性和外部扰动具有很好的鲁棒性.

4.2 考虑二阶非仿射非线性不确定系统[26−27]

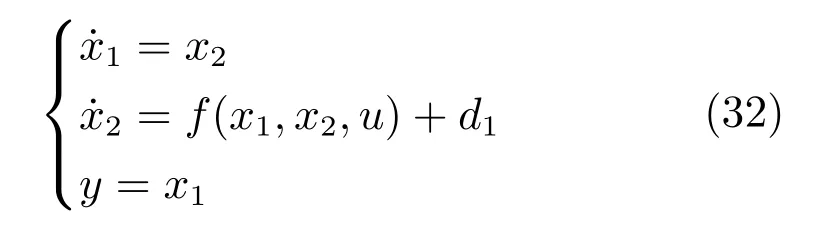
其中,d1为外部有界扰动.系统未知动态为:

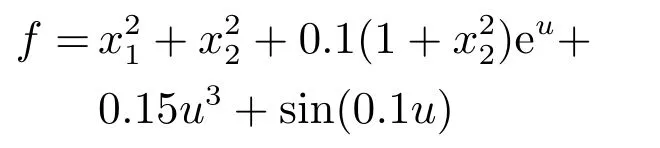
设总和扰动为:d=f(x1,x2,u)+d1−b0u.给定初始状态为x1(0)=x2(0)=0.5,设α=63,β=1,则SC-PID控制器的自适应速度为:

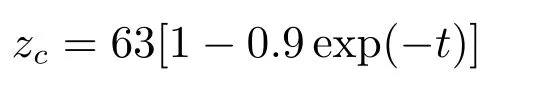
(与SC-PI的自适应速度完全相同).

下列三个仿真实验都使用同一套控制器参数:

仿真实验4.SC-PID的正弦跟踪控制

设期望的正弦轨迹与仿真实验1的完全相同,使用SC-PID控制器的仿真结果如图7 所示.

仿真实验5.SC-PID的阶跃跟踪控制

设期望的阶跃轨迹与仿真实验2的完全相同,使用SC-PID控制器的仿真结果如图8所示.由图7 和图8可知,同一套参数的SC-PID控制器可以实现正弦跟踪和阶跃跟踪两种不同工况状态的有效控制,不仅响应速度快、控制精度高、无超调、无波动、无抖振,而且具有很强的抗扰动能力,理论研究结果和仿真实验结果都表明了本文研究的SC-PID控制器是有效的.与文献[26]和[27]相比,本文的SC-PID控制方法因免除了扰动观测器,使得控制器结构更为简单,实时性显著提高.

仿真实验6.时变系统的SC-PID阶跃跟踪控制实验

被控对象(32)中未知动态函数:

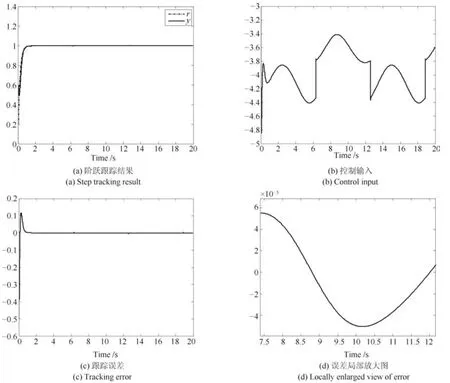
图6 时变系统的SC-PI 控制结果Fig.6 SC-PI control results for time-varying systems

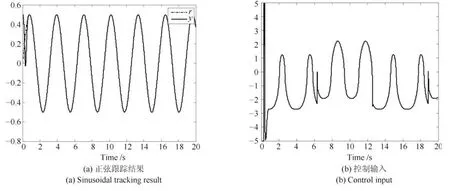
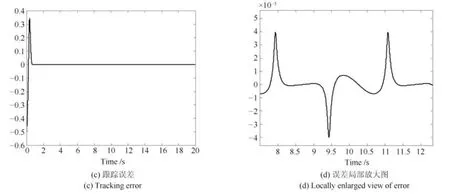
图7 SC-PID的正弦跟踪控制结果Fig.7 Sinusoidal tracking control results of SC-PID

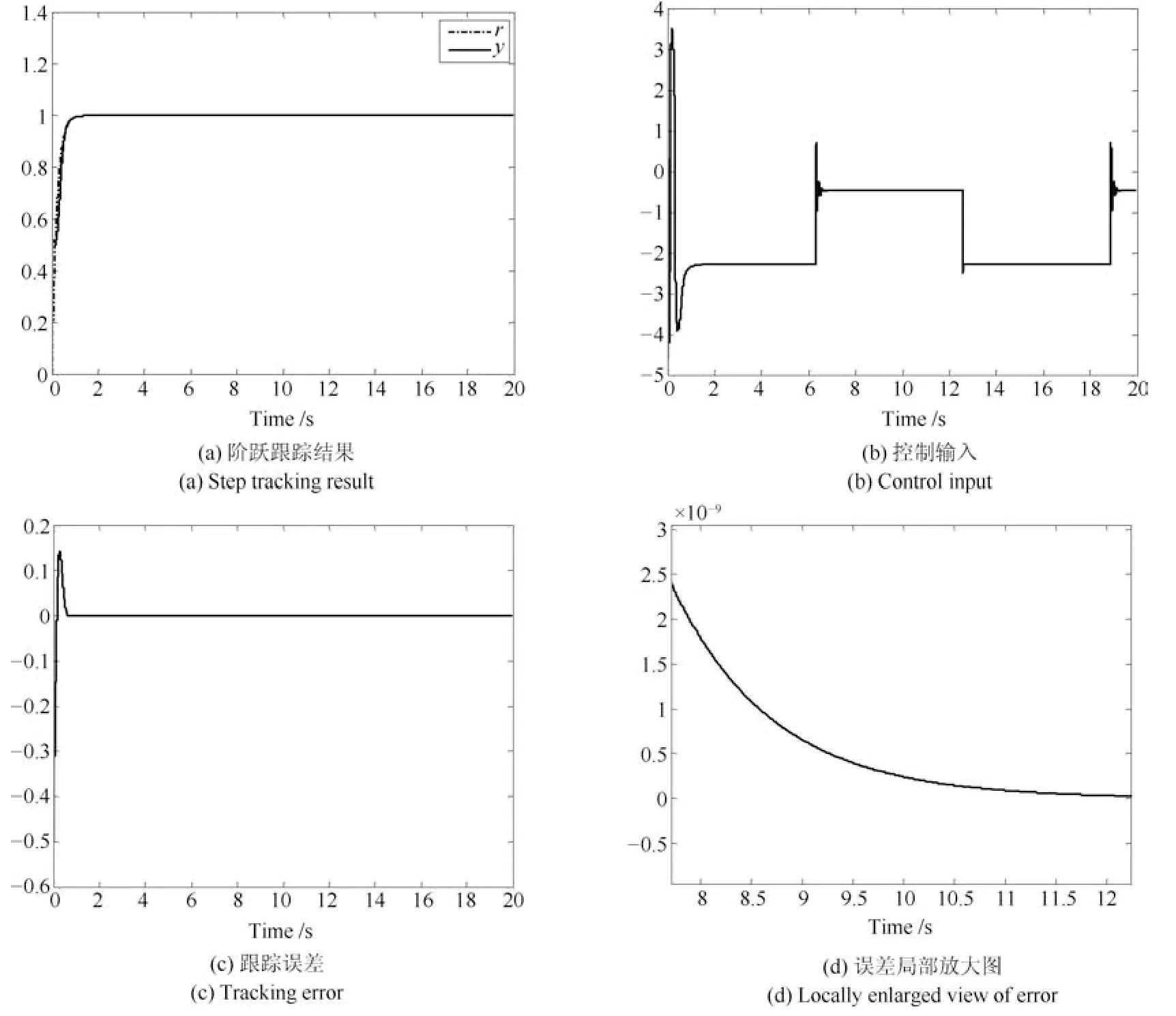
图8 SC-PID的阶跃跟踪控制结果Fig.8 Step tracking control results of SC-PID

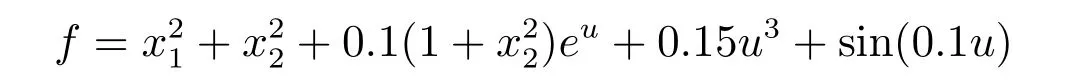
有5个系统模型参数1、1、0.1、0.15和1.假设这5个系统模型参数是时变的,且分别设为:

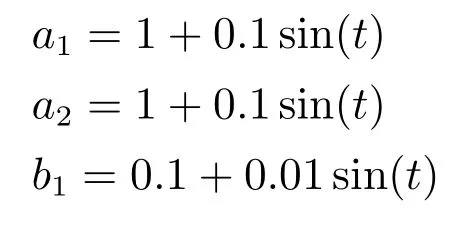
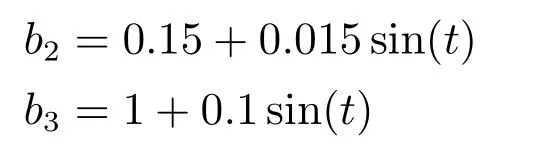
则二阶非仿射非线性不确定系统(32)的未知动态函数变为时变动态函数:

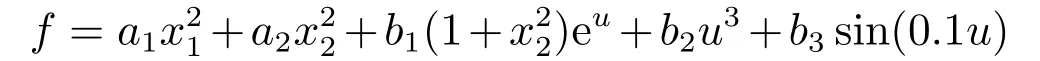
因而二阶非仿射非线性不确定系统(32)变为二阶非仿射非线性时变不确定系统.使用同一套SCPID控制器参数对时变系统(32)进行阶跃跟踪控制实验,结果如图9所示.由图9可知,使用同一套SC-PID控制器对时变系统(32)进行阶跃跟踪控制实验,仍然获得了很好的控制效果,进一步表明了本文研究的SC-PID控制器对系统时变性和外部扰动具有很好的鲁棒性.

上述6个仿真实验表明,SC-PI 控制器和SC-PID控制器使用完全相同的自适应速度因子zc=63[1−0.9 exp(−t)]分别控制两类不同模型、不同属性的被控对象,都获得了很好的控制效果.不仅如此,本文研究的控制方法,控制律和控制器增益都与被控对象无关,而PID控制器增益却完全与被控对象相关,对于不同的工况和不同的被控对象,PID及其各种改进型PID的增益千差万别.

为了验证SC-PD控制器的有效性,针对二阶非仿射非线性不确定系统(32)分别进行下列仿真实验.

考虑到SC-PD缺少积分环节,因此SC-PD的增益参数应该取大一点,即设α=83、β=1,则SCPD的自适应速度因子为:zc=83[1−0.9 exp(−t)].

期望的正弦轨迹和阶跃轨迹与上述实验的也完全相同.

仿真实验7.SC-PD的正弦跟踪控制

使用SC-PD的正弦跟踪控制结果如图10所示.

仿真实验8.SC-PD的阶跃跟踪控制

使用SC-PD控制器的阶跃跟踪控制结果如图11所示.

仿真实验9.时变系统的SC-PD阶跃跟踪控制

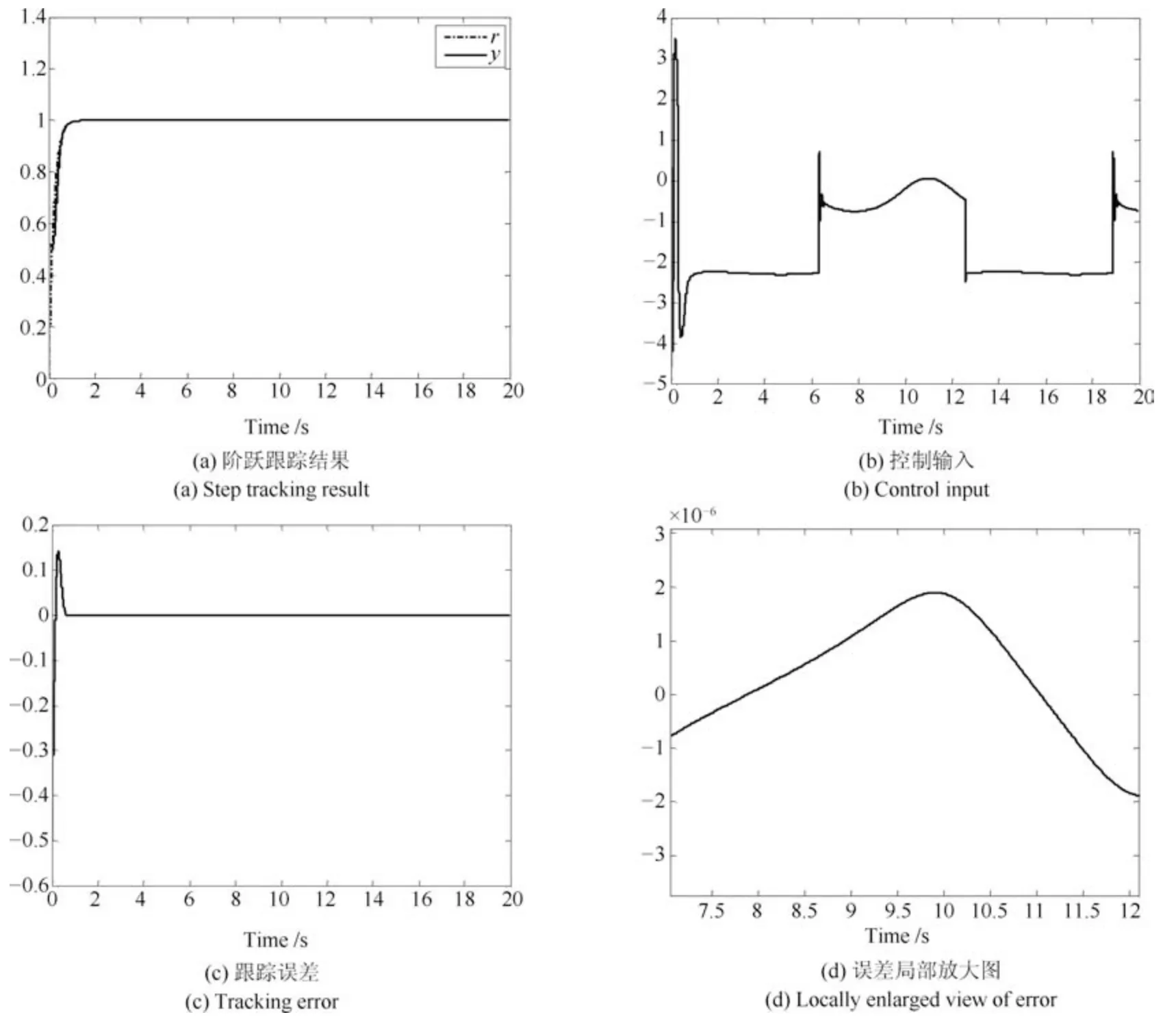
图9 时变系统的阶跃跟踪控制结果Fig.9 Step tracking control results for TVS

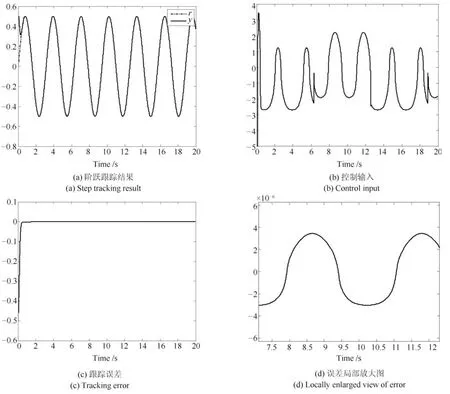
图10 SC-PD的正弦跟踪控制结果Fig.10 Sinusoidal tracking control results of the SC-PD

为了验证SC-PD控制器对时变系统(TVS)控制的有效性,使用与仿真实验6完全相同的5个时变参数,对非线性非仿射时变系统(32)进行控制实验,结果如图12所示.由图12可知,使用同一套SC-PD控制器参数对时变系统(32)进行阶跃跟踪控制实验,仍然获得了很好的控制效果,进一步表明了本文研究的SC-PD控制器对系统时变性和外部扰动具有很好的鲁棒性.

为了体现本文SC-PID控制器的创新性,下面分别使用在线自学习PID(包括PI)控制方法、在线自学习SMC控制方法以及ADRC方法进行对比分析.其中,在线自学习PID控制方法参照文献[16−17]进行仿真实验;在线自学习SMC控制方法参照文献[26]进行仿真实验;ADRC方法则使用在线自学习PID+ESO来实现.为了便于比较,四种控制器及其相关参数分别介绍如下:

1)SC-PI控制器:

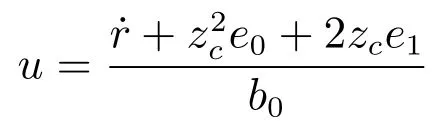
其中,zc=63[1−0.9 exp(−t)];

2)在线自学习SMC控制器:

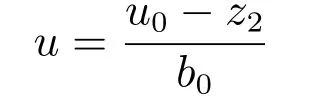
滑模函数:s=e1;

ESO增益:β01=1 000,β02=6 000;

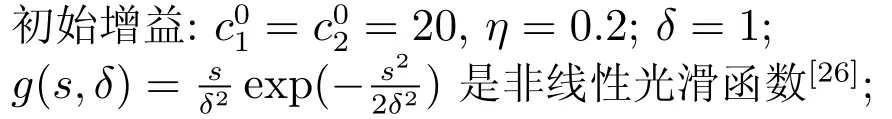
c1和c2在线更新算法如下:

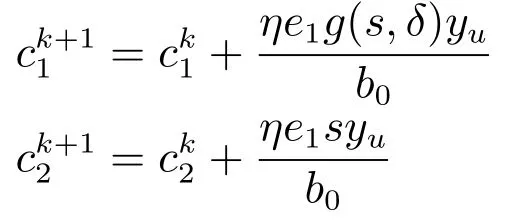
其中,yu为雅可比信息[26−27],下同.

3)在线自学习PI控制器:

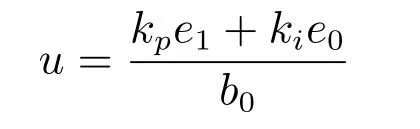
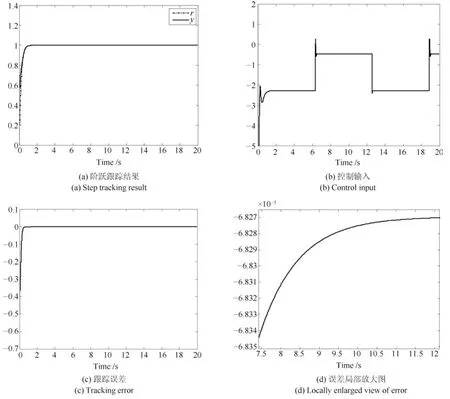
图11 SC-PD的阶跃跟踪控制结果Fig.11 Step tracking control results of the SC-PD

kp和ki在线更新算法为:

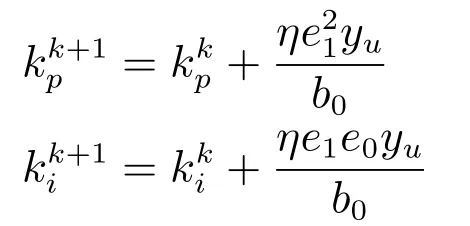
4)在线自学习ADRC:

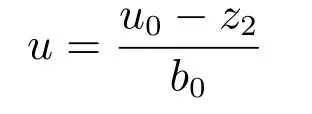
其中,

u0=kpe1+kie0,z2是总和扰动估计值;

ESO增益:β01=1 000,β02=6 000;

kp和ki在线更新算法为:

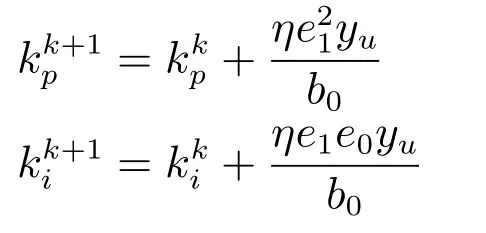
仿真实验10.一阶非仿射非线性系统的对比控制分析

针对被控系统(30),在初始状态完全相同、单位阶跃轨迹和外部扰动也完全相同,b0=1,分别使用SC-PI控制器、在线自学习SMC、在线自学习PI控制器以及在线自学习ADRC等四种控制器的控制结果如图13所示.由图13可知,在控制精度和抗扰动鲁棒性方面,SC-PI、SMC和ADRC相当,而自学习PI 控制器存在明显的差距.然而,与SMC和ADRC相比,SC-PI结构简单、计算量小,在实时性方面具有明显优势,由于自学习SMC和ADRC的抗扰动鲁棒性是依赖于ESO对总和扰动的估计来实现的,如果缺少ESO功能部件,与自学习PI控制器一样,它们的抗扰动能力会明显降低.

仿真实验11.二阶非仿射非线性系统的对比控制分析

针对被控系统(32),在初始状态完全相同、单位阶跃轨迹和外部扰动也完全相同.SC-PID、SMC、在线自学习PID以及在线自学习ADRC等四个控制器及其相关参数分别如下:

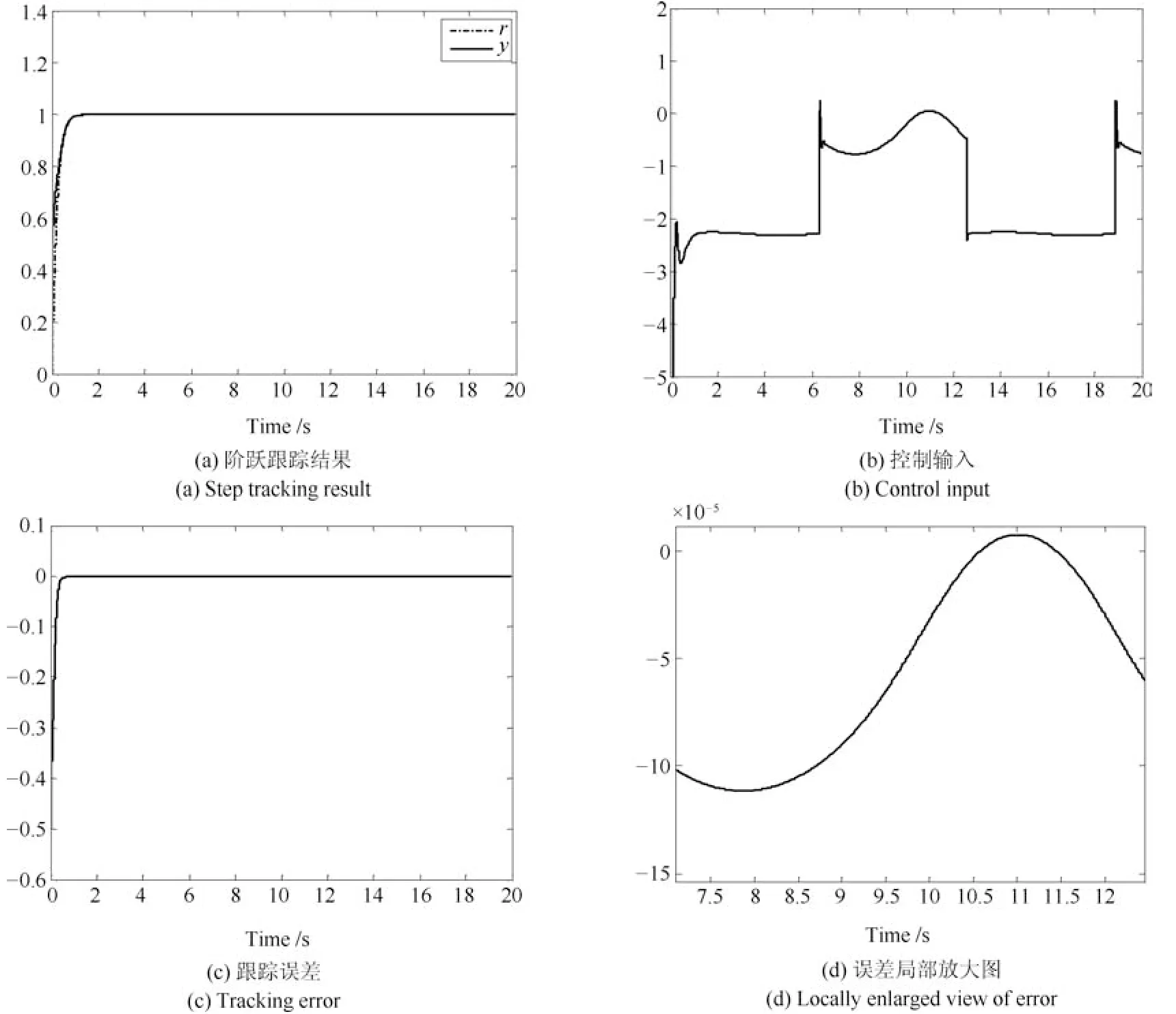
图12 时变系统的阶跃跟踪控制结果Fig.12 Step tracking control results for TVS

1)SC-PID控制器:

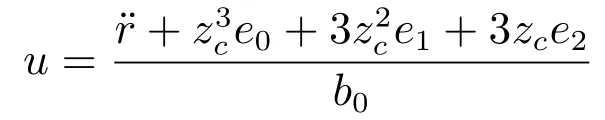
其中,zc=63[1−0.9 exp(−t)];

2)SMC控制器:

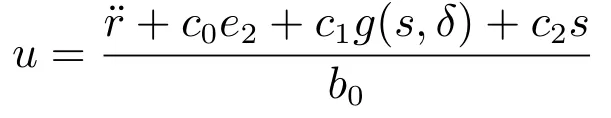
且

3)在线自学习PID控制器:

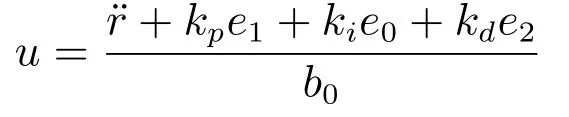
在线更新算法如下:

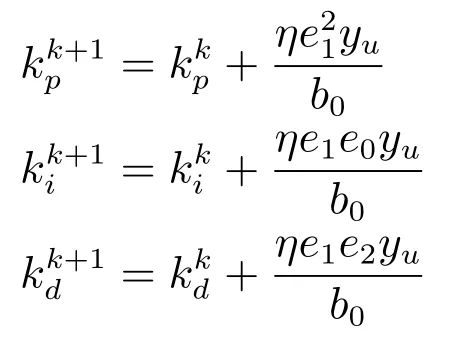
其中,yu为雅可比信息[16−17],下同.

4)在线自学习ADRC:

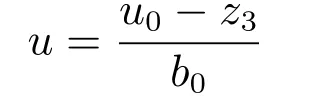
其中,

u0=kpe1+kie0+kde2,z3是总和扰动估计值;

ESO增益:

β01=1 000,β02=6 000,β03=30 000;

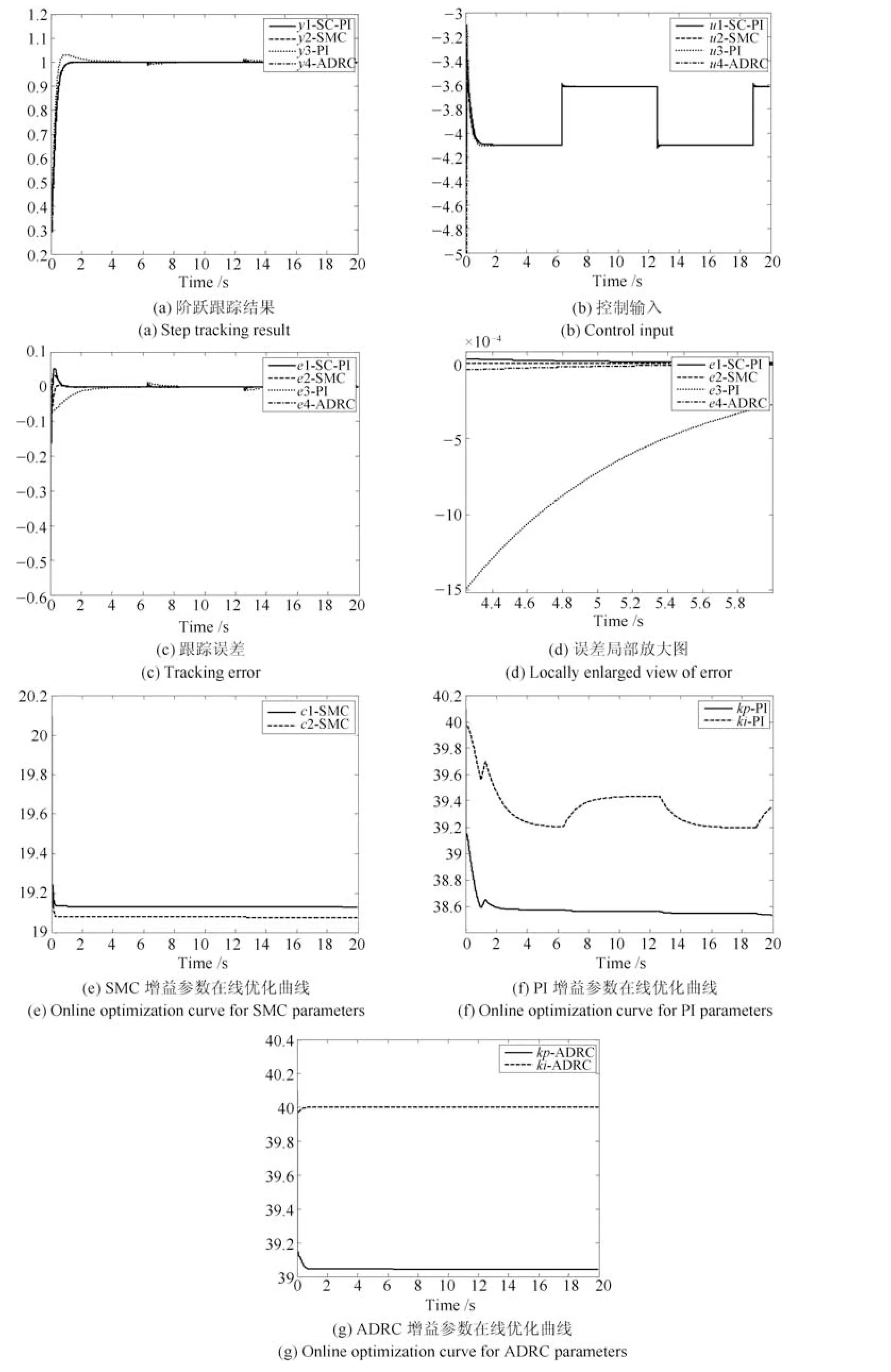
图13 四种控制器的控制结果Fig.13 Control results of the four controllers

在线更新算法如下:

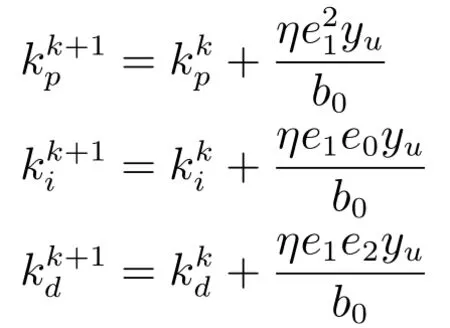
针对非线性非仿射不确定被控对象(32),SCPID、SMC、在线自学习PID以及在线自学习ADRC等四个控制器的仿真结果如图14所示.

由图14可知,在线自学习PID和ADRC都存在明显的超调和波动现象,而且由动态进入稳态的过渡过程时间较长.由图14(h)的外部扰动可知,外部扰动在6.284 s时刻发生从+1到−1的跳变.假设扰动出现时刻,四种控制系统都处于稳定状态,根据图14(d)和图14(e)的误差局部放大图可知,与其他三种方法相比,SC-PID具有高得多的稳态精度(稳态绝对误差不超过5×10−8),而SMC、自学习PID以及ADRC的稳态精度相当(绝对误差分别不超过2.8×10−3、5.1×10−3、2.4×10−3).显然,SC-PID控制方法的稳态精度是现有其他方法的十万倍.

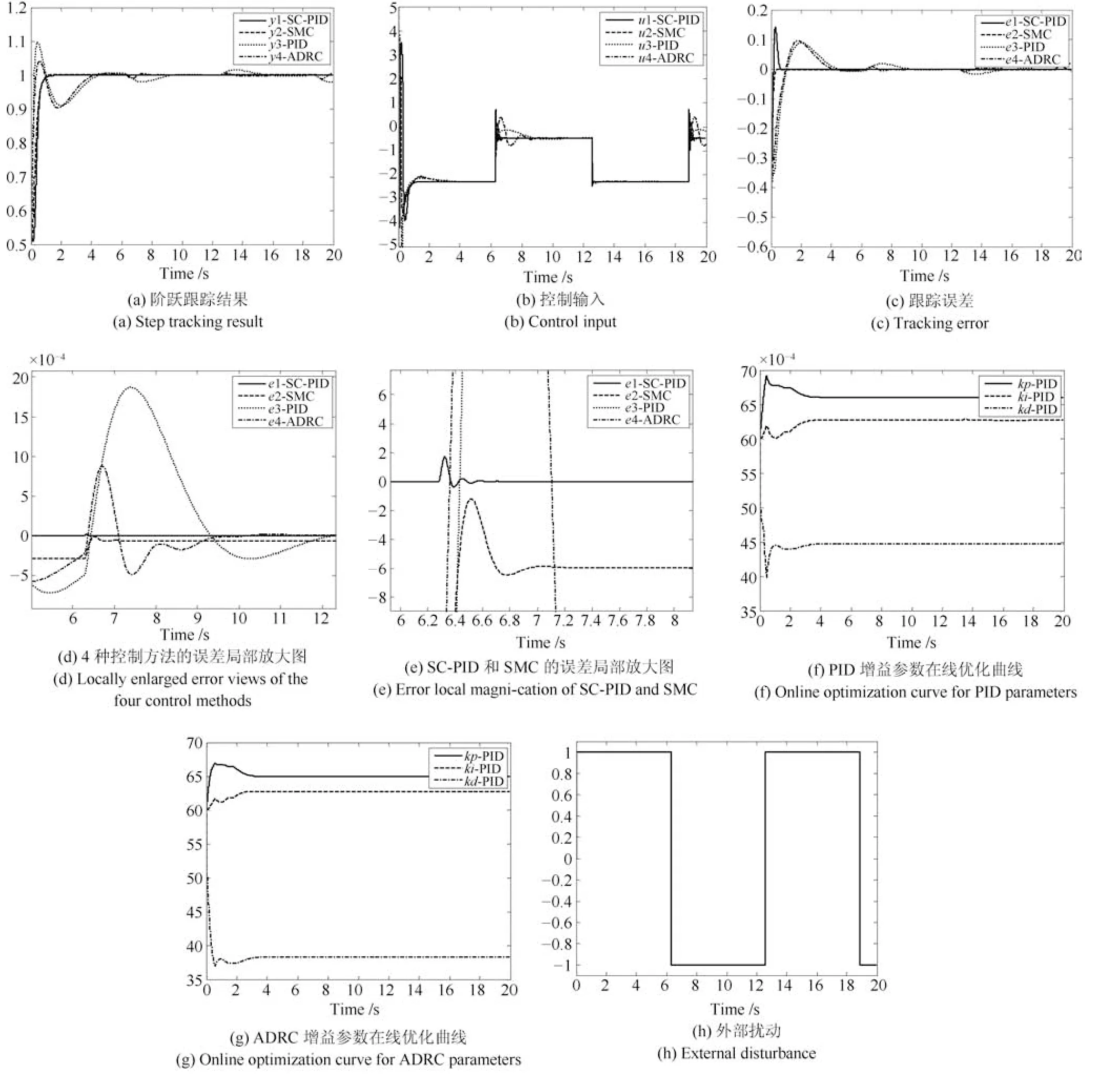
图14 四种控制器的控制结果Fig.14 Control results of the four controllers

此外,当扰动出现以后,与其他三种方法相比,SC-PID在抗扰动能力方面也同样具有明显的优势,只需要约0.47 s即可快速恢复到稳定状态;而ADRC则需要约3.22 s才能恢复到稳定状态;自学习PID则需要约5.72 s才能恢复到稳定状态.尽管SMC抗扰动能力较强,而且恢复时间只需要0.82 s左右,然而却一直存在约−6×10−4的固有静态偏差.

通过实验结果的对比分析可知,与现有的PID、SMC和ADRC等三种控制方法相比,本文提出的SC-PID控制方法在响应速度、稳态精度以及抗扰动能力等方面都具有明显的优势.

5 结论

本文提出的SC-PID控制器的主要思想是:

1)借鉴了韩京清先生的思想:将系统动态不确定性(包括模型不确定性和参数不确定性)以及外部扰动作为总和扰动,使非线性不确定系统转化为线性不确定系统,因而淡化了线性与非线性、确定与不确定性、时变与时不变性、耦合与非耦合、仿射与非仿射等系统分类的概念;

2)借鉴了跟踪微分器的模型思想,提出了SCPID控制器模型,进而将一个非线性不确定系统或其等价的线性不确定系统的闭环控制系统转换为总和扰动反相激励下的误差动态系统;

3)分别从复频域和时域分析了由SC-PID控制器组成的闭环控制系统不仅具有大范围稳定性能,而且SC-PID还具有良好的抗总和扰动鲁棒性,因而从理论上保证了SC-PID(包括SC-PI 和SC-PD)控制器的有效性.

为了有效解决快速性与超调之间的矛盾,提出了自适应速度因子模型,从而使SC-PID成为ASCPID.系列仿真实验不仅验证了SC-PID控制方法的有效性,而且也验证了理论分析的正确性.此外,还与现有改进型PID、改进型SMC以及ADRC进行了比较分析,进一步表明了SC-PID在模型结构、响应速度、控制精度以及抗扰动鲁棒性等方面的突出优势.本文研究的不依赖于被控对象模型的SC-PID控制器的主要特色是:不仅控制器结构简单(只有一个速度因子)、计算量小(不需要在线优化增益参数、不需要扰动观测器实时估计扰动状态)、响应速度快、控制精度高、抗扰动能力强、无超调、无振荡、无抖振,而且对系统内部不确定性、参数时变性以及外部扰动都具有很好的鲁棒性等突出优势.SC-PI、SC-PID和SC-PD控制器的增益整定规则分别为现有运行中PI、PID和PD控制器的增益整定结果进行技术评估与技术升级提供了科学的理论依据.