结构辨识和参数优化协同学习的概率TSK 模糊系统

顾晓清 倪彤光 张聪 戴臣超 王洪元

模糊推理系统(Fuzzy inference system,FIS)以模糊集合和模糊推理为基础,能够将自然语言直接转译成计算机语言,使得机器具有表达模糊语意的能力,目前被广泛应用在时间序列分析、工业控制和故障诊断等方面[1−2].相比大多数智能模型,FIS的优势在于:1)FIS具有很强的面向不确定系统的构建能力,能模拟人类专家知识和推理的不确定性;2)不像SVM和神经网络等被视为一个黑箱,FIS具有良好的基于规则的解释性;3)FIS具有强大的学习能力,能利用模糊逻辑较强的结构性知识表达,也可以像神经网络等模型一样利用数据集信息对模型参数进行优化学习.由Takagi,Sugeno和Kang 提出的Takagi-Sugeno-Kang (TSK)模糊系统,又称TSK模糊模型,因其结构简单和逼近能力强,是一种常用的FIS工具[2].TSK模糊系统使用具有解释性的“IF-THEN”规则来定义系统的规则库,规则库的构建工作由2部分组成:规则结构的辨识和规则参数的优化.规则结构的辨识指为系统的输入空间找到合适的模糊划分;规则参数的优化则指确定模糊规则前件和后件的参数.其中,选择合适的模糊规则数是结构辨识的核心工作[3].模糊规则数过多会导致模糊系统复杂化,易产生过拟合现象;模糊规则数过少则导致系统逼近性能不佳.

目前,确定模糊规则数最简单的方法是基于网格的输入空间划分法.特征数是d的数据集,如使用固定m网格的输入空间划分法,共提取到md条模糊规则数.显然这一方法不适用于高维数据[4].确定模糊规则数的另一类常用方法是聚类算法[5−6],聚类法TSK模糊系统的一大优点是能获得较小规模的规则数,但模糊规则数往往需要预先设定,如文献[5−7]使用交叉验证的方法获得模糊规则数的最优值.虽然一些聚类有效性指标如Xie-Beni指标和Mountainpotential 指标等能用于聚类数的选择,但这些有效性指标用于确定模糊规则数时往往效果不佳[8].此外,聚类法TSK模糊系统在优化模糊规则的前件和后件参数时往往分阶段计算,这种学习策略的优点是时间复杂度相对较低,但其存在一个严重的缺陷:无法捕捉输入空间和输出空间之间的内在联系,因此得到的TSK模糊系统的逼近性能往往达不到最优.为解决这一问题,近年来一些学者开始研究前件和后件参数的联合学习方法,如文献[9]使用迭代线性支持向量回归机来联合学习前件和后件参数,文献[10]建立了前件和后件参数联合学习的贝叶斯推理模型,并使用Metropolis-Hastings(MH)采样方法求解参数的最优解.然而这两个算法仍需事先设定模糊规则数.

众所周知,模糊理论和概率模型是常用于描述复杂问题不确定的两类方法.但两者的侧重点不同:模糊理论能较好地描述自然语言的不确定性,即语义的不确定性;概率模型能较好地描述由系统固有偶然性或变异性带来的随机不确定性,即系统性能或预测结果的不确定性[11].Zadeh 在文献[11]中首次提出了“概率和模糊互补多于竞争”这一思想,认为两者通过协同学习可以提高系统的性能.受这一思想启发,本文提出了一种结构辨识和参数优化协同学习的概率TSK模糊系统(Probabilistic TSK fuzzy system,PTSK).PTSK的核心思想是将数据的输入/输出空间、系统结构和规则参数作为一个整体来考虑,并基于概率理论使用概率模型来构建模糊回归系统.不借助于专家经验,基于最大后验概率估计(Maximum-a-posteriori,MAP),PTSK使用粒子滤波方法[12]同时得到模糊规则数、规则前件/后件参数的最优解.PTSK模糊系统的优点有:1)以一种协同学习的形式构建了基于概率模型的TSK模糊系统.该系统兼具统计学和模糊逻辑的优点,能有效处理非线性回归问题.2)不同于传统聚类法TSK模糊系统使用“黑盒”策略(如网格搜索法)优化模糊规则数的方法,PTSK无需任何专家经验,使用粒子滤波方法能自动学习模糊规则的所有参数.3)PTSK充分挖掘数据集的整体特征,同时考虑输入空间和输出空间对模糊规则参数的影响.实验结果表明PTSK兼具强解释性和良好逼近性能的特点.

1 相关工作

1.1 TSK模糊系统基本概念

TSK模糊系统规则库中的第k个模糊规则可用以下形式表示:

其中x1,x2,···,xd是输入向量x的d维分量,Ak(Ak=[Ak1,Ak2,···,Akd]T)是输入空间的模糊子集,K是模糊规则数.令vk=[vk0,vk1,···,vkd]T,=[1,xT]T,模糊规则THEN部分的fk(x)可以写成:

令µk(x)是第k条模糊规则的隶属度函数,其值可由各维对应的隶属度值通过合取操作获得,

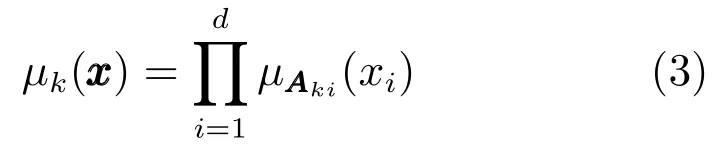
若引入高斯函数作为隶属度函数,式(3)中µAki(xi)可表示为:

其中隶属度函数的中心cki和方差δki被称为模糊规则的前件参数.TSK模糊系统的实值输出ˆy为:

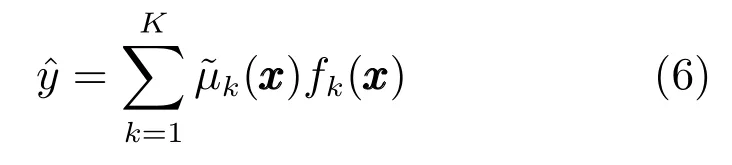
1.2 聚类法TSK模糊系统的参数学习

表1比较了聚类法TSK模糊系统中常用的规则前件/后件参数学习方法.系统中每一个聚类划分转化为一条模糊规则.此时式(5)中的隶属度函数中心ck为聚类中心,方差δk可由下式计算得到:

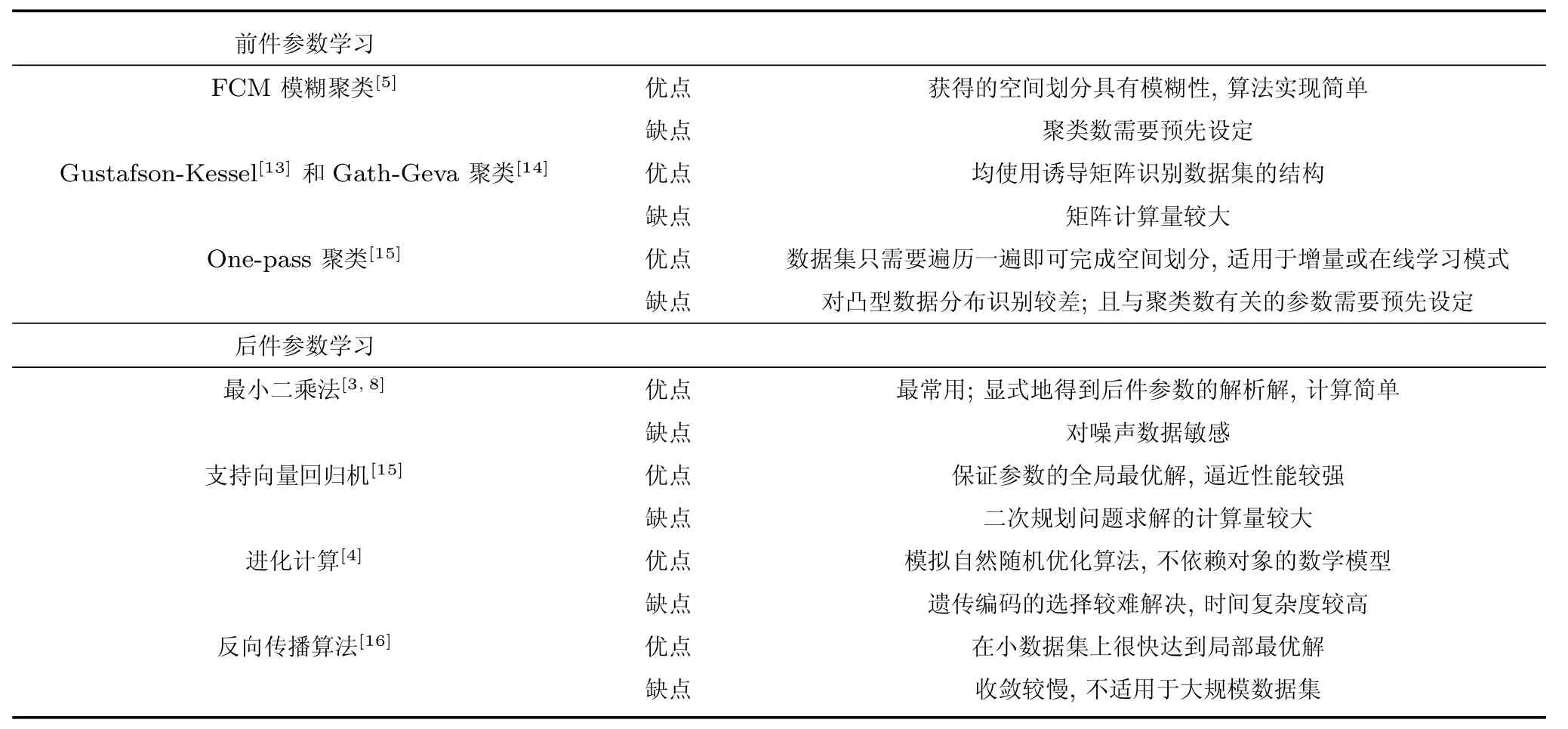
表1 聚类法TSK模糊系统中常用的模糊规则前件/后件参数学习方法Table 1 The common learning methods for the antecedent/consequent parameters in the clustering based TSK fuzzy system

其中Nk是第k个聚类中样本的个数.若采用最小二乘法求解后件,TSK模糊系统的目标函数可写成:

其中φ(x)=[(µ1(x)xe)T,···,(µK(x)xe)T]T,xe=[1,xT]T.后件参数矩阵V则可通过下式求解得到:

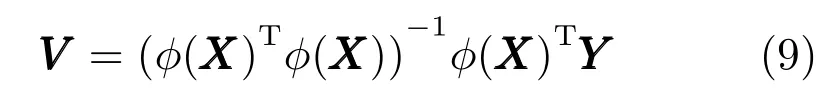
2 概率TSK 模糊系统(Probabilistic TSK Fuzzy System,PTSK)

2.1 PTSK联合概率模型

给定输入数据集X={xi,i=1,2,···,N,xi∈Rd}和对应的输出集Y={yi,i=1,2,···,N,yi∈R},PTSK关于输入/输出数据、规则数和前件/后件参数的联合概率表示为p(X,K,U,C,Y,V),其中4个待优化参数分别是模糊规则数K,聚类中心矩阵C,模糊划分矩阵U和后件参数矩阵V.根据贝叶斯概率,p(X,K,UU,C,Y,V)可以表示为:

式(10)由4 个因子构成.下面对这4个因子展开叙述.

1)p(X|K,U,C,Y,V):聚类法TSK模糊系统中每一个聚类对应一条模糊规则.此时,条件似然p(X|K,U,C,Y,V)仅与聚类数K,模糊隶属度矩阵U和聚类中心矩阵C有关,等价于p(X|K,U,C).PTSK假设xn的先验是K个正态分布的乘积,正态分布的中心为聚类中心ck,协方差是其模糊隶属度分量unk构成的单位阵,即

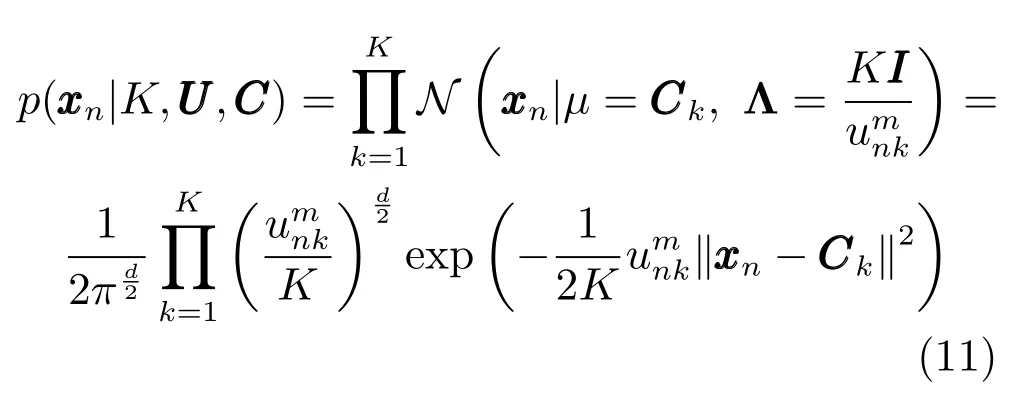
其中m是模糊指数.输入数据X中的每个样本都满足独立同分布,条件似然p(X|K,U,C,Y,V)可表示为全部样本的正态分布先验的乘积,即

2)p(U|K,C,Y,V):模糊划分矩阵U仅与聚类个数K和聚类中心矩阵C有关,且每个样本对应的模糊隶属度相互独立,因此U的条件似然可以写成狄利克雷(Dirichlet)分布是一种多变量连续概率分布,其每个分量均大于0且每一维度之和为1.文献[17]使用狄利克雷分布来构造模糊聚类的模糊隶属度.拉普拉斯(Laplace)分布较正态分布在中心点处有较高的峰度,文献[18]使用拉普拉斯分布来提高聚类模型的稀疏性.因此,PTSK在模糊划分矩阵U的条件似然中同时考虑狄利克雷和拉普拉斯分布,p(U|K,C,Y,V)可以写成:

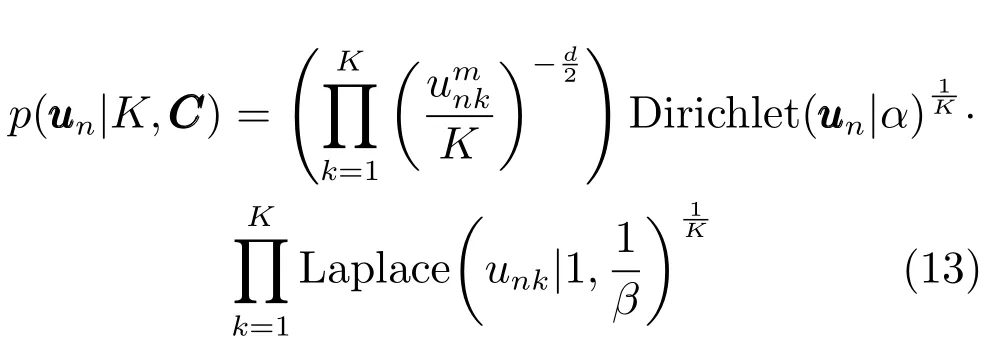
其中α=[α1,α2,···,αK]T是狄利克雷参数,B(α)是一个正常数.第3项K维拉普拉斯分布的形式为:

其中β是拉普拉斯分布的尺度参数.因为unk在[0,1]之间且满足化简后其值在上式中被消去.对式(13)∼(15)进行整理,p(U|K,C,Y,V)可以写成以下形式

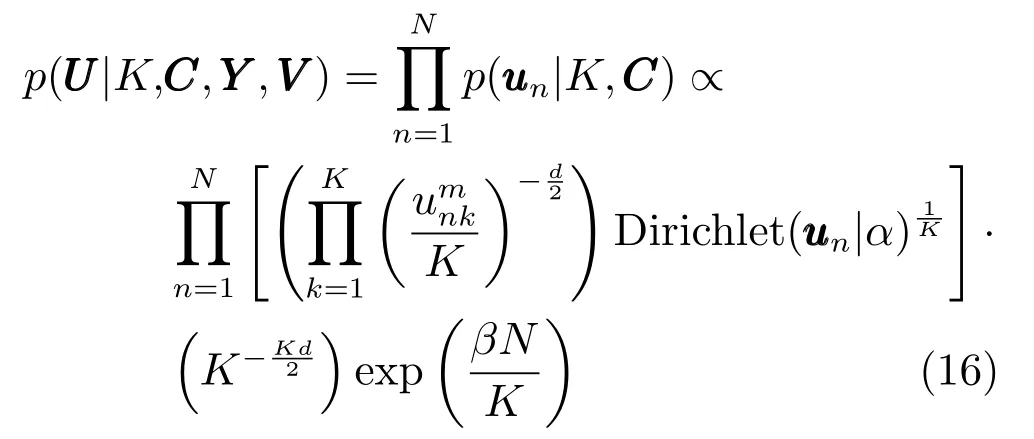
3)p(C,Y,V|K):在给定模糊规则数的情况下,PTSK在条件似然p(C,Y,V|K)中考虑系统在K条模糊规则上的平均估计误差,即

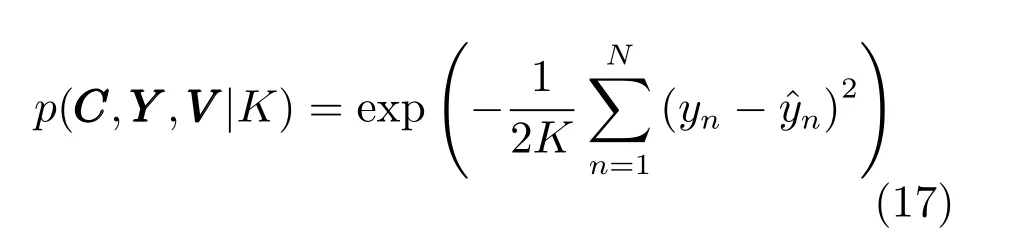
4)p(K):模糊规则数是正整数,其服从离散分布.其分布可采用两种方法:一种是假设模糊规则数服从离散均匀分布,即p(K)=discrete(K)=1/l,其中l是区间内离散值的个数.此时模糊规则数的选取等价于网格搜索法.另一种是使用泊松过程或泊松分布[12].因为离散均匀分布的区间上界不易设定,本文设定模糊规则数的先验分布服从泊松分布:

其中λ是形状参数,参照文献[19],λ=lgN.

将式(12),(16),(17)和(18)相乘,得到PTSK关于数据、规则数和前件/后件参数的联合概率模型:

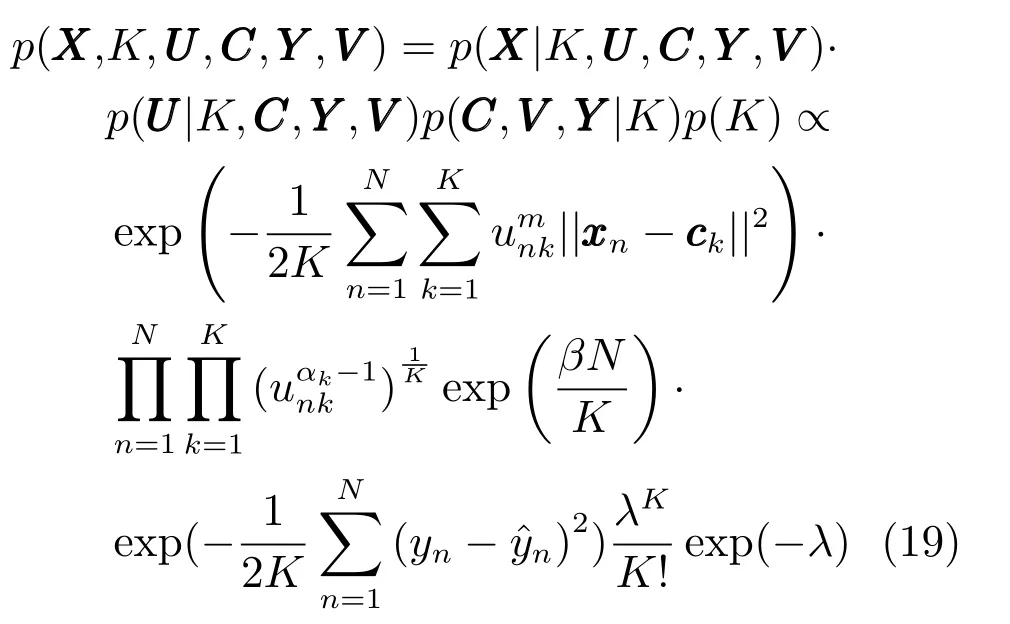
对上式取自然对数,可以得到PTSK的目标函数:

从式(19)和(20)可以看成,PTSK将数据的输入/输出空间、规则数的识别和前件/后件参数的优化视作一个整体,得到的规则数和前件/后件参数一定是相互依赖、密切相关的.当式(20)联合概率模型达到MAP值时,PTSK中参数{K,U,C,V}同时得到最优解.

2.2 PTSK结构辨识和参数优化的协同学习

粒子滤波方法是一种序贯蒙特卡罗方法,使用带权值的随机粒子按照序贯重要性采样方法递归估计状态变量的后验概率分布.粒子滤波方法还具有噪声容忍性强和模型初始状态不敏感的优点.PTSK采用粒子滤波方法求得式(20)的最大后验估计.PTSK结构辨识和参数优化的协同学习示意图如图1所示.

从图1可以看出,PTSK结构辨识和参数优化的协同学习由一系列迭代过程构成.在算法初始化阶段,PTSK创建一组带权重的离散粒子WDP[r]={{K,U,C,V},ll}T(r=1,2,···,P),其中ll是式(20)对应的目标函数的值,P是粒子数.PTSK设置各粒子模糊规则数K的初值为1,模糊隶属度矩阵U的元素初值为ui1=1(i=1,2,···,N),聚类中心矩阵C的元素初值ci1为输入数据X的均值.PTSK创建候选最优粒子集CAND,设置CAND[1]=WDP[1].下面详细介绍第n次迭代过程,其主要由4个步骤构成:

1)采样.使用式(18)对模糊规则数K∗进行采样,其泊松分布的均值为当前规则数K.如果新采样的模糊规则数K∗小于当前规则数K,从聚类中心矩阵C中随机选择K∗个中心作为当前聚类中心矩阵;如果新采样的模糊规则数K∗大于当前规则数K,则保留当前聚类中心矩阵CC,并使用d维拉普拉斯分布采样K∗−K个新聚类中心

其中拉普拉斯分布的位置参数e是输入数据X的均值,γ是尺度参数.经过大量实验,γ取值为5.

2)参数优化.这一步骤的工作是根据采样得到的模糊规则数K∗对参数{U,C,V}进行优化.

a)优化模糊隶属度矩阵U.随着模糊规则数K的变化,模糊隶属度矩阵U也相应变化.由于对模糊隶属度的取值无先验知识,PTSK假设模糊隶属度服从平坦型狄利克雷(Flat Dirichlet)分布[20],此时狄利克雷分布参数α中各分量为1.狄利克雷分布能保证所采样的模糊隶属度元素满足unk≥0且将其作为约束条件改造式(20)可得:

其中ηn是拉格朗日乘子.上式得到极值的必要条件为∂J/∂unc=0,可得unc的解析解:

当前隶属度函数的宽度矩阵δ和后件参数矩阵V可以分别通过式(7)和式(9)计算得到.

b)优化聚类中心矩阵C.固定模糊规则数K和模糊隶属度矩阵U,此时式(20)得到极值的必要条件为∂J/∂cki=0,可得cki的解析解:

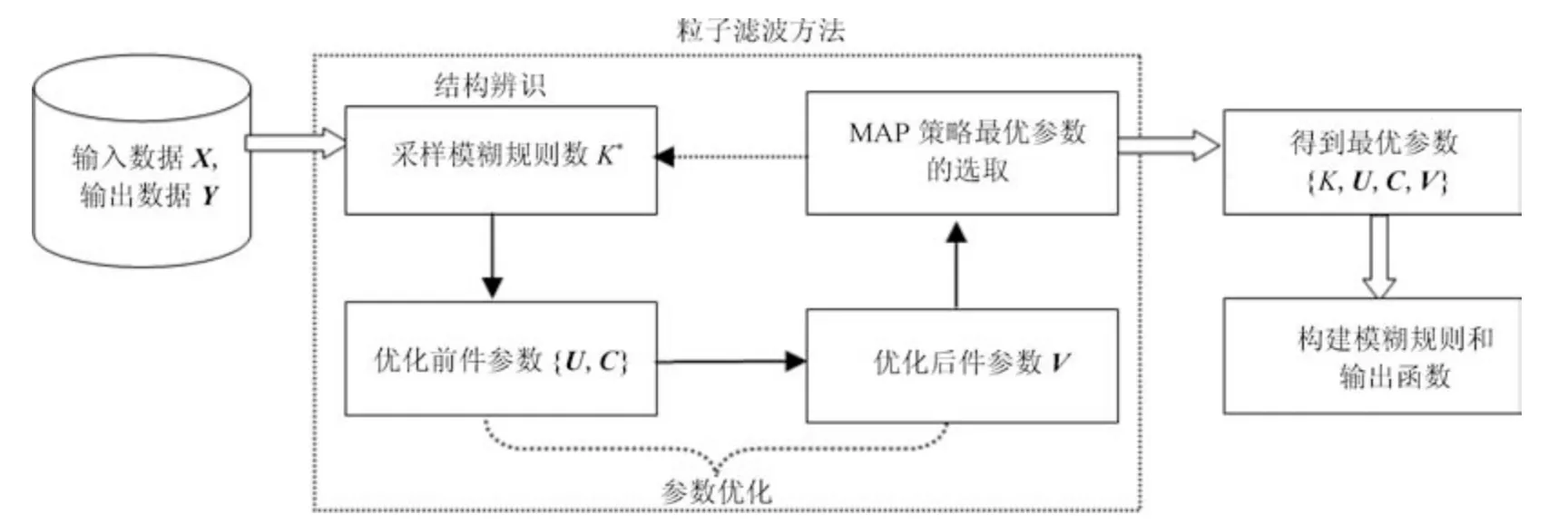
图1 PTSK结构辨识和参数优化的协同学习示意图Fig.1 The diagram of simultaneous learning of structure identif cation and parameter optimization in PTSK

c)优化后件参数矩阵V.优化模糊划分矩阵U和聚类中心矩阵C后,此时式(20)得到极值的必要条件为∂J/∂V=0,可得V的解析解的形式与式(9)相同.

d)计算粒子对应的目标函数值.在优化了每个粒子对应的参数{K,U,C,V}后,每个粒子对应的目标函数值ll可通过计算式(20)得到.

3)粒子更新.检查粒子集WDP中的每个粒子的ll值能否提高当前模糊规则数对应的目标函数值,如果是,则将该粒子替换当前模糊规则数的候选最优粒子CAND[K],并加入到粒子集CAND中,如果不是,则保留CAND[K],即

然后使用WDP和CAND构建粒子集PS,

4)权重计算和重采样.为了减少粒子退化的影响,PTSK根据粒子权重执行重采样操作,更新粒子集WDP.每一个粒子的权重值wi的计算式为

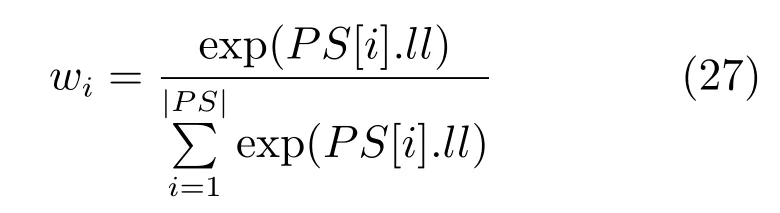
其中|PS|表示粒子集PS中粒子的个数.每个粒子的重采样概率与权重值wi成正比,从粒子集PS中重采样P个粒子并使用它们更新粒子集WDP.这样WDP中权重小的粒子被剔除掉,权重大的粒子被保留,甚至被多遍复制.最终,在经过若干次迭代后,粒子集WDP中最大ll值对应的粒子的参数{U,C,V}为PTSK模糊系统的最优参数.

2.3 算法描述和分析

首先给出PTSK模糊系统的构建算法描述,如算法1所示.

在重采样步骤中,相比传统粒子滤波方法[21]仅使用固定规模的粒子集WDP,PTSK使用不固定规模的粒子集PS,PS粒子集由2部分构成:粒子集WDP和CAND,其中CAND由采样得到的不同模糊规则数的候选最优粒子构成,粒子数不固定.粒子集CAND的作用是进一步减小粒子退化的影响,加快算法的收敛.

接下来,我们分析PTSK模糊系统的收敛性.在实际应用中,粒子数的规模有限,系统需要在收敛速度和系统性能之间进行平衡.因此,PTSK在算法的终止条件上除了设置最大迭代次数外,还计算当前目标函数值与上一次迭代目标函数值之间的差值,若其值小于阈值ε,则统计其次数.当累计次数超过设定值miter时,算法终止.因为随着迭代次数的增加,模糊规则数趋于固定,规则的前件/后件参数也仅在最优值附近微调,此时使用式(17)计算全部规则上的平均估计误差几乎不变,系统的性能趋于稳定.因此,依据文献[22]粒子滤波方法求解系统静态参数可得局部最优解的结论,算法1也可保证所得模糊规则数和规则前件/后件参数的最优解是局部最优解.最后,我们分析PTSK模糊系统的时间复杂度.由算法1步骤可知,PTSK模糊系统的时间复杂度主要集中在对参数{U,C,V}的优化部分.使用式(23)优化模糊隶属矩阵U的时间复杂度是O(NK).使用式(24)优化聚类中心ccck的时间复杂度是O(NK2(d+1)).基于平均估计误差的模糊规则后件参数的时间复杂度是O(N3).因此,算法1执行单次迭代的时间复杂度为O(P(NK+K2N(d+1)+N3)),其中N,K,d和P分别表示训练样本个数,模糊规则数,样本维数和粒子数.

算法1.PTSK模糊系统的构建

//初始化

1)创建粒子集WDP,设置K=1,分别使用式(21)和(23)初始化c和u;

2)创建粒子集CAND,设置CAND[1]=WDP[1];

3)设置迭代次数t=1,r=1;

Repeatt=t+1;

Repeatr=r+1;

//采样模糊规则数K

4)用式(25)更新K∗;

//优化参数{U,C,V}

5)更新WDP[r].K=K∗;

6)使用式(23)计算WDP[r].U;

7)使用式(24)计算WDP[r].C;

8)使用式(9)计算WDP[r].V;

9)使用式(20)计算WDP[r].ll;

//粒子更新

10)使用式(25)得到候选最优粒子集CAND;

11)构建粒子集PS={WDP,CAND};

Untilr >P

//权重计算和重采样

12)使用式(27)计算PS中粒子的权重值wi;

13)以wi为重采样概率,在PS中重采样P个粒子,并更新粒子集WDP;

Untilt ≥tmax或者

14)选择CAND中ll值最大的粒子,得到{K,U,C,V}最优解;

//构建模糊规则

15)使用最优解{K,U,C,V}构建模糊规则,并由式(6)得到输出函数.

3 实验研究

为了验证本文方法的有效性,本节将通过28个回归数据集对PTSK模糊系统进行分析与验证.实验安排如下:第3.1节对数据集和实验的设置进行了介绍;第3.2节分析了PTSK和7 种对比算法在28个数据集上的实验结果;第3.3节对实验结果进行了统计分析;最后给出PTSK收敛性和参数敏感性分析.

3.1 实验设置

表2列出了实验中使用的28个回归数据集的基本信息.mexihat、abalone、housing、mg 和bodyfat来自LIBSVM数据集[23],gc-s、gc-x 和gc-p数据集来自文献[6],其余数据集来自KEEL数据集[24].实验比较了两类共7 种回归算法,一类是TSK模糊系统:L2-TSK-FS[5],TSK-IRL-R[25],MOGULTSK-R[26]和B-ZTSK-FS[10].另一类是经典的回归算法:WM-R[27],ENSEMBLE-R[28]和PSVR[29].L2-TSK-FS,B-ZTSK-FS,PSVR 和PTSK使用MATLAB2016b实现;其余方法使用KEELtoolbox软件实现[24].实验中各算法参数的设置如表3所示,7 种对比算法的参数设置均使用相应文献的默认设置.参数的选取使用5重交叉验证的方法.实验采用3个评价指标:1)均方误差MSE(Mean squared error)和方差;2)平均训练时间;3)TSK模糊系统的平均规则数.同时,为了使得性能对比更具有统计意义,本文采用无参统计学方法中的Friedman 检验[30]和Host事后检验[31]进行统计测试.本文全部实验在Intel i7-3770 CPU 3.4 GHz,16 GB RAM,Windows 7 的环境下执行.

表2 数据集基本信息Table 2 Basic information of datasets

3.2 实验结果分析

实验比较了PTSK和另外7 种回归算法在28个数据集上的实验结果,表4和表5分别显示了各算法的MSE(标准差)和平均训练时间,表6比较了6种TSK模糊系统得到的平均模糊规则数.

1)从表4可以看出,PTSK在所有数据集上取得了令人满意的MSE值,PTSK在28个数据集上胜出17 次,ENSEMBLE-R、PSVR、TSK-IRL-R和WM-R 各胜出2、5、3和1次.L2-TSK-FS和BZTSK-FS采用网格搜索法求得模糊规则最优解,但设定合适的规则数搜索区域较困难,因而L2-TSKFS和B-ZTSK-FS的平均MSE值不理想.由此可知挖掘数据输入空间和输出空间内在联系对TSK模糊系统的性能有着重要的影响,亦说明PTSK采用的基于概率模型的结构辨识和优化参数的协同学习机制有利于找到合适的模糊规则数.

2)从表5可以看出,8种回归算法中MOGULR 和TSK-IRL-RPTSK训练时间最长,PSVR 和L2-TSK-FS训练时间最短,PTSK在样本规模较大的数据集上训练时间也较长.但由表3可以看出,PTSK需要寻优的参数只有1个,而L2-TSK-FS需要寻优的参数有3个,因此,在实际应用中L2-TSKFS在训练时间上并不具备优势.PSVR 是支持向量机算法,虽然训练时间较短,但它不具有FIS的语义性和解释性.另外,TSK-IRL-R,MOGUL-TSK-R,WM-R 和ENSEMBLE-R 通过KEEL toolbox平台实现,该平台使用Java 软件实现.由于相同代码在MATLAB平台的运行时间比在Java 平台的时间时间慢大约6倍左右[32],因此,ENSEMBLE-R和WM-R 在训练时间上也并不比PTSK具有优势.

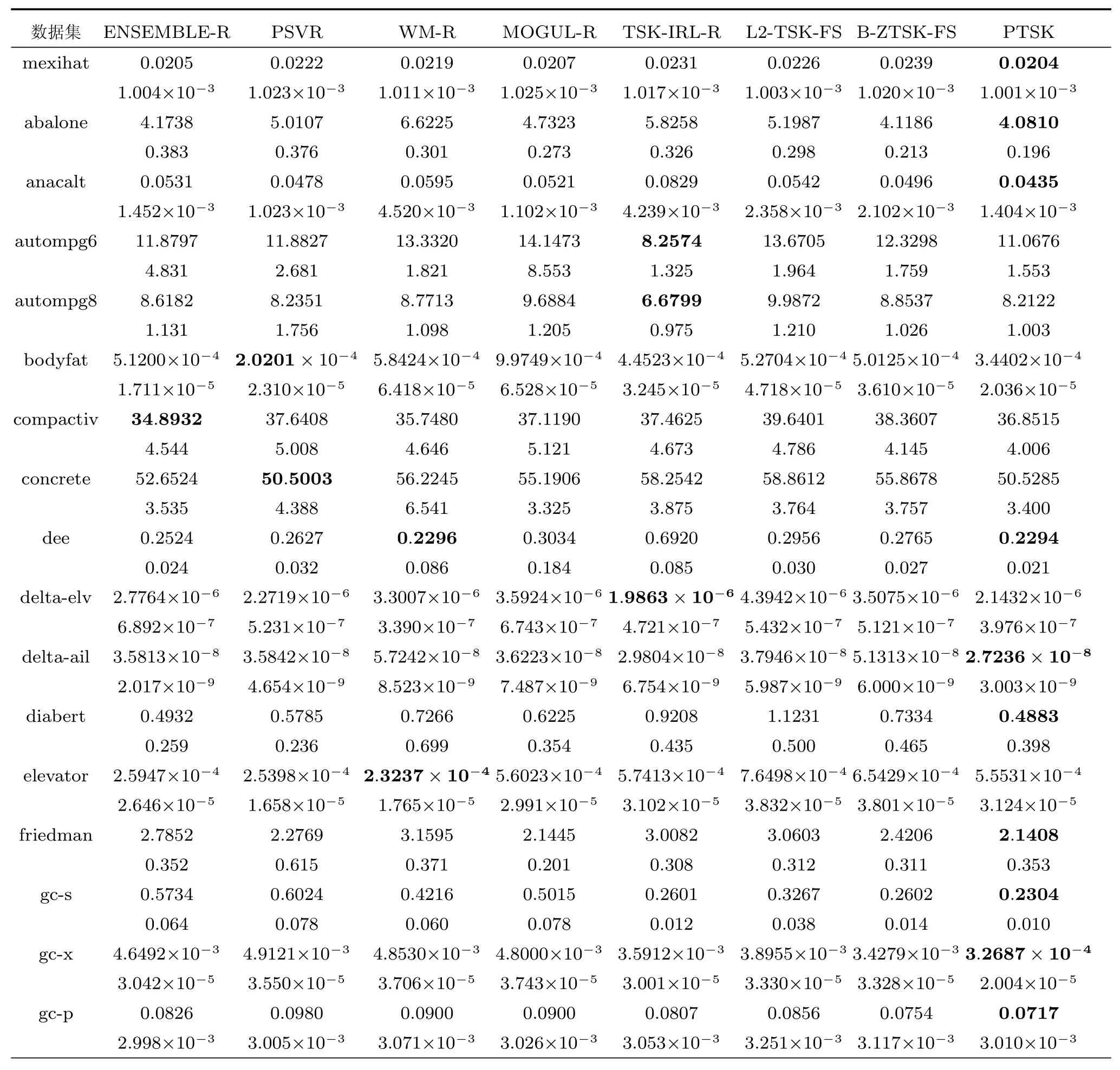
表4 8种算法在28个数据集上的MSE(标准差)比较Table 4 MSE(Standard deviation)comparison of 8 algorithms on 28 datasets

表4 8种算法在28个数据集上的MSE(标准差)比较(续表)Table 4 MSE(Standard deviation)comparison of 8 algorithms on 28 datasets(Continued table)

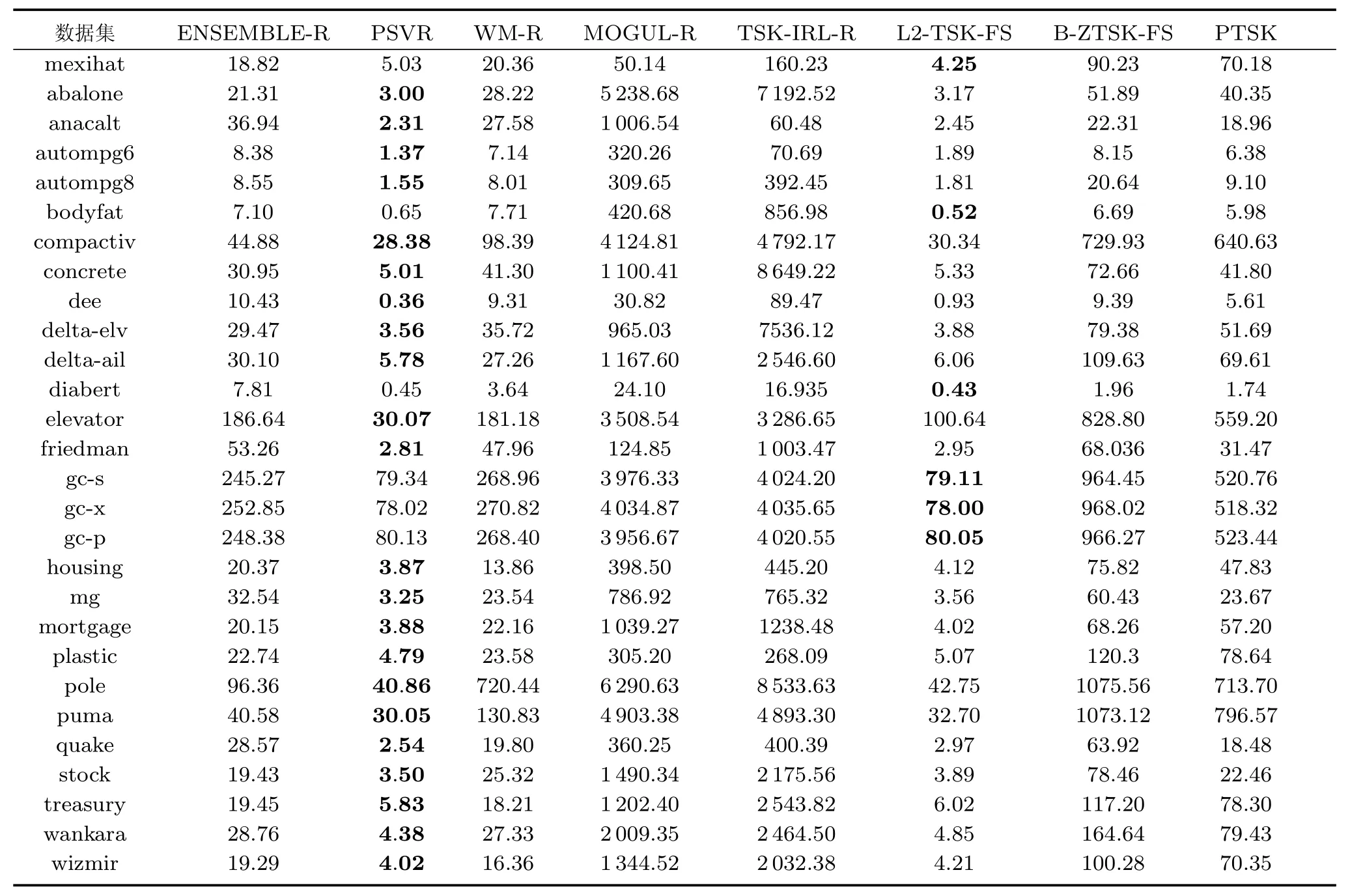
表5 8种算法在28个数据集上的平均训练时间(s)的比较Table 5 Comparison of the average training time (s)of 8 algorithms on 28 datasets

表6 6种TSK模糊系统在28个数据集上的平均模糊规则数比较Table 6 Comparison of the average number of fuzzy rules of six TSK fuzzy systems on 28 datasets

3)从表6可以看出,与对比的5种TSK模糊系统相比,PTSK仅需少量的模糊规则就能取得良好的分类效果,说明PTSK有较强的解释性.尽管B-ZTSK-FS使用MH 采样方法能够同时学习模糊规则的前件和后件参数,但是该方法不能自动学习模糊规则数,因此B-ZTSK-FS构建的模糊规则数多于PTSK.

图2显示了PTSK在mexihat数据集上某一折的实验结果,图3对应显示了PTSK在mexihat数据集上得到的4条模糊规则的模糊集示意图.从图2可以看出,PTSK取得了良好的逼近性能.我们知道,规则库的解释性与模糊规则数有关,另一方面,规则库的解释性也与模糊子集的清晰度有关.从图3可以看出模糊集具有语义解释性,由此可得对应的4条模糊规则也具有较高的解释性.

3.3 算法分析

3.3.1 参数敏感性实验和收敛性分析

首先对PTSK的参数敏感性进行分析.稀疏因子β使用5折交叉验证的方法得到最优值.实验设置β的搜索范围是{1,2,···,8}.由于篇幅所限,表7 显示了在mexihat,elevators,bodyfat和wizmir 数据集上β参数对MSE 指标和模糊规则数的影响.

图2 PTSK在mexihat数据集上的实验结果Fig.2 Experimental results of PTSK on mexihat dataset

由表7 的结果可以看出:1)稀疏因子β对模糊规则数起到了决定性作用.对于绝大多数数据集而言,β值越大获得的模糊规则数越少;反之,β值越小获得的模糊规则数越大.只有极个别数据集上的模糊规则数受β值的影响不大,其原因是该数据集在模糊空间分布较紧密且聚类划分结果清晰.2)PTSK模糊系统的回归性能与模糊规则数密切相关,模糊规则数较大时MSE 值达不到最优,此时易发生过拟合的现象;模糊规则数较小时MSE值也达不到最优.因此,稀疏因子β起到了平衡系统性能和复杂度的作用,对β在使用交叉验证的方法寻优是必要的.

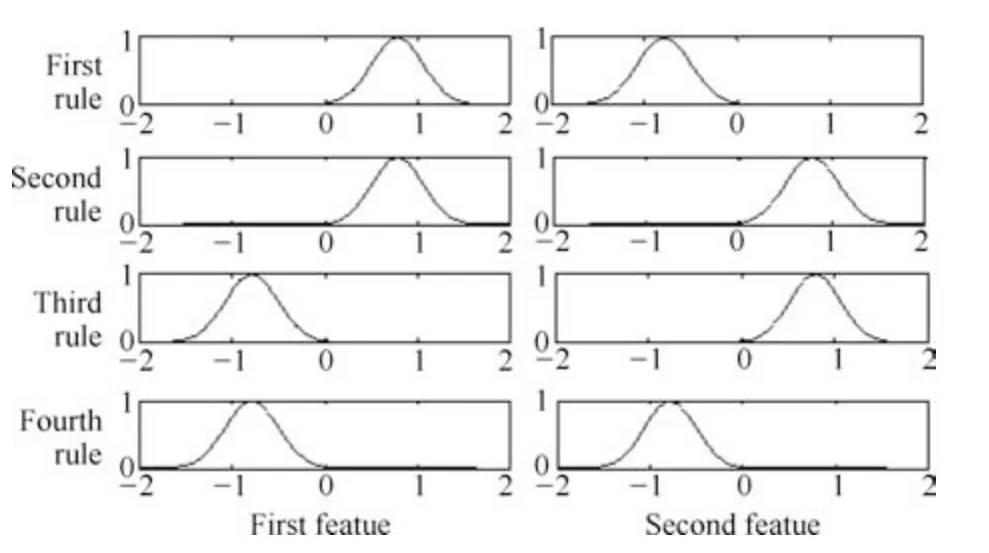
图3 PTSK在mexihat数据集上得到的模糊集示意图Fig.3 Fuzzy sets obtained by PTSK on mexihat dataset

为了考察PTSK模糊系统的收敛情况,图4给出了PTSK在mexihat,elevators,bodyfat和wizmir 数据集上某次运行的收敛曲线(固定参数β=4).从图中曲线可以看出,PTSK在这4个数据集上的迭代次数均小于200.此时模糊规则数和求得的规则前件/后件参数趋于最优值,系统的性能达到稳定.

3.3.2 非参数检验

本小节使用非参数检验中的Friedman 检验和Holm post-hoc检验来分析8种算法在28个数据集上MSE 值的统计学显著性差异,设置显著性水平α=0.05.Friedman检验是一种利用秩实现对多个总体分布是否存在显著差异的非参数检验方法.图5显示了8种算法在Friedman检验上Friedman秩结果.实验结果表明本文提出的PTSK模糊系统在25个数据集上取得了最佳结果.

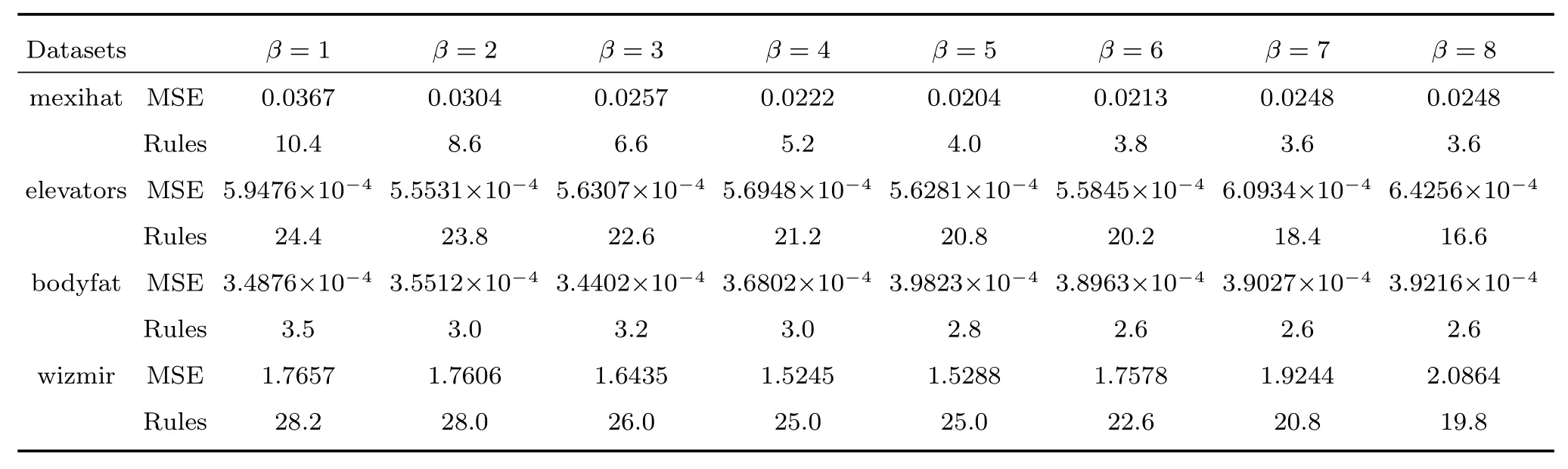
表7 mexihat,elevators,bodyfat和wizmir数据集上β 参数敏感性实验Table 7 Sensitivity experiments of parameterβ on mexihat,elevators,bodyfat and wizmir datasets

图4 PTSK某次运行的收敛曲线Fig.4 Convergence curves of PTSK at a certain simulation

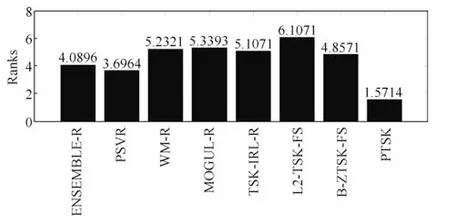
图5 8种算法的Friedman检验结果Fig.5 Friedman results of eight algorithms

Holm post-hoc检验作为事后分析方法,常用于根据Friedman检验结果进行最优算法与其他算法的两两比较分析.实验中将PTSK与另外7 种算法进行两两比较,如果得到的APV (Adjustedp-value)值小于显著性水平,即p <α/i,则说明PTSK模糊系统有显著优势,反之则说明两个算法的性能间没有显著差异.Holm post-hoc检验的结果如表8所示.从表8中数据可知,与对比的7 种算法相比,所提PTSK模糊系统在系统性能上具有显著优势.

表8 Holm post-hoc检验结果Table 8 Holm post-hoc results

4 结论

本文使用概率模型构建了一种新的概率TSK模糊系统PTSK.在模糊和概率理论的协同工作模式下,PTSK建立了结构辨识和参数优化的协同学习机制.该学习机制将TSK模糊系统的构建视为一个整体,能充分挖掘输入空间和输出空间之间的内在联系.PTSK基于最大后验概率估计,使用粒子滤波同时求得模糊规则数和前后件参数的最优解,解决了传统聚类法TSK模糊系统分阶段求解参数和模糊规则数需预先设定的问题.实验结果表明PTSK的逼近性能和模糊规则数均取得了令人满意的结果.应当指出,本文算法仍存在一些不足之处,例如,在大规模样本的回归问题中,PTSK的时间效率还有待提高;另外,PTSK能否有效处理带噪声的回归数据亦没有进行探讨,这将作为我们近期的研究重点.