基于趣味玩具的结构力学形象化教学法研究

王艺霖，李秀领，张玉明

(山东建筑大学 土木工程学院，山东 济南 250101)

结构力学作为土木工程专业的重要基础课，具有概念公式多、理论复杂、思维抽象等特点，学生普遍反映“难学”，教师也感觉“难教”。为了激发学生的学习兴趣和学习自信、改变课堂教学枯燥乏味的模式，相关教师一直在探索新的教学模式，取得了很多成果，其中很值得关注的是形象化教学法的引入与扩展应用。例如，孙敬敬[1]提出形象化教学改革应从三方面着手：将基本概念和知识点形象化，采用形象化案例式教学模式，借助计算机仿真软件将力学模型直观化、瞬态运动过程化；张亚琴等[2]使用形象直观的授课方法和课堂教学结构把握课程内容之间的联系，同时辅以多媒体教学手段；潘旦光等[3]探讨了用实验手段展现结构力学抽象理论的教学方法，增加3个层次的实验教学环节：课堂演示实验、理解性实验、探索性实验，培养学生主动学习的习惯；王琳鸽等[4]在一些重要内容的课堂讲解中引用了“吹气法”“沿力走”等具体的方法实例。

为了更切实地将知识形象化，还可制作实体教具。例如，夏雨等[5]研发了结构力学演示教学仪器；李修干等[6]设计了一种实验装置来演示静定结构和超静定结构不同的力学性质，并探讨了利用该装置开展实验的方法。王山山等[7]也研制了课堂教具，可直观地将静定结构和超静定结构的内力特性进行比较和检测。

形象化教学的本质是让学生有参与感、介入感。贾红英等[8]提出的“感而遂通”的概念，从本质上表达出了这一思想。基于此，自然可将形象化的思想延伸到趣味化[9]。趣味化的教学可更好地激发学生的学习兴趣和探索精神，达到“深入人心”的效果。

为了切实实践“趣味化”教学，本文提出在结构力学课程的教学中引入目前流行的聪明棒、磁力片两种趣味玩具，探讨它们在几何组成分析这部分教学中的具体应用方式，力求让力学知识生动活泼起来，达到让学生眼前一亮、耳目一新的教学效果，并可直接用于辅助解题。

1 基本概念演示探究

几何组成分析包含很多重要的概念，这些概念反复出现却又不易理解。为此，首先探讨采用聪明棒和磁力片来演示部分重要的基本概念。

1.1 铰接

(1)单铰：连接两个刚片的铰结点。

聪明棒和磁力片都可演示出单铰(图1、图2)。

图1 用聪明棒演示单铰

图2 用磁力片演示单铰

(2)复铰：连接两个以上刚片的铰结点。

聪明棒和磁力片也都可演示出复铰(图3、图4)。

图3 用聪明棒演示复铰

基于图3的实体教具，也可展示出自由度的数目(共5个)：整体的平动、转动，对应3个自由度；此外还有三个聪明棒之间的相互转动，对应2个自由度。

图4 用磁力片演示复铰

基于图4的实体教具，也可形象地解释复铰提供的约束数：本身3个刚片各有3个自由度，共9个，现在只剩5个，说明约束数为4个。

1.2 单刚结点

磁力片的角点即是单刚结点的实例(图5)。结点两边的杆件既不能发生相对平动，也不能相对转动。

图5 用磁力片演示单刚结点

1.3 瞬变体系

瞬变体系指的是在微小荷载作用下发生瞬间的、微小的刚体几何变形，然后成为几何不变体系。图6、图7分别是用聪明棒演示的两种瞬变体系实例。

图6 用聪明棒演示的瞬变体系示意1

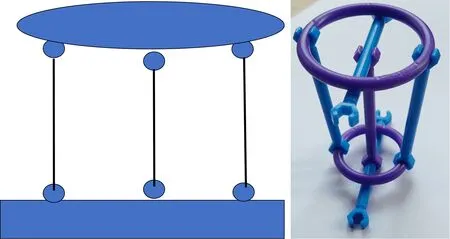
图7 用聪明棒演示的瞬变体系示意2

图6中的两个水平聪明棒只能发生瞬间的、微小的竖向变形，图7中的三个竖直聪明棒只能发生瞬间的、微小的水平向变形。

1.4 虚铰

虚铰是由不直接相连的两根链杆构成的。这两根链杆的杆轴可以平行、交叉，或延长线交于一点。

两根链杆的杆轴为平行的虚铰和两根链杆的杆轴延长线交于一点的虚铰，均可用聪明棒演示(图8、图9)。

图8 两根链杆的杆轴平行的虚铰

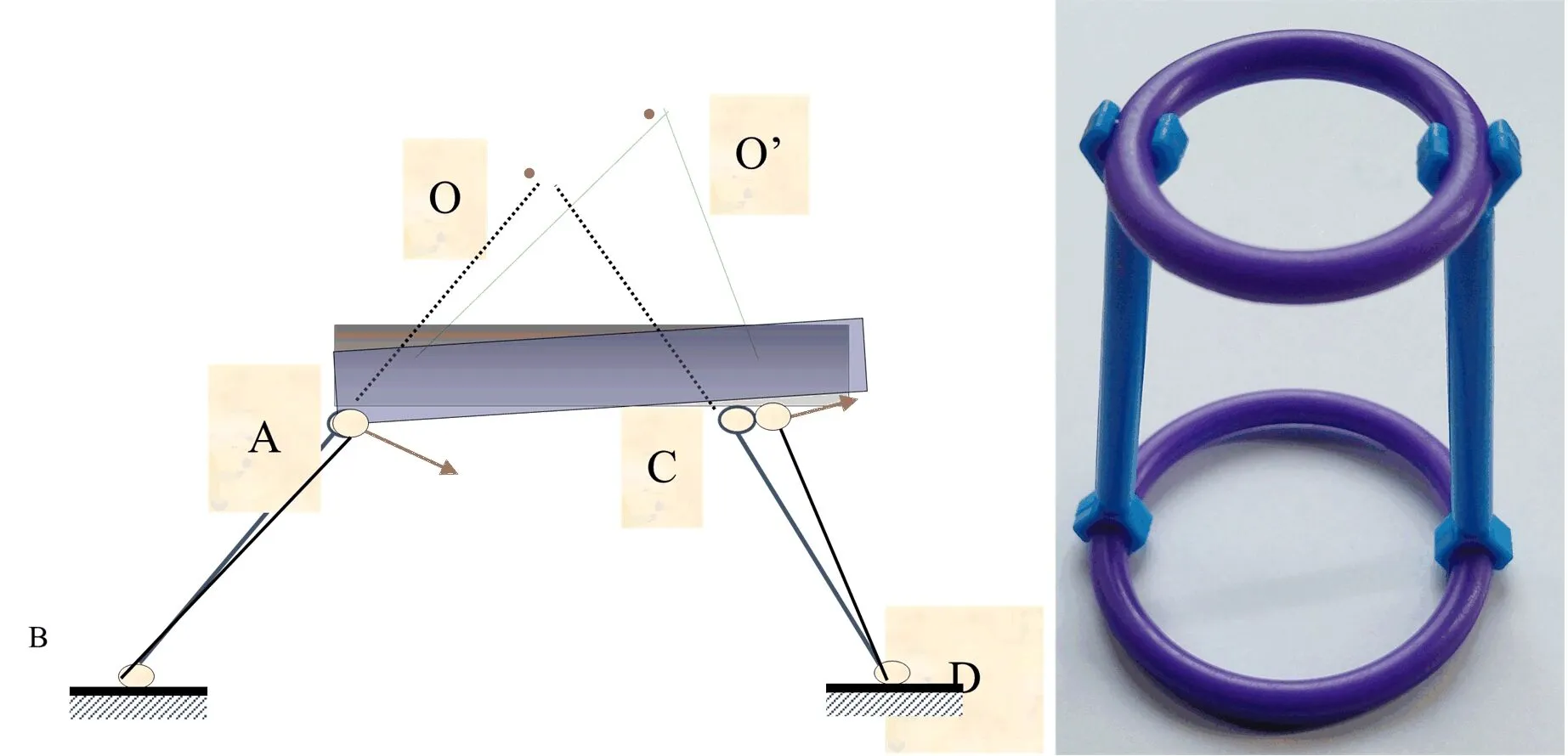
图9 聪明棒演示两个刚片由虚铰相连的情况

在图9中，两个刚片可以绕该交点(瞬时中心，简称瞬心)作相对转动。

当三个刚片由三个虚铰(三点交在无穷远的一条直线上)相连时，体系为几何可变体系，可以用聪明棒演示(图10)。

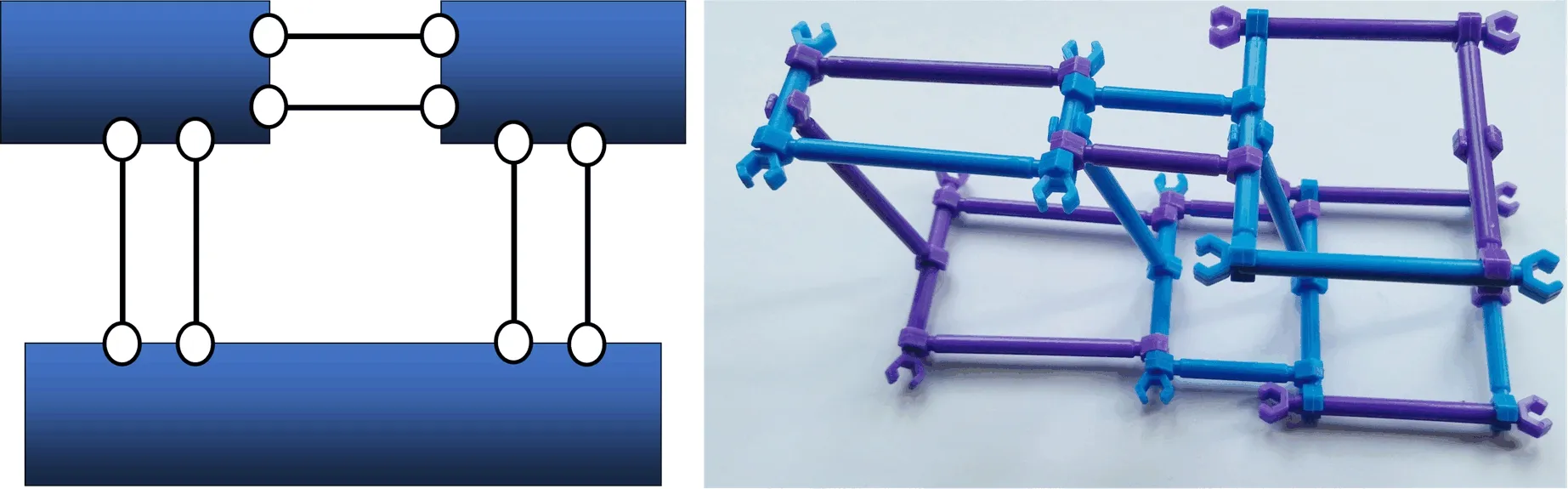
图10 聪明棒演示三个刚片由三个虚铰相连的情况

1.5 结点单杆

结点单杆分为两种情况：

(1)结点只包含两个未知力杆，且此二杆不共线，则每杆都是单杆，可用聪明棒演示(图11)。

图11 用聪明棒演示的结点单杆1

(2)结点只包含三个未知力杆，其中有两杆共线，则第三杆是单杆，可用聪明棒演示(图12)。

图12 用聪明棒演示的结点单杆2

2 几何不变体系的组成规律演示探究

2.1 一个点与一个刚片之间的组成方式

用两根链杆相连，且三铰不在一直线上，则可组成无多余约束的几何不变体系，可用聪明棒演示(图13)。

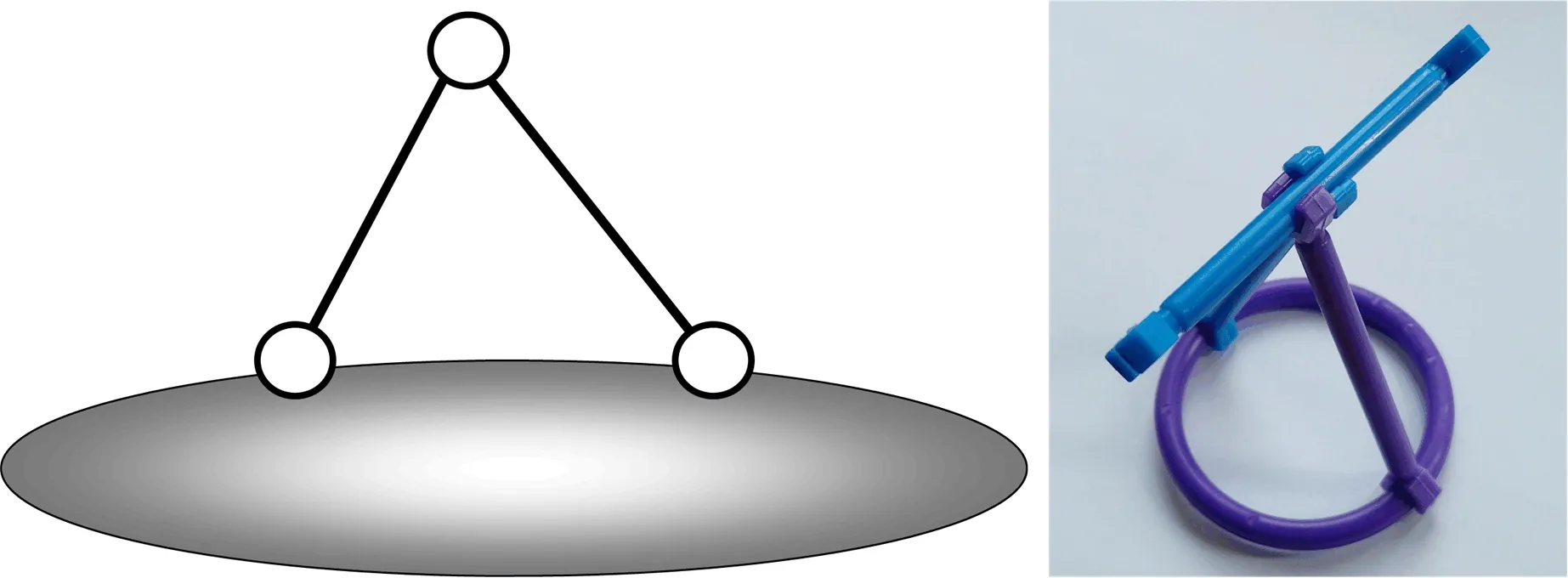
图13 用聪明棒演示的一个点与一个刚片的连接

2.2 三个刚片之间的组成方式

三个刚片用三个铰两两相连，且三个铰不在一条直线上，则可组成无多余约束的几何不变体系，可用聪明棒演示(图14)。

图14 用聪明棒演示的三个刚片的连接

2.3 三角形稳定性

组成几何不变体系的基本规律只是相互之间变相，本质上可以终归为三角形稳定性，可用聪明棒演示(图15)。

图15 三角形稳定性的演示

2.4 二元体特性

所谓二元体特性，指的是在体系上加上或拆去一个二元体，不改变体系原有的组成性质。图13中的两个斜杆即组成了一个二元体。

3 用聪明棒辅助解题

对于常见的一些几何组成分析题目，可根据题目上的图形，用聪明棒对应模拟出来，然后通过手动扰动来观察体系的位移和约束情况，达到辅助解题的效果。

例1某几何组成分析题目如图16所示。可用聪明棒模拟如图17所示。

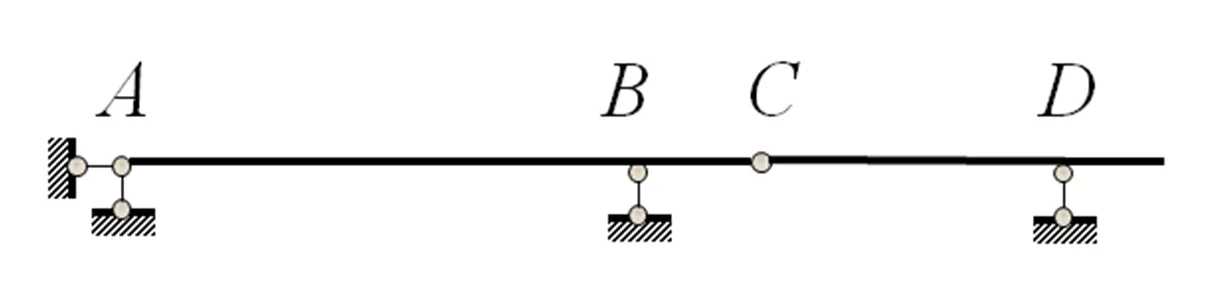
图16 几何组成分析题 例1

图17 用聪明棒模拟 例1

通过动手操作，观察体系位移和约束情况，可以发现该体系是没有多余约束的几何不变体系，从而达到了辅助解题的效果。

例2某几何组成分析题目如图18所示。可用聪明棒模拟如图19所示。

图18 几何组成分析题 例2

图19 用聪明棒模拟 例2

基于图19，通过动手操作，也可以发现该体系是没有多余约束的几何不变体系。

例3某两个几何组成分析题目如图20所示：

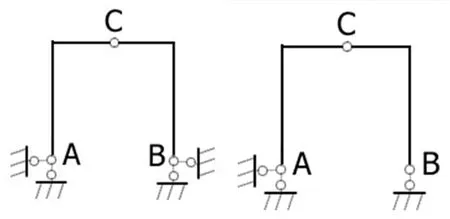
图20 几何组成分析题 例3

这两个题目比较类似，都可通过图21所示的聪明棒模拟体系来辅助分析：

注：图中的两个倒三角表示需要辅助施加的刚性约束，例如用手捏住以防此处出现相对转动图21 用聪明棒模拟 例3

捏住角部然后转动，观察支座处的位移分量。可得到结论：例3(a)，整体是没有多余约束的几何不变体系；例3(b)，整体是几何可变体系。

例4某几何组成分析题目及其聪明棒模拟如图22所示。

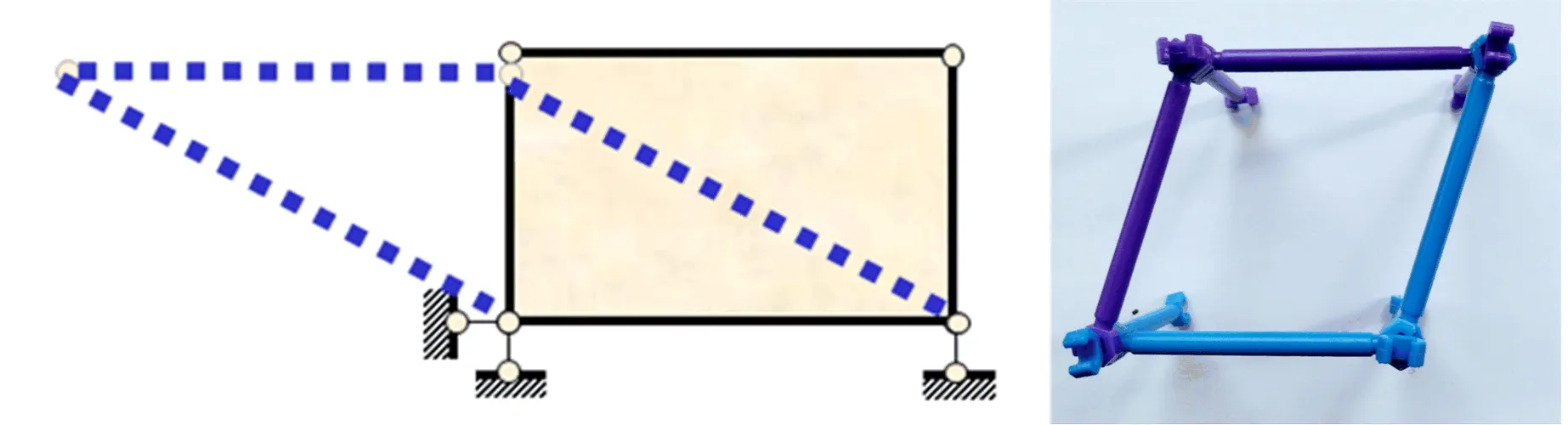
图22 几何组成分析题例4 及其聪明棒模拟

对其进行扰动操作，可以发现该体系为具有一个自由度的几何可变体系。

例5某几何组成分析题目及其聪明棒模拟如图23所示。

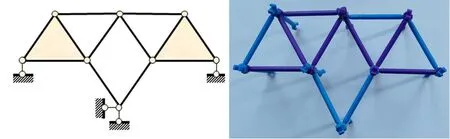
图23 几何组成分析题例5 及其聪明棒模拟

对其进行扰动操作，可以发现该体系为无多余约束的几何不变体系。

4 结语

根据结构力学课程中几何组成分析部分的内容特点，在教学实践中引入了趣味玩具——聪明棒和磁力片。基于对课程知识的深入理解，结合发散性思维，精心设计确定了应用方式，既能演示重要概念和规律，也能直接用于辅助解题。

这种特色鲜明的形象化教学法，可将结构力学中的抽象理论实物化，使教学的内容和形式更加丰富多彩。而且聪明棒和磁力片都价格低廉，适合大规模推广。在课堂上可将学生分成3～4人的小组，每一组分配一套教具，使学生可在有限的时间里获得动手操作的机会。

实践证明，这种简便有效地演示和操作能激发学生的学习兴趣，切实提升学生对知识点的掌握程度，提高其解题的准确性和自信心，同时还可以培养学生的发散性思维和创新能力。