矩阵的初等相似变换与初等合同变换

安 军

(重庆工商大学 数学与统计学院，重庆 400067)

矩阵的初等变换有三种类型：交换某两行或两列；将某一行或列乘以一个非零的数；将某一行或列乘以一个数加到另一行或列上去。两个m×n矩阵A,B等价是指矩阵A可以通过若干次初等变换化成矩阵B，或者说存在m阶可逆矩阵P和n阶可逆矩阵Q，使得PAQ=B；两个n阶矩阵A,B相似是指存在n阶可逆矩阵P(称为相似变换矩阵)，使得P-1AP=B；两个n阶实对称矩阵A,B合同是指存在n阶可逆矩阵P(称为合同变换矩阵)，使得PTAP=B[1]。矩阵的等价、相似、合同是矩阵理论中重要的三种等价关系，它们分别具有反身性、对称性及传递性，都可以用于研究矩阵的分类。因此，矩阵的等价标准形、相似标准形及合同标准形是矩阵理论的重要内容之一。

将n阶单位矩阵I经过一次初等变换分别得到n阶矩阵E(i,j),E(i(k))(k≠0)和E(i,j(k))，统称为n阶初等矩阵，其中特别注意：

任一n阶可逆矩阵都可以分解成若干个初等矩阵的乘积，初等矩阵都是可逆矩阵，它们有如下性质[1]：

E(i,j)T=E(i,j)，E(i(k))T=E(i(k))，

E(i,j(k))T=E(j,i(k))；E(i,j)-1=E(i,j)，

E(i(k))-1=E(i(k-1))(k≠0)，

E(i,j(k))-1=E(i,j(-k))。

两个n阶矩阵相似的充分必要条件是它们有相同的不变因子或相同的初等因子；两个n阶实对称矩阵合同的充分必要条件是它们的特征值中正、负和零的个数分别相同。

针对两个方阵相似以及两个实对称矩阵合同，本文分别介绍了初等相似变换与初等合同变换的概念，得到求相似变换矩阵及合同变换矩阵的一般方法，并以近年考研试题为例介绍这两种方法的应用。

1 初等相似变换

(1)交换A的第i,j两列，同时交换第i,j两行，即E(i,j)AE(i,j)；

(2)将A的第i列乘以非零数k，同时将A的第i行乘以1/k，即E(i(k-1))AE(i(k))；

(3)将A的第i列乘以数k加到第j列上，同时将第j行乘以数-k加到第i行上，即E(i,j(-k))AE(i,j(k))。

由于矩阵乘法具有结合律，故初等相似变换与先做初等行变换或先做初等列变换的顺序无关。

如果两个n阶矩阵A,B相似，即P-1AP=B。将可逆矩阵P分解成若干个初等矩阵的乘积P=P1P2…Ps，其中每个Pi都是某种类型的n阶初等矩阵，因而

由此可知，两个n阶矩阵相似的充分必要条件是其中一个矩阵可以经过若干次初等相似变换得到另一个矩阵。

例1(2019年全国考研数学一、二、三试题)：

已知矩阵

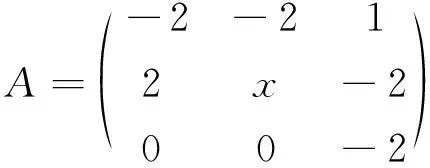
相似，(1)求x,y；(2)求可逆矩阵P，使得P-1AP=B。

解(1)因为相似矩阵有相同的迹和相同的特征值，因此

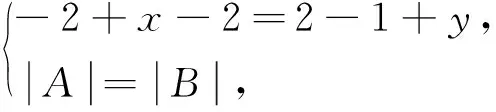
又|A|=-2(4-2x)，|B|=-2y，所以x=3,y=-2。

(2)

因此，所求的

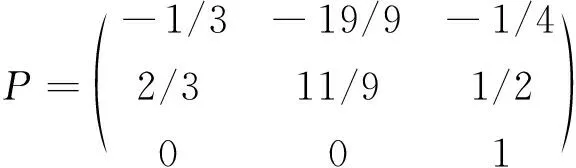
满足P-1AP=B。

注2由于将可逆矩阵分解成若干个初等矩阵之乘积不是唯一的，所以此类问题的答案往往不唯一。比如，文献[2]和[3]得到的相似变换矩阵P分别是

它们也满足P-1AP=B的题设要求。将这两个矩阵分别记为P1和P2，并将其与例1所得P的关系记为P=P1X1和P=P2X2。容易求得：

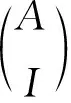
的约当标准形是

其相似变换矩阵P和其逆矩阵P-1分别是

2 初等合同变换

(1)交换A的第i,j两列，同时交换第i,j两行，即E(i,j)AE(i,j)；

(2)将A的第i列乘以非零数k，同时将A的第i行乘以k，即E(i(k))AE(i(k))；

(3)将A的第i列乘以数k加到第j列上，同时将第j行乘以数k加到第i行上，即E(j,i(k))AE(i,j(k))。

类似地，初等合同变换与先做初等行变换或先做初等列变换的顺序亦无关系。

如果两个n阶实对称矩阵A,B合同，即PTAP=B。将可逆矩阵P分解成若干个初等矩阵的乘积P=P1P2…Ps，其中每个Pi都是某种类型的n阶初等矩阵，因而

由此可知，两个n阶实对称矩阵合同的充分必要条件是其中一个矩阵可以经过若干次初等合同变换得到另一个矩阵。

例2(2020年全国考研数学二试题)：

设二次型

2ax1x2+2ax1x3+2ax2x3

解(1)二次型f和g的矩阵分别是

由题意知R(A)=R(B)，而|B|=0，故R(A)=R(B)<3，有|A|=(2a+1)(a-1)2=0，知a=-1/2。当a=1时，R(A)=1,R(B)=2，不合题意，故a=-1/2。

(2)

因此，所求的可逆矩阵

满足PTAP=B。

注1用第三种初等合同变换有时要用待定系数法计算k值。

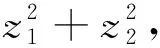
PTE(2,3)AE(2,3)P。

显然E(2,3)AE(2,3)=A，因此，这两个答案都符合题目要求。

3 结语

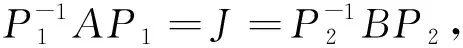
讨论两个n阶矩阵合同一般是限定在实数域上的对称矩阵，即讨论n阶实对称矩阵合同。由于初等合同变换比初等相似变换在计算上更容易些，所以有些高等代数教材中会有所介绍[1,5]。不过，教材中通常只讲如何将一个实对称矩阵经过若干次初等合同变换化成一个对角矩阵，几乎不涉及利用初等合同变换法解决如例2这种题型。