邻域信息约束融合Student's t 混合模型的医学图像分割
2021-04-17王燕贞陈志翔罗俊星
王燕贞,陈志翔,罗俊星
1. 漳州职业技术学院,福建 漳州363000;
2. 闽南师范大学,福建 漳州363000
图像分割是计算机视觉和图像处理的基础,其精准率直接影响图像理解、图像识别等后续工作.然而噪声的存在给图像分割带来了影响,特别是医学影像.以核磁共振图像为例,噪声和灰度不均同时存在,这使得医学图像的分割成为一大难点,而如何提高医学图像的分割精度也成为研究热点.
图像分割方法可分为两类:基于结构和基于概率统计.基于结构的方法又可分为基于区域和基于边缘两类.基于区域分割的Chan-Vese 模型适用于灰度均匀的图像,对于灰度不均的图像,比如医学图像在分割过程中会出现过分割现象.基于边缘分割的GAC 模型虽可以分割灰度不均匀的图像,但存在收敛速度慢和噪声敏感问题.文献[1]综合两种模型的特点,提出基于变动权值的混合水平集模型.该模型的能量泛函由局部能量项、全局能量项和长度约束项三部分组成,使用窄带法进行函数演化得到较简单的轮廓曲线逼近复杂图像.在不丢失细节的同时兼顾收敛速度,但模型的分割效果取决于权重参数的选择.文献[2]使用小波变换与中值滤波对脑MR图像进行噪声预处理后,通过在水平集方法中添加自适应加速因子提高分割速度.近年来,基于统计的聚类方法也广泛应用于图像分割.K-means(K 均值)和FCM(模糊C 均值)是最小平方误差聚类应用于图像分割的典型算法.宗晓萍等[3]使用K-means 算法对含有肿瘤的脑MR 图进行分割.通过对图像的不同灰度值进行聚类来提取肿瘤图像.传统FCM 随机生成聚类中心,存在聚类中心和噪声敏感问题.为了解决聚类中心初始值选择问题,文献[4]提出FCM_GSA 算法,引入改进的万有引力搜索算法,计算粒子所受的空间合力,将更新后的粒子位置作为聚类中心重新计算欧氏距离.该算法克服了FCM 算法聚类中心敏感问题,对复杂图像分割效果优于传统FCM.文献[5]将噪声图像进行小波变换,然后使用EM 算法预估小波系数;将FCM 聚类和变分方法结合,对水平集函数进行能量泛化,通过FCM 聚类获取聚类中心信息,完成图像分割.该模型能有效解决FCM 模型聚类中心、噪声敏感问题.文献[6]在FCM 的基础上,采用粒子群优化算法结合局部空间约束实现预分类,再采用阙值法纠正错分像素从而实现最终图像分割.该模型依赖于预分类的正确性,模型鲁棒性有待提高.FLICM 算法[7]为了权衡噪声和细节,引入模糊因子作为局部相似性度量.但由于模糊因子未能准确估计邻域像素的约束,使得该算法对高噪声的图像分割效果不佳.为了弥补FLICM 算法的不足,文献[8]提出NLFCM 算法,综合考虑图像中所有像素的非局部信息,从而提高了算法对高噪声图像分割的鲁棒性.
混合模型作为概率统计建模工具,能够对各种随机现象进行建模.目前,高斯混合模型(GMM)[9,10]由于其简单易实现已广泛应用于医学图像分割.但GMM 对于噪声和异常值敏感,特别是对重尾噪声的抗噪效果不佳.针对上述问题,文献[11]提出一种基于非对称Student's t 混合模型的鲁棒模糊聚类算法,该算法通过将相异度函数设为非对称Student's t 分布和均值模板的负对数似然来获得较好的分割结果和抗噪性.文献[12]提出一种基于EM 算法的Student's t 混合模型的活动轮廓分割方法,在代价函数中引入Student's t 混合分布,得到基于概率统计的水平集函数.受文献[13,14]启发提出一种邻域信息约束融合Student's t 混合模型(NSMM),使用滤波平滑噪声,对图像像素使用Student's t 混合分布进行建模,并使用EM 算法求解.该方法引入了局部空间约束,并使用有重尾特点的Student's t 混合分布. 实验结果表明,NSMM 与传统的K-means、FCM 和GMM 相比,对高噪声图像鲁棒性更强.
1 算法原理
1.1 邻域信息约束
假设图像X=(x11,…,xmn),xmn表示处于m 行n 列的像素点.取邻域空间模板3 ×3,如图1 所示.
像素点xmn的邻域像素集合定义为Ω(mn)= (xm-1,n-1,xm-1,n,xm-1,n+1,xm,n-1,xm,n+1,xm+1,n-1,xm+1,n,xm+1,n+1).结合中值滤波器和均值滤波器,判断图像像素点是否为噪声点,如果为噪声点,对噪声点进行重构;如果为非噪声点,保留原有灰度值.具体算法流程图如下:
(1)输入邻域空间3 ×3 模板像素点;
(2)判断模板中心点xmn的值是否为模板中的极值,如果是,则xmn为噪声点,转入步骤(3),如果否,xmn为非噪声,保留原值;
(3)对Ω(m,n)进行中值滤波操作,对Ω(m,n)中的元素排序,获取位于中间位置的两个像素点x1和x2;
(4)对x1和x2取均值,得到y 替换xmn,完成对噪声点的重构.
使用K-means 聚类算法如式(1),结合邻域信息获取重构后图像像素点的类别概率信息. 设图像有k个聚类中心为μ1,μ2,…,μk,每个聚类的样本数量为N1,N2,…,Nk,使用平方误差作为目标函数.
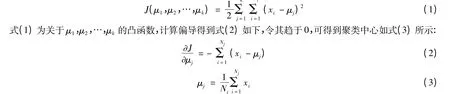

图1 像素点邻域空间信息Fig.1 Neighborhood spatial information of pixels
当迭代次数达到最大迭代次数或聚类中心变化小于阙值则停止迭代. 使用K-means 获得类型初始分类Imn,在初始分类基础上融合邻域信息约束,具体如式(4)和式(5)所示:

式(4)中,R 为邻域模板列所包含像素点个数,c 为邻域模板行所包含像素点个数,k 为类别,Δ(Imn,k)为像素点xmn与类别k 的相似度,若相同,取1,否则取0.Nm,n,k表示像素点xmn结合邻域类别信息获取的类别.β 为噪声平滑参数,Bm,n,k为像素点融合邻域信息后对类别k 的隶属度.
1.2 Student's t 混合模型和EM 算法
设图像X 由N 个像素点构成,X = (x1,x2,…,xN),使用Student's t 混合模型对图像进行建模,可知图像由K 个t 分布的加权来描述,具体如式(6)所示:

1.3 算法流程
(1)初始化邻域模板R、C,图像类别K,噪声平滑参数β,随机初始化参数集Θ 和Π,设置终止条件1 <L(Φ)t+1/L(Φ)t<1.001,t 为迭代次数.(2)E 步骤:根据式(13)和(14)计算ui、L(Φ).(3)M 步骤:更新参数集Θ 和Π.(4)判断是否满足终止条件,若模型收敛停止算法,根据最大后验准则获得像素分类;若不收敛,执行步骤(2).
2 实验与分析
实验样本取自BrainWeb 仿真医学影像数据库和IBSR 临床医学影像数据库.本研究方法邻域信息约束融合Student's t 混合模型NSMM 与K-means、FCM 和GMM 算法进行对比.实验中,取图像类别K = 4,噪声平滑参数β = 1,NSMM3 邻域空间模板取3 ×3,则R = C = 3;NSMM5 邻域空间模板取5 ×5,则R = C= 5;NSMM7 邻域空间模板取7 ×7,则R = C = 7.
2.1 评价指标
本文选取文献[15]中的DICE 作为分割效果优劣的评价指标.具体如式(15)所示:

其中Sseg表示待评价分割结果,Sgt表示标准分割. DICE 值越大代表重叠区域面积越大,分割准确率越高.本文样本为脑部磁共振(MR)图,正常脑组织划分为脑脊液(CSF)、灰质(GM)和白质(WM). 以DICE CSF、DICE GM 和DICE WM 分别代表脑脊液、灰质和白质的分割精度.
2.2 仿真脑部MR 图
图2 为7 %噪声条件下,本研究方法与其他三种不同方法分割第52 张、75 张、91 张和110 张仿真图的对比结果.图2 中的(a)为实验原图,(b)为标准分割结果,(c)~(f)分别为K-means、GMM、FCM 和NSMM3 的分割结果.表1 ~表4 为四种方法在7 %噪声下的DICE 指标对比.由图2 和表1 ~表4 可知,本文方法对CSF的分割效果与其他三种方法差别不大,但是对GM 和WM 的分割效果要明显优于K-means、GMM 和FCM.

图2 四张仿真脑部MR 图7 %噪声下的分割结果Fig.2 Segmentation results of four simulated brain MR images with 7 % noise

表1 第52 张仿真图7 %噪声下DICE 指标对比Tab.1 Comparison for DICE index on the 52th image with 7 % noise

表2 第75 张仿真图7 %噪声下DICE 指标对比Tab.2 Comparison for DICE index on the 75th image with 7 % noise

表3 第91 张仿真图7 %噪声下DICE 指标对比Tab.3 Comparison for DICE index on the 91th image with 7 % noise

表4 第110 张仿真图7 %噪声下DICE 指标对比Tab.4 Comparison for DICE index on the 110th image with 7 % noise

图3 四张仿真脑部MR 图9 %噪声下的分割结果Fig.3 Segmentation results of four simulated brain MR images with 9 % noise

表5 第52 张仿真图9 %噪声下DICE 指标对比Tab.5 Comparison for DICE index on the 52th image with 9 % noise

表6 第75 张仿真图9 %噪声下DICE 指标对比Tab.6 Comparison for DICE index on the 75th image with 9 % noise

表7 第91 张仿真图9 %噪声下DICE 指标对比Tab.7 Comparison for DICE index on the 91th image with 9 % noise

表8 第110 张仿真图9 %噪声下DICE 指标对比Tab.8 Comparison for DICE index on the 110th image with 9 % noise
2.3 临床脑MR 图

图4 四张临床脑部MR 图的分割结果Fig.4 Segmentation results of four clinical brain MR images

表9 第35 张临床脑MR 图DICE 指标对比Table 9 Comparison for DICE index on the 35th clinical MR

表10 第46 张临床脑MR 图DICE 指标对比Tab.10 Comparison for DICE index on the 46th clinical MR

表11 第60 张临床脑MR 图DICE 指标Tab.11 Comparison for DICE index on the 60th clinical MR
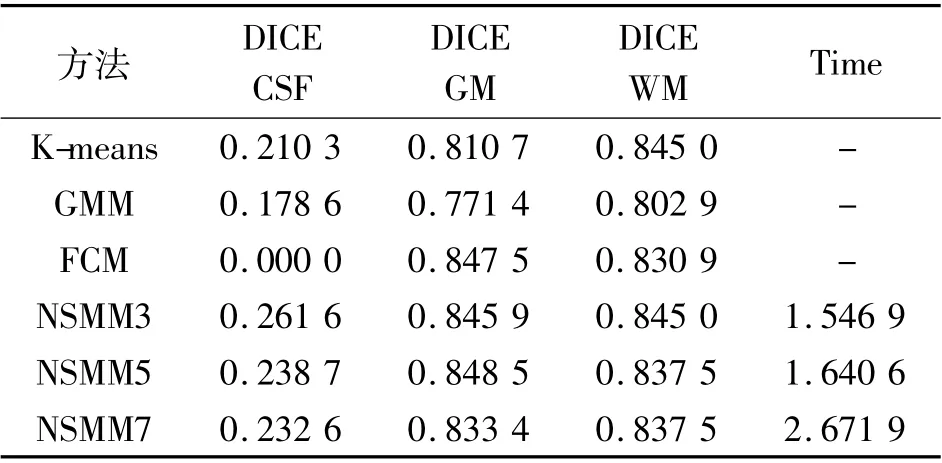
表12 第72 张临床脑MR 图DICE 指标Tab.12 Comparison for DICE index on the 72th clinical MR
图4 为本研究方法与其他三种不同方法分割IBSR05 数据集中第35 张、46 张、60 张和72 张临床脑MR 图的对比结果.图4 中的(a)为实验原图,(b)为标准分割结果,(c)~(f)分别为K-means、GMM、FCM和NSMM3 的分割结果.表5 ~表8 为使用四种方法进行分割的DICE 指标对比.真实临床脑MR 图,由于灰度不均匀,使用传统方法进行图像分割时,精度有待提高.由图4 和表9 ~表11 可知,本文方法由于考虑了邻域类别相关性,在第35、第46 和第60 张临床脑MR 图上,对于CSF、GM 和WM 的分割结果和分割精度上均优于K-means、GMM 和FCM.表12 中本文方法的DICE GM 和DICE WM 指标和FCM 算法接近,但FCM 算法分割不出CSF,而本文方法与其他方法相比仍能保持稳定的分割精度.由此可见,总体来说本文方法在DICE 指标上优于K-means 算法、FCM 算法和GMM 算法. NSMM3、NSMM5 和NSMM7 由于选取的邻域模板不同,在DICE CSF 的分割精度上也有不同表现.NSMM5 选取了像素点周边24 个像素作为邻域范围,NSMM7 选取了像素点周边48 个像素作为邻域范围,比NSMM3 扩大了邻域范围,不仅加大了计算成本,还降低了DICE CSF.可见邻域模板范围不宜过大,否则反而会降低分割精度,增加运行时间.由此可知,基于本实验样本的脑MR 图,邻域模板取3 ×3 可以获取较高分割精度.
3 结论
本研究提出一种新的邻域信息约束融合Student's t 混合模型的分割算法.该模型在使用滤波去噪声的基础上,通过噪声平滑因子获取像素类别隶属度从而实现邻域信息约束,并将其作为Student's t 混合模型中t 分布的权重,提高了传统SMM 用于图像分割时对高噪声的鲁棒性. 实验表明,本研究方法与Kmeans、GMM 和FCM 方法相比,均取得了较好的分割结果.本研究方法取不同邻域模板进行空间约束时,综合精确率和运行时间考虑,以33 模板最佳.但本研究方法的不足之处在于模型参数初始值随机生成,导致模型不够健壮,因此确定模型初始参数,提高模型的健壮性是下一步的研究方向.
