基于双匹配配准算法的多重复纹理图像拼接

张琳娜，陈建强，吴 妍，张 悦，岑翼刚

（1.贵州大学机械工程学院，贵阳550025；2.贵阳市公安司法鉴定中心，贵阳550025；3.北京交通大学信息科学研究所，北京100044）

引 言

图像拼接技术广泛应用于全景图像拼接［1-2］、虚拟现实［3-4］、无人机遥感图像拼接［5-6］及多图像视频拼接［7-8］等领域。针对不同的应用领域和不同的具体问题，配准算法的结构和性能不尽相同［7］，但目的相同：在规定的变换空间内寻找一种最佳变换，确保待配准的两幅图像之间达到某种意义的匹配。一般的图像拼接流程包括：特征提取、特征匹配、单应矩阵和图像融合［9］。

为了更好地实现图像配准，很多学者都在努力提取更快、更突出的特征。图像特征提取是对整幅图像进行降维描述，使用低维的图像特征向量来描述整幅图像。从最早期的Moravec算法［10］到Harris算法［11］，再到尺度不变特征转换（Scale-invariant feature transform，SIFT）［12］、SURF［13］、FAST［14］、ORB［15］和BRISK［16］算法，以及改进算法PCA-SIFT、ICA-SIFT、P-ASURF、R-ASURF和Radon-SIFT等，特征提取算法层出不穷。为了满足人眼视觉感受，得到更自然的拼接图片，文献［17］利用不同图像间信息进行互补融合。为了解决由像素几何未对准及目标运动引起图像重合区域“鬼影”效应［18］，文献［19］寻找一条最佳镶嵌线，在重叠区域寻找两幅图像的差异最小值。还有一部分学者致力于解决整体映射扭曲失真的问题。文献［20-21］提出了一些局部映射模型，提高对齐的质量，如APAP（As-projective-as-possible）［21］模型，将图像划分为密集网格，每个网格都用一个单应性矩阵对齐，用网格优化的方法来解决图像拼接对齐问题。这些方法大部分都是关于特征提取、单应矩阵和图像融合方面，在特征匹配方面涉及很少。

然而现实生活中有很多重复纹理的场景，比如超市的货架、高楼上的窗户或地面的地砖等。对于重复场景的拼接，不管是对于构建无人超市［22］，还是对于增强现实（Augmented reality，AR）的真实场景保持精确“对准关系”都是一种挑战［23-24］。通过实验分析发现，当图像中的物体存在较多重复纹理特征的场景时，拼接效果不理想的最大原因并不是因为提到的特征点不对，而是其特征点的误匹配率非常高。也就是说，特征提取算法会对相同且重复的物体提取同样的特征点，但是无法区分哪一个特征点属于哪一个目标，从而导致很多错误的特征点匹配。

图像匹配是图像拼接很重要的一步，若是匹配点对是一对错误的匹配，则变换的单应矩阵形变会有误差，影响拼接结果，所以需要在建立初始的匹配后，设计特征匹配策略，消除误匹配。常用的特征匹配策略是提取特征之后进行最近邻匹配，消除大部分的错误点，然后再用RANSAC方法［25］进行过滤。传统方法若是筛选条件太严格，过滤掉的匹配点对过多，剩下的匹配点对过少，容易引起仿射变换形变过大。若是筛选条件太松，则保留的错误匹配点对多，图像配准位置不对。所以本文提出双匹配配准（Double-match image registration，DMIR）算法，结合了两张图像的匹配和单张图片的自匹配，不仅能删除一些错误匹配点对，还能将部分错误匹配点对修改为正确匹配点对，从而得到更多、更准、分布更均匀的正确匹配点对，实现更好的拼接效果。

1 相关算法

1.1 特征提取算法

目前主流的提取特征算法包括SIFT、SURF、FAST和ORB等。其中FAST算法速度最快，可以提取大量特征点，但是质量不高。ORB在FAST基础上得到的特征点质量较高，但是特征点数较少且不稳定。虽然SIFT和SURF在特征点提取上都很稳定，且SURF速度比SIFT快，但是SIFT在尺度和旋转变换的情况下要比SURF效果要好。此外，即使少数的几个物体也可以产生大量SIFT特征向量，更有利于重复纹理场景图像拼接。

1.1.1 特征点检测

SIFT特征［12］使用高斯差分函数来定位兴趣点，即

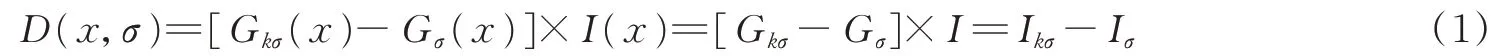
式中：Gσ(x)为高斯核函数；Iσ为使用Gσ(x)模糊的灰度图像；k为决定相差尺度的常数。兴趣点是在图像位置和尺度变化下D(x，σ)的最大值和最小值点。这些候选位置点通过滤波去除不稳定点。

1.1.2 特征描述子

以获取的特征点为中心，取其邻域16×16的像素点作为采样点，将采样点与特征点的相对方向通过高斯加权后归入包含8个bin的方向直方图［12］，最后获得4×4×8的128维的特征描述子。

SIFT描述子在每个像素点附近选取子区域网格，在每个子区域内计算图像梯度方向直方图［12］。每个子区域的直方图拼接起来组成描述子向量。SIFT描述子的标准设置使用4×4的子区域，每个子区域使用8个小区间的方向直方图，会产生共128（4×4×8=128）个小区间的直方图。

1.2 K-近邻算法

K近邻（K-nearest neighbor，KNN）算法［26］工作原理是对给定测试样本，计算距离度量找出训练集中与其最靠近的K个训练样本，然后基于这K个“邻居”的信息进行预测。假设一个特征点在特征空间中，其K个最相似的特征点的所属类别，即为该特征点的类别。设存在于N维欧式空间中的特征点。通过计算一个特征点与其他所有特征点之间的距离，根据距离远近进行加权平均，距离越近的样本权重越大。这里，对该特征点与所有特征点之间的距离进行排序，距离越近排名越靠前，当选取K个邻居时，只需取前K个特征点即可。此外，采用不同的距离计算方式，找出的“近邻”可能也会有差别。常用的计算相似度的距离包括欧氏距离、余弦距离和马氏距离。欧氏距离利用平方差来计算，可以较好地表现个体数值特征的差异。余弦距离能在方向上体现特征之间的差异。马氏距离表示数据的协方差距离，计算不稳定，会夸大变化微小的变量作用，且计算量大。由于特征点较多，所以本文采用欧氏距离计算特征点之间的距离。

2 双匹配配准算法

由于视角、光照、尺度和Gσ(x)噪声等因素，使得在相似性度量中距离最近的特征对并不能保证它们对应于与三维场景中的同一点，即存在误匹配。利用传统的方法对多重复纹理的图像进行拼接，效果并不理想。通过实验发现并不是是因为检测到的特征点不对，而是因为对于重复的物品，检测到了相同的特征点，匹配的位置有偏差。由于多重复纹理图像的公开数据集较少，本文采集了240张超市图像（包括左右拼接、上下拼接、多图拼接），共计可获拼接图像200张。以其中一张为例（图1），图像中相邻位置的物体是一样的，因此极易将图1（a）中红框内的物体与图1（b）中红框内物体进行错误匹配。对于相同物体匹配而言，并没有匹配错误，只是位置错了，使得拼接结果不理想。而图1（a，c）所示为正确的物体匹配。

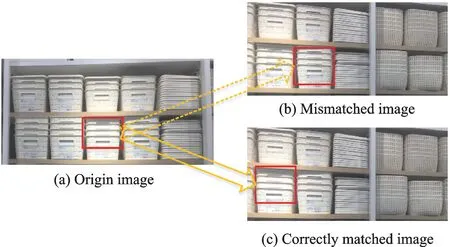
图1 超市图像匹配Fig.1 Supermarket image matching

为了得到相同物体的位置关系，考虑到自匹配特征点，可以获得相对位置信息。本文提出DMIR算法，即将图像之间的特征匹配与图像自匹配相结合。首先对图像间的特征进行匹配，得到初始匹配点对。然后进行自匹配得到相同特征点的相对位置信息，对初始的匹配点对进行筛选与修改，从而确保图像间匹配留下的正确匹配点对多且准确。

特征点配对采用KNN算法，由于特征点比较多，保留距离最近的和距离次近的特征点就可以得到足够的匹配点对，因此这里取K=2，具体过程如下：

步骤1待匹配图像提取SIFT特征点。

步骤2利用KNN算法进行图像间的匹配，得到初始匹配点对。图像间的匹配，即计算原图的一个特征点与待匹配图的所有特征点的欧式距离。当最小距离与次小距离的比值小于某个阈值时，说明最小距离对应的两幅图中的两个特征点很相似，匹配可靠性强，因此保留该匹配点对；否则删除该匹配点对。对两幅图匹配中所有保留下来的匹配点对距离进行升序排序，保留前400对，得到初始匹配点对。

步骤3利用KNN算法对原图进行自匹配，得到自匹配点对。自匹配即是计算原图中一个特征点与除了自身之外的所有特征点的欧式距离，保留距离最近的点，这样原图中的每一个特征点均可得到一个自匹配点对。将原图得到的所有自匹配点对距离进行升序排序，保留前400对，从而得到可靠的自匹配点对。

步骤4从初始匹配点对中进一步筛选出正确匹配点对。首先计算初始匹配点对中每个点对的匹配强度，得到种子点对。然后根据种子点对与自匹配点对、初始匹配点对的位置信息，确定更多正确的匹配点对。

该算法最大的优势是不仅能删除错误匹配点对，还能将一部分的错误匹配点对修改为正确的匹配点对，从而使得到的匹配点对分布更均匀，也更准确。为了实现该算法，需要解决以下两个问题：（1）如何计算种子点；（2）如何根据种子点将错误匹配点对修改为正确匹配点对，分别详细叙述如下。

2.1 种子点的确定

提取了SIFT特征之后，本文利用KNN进行了匹配，得到初始匹配点对(m1i，m2j)，其中m1i为第1幅图的特征点，m2j为第2幅图的特征点。如果在第1幅图中，设以m1i为中心、R为半径的邻域内包含了K个特征点n1k，k=1，…，K（不包括m1i），该集合记为，则这K个点在第2幅图中的匹配点为n2l，l=1，…，L，该集合记为。如果(m1i，m2j)为一个正确的匹配点对，那么其邻域内必然存在更多的匹配点对(n1k，n2l)。R根据图像大小设定，取图像的长（或宽）值的八分之一。因此可以计算点对(m1i，m2j)匹配强度［27］，公式为

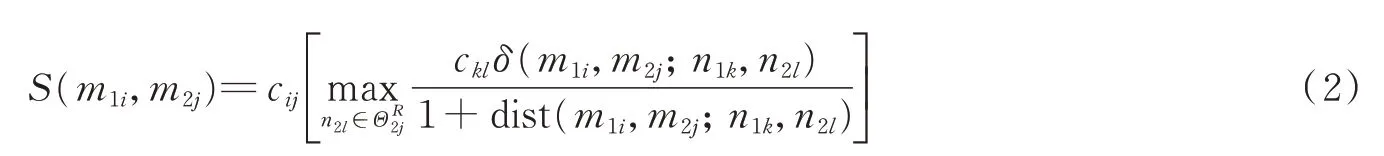
式中：cij，ckl为相关匹配值，本文都设为1；dist(m1i，m2j；n1k，n2l)为两对匹配点对欧式距离的均值，定义为

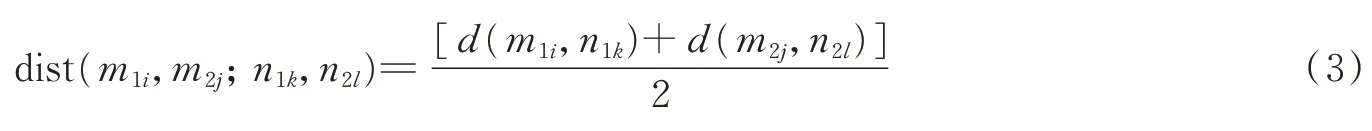
式中d(m1i，n1k)=|m1i-n1k|。δ(·)为指数函数，表达式为

式中：若ε接近于0，则约束d(m1i，n1k)和d(m2j，n2l)差异越小，选择的邻居点也较少，选出的种子点可靠度会降低，根据实验尝试，本文选取ε取0.3，γ定义为

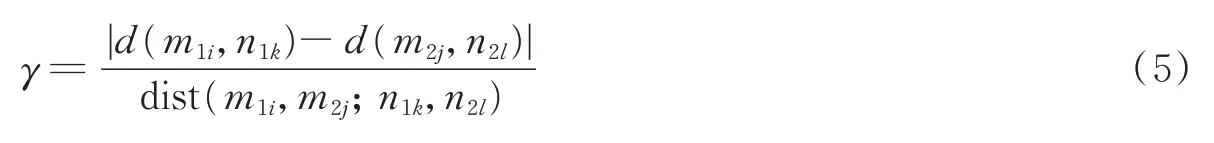
由于初始匹配点对会存在特征点一对多的情况，比如原图中的一个特征点会和匹配图的多个点得到不同匹配点对。而max操作可以保证原图上的匹配点从匹配图中只能找到距离最小的一个特征点进行匹配，避免一对多情况。同样地，匹配点对里，原图中也有可能存在多个特征点对应于匹配图一个特征点的情况。对于多对一的情况，通过计算γ确定候选匹配点对(n1k，n2l)对于(m1i，m2j)贡献度来解决，准确的点对贡献度高，错误的点对贡献度低。具体地，第1幅图中的(m1i，n1k)与第2幅图中的(m2j，n2l)距离越接近，那么γ→0，δ(·)越接近于1，(n1k，n2l)对于(m1i，m2j)贡献度也就越大；反之，第1幅图中(m1i，n1k)与第2幅图中(m2j，n2l)距离越远，δ(·)越接近于0，(n1k，n2l)对于(m1i，m2j)贡献就越小。

通过式（2），选取匹配强度S(m1i，m2j)大于1的点作为种子点S。种子点虽然是选出来的最为准确的点，但是由于少而且集中，仅利用种子点进行匹配形变可能会很大，拼接效果不好。

2.2 基于种子点的匹配点对确定

遍历所有的初始匹配点对，根据种子点对与自匹配点对、初始匹配点对的位置信息，确定最终正确的匹配点对。如图2所示，图（a～c）中左图为待拼接图，设点n1和m1为待拼接图中相同物体上的特征点，且它们是一个自匹配点对(n1，m1)，(s1，s2)为计算出来的种子点对，种子点对与自匹配点对有3种位置关系：种子点在自匹配点对的右边（图2（a）），种子点在自匹配点对的左边（图2（b）），种子点在自匹配点对的中间（图2（c））。

设图2（a，b）右图中一个初始匹配点为m2，其对应左图的初始匹配点为n1，此时则以ds2m2=|s2-m2|为参考，计算ds1n1=|s1-n1|以及ds1m1=|s1-m1|，若ds1n1与ds2m2更接近，则选择(n1，m2)为正确匹配点，否则选择(m1，m2)为正确匹配点。值得注意的是，这里图像的坐标轴是以左上角为原点，向右为x轴正坐标，向下为y轴正坐标。若左图种子点在自匹配对中间（图2（c）），则可直接根据特征点所在的x轴坐标位置判定，即根据右图种子点s2在匹配点m2的左边或右边，直接在左图中选择在s1左边或右边的点作为m2的正确匹配点，例如在图2（c）中，s2在m2的左边，因此选取m1为m2的正确匹配点。

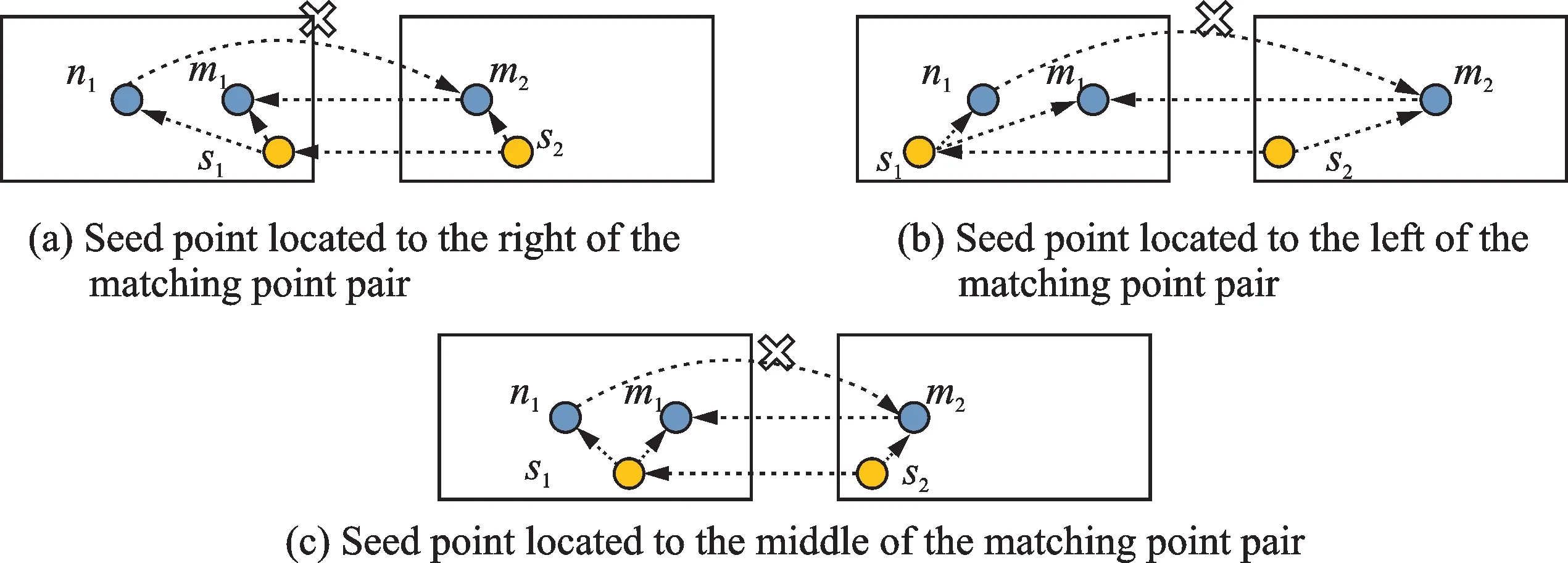
图2 种子点与匹配点对的位置关系示意图Fig.2 Position relationship between seed points and matching point pairs

3 实验结果及分析

3.1 实验过程

为了检验本文提出算法的有效性，实验在Visual Studio 2013上进行，用C++编写代码实现。DMIR算法图像匹配过程如图3所示。首先提取图像SIFT特征，然后通过KNN算法对同一张图的特征点进行自匹配和不同图像间特征点进行相互匹配，接着利用DMIR算法修改错误匹配点对，实现图像配准。最后利用所有点的常规方法计算多个二维点对之间的最优单映射变换矩阵（单应矩阵），将所有图片扭曲到一个平面上，进行图像融合，完成拼接。

图3 图像配准过程Fig.3 Image registration process

实验特征点匹配结果如图4所示，图中黄色较水平的线代表正确匹配点对匹配，紫色上下交错的线代表错误的匹配点对。图4（a）是提取SIFT特征点之后，两张图之间利用KNN得到的初始匹配点对，从图中比较明显地看到有很多是匹配错误点。图4（b）是左图与左图进行匹配得到的自匹配点对。货架上的商品是重复摆放的，所以自匹配之后，得到的是物体与自己相邻相同物体的匹配。图4（c）是利用RANSAC筛选后得到的匹配点对匹配，相对集中在一片区域中，对于整张图来说，分布并不均匀，也存在一些错误的匹配点对，如紫色线位置。图4（d）是本文提出的DMIR算法筛选后得到的匹配点对，从图中可以看出，从上到下匹配点对分布均匀，且准确率更高。

图4 图像匹配结果Fig.4 Image matching results

3.2 算法性能比较

本文在配准的过程中将RANSAC算法与本文算法的匹配点对结果进行比较。如图4所示，图像经KNN算法得到初始匹配点对是400对，自匹配点对400对，DMIR算法筛选后的特征点对是275对。其中初始匹配点对中，正确的匹配点对是249对，匹配准确率为62.3%。经DMIR算法筛选后准确率达到100%，且正确匹配点对由249对提升到275对，如表1所示，说明本文算法不仅可以有效地删除错误点对，还可以将一部分错误点对修改为正确的匹配点对。

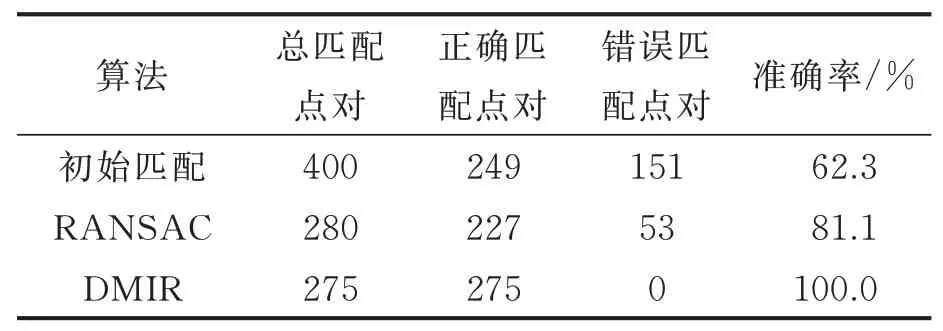
表1 匹配点对准确率Table 1 Accuracy of matching point pairs

RANSAC算法筛选后的（图4（c））的匹配点对是280对，正确匹配点对是227对，匹配准确率为81.1%。从图4可以看出，在筛选出来的匹配点对数目很接近的情况下，本文算法所得到的特征匹配点对更均匀，且更准确。此外，本文对采集的240张超市图像进行拼接（包括左右拼接、上下拼接和多图拼接），共计可获拼接图像200张。使用RANSAC算法进行匹配，得到的平均匹配准确率为70%，而本文算法平均匹配准确率可以达到88%。

本文也对匹配点对数量对拼接图像的影响进行了实验。实验从CVPR 2020 Google图像匹配［28］挑战赛测试集中选择2张图像进行特征点匹配并进行拼接。图5（a1）表示特征点匹配相似度距离要求宽松情况下使用RANSAC算法的匹配图，图5（a2）表示特征点匹配相似度距离要求严苛情况下使用RANSAC算法的匹配图，图5（a3）表示使用DMIR算法筛选过后的特征点匹配图，图5（b1～b3）为图5（a1～a3）对应的拼接结果。从图5中可以看出：在约束较松的情况下获得匹配点对比较多，但是错误的匹配点对也比较多，在进行图像拼接时，第2张图直接贴到了第1张图上，并没有达到图像拼接效果；在约束较紧的情况下得到的匹配点对比较少，也会出现仿射矩阵计算不准确的情况，达不到图像的拼接结果；而使用DMIR算法可以得到多而准确的匹配点对，实现了图像拼接。

图5 图像匹配点对数量对图像拼接质量的影响Fig.5 Influence of the number of image matching points on the quality of image stitching results

为了进一步比较算法性能，本文对消耗的时间进行了对比。根据3.1节的过程，本文对不同大小图像每个阶段的平均时间进行了统计，结果如表2所示。从表2可以看出：DMIR算法包括利用KNN算法进行自匹配和匹配筛选过程，其中自匹配时间消耗时间较长；图像越大，消耗的时间也会越多；对于尺寸较小图像，本文算法时间消耗小于RANSAC算法。

表2 算法时间比较Table 2 Comparison of algorithm time s

3.3 匹配结果对比

首先本文将DMIR算法的图像匹配结果与一些经典算法，如Hessian-SIFT、SURF、AKAZE［29］、ORB等算法，和一些最新的算法，如DOG+HardNet［30］、KeyNet+HardNet［31］、R2D2［32］、D2-Net（MS）［33］、Super Point（2k）［34］等算法的结果进行了对比。实验数据选自CVPR 2020 Google图像匹配挑战赛florence_cathedral测试集，如图6所示。参考文献［28］，图中高于5像素阈值的错误匹配项以红色绘制，低于5像素错误阈值的匹配项按其错误从0像素（绿色）到5像素（黄色）进行颜色画线，没有统计错误项的用蓝色绘制。从图6中可以看出：本文算法得出的匹配点对和DOG+HardNet算法一致，都是由表示0像素错误匹配点对的绿色线画出，即均为正确匹配点对，只是本文DMIR算法得到的匹配点对数量相对较少；但是DMIR算法特征点配对结果明显多于SURF和ORB等经典算法，且匹配正确率明显高于R2D2、D2-Net和SuperPoint等最新匹配算法。

图6 不同算法的特征点匹配结果对比图Fig.6 Comparison of feature points matching results of different algorithms

为了证明DMIR算法的有效性，本文对有重复纹理场景的图片进行拼接，并和其他算法结果进行了对比，如图7所示，其中红圈内表示的是一些细节差别。图7（a）是特征匹配后Ransac算法筛选后的拼接结果，图7（b）是适合相似结构匹配的块匹配算法拼接结果，图7（c）是本文DMIR算法的拼接结果。

第1行中，图7（a1）虽然拼接的商品没有错位，但是有货架未对齐，这是因为有错误的匹配点对太多，当计算单应矩阵时就会出现仿射偏差。图7（b1）中位置对齐了，但是形变很大，说明它是通过正确匹配点对计算的单应矩阵，但是正确匹配点对过于集中，不够均匀，引起仿射变换形变较大。图7（c1）说明了本文算法的有效性。

第2行中，图7（a2）同样存在位置未对齐问题，红圈内的柱子错位的拼接在一起。图7（b2）拼接位置有偏差，屋顶灯饰未对齐，且数量不对，红圈内本应是3个灯笼变成4个灯笼，拼接效果较差。图7（c2）表示本文算法结果无论是灯饰还是柱子，拼接对齐质量都很高。

第3行中，更多重复纹理商品的货架上更直接体现出本文算法的有效性。从图中很明显可以看出，原场景上方有3个排气扇，而图7（a3）和图7（b3）拼接图中只包含2个排气扇，位置误差较大。货架上的商品也存在较大的位置偏差。综合对比实验结果可以看出，本文方法形变更小，对于多重复纹理场景图片匹配更准确也更稳定。

此外，本文也对多张图拼接的图片进行了测试（图8），其中图8（a1～a4）分别为日出待拼接的左图、中间图、右图和拼接结果图；图8（b1～b5）分别为高楼待拼接的左上图、右上图、左下图、右下图和拼接结果图。可以看出，图8（b）包含了窗户和网格等重复纹理。并且对图像融合的边缘采用加权平均法进行优化，都获得了高质量的拼接图。

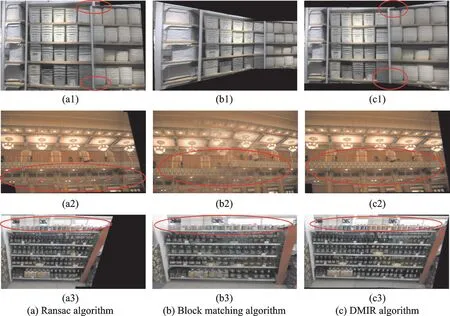
图7 不同匹配算法处理后的拼接图Fig.7 Image stitching results by different algorithms

图8 多张图像的拼接结果Fig.8 Stiching results of multiple images

4 结束语

图像拼接广泛应用于生活中，但是将此技术应用到无人超市检货、AR现实场景拼接中仍然存在拼接效果不好的问题。因为现实中存在多重复纹理的场景，对检测出来的特征点进行匹配，往往会匹配错位置。针对目前图像匹配算法对于重复纹理匹配准确率低的问题，提出图像内自匹配与图像间匹配相结合的方法，从而保留多而准确的特征匹配对，实现更好的图像拼接。对比实验和拼接结果证明了本文所提DMIR算法的有效性。但是对于有些图片匹配点对并不能完全准确，图像越大耗时越长，后续工作将进一步改进优化。