带有N策略,启动时间和服务台故障的M/M/1排队的均衡策略

蒋毓灵,刘力维

(南京理工大学理学院,江苏 南京210094)

1.引言

近年来,从经济学的角度对各种排队系统的策略行为进行研究已成为排队理论研究的一个新趋势.在经济学模型的排队系统中,顾客进入排队系统时,对于拥挤现象引起的等待,往往通过最大化自己的利益来决定自己的去留.但他们的行为往往会受到其他顾客的影响,也正是这种影响的存在,每个顾客的策略选择都可看作是与其他顾客之间的博弈.从博弈论的角度对排队系统中顾客行为的研究最早可追溯到1969年Naor[1]发表在《Econometrica》上的文章,他研究了简单线性收支结构下的可见M/M/1排队系统.Edelson和Hildebrand[2]考虑了相同的排队模型,但是是不可见情形,即到达的顾客在做出决策时无法获得有关队列状态的任何信息.此后,大量学者开始了对Naor,Edelson和Hildebrand的排队模型的扩展性研究,Economou和Kanta[3]讨论了在可见情况下,具有故障和修复的M/M/1队列的均衡策略.LI等人[4]研究了文[3]里的相同模型,但是是不可见情形.WANG和ZHANG[5]和YU等人[6]分别研究了在可见和不可见情况下,具有止步和延迟修复的M/M/1队列的均衡策略.

在现实生活中,机器的启动时间是不可忽略的.对于一些高能耗的服务,在人数很少时,我们不可能始终开着机器,否则从经济的角度来看,不利于利益的最大化,所以对关闭启动的研究是很有必要的.许多文章都有对启动时间的研究,部分可参考文[7-9].又由于昂贵的启动成本,许多服务系统会采取一些控制策略来打开或关闭服务设施.在这些策略中,N策略是最经常采用的.当系统变空时,服务台将切换到休眠状态,直到系统中的顾客数量达到给定的阈值N时,服务台才会被激活.带有N策略的开创性工作可以追溯到Yadin和Naor[10]的多个假期的M/M/1排队.GUO和Hassin[11]是第一个在具有N策略的单个马尔可夫队列中研究客户和社会优化的均衡进入策略的工作.另外,Burnetas和Economou[12],WANG等人[13]和ZHOU等人[14]也对N策略有所研究.

一些文章考虑了带有N策略和服务台故障的M/M/1排队模型.本文最大的创新是增加了启动状态,这使得模型和方程更加复杂.文章的其余部分安排如下:第2节是模型描述,第3节给出了服务台不同状态下的均衡到达率,第4节给出了均衡的社会收益函数,第5节对均衡到达率和均衡社会收益进行了数值研究.

2.模型描述

我们考虑一个带有N策略,启动时间和服务台故障的M/M/1排队系统.假设系统中顾客的到达服从参数为λ的泊松分布,服务规则是先到先服务(FCFS),服务时间服从参数为µ的指数分布.当服务台处于休眠状态时,它不为顾客提供任何服务,并且只有当系统中等待顾客人数达到给定的阈值N时,服务台才会开始启动,启动时间服从指数分布,参数为θ.系统服务台不是完全可靠的,在正常工作时有可能发生故障,假设顾客发现服务台故障时就不再进入系统,且服务台发生的故障是完全故障,即服务台停止服务并立即进行维修.服务台发生故障的过程是参数为ξ的泊松过程,维修时间服从参数为η的指数分布.当服务台处于正常工作状态时,它遵循空竭服务规则.当系统变为空时,服务台关闭,即服务台再次转为休眠状态.另外我们假设顾客的到达过程,服务台的服务过程,启动过程,故障过程和维修过程均相互独立.

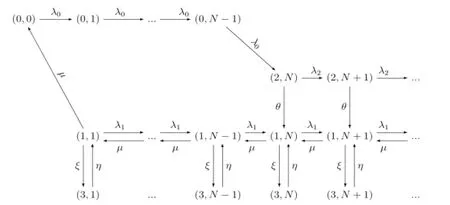
图1 模型的状态转移图

顾客在到达时需要决定是否进入系统,一旦进入就不能离开,直到服务完成.假设每个服务完的顾客能得到R单位收益,每逗留单位时间需要支付C单位费用,逗留时间包括等待时间和服务时间.所有的顾客都是理性的,他们希望能使自己的净收益最大化.更具体地说,当收益大于支出时,顾客进入系统;收益小于支出时,顾客止步;收益等于支出时,进入和止步均可.

我们用{I(t),N(t),t ≥0}表示时刻t时系统的状态,其中I(t)表示服务台的状态,N(t)表示系统中的顾客数,

显然,{I(t),N(t),t ≥0}是一个连续时间马尔可夫链,状态空间

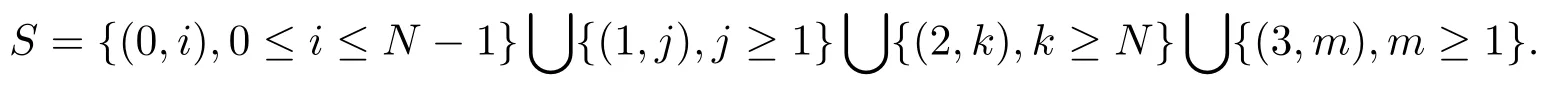
本文研究的是几乎不可见情形,即到达的顾客只能知道服务台的状态而不能知道系统中顾客数.实际上,顾客到达时的入队概率和服务台的状态有关,我们假设所有顾客的入队概率为qi(i=0,1,2,3),那么系统的有效到达率λi=λqi.又因假设顾客发现服务台故障时就不再进入系统,故q3=0,那么λ3=0.状态转移图如图1所示.

3.均衡到达率

在这一节,我们研究均衡到达率.首先令{p(0,i),0≤i ≤N −1;p(1,j),j ≥1;p(2,k),k ≥N;p(3,m),m ≥1}为马尔可夫链{I(t),N(t),t ≥0}的稳态分布,相应的部分生成函数如下:

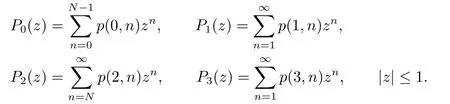
引理3.1在带有N策略,启动时间和服务台故障的M/M/1排队系统中,给定到达率(λ0,λ1,λ2),服务台在状态为0,1,2,3时的稳态概率分别如下:

其中,

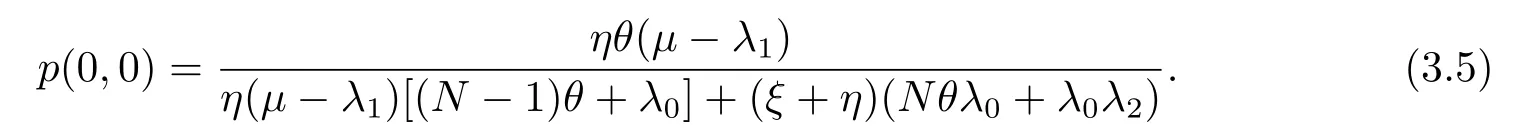
证稳态分布的平衡方程如下:

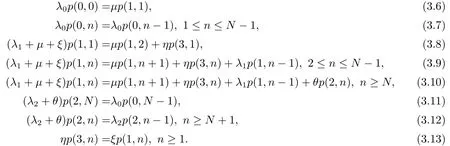
由(3.7)可得

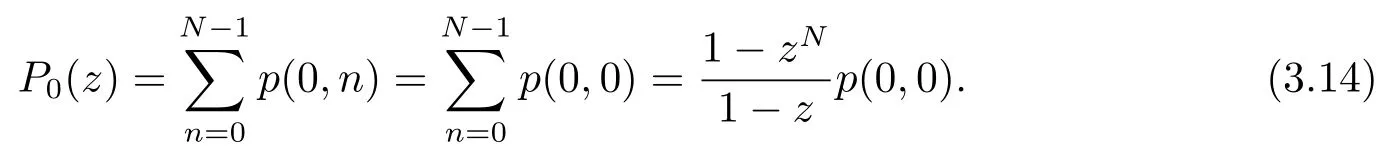
在(3.8)-(3.13)两边同时乘以z的幂次,然后分别相加求和,可得到下列方程组,

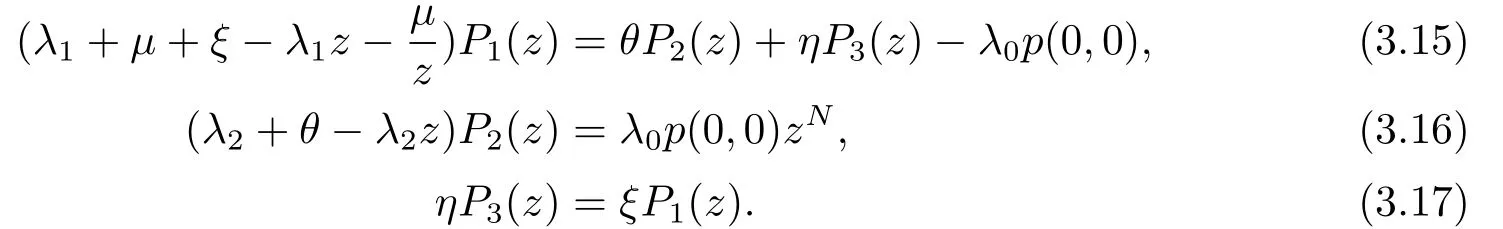
求解得

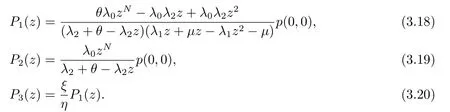
在(3.14),(3.18),(3.19),(3.20)中令z= 1,再由归一化条件可解出p(0,0),然后我们就得到了P0(1),P1(1),P2(1),P3(1),如(3.1)-(3.4)所示.

我们分别定义T(0,j),0≤j ≤N −1;T(1,j),j ≥1;T(2,j),j ≥N为标记顾客的平均逗留时间,该顾客到达时发现服务台状态为0,1,2,且他在系统中第j个位置.

引理3.2在带有N策略,启动时间和服务台故障的M/M/1排队系统中,标记顾客到达时发现服务台状态为0,1,2,且他在系统中第j个位置,那么他的平均逗留时间分别如下:

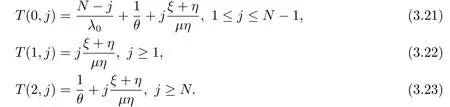
证首先,通过分析该排队模型,我们可得到以下方程:

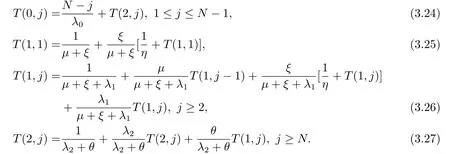
由(3,25)可得

由(3,27)可得

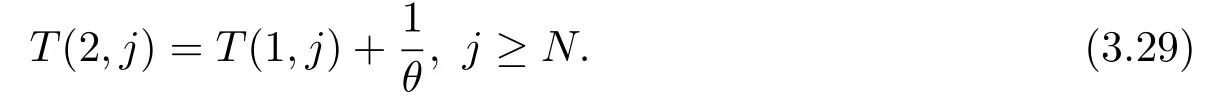
由(3.26)可得

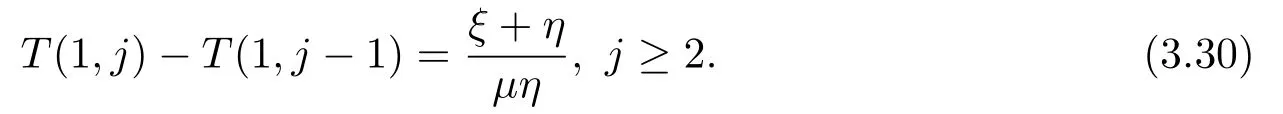
通过迭代(3.30),再结合(3.28)解出

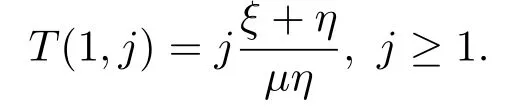
上式即(3.22).因此我们得到(3.21),(3.23).

定理3.1在带有N策略,启动时间和服务台故障的M/M/1排队系统中,给定到达率(λ0,λ1,λ2),当顾客到达时发现服务台状态为0,1,2的平均逗留时间分别如下:

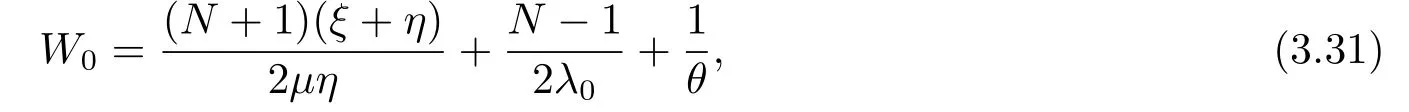
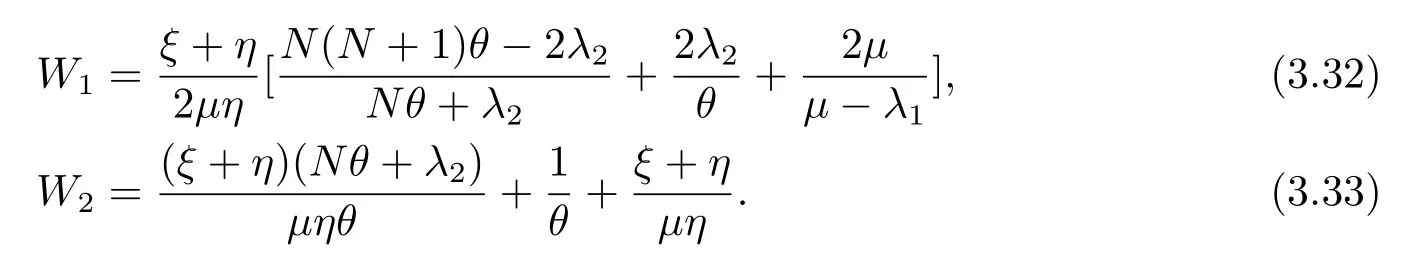
证定义W0(k)为一个到达顾客的平均逗留时间,该顾客到达时发现服务台状态为0,系统中顾客数为k,那么他就是系统中第k+1个顾客,由引理3.2可得W0(k)=T(0,k+1)=同时定义p(k|0)为顾客到达时发现服务台状态为0,系统中顾客数为k的概率,则那么当顾客到达时发现服务台状态为0的平均逗留时间为

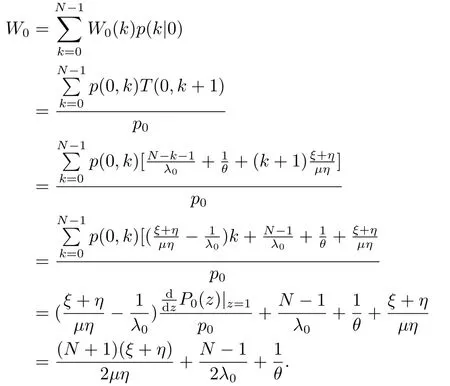
上式即(3.31).同理,当顾客到达时发现服务台状态为1,系统中顾客数为k,相应的平均逗留时间和条件概率为

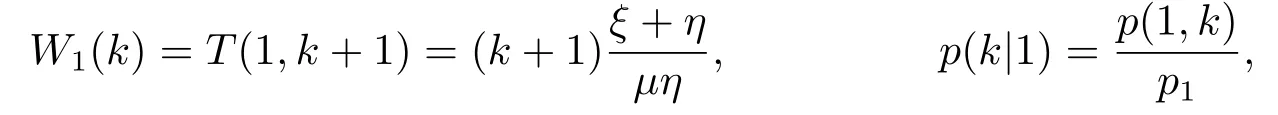
那么当顾客到达时发现服务台状态为1的平均逗留时间为

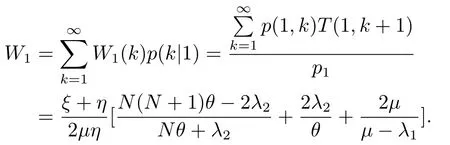
上式即(3.32).同理,当顾客到达时发现服务台状态为2,系统中顾客数为k,相应的平均逗留时间和条件概率为

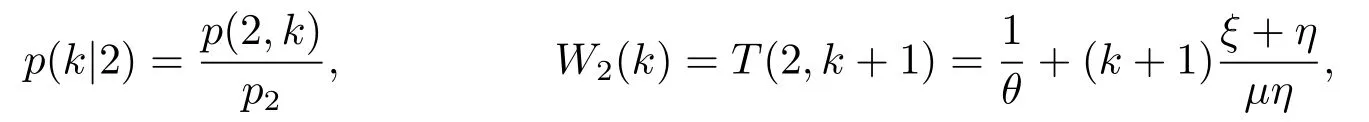
那么当顾客到达时发现服务台状态为2的平均逗留时间为

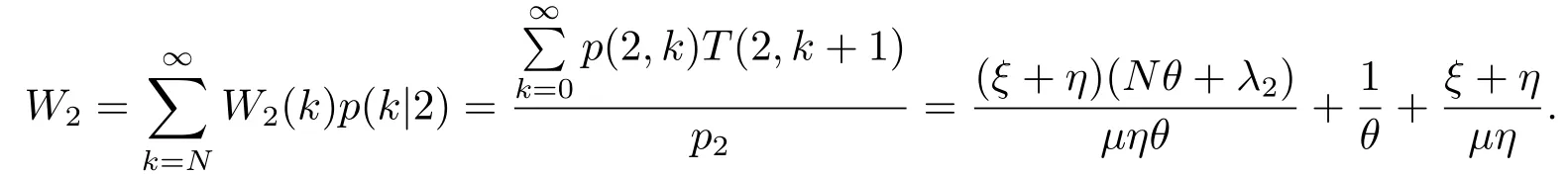
上式即(3.33).

显然,从定理3.1中我们能发现平均逗留时间W0(W2)与到达率λ1和λ2(λ0和λ1)独立,因此我们可以分别求相应的均衡到达率.另外,虽然W1只与λ0独立,但是一旦给定λ2,W1关于λ1是单调递增的,因此我们也能得到相应的均衡到达率.

令f(λ1,λ2)=W1.

定理3.2在带有N策略,启动时间和服务台故障的M/M/1排队系统中,当服务台状态为0时的均衡到达率

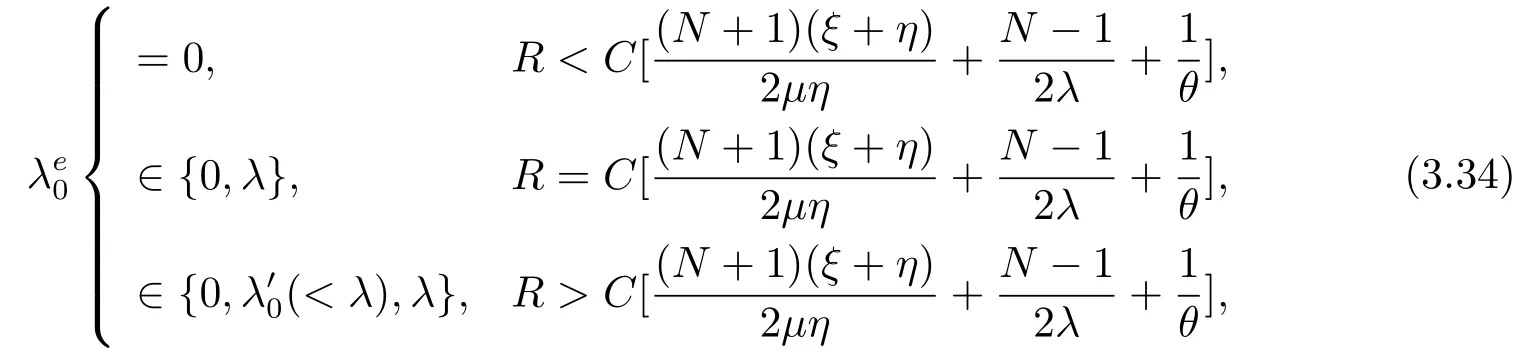
当服务台状态为2时的均衡到达率

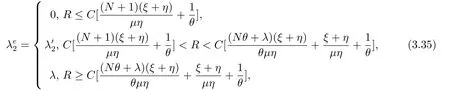
当服务台状态为1时的均衡到达率分三种情况,

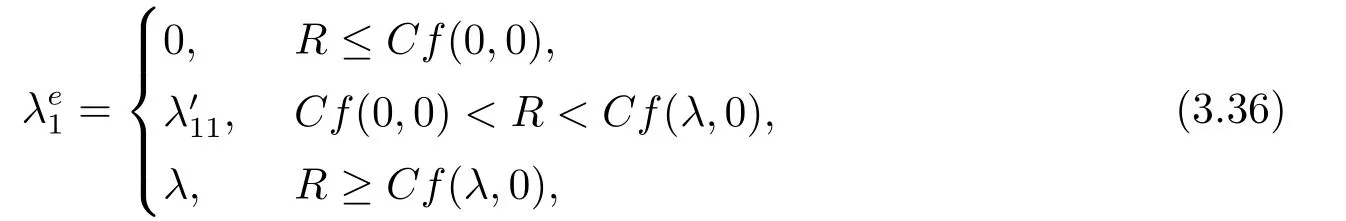
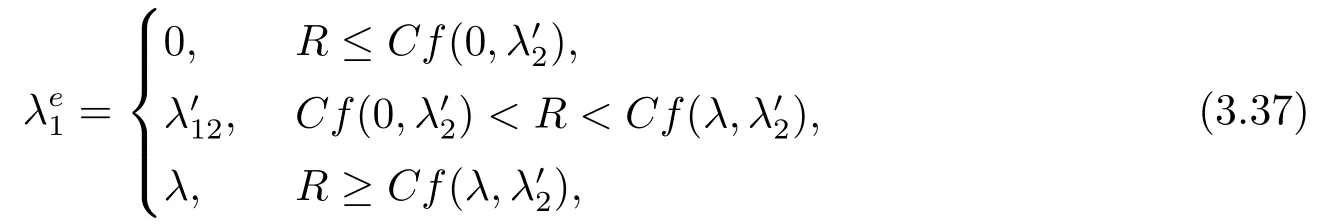
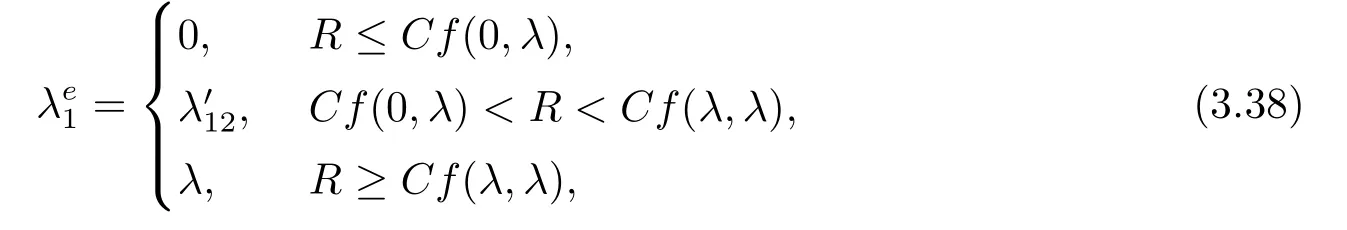
其中,

λ′11是R −Cf(λ1,0)=0的根,λ′12是R −Cf(λ1,λ′2)=0的根,λ′13是R −Cf(λ1,λ)=0的根.

证首先,发现服务台状态为0时止步始终是顾客的均衡策略,因为如果没有顾客决定进入系统,那么系统就不会启动,对于新来的标记顾客最优的响应也是选择止步,也就是说,λe0=0始终是顾客的均衡策略.

下面我们研究正的均衡到达率.根据收支结构,当顾客决定进入系统时,他的净收益等于报酬R和逗留成本的差值,因此根据定理3.1,他的净收益为

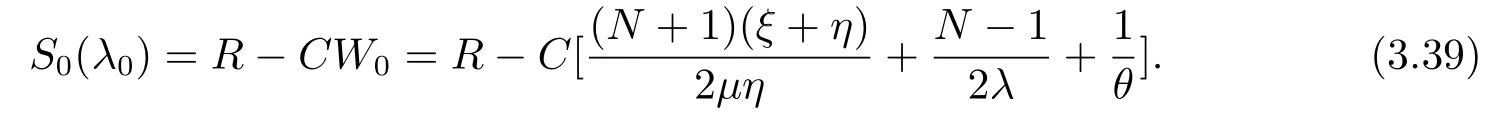
显然,S0(λ0)关于λ0∈[0,λ]递增,因此我们有以下结论:

同理,根据定理3.1,当服务台状态为2时,如果顾客决定进入系统,他的净收益为

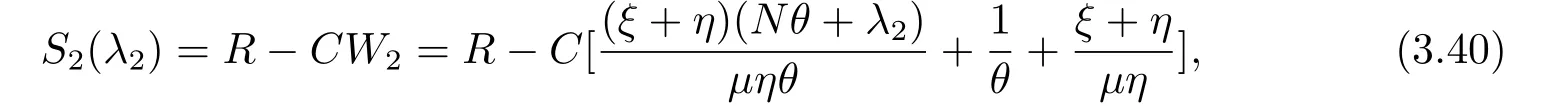
显然,S2(λ2)关于λ2∈[0,λ]递减,因此我们有以下结论:

同理,根据定理3.1,当服务台状态为1时,如果顾客决定进入系统,他的净收益为

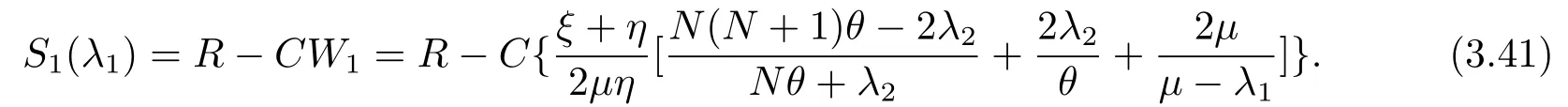
虽然W1只与λ0独立,但是一旦给定λ2,W1关于λ1是递增的,所以S1(λ1)关于λ1是递减的.从而(3.36),(3.37),(3.38)的证明与(3.35)的证明是类似的.

4.均衡社会收益

在这一节,我们给出了均衡社会收益函数.

命题4.1均衡社会收益函数

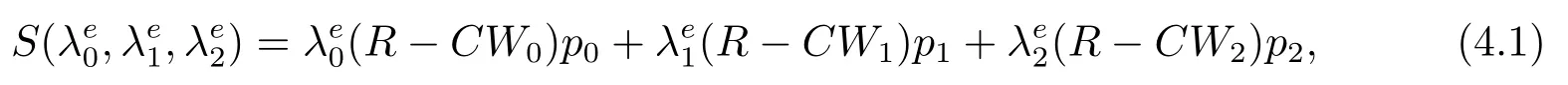
其中,

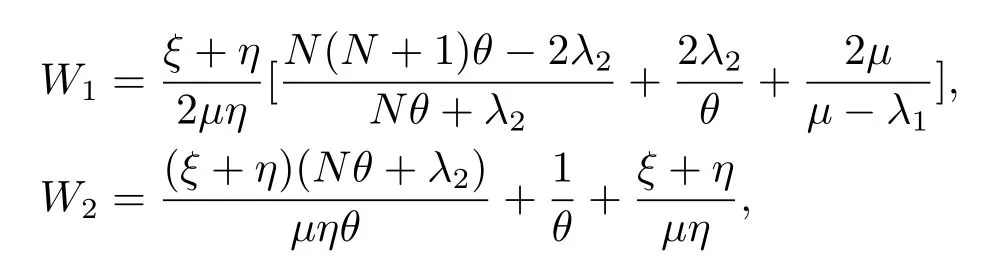
λ0,λ1,λ2分别由λe0,λe1,λe2代入,λe0,λe1,λe2在(3.34)-(3.38)中已给出.

5.数值分析

在这一节,我们分别研究一些系统参数(N,R,θ,µ,ξ,η)对均衡到达率λe0,λe1,λe2和均衡社会收益S(λe0,λe1,λe2)的影响.

首先我们研究了阈值N对均衡到达率和均衡社会收益的影响,结果如图2.根据图2(a),我们能发现当N较小时(N ≤6),λe0=λe1=λe2=1,随着N的增大,均衡到达率逐渐减小至零.这意味着当N较大时,顾客更倾向于止步.根据图2(b),我们可以看出均衡社会收益关于N是递减的.

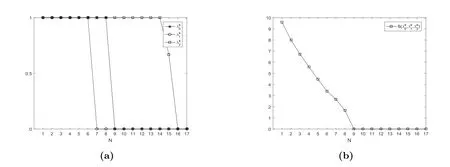
图2 均衡到达率λe0, λe1, λe2和均衡社会收益S(λe0,λe1,λe2)vs.N, 其中R=18, C =2,µ=ξ =η =2, λ=θ =1.

图3研究的是报酬R对均衡到达率和均衡社会收益的影响.在图3(a)中我们可以观察到当R较小时(R ≤7),λe0=λe1=λe2=0,并且λe0,λe1,λe2随着R的增大而增大.这意味着报酬R越大,顾客的净利润也会越大,他们就越倾向于进入系统.在图3(b)中也可以发现均衡社会收益随着R的增大而增大.

图3 均衡到达率λe0, λe1, λe2和均衡社会收益S(λe0,λe1,λe2)vs.R,其中N =4, C =2,µ=ξ =η =2, λ=θ =1.

在图4中,我们发现λe1=1,λe0和λe2关于参数θ递增.当θ较大时,机器的启动时间就较短,顾客的逗留时间随之减少,顾客就愿意进入系统.均衡社会收益关于参数θ也是递增的.

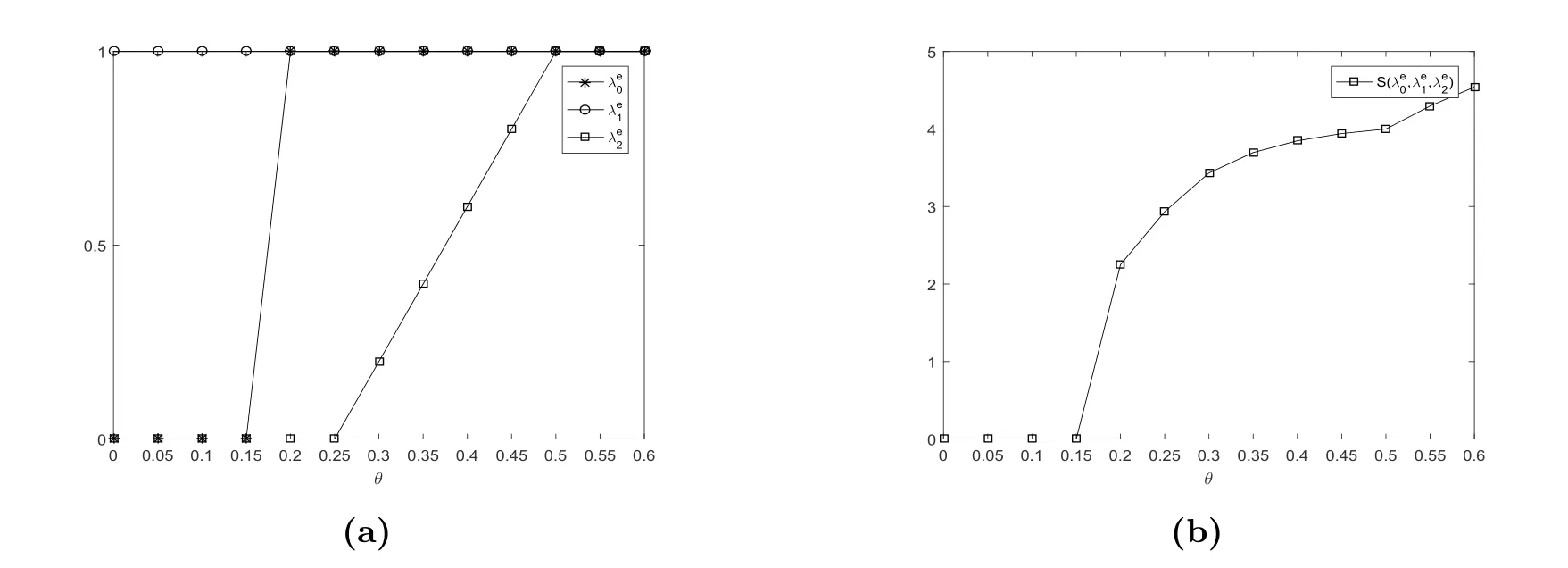
图4 均衡到达率λe0, λe1, λe2和均衡社会收益S(λe0,λe1,λe2)vs.θ,其中N =4, R=18, C =2,µ=ξ =η =2, λ=1.

根据图5,当µ >1时λe0= 1,λe1和λe2关于参数µ递增.当µ较大时,顾客的服务时间减少,逗留成本也就减少,顾客也就更愿意进入系统.显然均衡社会收益关于参数µ也是递增的.

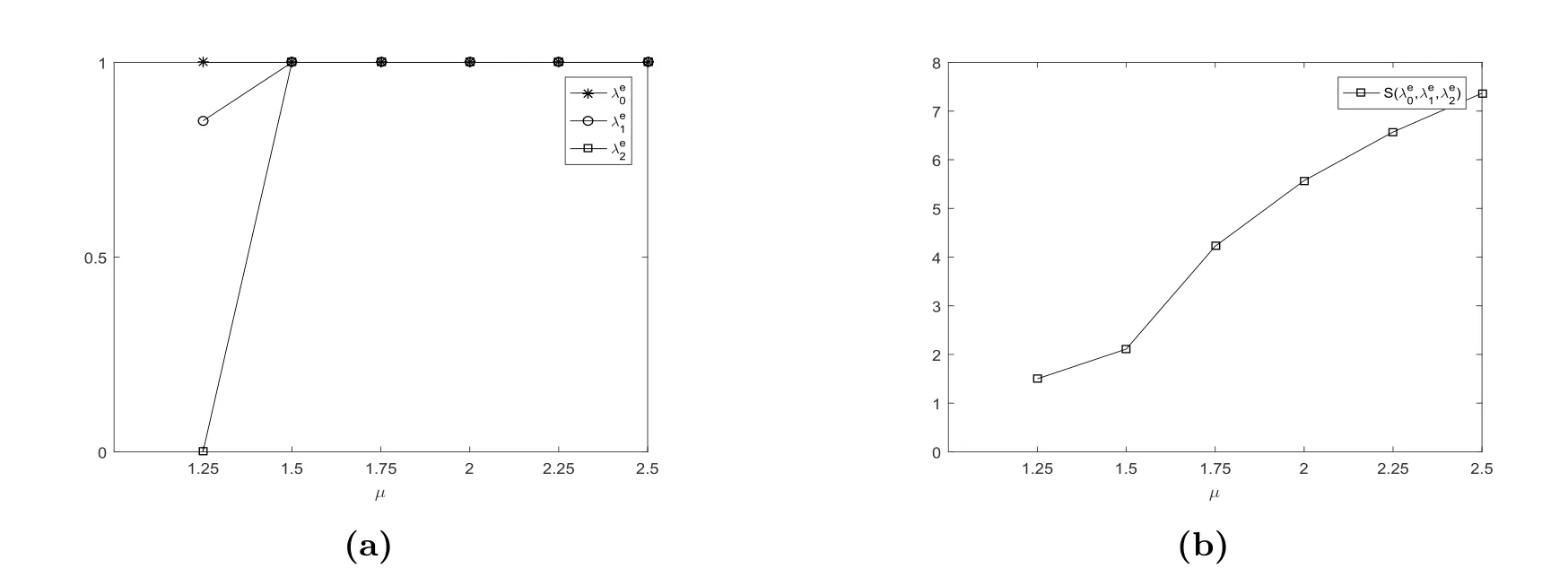
图5 均衡到达率λe0, λe1, λe2和均衡社会收益S(λe0,λe1,λe2)vs.µ,其中N =4, R=18, C =2,ξ =η =2, λ=θ =1.

图6研究了参数ξ对均衡到达率和均衡社会收益的影响.我们可以观察到随着ξ的增大,λe0,λe1,λe2逐渐减小至零.这意味着当ξ较大时,机器故障频率变大,顾客更倾向于止步.均衡社会收益也是随着ξ的增大逐渐减小至零.

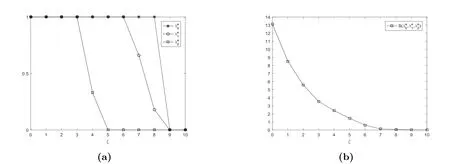
图6 均衡到达率λe0, λe1, λe2和均衡社会收益S(λe0,λe1,λe2)vs.θ,其中N =4, R=18, C =2,µ=η =2, λ=θ =1.

观察图7,我们可以发现λe0,λe1,λe2关于参数η递增.均衡社会收益关于参数η也是递增的.

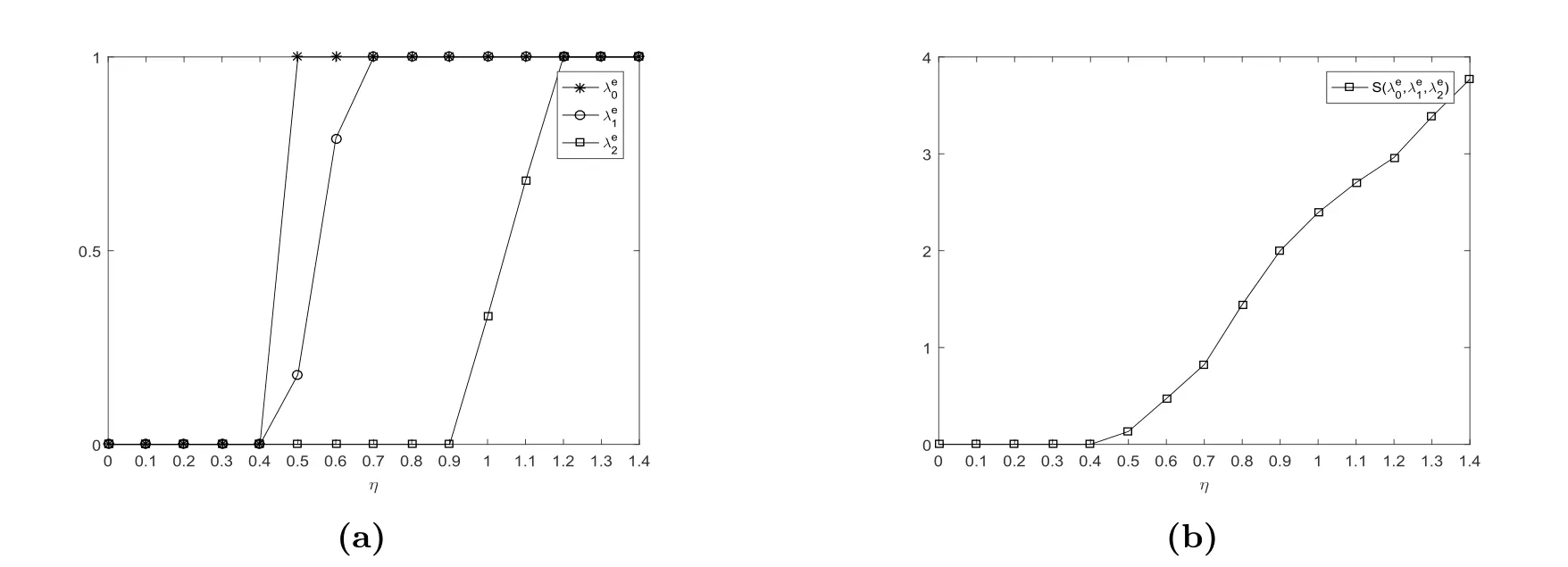
图7 均衡到达率λe0, λe1, λe2和均衡社会收益S(λe0,λe1,λe2)vs.θ,其中N =4, R=18, C =2,µ=ξ =2, λ=θ =1.