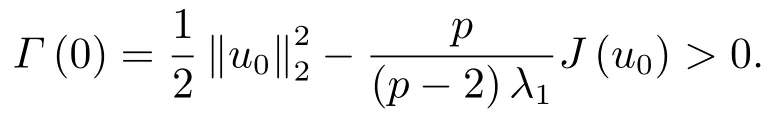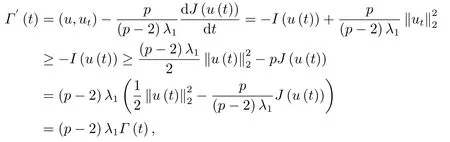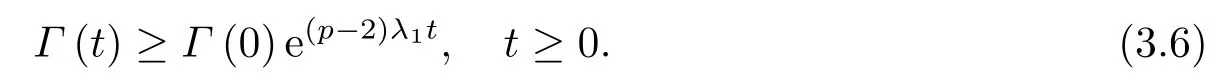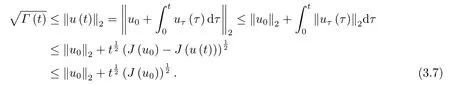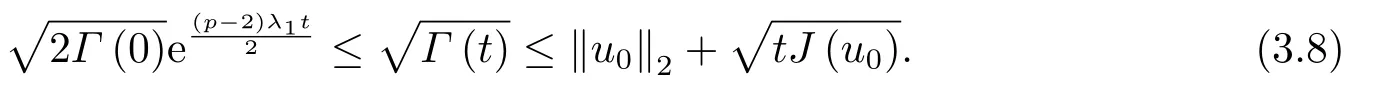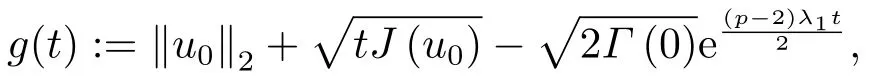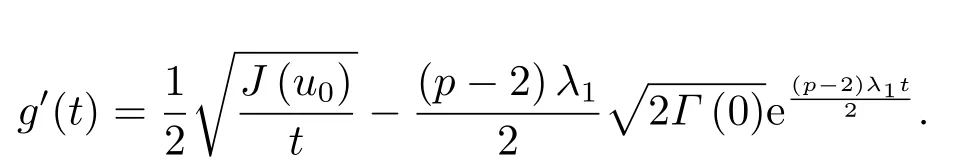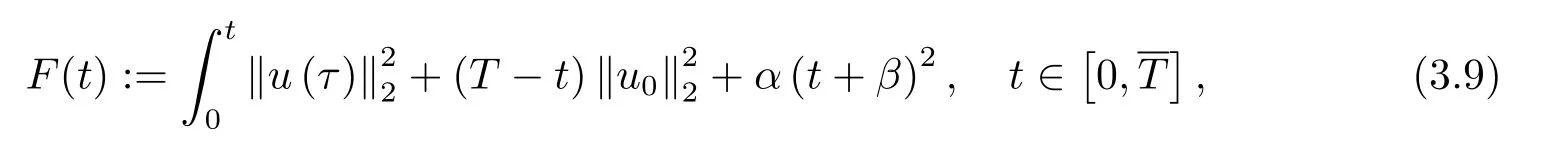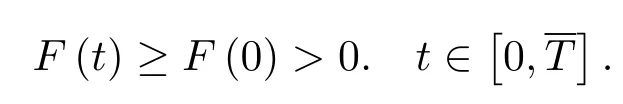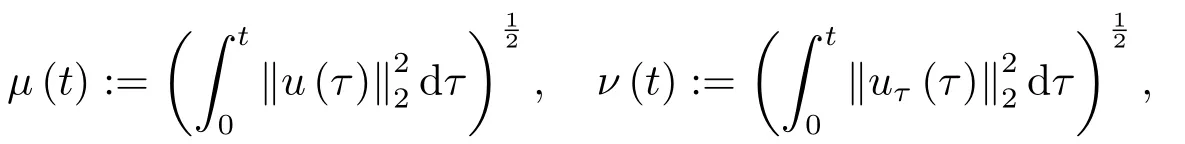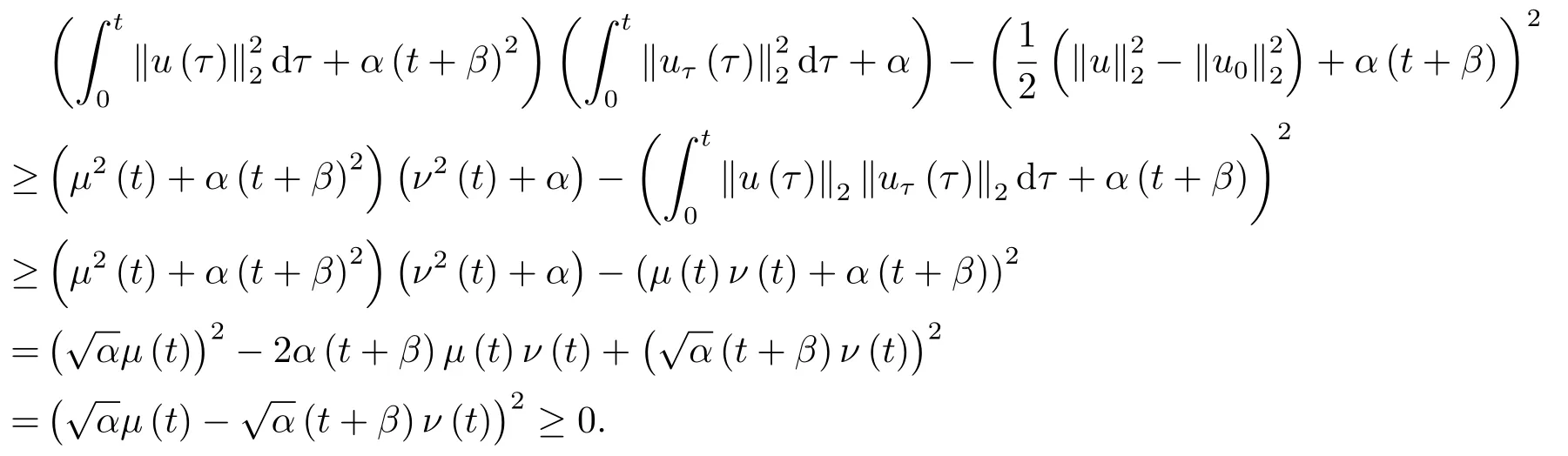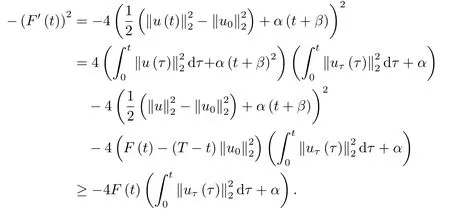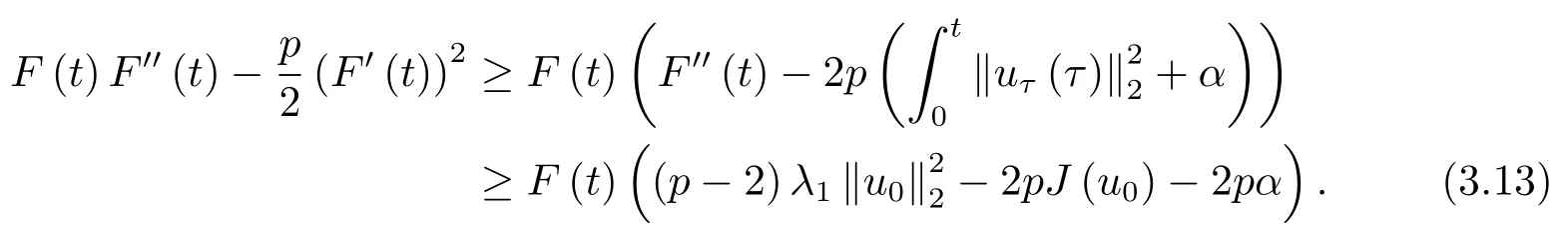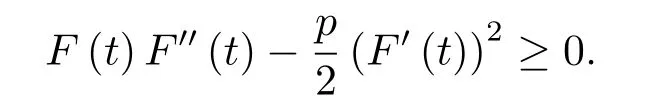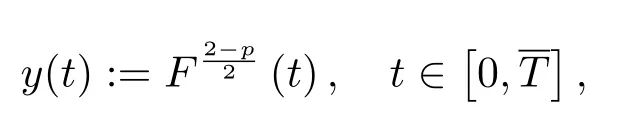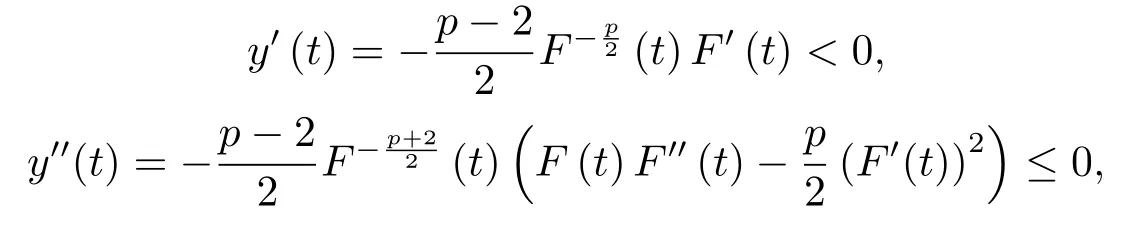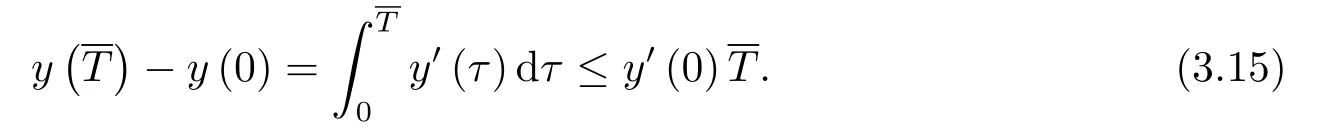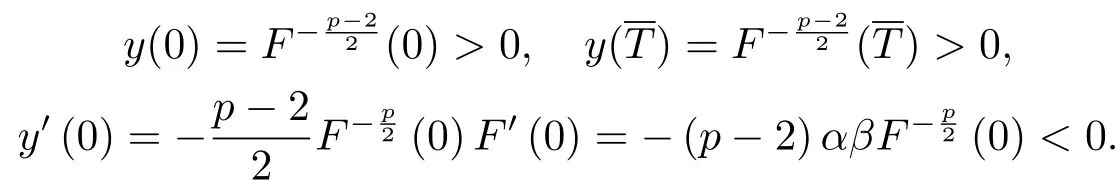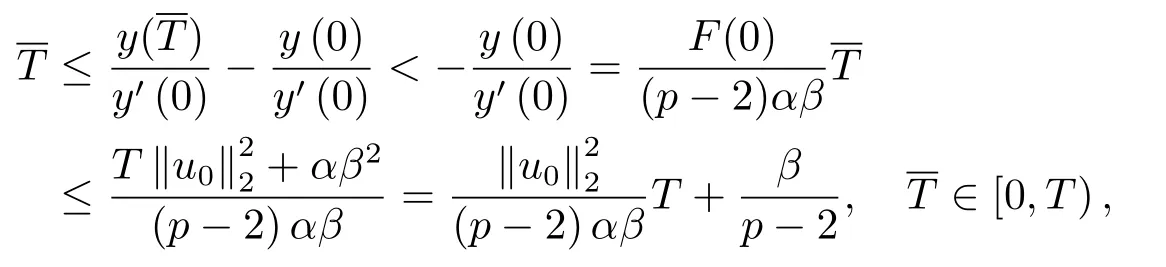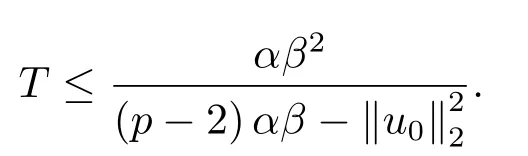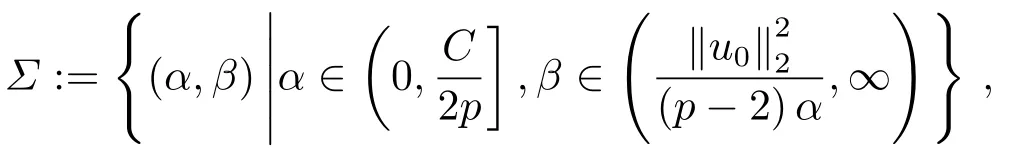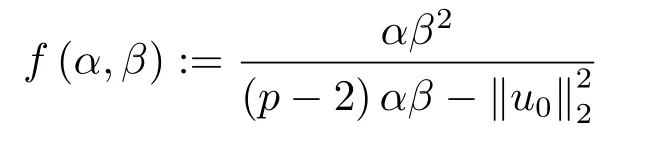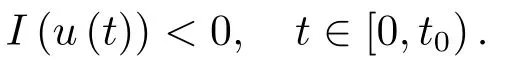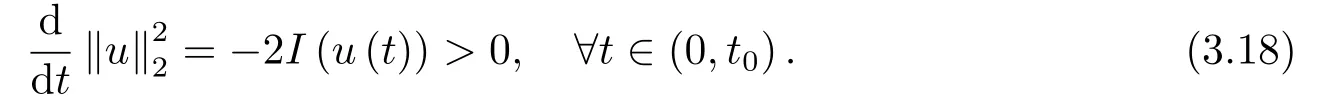一类具有对数非线性项的四阶薄膜方程新的爆破结果

赵元章,施明雨

(中国海洋大学数学科学学院,山东 青岛266100)

1.引言

我们考虑具有非线性对数源项的四阶薄膜方程

给出边界条件和初始条件

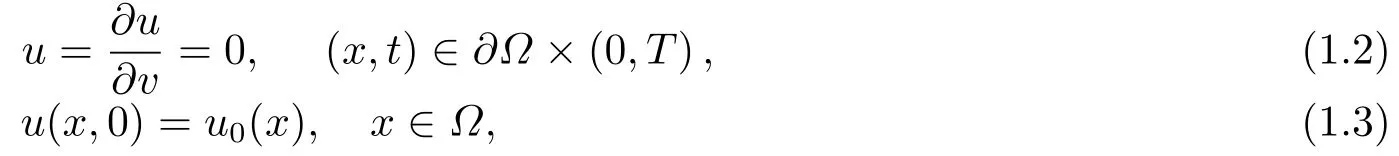
其中Ω ⊂RN(N ≥1)为具有光滑边界∂Ω的有界区域,v是边界∂Ω上的单位外法向量,初始值u0∈H10(Ω)∩H2(Ω),常数p满足条件

四阶薄膜方程(1.1)可描述许多物理过程,比如相变、薄膜的生长过程等都可用如下一般化的形式表达：

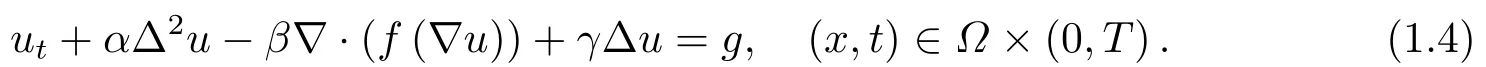
在外延薄膜生长理论中,u(x,t)表示外延生长中薄膜高度,α∆2u表示毛细驱动的表面扩散,−β∇·(f(∇u))表示原子的向上跳跃,γ∆u表示蒸发冷凝引起的扩散,g表示沉降通量.[1−3]

近些年来,许多学者致力于一般化的四阶抛物方程(1.4)初边值问题,比如,King等[2]考虑了如下四阶抛物型方程初边值问题

利用半离散逼近技巧,他们在适当的条件下建立了问题弱解的存在性、唯一性及正则性且导出了长时间行为.LIU[4−5]在一维和二维空间中考虑了齐次四阶拟线性抛物方程在零质量流边界条件下,他基于一致Schauder型估计和Campanato空间证明了问题整体古典解的存在性及正则性.

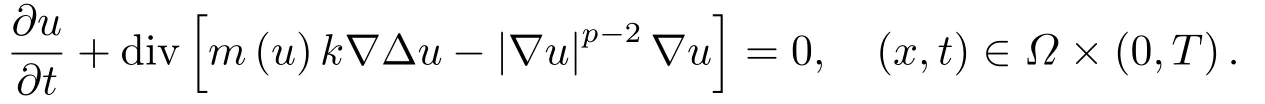
另一方面,当非齐次项g(x,t,u)关于u满足超或次线性增长条件(|u|s,s>1或s<1)且初值满足适当条件时,方程(1.4)的解可能会整体存在或有限时间爆破.XU等[6]研究了在高维空间中四阶半线性抛物方程初边值问题

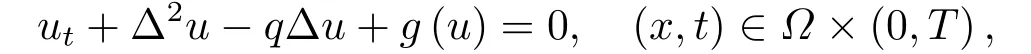
当g满足适当的结构性条件时,他们利用位势井方法及迭代技巧等建立了问题解的整体存在性与爆破、正则性及整体吸引子的存在性.最近,许多学者研究了如下具有质量守恒结构非局部源项的半线性四阶抛物方程初边值问题:

得到了解的整体存在性和有限时间爆破性以及解的长时间行为.在一维情形中,QU等[7]考虑了不含p-Laplacian项的半线性薄膜方程并利用位势井方法,得到了当初始能量满足次临界和临界的情形时问题变号解的整体存在性与非存在性的门槛结果及消失性质.紧接着,ZHOU[8]建立了具有正初始能量解的爆破结果并导出了爆破时间的上界.CAO和LIU[9]利用Galerkin方法及不等式技巧,对次线性增长条件情形证明了问题弱解的整体存在性及非消失性.LI等[10]考虑了在一维空间中含有p-Laplacian项的四阶抛物方程,他们利用位势井方法证明了在次临界初始能量和临界初始能量条件下给出了问题解的整体存在性、唯一性、有限时间爆破及渐近性质.DONG和ZHOU[11]延伸了文[10]的结果并得到了超临界初始能量情形.对高维情形(N ≥1),HAN[12]考虑了具有乘幂型源项的四阶抛物方程初边值问题并证明了在任意初始能量条件下问题解的整体存在性与有限时刻爆破及整体解的衰减估计值.在文[13]中,ZHOU针对文[12]中整体解的渐近行为做出了进一步延伸.

关于具有对数非线性项的发展方程的研究方面,最近也有一些新的起色且有许多成果.[14−19]从数学的角度来看,对数非线性项不满足单调性且可能变号,因此与具有乘幂型源项的问题相比较有着较大的难度.在文[14]中,HAN等研究了具有非线性对数项的四阶抛物型方程初边值问题

并借助于修正的对数Sobolev不等式和位势井方法,他们证明了在适当初值条件下整体解的存在性和无限时刻爆破及整体解的衰减估计.LIU和LIU[15]考虑了具有一般对数源项和Navier边界条件的半线性薄膜方程

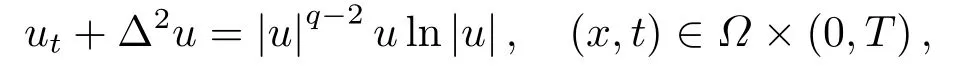
注意到,前述的大部分文献中主要采用的证明方法是位势井方法.位势井方法是Payne和Sattinger[20−21]于上个世纪60年代末研究双曲型方程初边值问题整体解存在性、稳定性与非稳定性时首次提出.此后,许多学者其推广和应用到各种非线性发展方程初边值问题解的整体存在性和非存在性问题,其中代表性的工作有见文[22-23].特别地,文[23]中引入了位势井族方法,解决了位势井的结构问题,并发现了非线性发展方程解在某些集合内不变性及解的真空隔离现象等.进一步,证明了具有临界初始条件解的整体存在性.但是,最大的缺点在于井的深度d太浅且其确切值很难计算.本文的主要目的在于探索问题(1.1)-(1.3)中与井的深度d无关的新爆破结论.事实上,类似于文[14-15],我们易得出当初始能量满足(其中α为任意正数且B为Sobolev嵌入常数)时问题(1.1)-(1.3)在适当的条件下弱解在有限时刻发生爆破.

本文剩余部分结构如下：第二章,我们给出一些记号、定义及主要定理证明过程中所需要的引理.第三章,我们给出主要结论的详细证明过程.

2.预备知识

本节中,我们引入一些记号、定义及主要结论证明所需的引理.

本文将用到一些记号.当1≤r <∞时,对任意u ∈Lr(Ω),∥u∥r表示u的Lr(Ω)范数,以(·,·)表示Lr(Ω)空间中的内积,记X:=H10(Ω)∩H2(Ω),X0:=X{0}.同时,由Poincaré不等式和带ε的Cauchy不等式可得

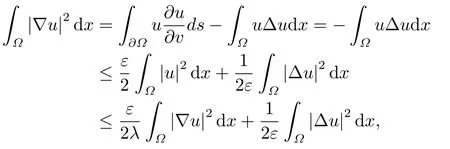
其中λ为−∆在Ω上固定边界薄膜振动问题的第一特征值,且令ε=λ,则我们有

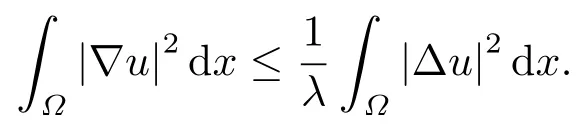
因此,空间X范数∥u∥X赋予等价范数∥∆u∥2.

对于任意的u ∈X,我们给出能量泛函J(u)和Nehari泛函I(u)定义

及Nehari 流形

我们定义位势井深度

则结合(2.1)和(2.2),我们有

下面,我们引入局部弱解及解的最大存在区间定义.

定义2.1令T0>0,假设u=u(x,t)∈L∞(0,T0;X),如果ut ∈L2(0,T0;L2(Ω)),u(x,0)=u0,且对任意φ ∈X有

则称u=u(x,t)∈L∞(0,T0;X),为问题(1.1)-(1.3)在Ω×[0,T0)上的弱解.

注意到,由Galerkin逼近技巧[14]易知问题(1.1)-(1.3)存在唯一弱解且u=u(x,t)∈L∞(0,T0;X),证明与文[14]中的定理3.1的证明类似,此处省略.

定义2.2假设u(t)为问题(1.1)-(1.3)的弱解,我们定义如下最大存在时间Tmax:

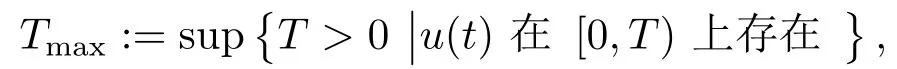
(i)如果Tmax<∞,我们说u(t)在有限时间爆破并且Tmax是爆破时间;

(ii)如果Tmax=∞,我们说u(t)是整体存在的.

紧接着,给出我们主要结论证明所需的引理.

引理2.1 对u ∈X0和正实数λ>0,如下断言成立:

(ii)存在唯一的λ∗=λ∗(u)>0使得并且J(λu)在0<λ <λ∗上单调递增;在λ∗<λ<+∞上单调递减;当λ=λ∗时,J(λu)取得最大值;

(iii)当0<λ<λ∗时,I(λu)>0;当λ∗<λ<+∞时,I(λu)<0;当λ=λ∗时,I(λ∗u)=0.

证对u ∈X0,根据能量泛函的定义(2.1)有

则

我们令

并直接计算可得

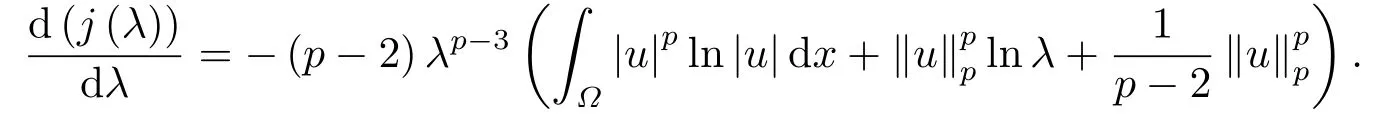
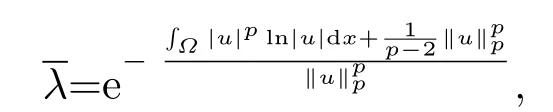
满足j(λ)在上递增;在上递减.再由易知,存在唯一λ∗>,使得j(λ∗)=0,且当0<λ<λ∗时,j(λ)>0;当λ∗<λ<+∞时,j(λ)<0.因此,J(λu)在0<λ<λ∗上单调递增；在λ∗<λ <+∞上单调递减；当λ=λ∗时,J(λu)取得最大值.显然(i)和(ii)成立.

关于结论(iii),结合(2.2)和(2.6)可得出

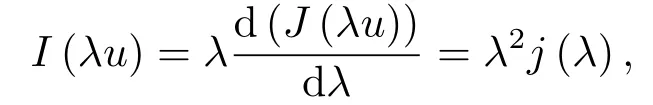
且易知,结论(iii)显然成立.引理2.1证毕.

注2.1引理2.1中,(iii)表明N非空.

现在,我们记λ1为特征值问题

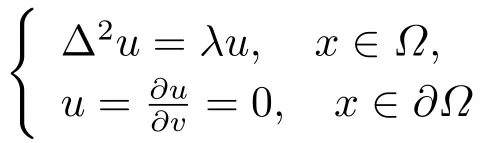
的第一特征值.则由文[24]知λ1>0且

同时,定义新的能量泛函

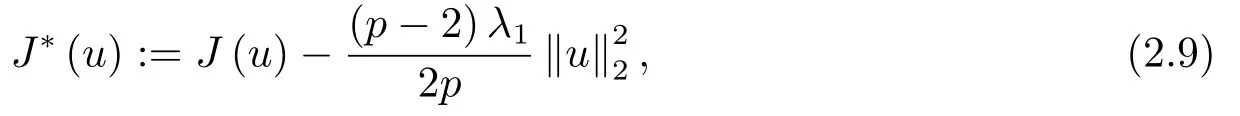
并定义如下集合：

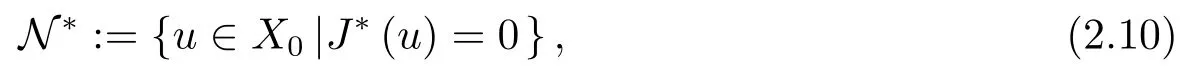
类似于引理2.1,我们易得到如下引理：

引理2.2对u ∈X0,存在唯一的λ∗>0使得λ∗u ∈N∗;当0<λ <λ∗时,λu ∈N∗+;当λ>λ∗时,λu ∈N∗−.

由集合N和N∗的定义,我们可得到引理.

引理2.3假设N和N∗分别如(2.3)和(2.10)式定义,则有N ∩N∗=∅.

证利用反证法,假设存在u=N ∩N∗,则u ∈N且u ∈N∗.对u ∈N由Nehari流形的定义(2.3)易知,u ∈X0且I(u)=0.结合(2.5)和(2.8),我们得到

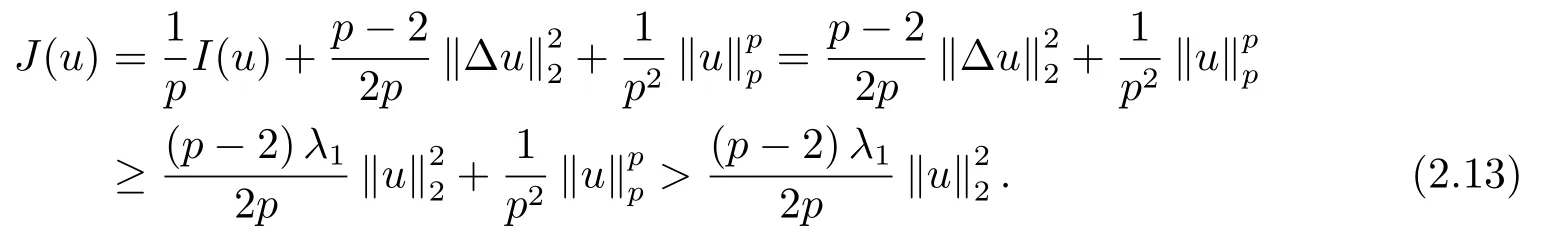
对u ∈N∗.由集合N∗定义(2.10)易知,u ∈X0且J∗(u)=0.由(2.9)得到

显然,(2.13)与(2.14)导致矛盾且N ∩N∗=∅.引理2.3证毕.

引理2.4设u=u(t)为问题(1.1)-(1.3)的弱解,则J(u(t))关于t是非增函数.

证对J(u(t))直接求导,我们得到

在定义2.1 中取φ=ut,我们有

且易知

引理2.4 证毕.

3.主要结论

本节中,在之前的研究中爆破结果密切依赖于位势井深度d的大小,但是d的准确数值很难计算.因此,本节中我们建立一个不依赖于d的爆破条件.

定理3.1假设常数p满足条件(P),u0∈X且满足

如果u(x,t)是问题(1.1)-(1.3)的弱解,则u(x,t)在有限时刻T发生爆破且满足

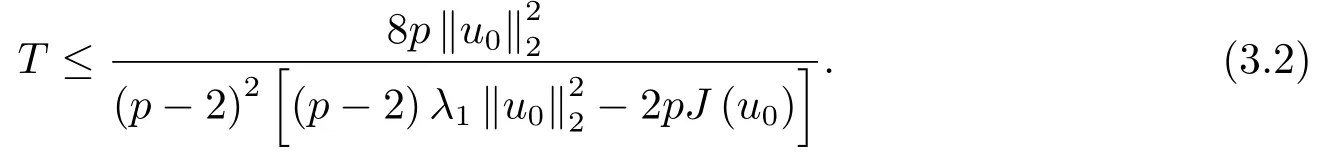
证由(2.1),(2.2),(2.8)和(3.1)式,我们得到

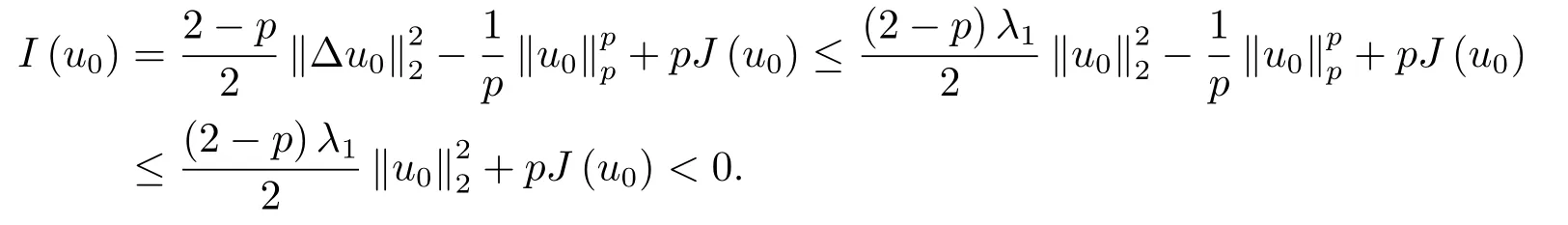
紧接着,我们利用反证法证明对所有的t ∈[0,T)有

假设结论不成立,则必然存在t0∈(0,T)使得

且

现在,由(3.4)可得u(t0)∈N.同时,结合(2.5),(2.8),(3.1)和(3.4)可得

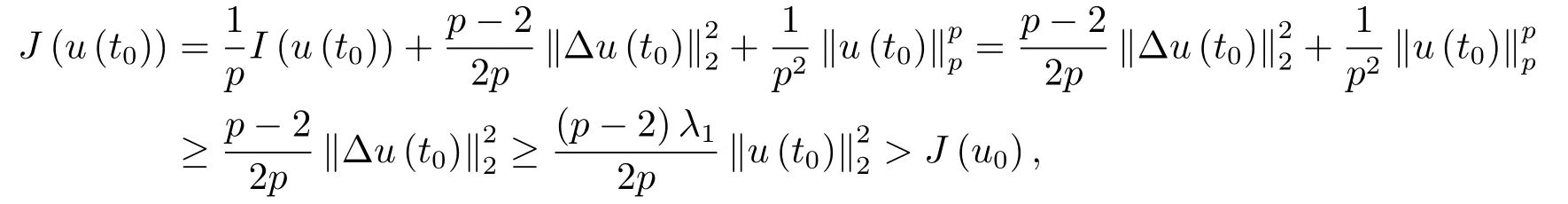
且与引理2.4导致矛盾.因此,对所有的t ∈[0,T)有I(u(t))<0.

下面,我们只需考虑J(u(t))≥0的情况.事实上,如果存在t1使得J(u(t1))<0,则由(3.3)易知,J(u(t1))

于是,当J(u(t))≥0时,我们再次利用反正法证明u(t)是非整体存在的,即解在有限时刻发生爆破.假设u(t)是整体存在且我们定义函数

由条件(3.1)易知

对(3.5)直接求导并结合(3.4)和(3.5),我们有

且利用Gronwall不等式可得

另一方面,利用Hölder不等式和J(u0)≥J(u(t))≥0,我们得到

综合(3.6)和(3.7),我们可得

现在,我们定义函数

并直接求导得到

显然,当t →0+时g′(t)>0,且存在T1>0使得g′(T1)= 0,当t ∈(0,T1)时,g′(t)>0;当t ∈(T1,∞)时,g′(t)<0.另一方面,由g(0)>0易知,存在充分大的T >T1,使得g(T)= 0,且当t ∈(T,∞)时,g(t)<0因此,与(3.8)导致矛盾,即u(t)是在有限时刻发生爆破.

最后,我们给出爆破时间T的上界估计值.首先,对任意的,我们定义如下函数：

其中α,β为待定正常数.显然,我们有

且对(3.9)式直接求导得到

且满足

然后,对(3.9)式求二阶导数,并结合的I(u(t))定义和(2.8)式,我们导出

另外,为了表达方便,我们记:

则经过简单的计算并利用Hölder不等式,我们得到如下不等式成立：

因此,我们直接计算得到

再结合(3.12),我们导出

现在,我们选取α足够小,使得

其中

则由(3.13)易知

我们再定义如下函数：

且直接求导,我们有

且易知

同时,由y(t)的定义和(3.11)有

因此,由(3.10)和(3.15)得到

且取极限T →T有

我们选取β足够大使得

则有

现在,由(3.14)和(3.16)如下定义集合：

且有

下面,我们定义函数

且求下确界.

显然,对固定的β,f(α,β)关于α在单调递减;对固定的α,f(α,β)在处取最小值,所以有

定理3.1证毕.

定理3.2假设常数p满足条件(P),u0∈X且满足

如果u(x,t)是问题(1.1)-(1.3)的弱解,则u(x,t)将在有限时刻发生爆破.

证令u0∈X且满足为相应的弱解且它的最大存在时间为T.

首先由(2.1)、(2.2)、(2.8)和(3.17)式,我们得到

我们可以断言I(u0)<0.事实上,如果I(u0)= 0.则u0∈N且我们有u0∈N ∩N∗,这与引理2.4矛盾.

紧接着,我们利用反证法证明对所有的t ∈[0,T)有I(u(t))<0.

假设结论不成立,则必然存在t0∈(0,t)使得

且

则在定义2.1中取φ=u,我们有

再结合(2.5),(2.8)和(3.18)可得

且与引理2.4导致矛盾.因此,对所有的t ∈[0,T)有I(u(t))<0.接下来,我们对J∗(u(t))直接求导有

又因为J∗(u0)=0,所以必然存在t1>0使得J∗(u(t1))<0,即

如果我们假设t1为初始时刻,则类似于定理3.1的证明过程易知,u在有限时刻发生爆破.