基于多域特征的滚动轴承故障检测和状态识别方法

李大江

(广东铭安职业安全技术检测有限公司，广东 广州 510045)

滚动轴承是旋转机械中应用最广的零部件之一，其工作状态直接影响着整个机器设备的性能。与其他零部件相比，滚动轴承工作环境恶劣，并且长期处于连续运转状态，是机器中故障率最高的零部件[1]，因此对滚动轴承的工作状态进行早期检测和故障诊断对于保证机器的安全、稳定运行具有重要意义[2]。

滚动轴承故障时产生的振动信号是一种典型的非平稳、非线性信号，因此很多非平稳、非线性信号特征检测方法如小波变换、经验模态分解、局部均值分解等都被应用于滚动轴承早期故障诊断领域。刘霞等[3]采用小波变换将信号转换到时频域并提取奇异熵特征进行滚动轴承故障检测，但是小波基函数的选择和分解层数的确定对结果影响较大；胡爱军等[4]采用集成经验模态分解对滚动轴承故障信号进行分析，并根据峭度准则提取特征实现故障检测；刘震坤[5]、徐乐等[6]将局部均值分解方法应用到滚动轴承故障检测领域，提取能量熵特征对正常和故障滚动轴承振动信号进行区分。

上述研究方法都是从某个特定的变换域对滚动轴承振动信号进行分析，提取的特征较为单一，没能包含不同维度的信息，具有一定的局限性。本文提出一种基于局部均值分解(local mean decomposition, LMD)和共空间模式(common spatial pattern, CSP)的时-频-空多域特征提取方法,实现对轴承外圈故障、内圈故障和滚柱故障3种状态的分类,相对于单一特征具有更高的分类性能。

1 基于LMD和SVDD的故障检测

1.1 LMD算法

LMD是由Jonathan S.Smith提出的一种自适应非平稳信号分析方法，能够将复杂多分量信号分解为若干个瞬时频率具有物理意义的乘积函数(product function,PF)和的形式，对于滚动轴承故障引起的振动信号x(t)，t=1,2,…,T,t为采样时间，T为总采样时间。对其进行LMD分解过程可以总结为：

1)利用x(t)的所有极值点ni,计算得到均值序列mi和包络估计序列ai，其中i=1,2,…,O，O为极值点总个数。

(1)

利用滑动平均法分别对mi和ai构成的曲线进行平滑处理，得到局部均值函数m11(t)和包络估计函数a11(t)。

2)从原始信号中减去局部均值函数m11(t)，得到差值信号h11(t)，即

h11(t)=x(t)-m11(t)

(2)

3)根据式(3)对差值信号进行幅度解调，得到调频信号x11(t)，即：

(3)

对x11(t)的包络估计函数a12(t)进行分析，如果a12(t)=1，则x11(t)为纯调频信号，否则将x11(t)作为初始输入信号重复以上步骤，直到a12(t)=1。

4)将得到的所有包络估计函数相乘，得到幅值函数a1(t)，即

(4)

式中：a1q(t)为第q个包络估计函数，q=1,2,…,j，j为包络估计函数的总个数。

5)将a1(t)与x11(t)相乘得到第一个PF分量f1(t)，即

f1(t)=a1(t)x11(t)

(5)

6)从原始信号中减去f1(t)得到剩余信号u1(t)，即

u1(t)=x(t)-f1(t)

(6)

7)令x(t)=u1(t)，重复步骤1)～步骤6)，直至获得所有L个PF分量fl(t),l=1,2,…,L，且剩余信号uL(t)为单调函数时迭代终止，此时原始信号经过LMD分解后可以表示为：

(7)

1.2 时-频熵特征

熵是信息论中用来衡量系统不确定度的一种物理量，振动信号经LMD分解后，每个PF分量都从不同维度对原始信号的时-频分布特性进行了描述，定义第l个PF分量fl(t)的时-频波形熵特征Hl为：

(8)

(9)

1.3 基于SVDD一类分类器的故障检测

在实际工程实践中，事先往往只能得到轴承在正常工作状态下的振动数据，没有足够的故障数据进行分析，因此本文采用支持向量数据描述(support vector data description, SVDD)一类分类器[7]对轴承是否正常进行检测。

对正常工作状态下的振动数据根据式(9)提取LMD时-频熵特征向量U,U={F1,F2,…,FN},其中Fn为第n组数据的时-频熵特征，n=1,2,…,N,N为训练样本集大小。SVDD通过在高维空间中寻找球心为e、半径为r的最小体积超球体B(c,r)，使其包含尽可能多的训练样本，SVDD通过求解如下优化问题得到最小超球体：

(10)

式中：xi为支撑向量；c为平衡参数；ξi为松弛变量。在得到最小超球体后，对于未知样本F*，其决策方程为：

f(F*)=‖F*-c‖2-r2

(11)

若f(F*)≤0，即F*在最小体积超球体内时，F*为目标样本，否则F*为异常样本。

2 基于CSP和K-均值的故障状态识别

上述LMD时-频熵特征和SVDD一类分类器仅实现了对滚动轴承是否故障的判断，如果能够进一步对故障状态进行分类识别，可以帮助人们最大程度地发挥滚动轴承的工作效率和潜能。本文针对3种最常见的滚动轴承故障(外圈故障、内圈故障和滚柱故障)进行分析，在LMD分解的基础上，采用CSP进行空域特征提取，并构建时-频-空多域特征向量对3种故障状态进行描述，最后采用K-均值聚类算法对3种故障状态进行自适应聚类。

2.1 基于CSP的空域特征提取

滚动轴承故障发生位置不同会产生不同的故障振动信号，因此空域特征能够较好地对不同故障状态进行描述。CSP是一种经典的多通道空域滤波方法，能够有效提取信号的空间分布特性，因此本文将LMD分解得到的L个PF分量作为CSP的多通道数据进行分析并提取空域特征。

1)利用L个PF构建多通道信号矩阵E=[f1(t),f2(t),…,fL(t)]。

2)计算协方差矩阵R：

(12)

式中：trace(·)为对括号内矩阵进行求迹运算。

3)对协方差矩阵进行特征值分解：

R=UΣU

(13)

式中：U为R特征向量构成的矩阵；Σ为对应特征值构成的对角矩阵。

4)计算白化矩阵P，并利用其对协方差矩阵做白化处理得到矩阵S：

(14)

5)对白化后矩阵S进行特征值分解并构造空间滤波器W：

(15)

式中：U1为S特征向量构成的矩阵；Σ1为对应特征值构成的对角矩阵；P为右对角矩阵。

6)利用空间滤波器W对信号矩阵E进行空域滤波得到特征矩阵Z：

Z=WE

(16)

对特征矩阵对角线元素提取空域熵特征b：

(17)

2.2 基于K-均值的时-频-空多域特征聚类

在前述分析的基础上，将LMD分解得到的时-频熵特征和CSP分解得到的空域熵特征构成时-频-空多域特征向量s=[F,b]，该特征向量能够从时-频-空3个维度对滚动轴承故障状态的特性进行描述，用来实现对故障状态的分类识别。

K-均值聚类算法由于具有理论简单、实现容易、计算效率高等特点，成为了当前应用最为广泛的非监督类模式分类方法之一。对于本文涉及的3类滚动轴承故障状态分类问题，K-均值聚类算法步骤可以总结为：

1)设置聚类个数K=3，并从特征向量集中随机选取3个样本作为初始聚类中心u1,u2,u3；

2)计算数据集中每个样本到聚类中心的欧氏距离并将其划分至距离最近的类别中；

3)根据式(16)计算得到新的3个聚类中心；

4)按K个新聚类中心对样本集进行重新划分，若连续两次得到的划分结果一致，则算法收敛，否则重复上述步骤。

3 算法流程总结

图1给出了本文所提滚动轴承故障检测和状态识别的流程图，可以看出算法从左到右可以分为训练和测试两个阶段。

4 实验结果及分析

为了验证所提方法对滚动轴承故障检测和状态识别的有效性，采用1只正常轴承、1只外圈故障轴承、1只内圈故障轴承和1只滚柱故障轴承在相同条件下开展实验，轴承型号为N206，采用ADA16-8/2板卡对4只轴承工作过程中的振动数据进行采集，采样频率为4 100 Hz，对每只轴承分别采集100组数据构成数据集，即数据集容量为400，每组数据的采样点数为800。实验中，随机选取正常状态下的70组数据作为训练样本，对SVDD分类器进行训练得到最优分类面，剩余30组正常数据和300组故障数据作为测试样本开展实验。

图1 所提算法流程图

按照1.2节介绍的时-频熵特征提取方法对所有330组样本提取特征得到统计结果，见表1。可以看出，正常状态下滚动轴承振动信号时-频熵特征的均值明显高于其余3种故障轴承，原因在于正常状态下滚动轴承工作时振动信号的时-频分布较为稳定和平均，因此时-频熵特征值较大，而当滚动轴承出现故障时，其运行过程中振动信号的时频分布会出现聚集，即在对应时域和频域的能量较大，不确定性降低，因此时-频熵特征值较小。

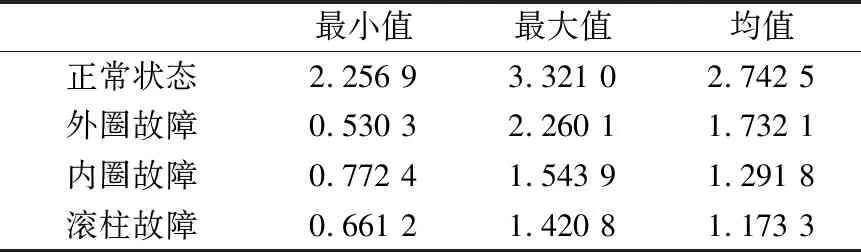
表1 时-频熵特征值

同时从表1可以看出，3种故障状态下时-频熵特征的均值虽然存在一定的差异，但是从最小值和最大值的分布可以看出，3种故障状态时-频熵特征值的取值范围存在一定的交叠。

根据图1所示算法流程，利用70组正常状态下的数据对SVDD进行训练，得到最优分类面后对剩余数据进行测试得到的结果见表2。可以看出基于LMD和SVDD的故障检测方法对正常状态可以获得96.7%的检测正确率，对故障状态可以获得99.3%的检测正确率。

表2 基于时-频熵特征和SVDD的故障检测结果

上述结果表明，基于LMD分解的时-频熵特征能够有效表征滚动轴承在正常和故障时振动信号在时-频域的分布特性差异，但是对于不同故障状态振动信号的时-频域分布差异特性不能有效区分。

为了进一步对3种故障状态进行分类识别，根据图1所示算法流程对SVDD判决为故障的数据(共299组，含1组正常状态数据)采用CSP进行分析并提取空域特征，图2给出了采用K-均值对时-频-空多域特征向量进行聚类得到的结果，可以看出在时-频-空多域特征空间，3种故障状态数据呈现出了较高的可分性。表3给出所提方法和采用单一维度能量熵特征进行识别的结果对比。可以看出，所提方法对每类故障状态的识别正确率都高于80%，明显优于单一维度能量熵特征。

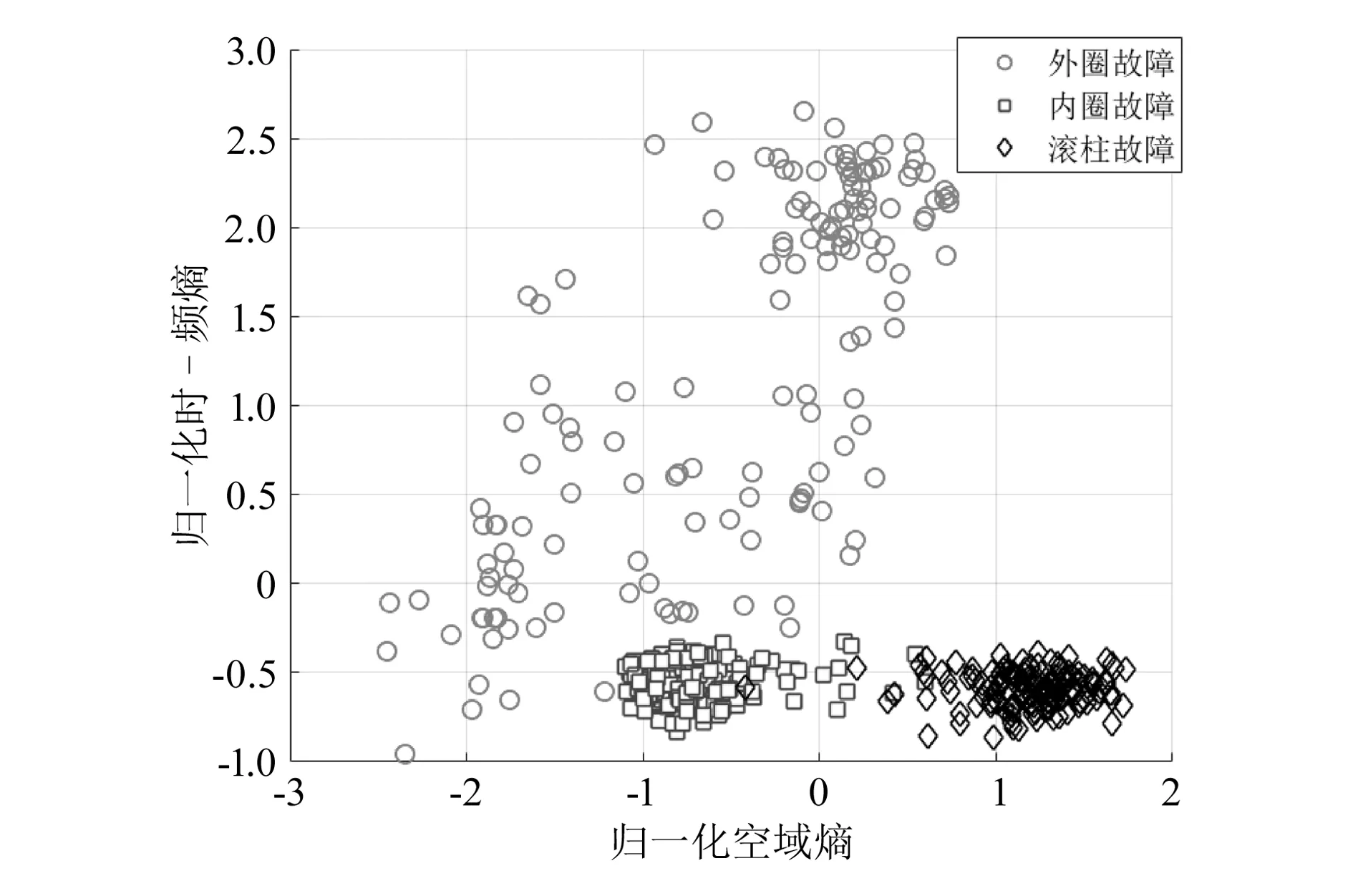
图2 K-均值聚类结果

表3 故障状态识别结果 %

5 结束语

针对滚动轴承故障时产生的振动信号非平稳、时变和微弱性的特点，本文提出一种基于时-频-空多域特征提取的滚动轴承故障检测和状态识别方法，充分利用了轴承故障信号在不同特征域的差异信息实现外圈故障、内圈故障和滚柱故障3种状态的有效识别。实测数据表明，所提方法相对于单一特征能够获得更高的故障检测和状态识别结果。