薄膜声学超材料低频隔声研究
2021-04-16胡超楠林国昌姚永涛
袁 伟,胡超楠,林国昌,姚永涛
(1.上海飞机设计研究院,上海 201210) (2.特种环境复合材料技术国防科技重点实验室,黑龙江 哈尔滨 150001)
噪声充斥于日常生活与工程应用的各个领域。日常生活中的噪声不但会影响人们的日常工作与学习,还会影响人类的健康;而工程应用领域的噪声会影响设备的使用,缩短使用寿命,造成财产损失,甚至会导致严重的事故,因此降低噪声尤为重要。
当传播的声波经过障碍物时,会发生反射、透射和能量损耗等一系列过程导致声能降低,这个过程称为隔声。在隔声领域,高频噪声属于易于隔离的频段噪声,使用传统材料隔音板或隔音墙便可达到良好的隔声效果。低频噪声具有波长大、极具穿透性、传播距离远等特点,由于质量定律的作用,与高频隔声相比,传统隔声材料需具有更大的宏观尺寸,使得成本增加,空间占用增大,且隔声效果差。
近年来,声学超材料的提出为解决这一难题提供了新思路。在声学领域,人为设计和构造声学结构,使其具有自然材料所不具备的特殊功能,从而有效地调控声波,这种人工制造的材料被称为声学超材料。声学超材料是具有负等效质量密度和负等效体积模量的人造亚波长结构,可实现特殊的声波特性,如声波的负折射、声聚焦、超透镜、声隐身等[1]。声学超材料通过布拉格散射和局域共振的原理,使得小尺寸控制大波长(结构胞元尺寸小于声波波长)成为可能。2000年Liu等[2]利用硅胶包裹铅块嵌入环氧树脂体中首先制造出声学超材料。Yang等[3]利用成对的薄膜结构制造了一种具有双负特性的声学超材料,实现了宽频双负特性。Tian等[4]建立了圆形薄膜-环形质量的局域共振型声学超材料的理论模型,提出一种解析方法以研究结构的隔声量。张佳龙等[5]采用环形局域共振膜结构模型进行减振降噪设计,对带隙宽度影响因素及隔声特性进行分析。贺子厚等[6]针对低频噪声的隔离问题,设计了一种基于压电材料的可调控薄膜声学超材料,从理论上探究了结构参数对薄膜声学超材料隔声性能的影响。张炜权等[7]研究了膜内张力对其声学特性的影响。蔡梦娜等[8]对非对称结构双层薄膜局域共振声子晶体材料的声学低频隔声性能进行研究,讨论声子晶体非对称结构中质量块分布方式、位置以及数目对声学衰减特性的影响。薄膜声学超材料实现了小尺寸控制大波长,但是在隔声降噪领域,低频声波依然难以控制,隔声量与范围依然很小。由于薄膜声学超材料的研究起步比较晚,理论还不够完善,设计和应用上也还存在一些缺陷,因此还需要进一步研究、探索。
本文以薄膜声学超材料(由张紧的柔性薄膜和质量块构成)为研究对象,对其隔声机理进行分析。通过仿真分析研究不同结构参数对薄膜声学超材料隔声性能的影响,并对仿真结果进行实验验证。
1 薄膜声学超材料理论分析
对于圆形薄膜振动,极坐标下膜振动方程可表示为:
(1)

(2)
使用分离变量法求解二阶偏微分方程,最后归结为求解零阶柱贝塞尔函数根值,可求得周界固定圆形膜的频率方程。fn称为简正频率,设kna=μn,可得:
(3)
式中:kn为波数;a为薄膜半径;T为薄膜张力;ρ为单位面积膜质量。
第一阶固有频率f1为:
(4)
圆膜做自由振动时存在一系列简正频率,这些简正频率对应的简正振动方程为:
(5)
式中:j为虚数单位;ω为角频率;ηn为薄膜的横向位移;J0为零阶柱贝塞尔函数;An为系数。
取其实部为:
(6)
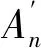
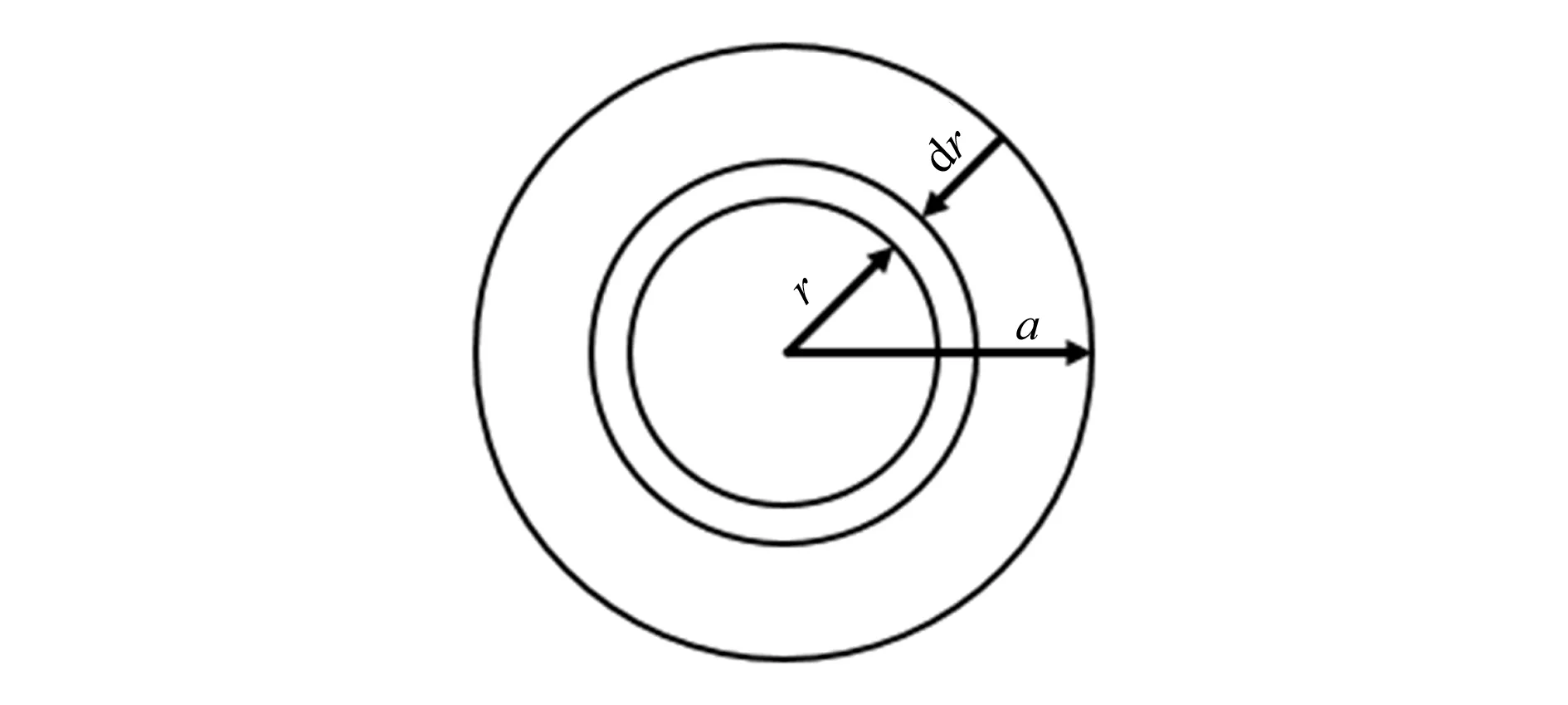
图1 圆膜面元示意图
在圆膜上取径向距离为(r,r+dr)的一个面元,该单位面元第n次振动的振动动能dEkn为:
(7)
(8)
式中:D为一个振动周期。
将式(6)代入式(8)可得:
(9)

(10)
根据贝塞尔函数关系得:
(11)
式中:J1为一阶柱贝塞尔函数。
将圆膜振动等效成一个质量-弹簧系统,等效质量Men位于圆心处,等效质量在弹簧Ken的作用下振动。在r=0处的振动位移根据式(6)可知:
(12)
振速vn为:
(13)
于是,等效平均动能为:
(14)
令式(11)与式(14)相等得到圆膜的等效质量Men:
(15)
式中:m=πa2ρ,为膜的实际质量。
第1,2次振动方式对应的等效质量Me1,Me2为:
(16)
(17)
根据圆膜的等效质量Men,通过集中参数系统的固有频率f0:
(18)
式中:Km为弹性系数;Mm为集中质量。
可以推出等效的弹性系数Ken为:
(19)
当在圆膜中心附加一集中质量Mm随圆膜一起振动时,对于一阶振动,因为圆心处等效质量为Me1,故而等效总质量为(Me1+Mm),已知一阶弹性系数Ke1,利用集中参数系统的固有频率关系可得一阶固有频率f1:
(20)
于是不难解释薄膜-质量块结构可以降低隔声频率的原因,因为中心质量的增大,使得结构固有频率降低。对薄膜声学超材料的研究通常以降低固有频率为目的,以降低低频处隔声峰频率,在峰值频段达到低频隔声效果,但对于第一阶固有频率和低于第一阶固有频率的声波,如对人体影响较为明显的频率主要为 3~50 Hz 频率范围的声波没有隔声效果。由周界固定圆形膜的频率方程式(3)可知,固有频率与薄膜半径成反比,与薄膜张力的平方根成正比。下面将对这些参数对隔声的影响进行研究。
2 仿真分析
本文对由薄膜和质量块构建的薄膜声学超材料进行隔声仿真分析。仿真软件为COMSOL Multiphysics 5.3a。物理场采用压力声学模块与固体力学耦合模块,对薄膜质量块结构进行三维建模,如图2所示,建模过程如下:1)选择物理场计算模块为压力声学与固体力学耦合模块;2)建立圆形薄膜,薄膜中央附加圆柱形质量块,建立圆柱状空气域,空气域圆柱半径与薄膜相同,空气域在薄膜两侧对称;3)设置薄膜与质量块为固体,空气域为气体,并赋予各部段材料属性;4)采用映射法划分网格;5)设置圆形薄膜周界固定条件和薄膜预应力大小。
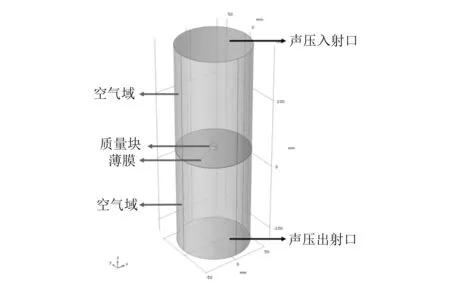
图2 薄膜质量块结构示意图
采用平面波入射法计算隔声损失,设置柱状空气域上表面为声压入射口、下表面为声压出射口,设置入射声压为单位声压1 Pa。设置变量,对入射口、出射口分别进行积分,计算声波入射口与出射口声功率,得到模型隔声损失结果。
2.1 薄膜大小对隔声损失的影响
薄膜附加质量块结构模型如图2所示,取薄膜半径分别为50,40,30,20,10 mm,薄膜厚度为0.1 mm,质量块半径与厚度均为5 mm,薄膜初始平面预应力为5 MPa,材料参数见表1。采用声固耦合研究模块,保持周界固定条件,计算得其隔声损失曲线如图3所示。

表1 薄膜声学超材料结构材料参数
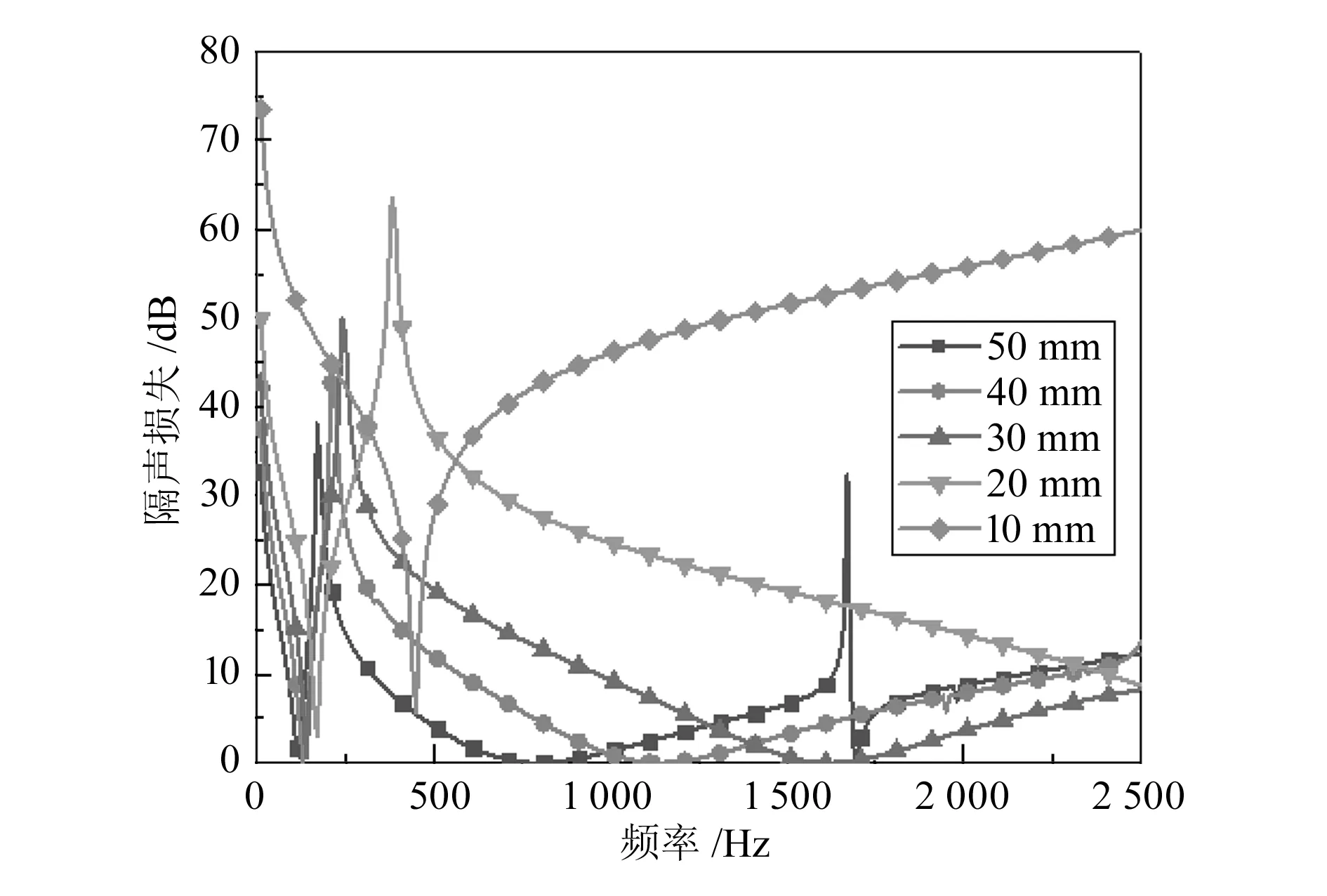
图3 圆形薄膜半径对隔声损失的影响
由图可知,在10~2 500 Hz研究频率范围内,隔声量随频率的增大先减小到第一阶固有频率处,然后逐渐增大到峰值频率处,再逐渐降低。当改变薄膜半径大小时,初始低频隔声量随着薄膜半径的减小而增大,第一隔声谷值对应频率逐渐增大,与周界固定圆形膜方程规律一致。当薄膜半径为50 mm时,初始低频10 Hz处隔声量为32.72 dB,隔声峰值170 Hz处隔声量为38.06 dB,隔声谷值120 Hz处隔声量为0.71 dB;当薄膜半径为20 mm时,初始低频隔声量10 Hz处隔声量为49.91 dB,隔声峰值380 Hz处隔声量为63.56 Hz,隔声谷值170 Hz处为3.07 dB。因此,增大第一阶固有频率,提高初始低频隔声量,同样可以提升低频隔声效果,增大低频隔声范围,且可以实现极低频处的隔声。与提高第一阶固有频率的隔声方法组合使用,可以实现低频全段声波的有效隔绝。通过对薄膜尺寸大小的调节,可以实现对不同频段声波的有效隔绝。
当薄膜半径降低到10 mm时,显示出普遍大于20 dB的隔声效果(在10~2 500 Hz计算范围内,10~420 Hz,470~2 500 Hz的隔声量大于20 dB)。隔声频率宽度与隔声效果均显著提升,显示出了明显的尺度效应。因此,薄膜尺寸越小,隔声效果越好,隔声量越大,隔声范围越广。
2.2 薄膜预应力对隔声损失的影响
取薄膜半径为50 mm,薄膜厚度为0.1 mm,质量块半径与厚度均为5 mm。材料参数见表1。薄膜面内拉伸预应力分别设置为3,5和7 MPa。采用声固耦合研究模块,保持周界固定条件,计算得其隔声损失曲线如图4所示。
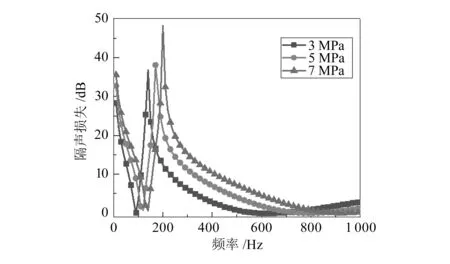
图4 预应力对隔声损失的影响
结果显示,随着薄膜预应力的增加,第一阶隔声谷值对应的频率(对应第一阶固有频率)增大,与周界固定圆形膜方程规律一致。改变薄膜预应力,同样可以改变第一阶固有频率的大小,通过调节薄膜预应力大小,可以实现不同频段声波的有效隔绝。
3 实验验证
实验所选用的仪器为B&K 4206-T声阻抗管,该测试系统主要包括计算机(测试软件)、传声器、阻抗管、音频放大器、PULSE多分析仪、声压校准器等,如图5所示。本系统阻抗管可以测量直径为100 mm的圆柱形试件,测试频率范围为50~1 600 Hz。
为进行薄膜面内拉伸预应力实验验证,制作了3种不同预应力实验试件A、B、C,预应力大小分别为4.32,7.15,7.21 MPa。试件薄膜半径为45 mm,铝边框外径为100 mm,内径为90 mm,附加质量块质量为1.06 g。材料参数见表1。仿真与实验结果如图6所示,随着面内拉伸预应力增大,峰值和谷值对应的频率增大,隔声曲线向右移动,最大隔声量的幅值变大,频带宽增大。仿真结果与实验结果拟合良好,验证了仿真方法的正确性。

图5 B&K声学测试系统4206-T部分仪器
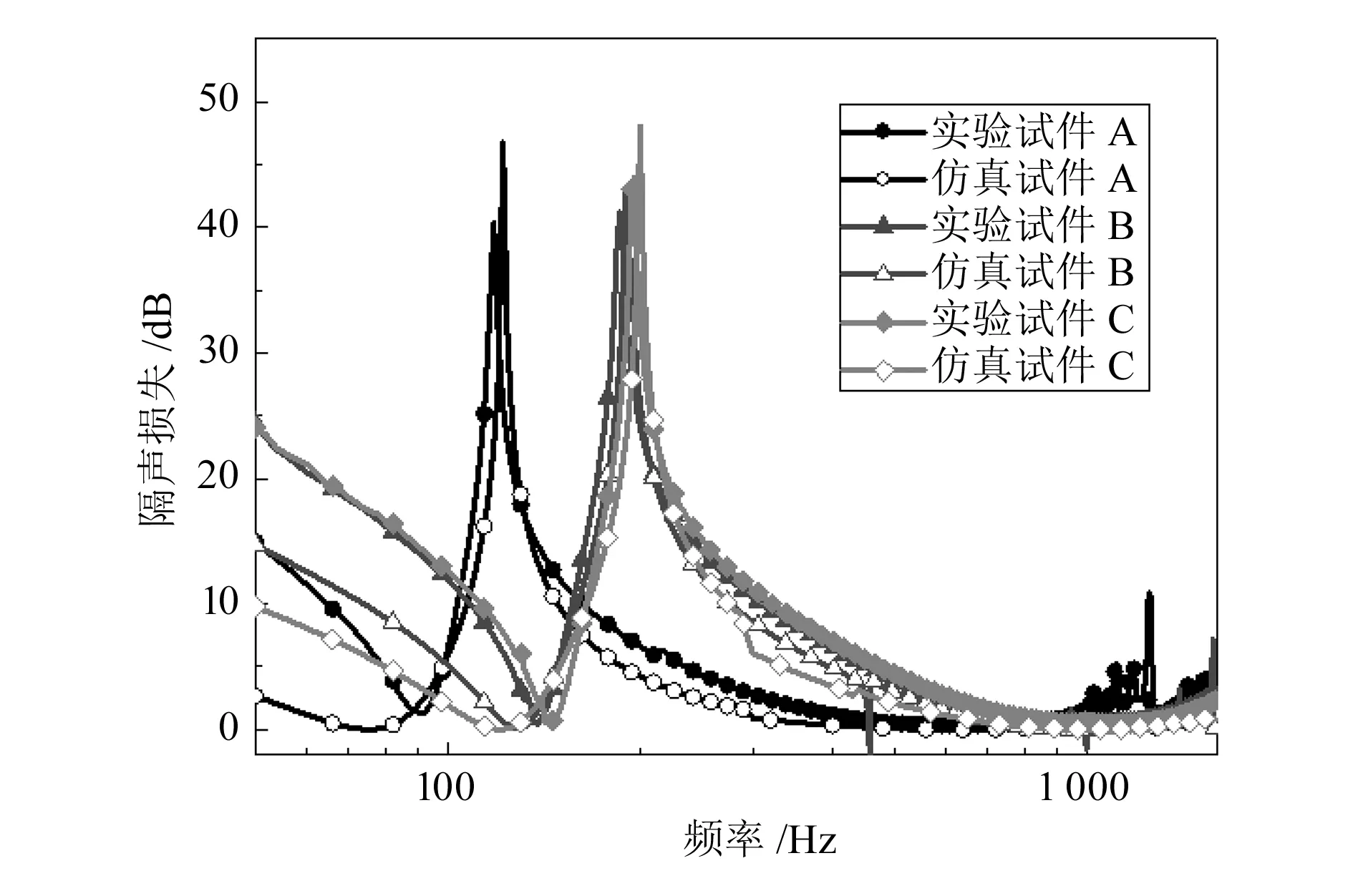
图6 面内拉伸预应力仿真与实验结果
4 结束语
本文对薄膜声学超材料隔声机理进行分析,对薄膜声学超材料进行隔声仿真与实验验证。从圆形薄膜振动方程入手,推导出周界固定圆形薄膜频率方程,分析固有频率的影响因素为半径、预应力与单位面积质量,并对薄膜质量块模型进行分析,解释了薄膜声学超材料低频隔声的原理,即通过附加中心质量降低固有频率,利用低频隔声峰对低频噪声进行隔绝。对固有频率的影响因素进行隔声损失仿真分析,研究了薄膜大小、面内拉伸预应力对薄膜型声学超材料隔声性能的影响。仿真结果表明,初始低频隔声量与第一阶固有频率随薄膜半径的减小而增大,随面内拉伸预应力增大而增大。研究发现,增大固有频率、利用隔声曲线初始低频隔声段可以对极低频声波进行有效隔绝,与降低固有频率、利用隔声曲线第一阶隔声峰值段隔声相比,隔声频率更低。这两种隔声方法组合使用,具有叠加效果,为低频隔声提供了新思路。薄膜声学超材料具有明显的尺度效应,小尺寸薄膜声学超材料可实现宽频低频隔声。最后进行了薄膜预应力大小对隔声损失影响的实验,证明了仿真方法的准确性。
