培养数学建模思想 增强数学关键能力

>>>董纪华

新高考承载着促进立德树人、考查学生关键能力和学科核心素养、助力人才选拔与培养等多重功能。纵观近几年高考数学试题，已经从只对数学知识进行考查，转向对数学能力、数学素养的考查。“数学建模”作为新课标提出的六大核心素养之一，成为近几年高考的考查热点，我们有必要从课程标准出发研究高考试题，提升关键能力。

一、从新课标看数学建模

数学建模就是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养。《普通高中数学课程标准(2017年版)》提出了六个数学学科核心素养，即数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析;设置了函数、几何与代数、统计与概率、数学建模活动与数学探究活动四条主线;提出了“三会”，即“会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界”，其中，用数学语言表达世界，就是运用数学知识、数学方法构建数学模型，解决客观世界中现实问题的能力素养。可见，在学习的过程中，我们除了要重视“四基”“四能”，也要重视数学与客观世界的联系，通过数学建模活动获得数学建模思想，活学活用数学知识，培养数学核心素养。

二、从高考评价看数学建模

《中国高考评价体系说明》指出，高考评价应基于学科核心素养确定考查的关键能力与必备知识。近年来，高考评价越来越注重数学的应用性，高考试题通过设置真实问题情境，创设开放性、可探究的问题，考查考生的数学能力。数学建模作为数学内容的主线，不仅要求同学们掌握扎实的数学知识，更要求同学们增强知识间的联系。有逻辑地运用数学知识技能解决实际问题，成为近年高考考查的趋势。高考试题将数学建模活动与数学探究活动融入考查之中，同学们虽然不能在考场上真正进行数学建模活动，但可以应用数学建模思想解决问题，将实际问题抽象为数学问题，灵活运用已有的数学知识构建数学模型，用数学的方式解决实际问题。

三、例析高考中的数学建模与数学模型

例1.(2020年全国卷Ⅲ,理科4题)Logistic模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位：天)的Logistic模型其中K为最大确诊病例数.当I(t★)=0.95K时,标志着已初步遏制疫情,则 t★约为(ln19≈3)

A.60 B.63 C.66 D.69

模型分析：本题以新冠肺炎为实际背景，引入Logistic模型揭示某地区新冠肺炎累计确诊病例数随天数的变化规律，充分体现了函数是刻画变量间变化规律的数学模型。同学们应深入理解指数型函数模型蕴含的规律特征，利用已有的函数知识，结合函数与方程的基本思想，通过对数学问题的计算，预测疫情得以遏制的规律，解决实际问题，感悟函数的预测功能。

例2.(2020年全国卷Ⅲ,理科18题)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位：天)：

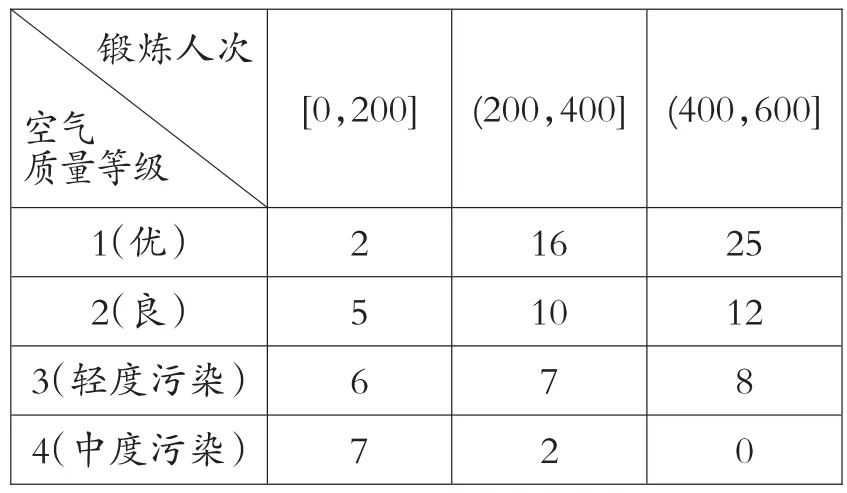
锻炼人次空气质量等级［0,200］ (200,400］ (400,600］1(优) 2 16 25 2(良) 5 10 12 3(轻度污染) 6 7 8 4(中度污染) 7 2 0

(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;

(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);

(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?

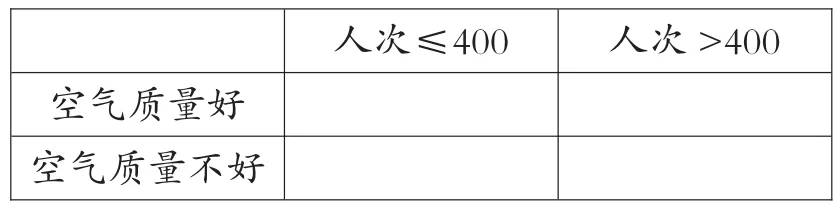
人次≤400 人次＞400空气质量好空气质量不好

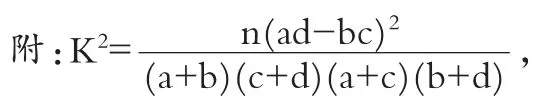
P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828

解析：(1)由频数分布表可知,该市一天的空气质量等级为1的概率为=0.43,等级为2的概率为=0.27,等级为 3的概率为=0.21,等级为4的概率为=0.09.

(2)由频数分布表可知,一天中到该公园锻炼的人次平均数为=350.

(3)2×2列联表如下：

人次≤400 人次＞400空气质量不好 33 37空气质量好 22 8

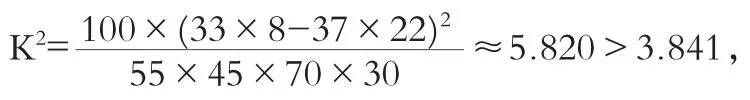
因此，有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关。

模型分析：本题以空气质量问题和公园锻炼人数的联系为背景，考查了概率统计模型。在历年高考试题中，概率统计问题通常都十分注重生产生活实际与数学知识方法的联系。现实世界中存在着很多随机现象，不确定性中又蕴含了一定的规律。我们须从大量的统计数据中分析、识别这些规律.高考试题对概率统计模型的考查，需要考生从大量文字和数据中提取关键信息，选择恰当的统计图表(如列联表、频率统计表、直方图、折线图等)整理数据，并确定关键的数字特征，反映总体特征，有时还需要检验模型并改进模型。同学们应该在复习中深入理解统计基本思想、熟练掌握统计基本模型，运用统计学基本方法获取、分析、整理数据，选择或建立恰当的概率统计模型，通过计算解决实际问题。

四、提高数学建模素养的一些建议

1.夯实基础，掌握数学模型

在构建数学模型时，我们需要对已学数学知识的本质特征有较为深刻的认识，理解与掌握数学模型的本质。如函数是刻画变量间变化规律的数学模型，概率是研究随机现象的数学模型，统计模型和统计工具往往可以帮助我们理解和处理数据，并与概率相联系研究不确定现象等，这样才能将错综复杂的现实问题与数学模型建立联系。在求解数学模型时，我们须用数学的方法和基本思想，进行逻辑推理与准确计算，如对函数性质的讨论、对方程的求解、应用数列的性质解决问题等。在检验和改进数学模型时，往往需要我们对数学解释有足够的认识，如用概率统计学知识进行风险决策，对人们的生产生活给出指导。如果模型与现实问题产生了较大的误差，我们需要根据数学专业知识检验所得结果的科学性，并改进模型。这些都需要我们夯实基础，理解每一个数学概念的本质，弄清楚定理的来龙去脉，提高数学运算能力。

2.关注知识的联系性与整体性

从高考试题的角度来看，我们会发现与数学建模思想有关的试题，考查的知识点往往并不固定，有时问题涉及的知识内容也不是单一的，综合性较强。另外，从数学学习的角度来看，我们要弄清楚构成某一个数学研究对象的要素之间的关系，以及不同研究对象之间的关系。数学知识之间总是以数学的逻辑有机、连贯地联系在一起，我们只有将数学看成一个整体，复习时注重知识间的联系，如等式与不等式的关系、函数与方程的关系、几何与代数的关系、结构与形式的关系等等，才能在综合性较强的数学建模问题中提出问题、分析问题、解决问题。

3.重视对问题背景的分析

近几年高考中与数学建模相关的题目，都以真实情境为背景，具有科学性、时效性、广泛性的特点，题目情境多种多样。例如在2020年高考中，许多地方的高考试题都加入了以“新冠肺炎”为背景的问题，也有空气质量、信息熵等实际背景。这些试题往往有大量的文字描述，还会有一些科学性、时效性较强的术语，同学们在复习中应注意对该类问题的训练，通过对材料的阅读、分析，感受问题的本质，体验从现实问题中抽象出数学问题的思维，与此同时，加深对数学知识的理解与应用。