交通道路网中时间感知的空间关键词查询
2021-04-16游青华李艳红黄金亮卢航罗昌银
游青华,李艳红*,黄金亮,卢航,罗昌银
(1中南民族大学 计算机科学学院,武汉 430074;2 华中师范大学 计算机学院,武汉 430079)
随着移动网络和地理定位技术的迅速发展,基于位置的服务被广泛地运用于日常生活中,拥有位置-文本信息的网络数据对象的数据量也随之呈爆发式增长,因此空间关键词查询的研究引起了研究者及工业界的广泛关注.空间关键词查询以一个地理位置和若干个关键词作为输入参数,以若干个空间相似度和文本相似度最高的数据对象作为结果返回.但仅考虑空间相似度和文本相似度的空间关键词查询有时无法满足用户的特殊需求,例如,对于一名在某个陌生城市旅游的游客,他会根据一些公共场所的开放时间来安排自己的旅程.如果只根据空间相似度和文本相似度来查询景点,查询的结果就不能帮助该游客做出合理的旅游安排.为了解决这类需求,可以在空间关键词查询中考虑时间信息.为了更符合实际的应用场景,本文考虑在路网下对这一问题进行研究,搜索路网中与用户提出的查询要求最为相似的k个对象.为了解决该问题,本文提出了一种能够同时使用时间、空间和文本信息对搜索空间进行剪枝的策略来削减搜索空间的规模.同时基于这种剪枝策略,本文提出了一种新的索引结构----TK,用于索引道路网中的数据对象信息.在TK索引下,本文设计了相应的查询算法来处理路网中时间感知的空间关键词查询.
1 相关工作
目前,许多文献对空间关键词查询进行了研究,例如文献[1-3].然而,这些文献里空间关键词查询中仅考虑数据对象的空间、文本维度,忽略了数据对象中包含的时间属性,而时间信息在空间关键词查询搜索中也起着十分重要的作用.近几年,关于基于时间的空间关键词查询的研究也不断涌现,例如,文献[4]中研究的是基于时间的空间关键词发布订阅的问题,其中,CHEN等人提出了条件影响域(CIR)的概念来表示时间感知的空间关键词订阅查询(TaSk),同时利用CIR设计过滤条件将多个TaSK查询进行分组处理,从而提高查询的速度.但该文献中处理时间的模型是针对时间戳类型的,无法处理时间区间这种形式.文献[5]研究了时间感知的空间关键词覆盖查询处理问题,并提出了TR-tree索引结构和有效的剪枝策略来快速地处理该类查询,但这篇文献是在欧式空间下研究的,无法解决复杂路网中时间感知的空间关键词查询问题.文献[6-7]研究了路网中基于时间的空间关键词查询问题,并提出TG索引结构来索引路网中的信息.然而这种索引在索引路网信息时存在冗余,且在查询处理过程中需要对整个搜索空间进行查找,影响了查询处理的效率.因此,本文设计了一种新的索引结构----TK来解决存储冗余,并基于该索引结构设计相应的算法提前结束查询处理,以避免对整个搜索空间的探寻.
2 问题定义
表1列出的是本文中出现的符号及其定义.

表1 符号与定义
2.1 兴趣点
假设路网G的边e∈E有一组时空文本对象o∈O,每一个对象o具有3个属性:o.loc,o.doc,o.t,其中o.loc表示对象o的位置,对象o到它所在边(vi,vj)的两端点之间的网络距离可以分别表示为|vi,o|和|o,vj|,而对象oi与oj之间的路网距离是通过路网上oi与oj之间最短路径的长度来表示的.o.doc是一组用来描述对象o的关键词集合(例如,sunshine store),o.doc的形式化定义为o.doc={(o.key1,f1),(o.key2,f2),…,(o.keyn,fn)},其中fi是o.keyi在对象o的描述中出现的频率.o.t表示对象o的有效时间(例如,Sunshine store 的开放时间为9∶00~19∶00),可以形式化定义为o.t=(o.st,o.et),路网对象的信息如表2所示.

表2 路网中对象信息
2.2 时间感知的空间关键词查询

定义2综合评分函数rank(q,o).对于查询q和对象o,评分函数rank(q,o)计算并返回综合考虑o相对q的位置邻近度、文本相似度和时间重叠率的评分,具体如下:
rank(q,o)=α·Tsim(o.doc,q.doc)+β·Dsim(o.loc,q.loc)+(1-α-β)·Tolap(o.t,q.t),
(1)
其中,Tsim(o.doc,q.doc)是o和q之间的文本相似度,Dsim(o.loc,q.loc)是o与q之间的位置邻近度,Tolap(o.t,q.t)是查询时间与对象o的有效时间的重叠率.α,β∈(0,1)表示用户的偏好参数,用于调整文本相似度、位置邻近度和时间重叠率在评分函数中的权重.
定义3文本相似度.对象o∈O与查询q之间的文本相似度可以通过一个文本相似性度量函数来计算,本文是采用cosine相似性[9]来计算q.doc和o.doc之间的文本相似度,其定义如下:
Tsim(o.doc,q.doc)=
(2)

定义4位置邻近度.位置邻近度描述的是查询q到对象o∈O之间路网距离的邻近度,其定义如下:
(3)
其中,ds(q.loc,o.loc)为查询q.loc与o.loc之间的最短网络距离,dmax表示路网中任意两点之间的最大网络距离.
定义5时间重叠率.时间重叠率是通过查询时间与路网中对象的有效时间的交集来计算的,其定义如下:
Tolap(o.t,q.t)=
(4)
其中,o.st表示o的有效时间的起始时间;q.et表示查询时间的结束时间;tw表示用户可以忍受的等待时间.如第一种情况所示,当查询q的查询时间q.t与o.t之间存在交集,即|q.t∩o.t|≠0时,对象o与查询q之间的时间相关性为正相关;如第二种情况所示,当查询的结束时间大于对象o的起始时间,且对象的起始时间与查询的结束时间的时间差值小于用户可以忍受的等待时间,即|o.st-q.et|≤tw时,对象o与查询q之间的时间相关性为负相关;其他情况,即当o.et
3 路网中TK索引结构
3.1 路网的划分
为了使提出的查询处理方法具有更好的扩展性,采用kd-tree方法[12]自适应地划分路网.通过水平方向和垂直方向将路网划分成若干个单元格,使得每个单元格中数据对象的数量大致相等.路网的划分如图1所示,这里采用的是竖直方向优先的划分方式.首先,令垂直线x=x1将路网划分成两部分,使得左边子网中包含的点有{o1,o2,o3},右边子网包含的点有{o4,o5,o6,o7}.接着,令水平直线y=y1将左边子网划分成两部分,使得每部分中数据点的数量大致相等,再对右边子网进行相同的操作.重复上述划分步骤,直到每一个子网中包含的数据点的数量不超过预设的阈值λ.在划分过程中设置λ=1.划分结束后,使用标识符R1,R2,R3,…,R7对每个子网进行标识.

图1 基于kd-tree方式划分路网
3.2 距离矩阵
TK索引结构采用的距离矩阵是一个n×n的二维矩阵Dn×n,其中n是路网中划分后的区域总数,Dn×n中的每一项存储的是区域Ri与其他任何区间之间的最小网络距离dNmin(Ri,Rj)和最大网络距离dNmax(Ri,Rj).为了得到二维矩阵Dn×n,需要先求出不同区域的所有边结点对之间的最短路径距离和每个区域中两个结点之间的最长路径长度.路径长度的计算可以采用单源最短路径算法来计算,例如Dijsktra算法[13].计算dNmin(Ri,Rj)时,从kd-tree区域Ri中的一个边顶点开始,扩展到其他区域Rj中的边结点,并选择两个区域中最邻近的两个边顶点之间的距离值作为dNmin(Ri,Rj).在计算dNmax(Ri,Rj)时,首先计算出每个区域Ri(Rj)中结点之间的最大距离即Ri的区域直径,则dNmin(Ri,Rj)、节点Ri的区域直径以及节点Rj区域直径之和是dNmax(Ri,Rj).
3.3 TK索引
路网划分结束后,以自底而上的方式构建TK索引.TK索引包含两个部分:(1)改进的kd-tree,其叶子节点可以表示为(Ri,L(Ri),IU(Ri),TU(Ri),Pd(Ri)),其中Ri是区域的标识符;L(Ri)是区域Ri中所有对象的标识符的集合;IU(Ri)是区域Ri中对象的文本信息的交集和并集,TU(Ri)是L(Ri)中所有对象的有效时间的并集,是一组时间区间集合;Pd(Ri)是区域Ri指向距离矩阵中对应的子项的指针.其非叶子节点可以表示为((xi||yi),IU(xi||yi),TU(xi||yi),Pc(xi||yi)),其中xi或者yi是划分平面,IU(xi||yi)是xi或者yi划分区域中所有对象的文本信息的交集和并集,TU(xi||yi)是xi或者yi划分区域中所有对象的有效时间的并集,Pc(xi||yi)是xi或者yi划分的区域中指向(划分后)子区域的指针;(2)距离矩阵,存储了各个区域之间的最小网络距离和最大网络距离.图2是根据图1中路网构建的TK索引结构图,表3是IU(*)中文本信息的交集和并集的集合信息表,每一项(II(ki),UI(ki))表示划分区域的文本信息的交集和并集,其中II(ki),UI(ki)分别表示某个区域中关键词ki的交集和并集.
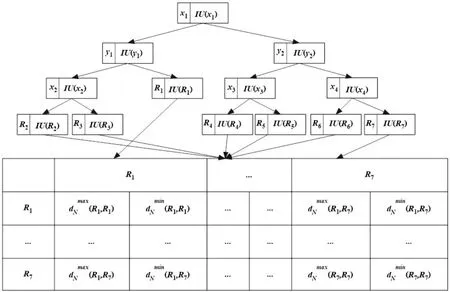
图2 TK索引结构

表3 TK非叶子节点文本信息交并集合
3.4 基于TK索引的查询搜索

引理2已知一个TSKQ查询q=(q.loc,q.doc,
q.t,q.k)和一个区域Ri,如果|q.t∩Ri.t|=0且|Ri.st-q.et|>tw时,则区域Ri可以被安全地削减.
引理3已知TSQK查询q=(q.loc,q.doc,q.t,q.k)和区域Ri,如果rankmax(Ri,q)
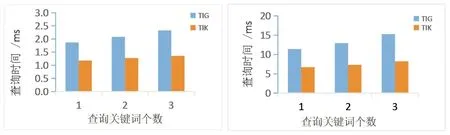
引理4已知TSQK查询q=(q.loc,q.doc,q.t,q.k)和有序候选对象集合Ocand,假设rankmax(oi,q) 算法1给出了路网下时间感知的空间关键词查询处理过程.其中,集合Ocand用于存放满足筛选条件的候选对象,集合LR用于存储整个路网的各区域.rank(ok-th,q)是结果集中第k个对象的评分,先将其初始化为-∞.该算法分如下两个阶段来实现. 输入:路网下图G中关于数据集O的TK-tree,TSKQ查询q=(q.loc,q.doc,q.t,q.k)输出:q的查询结果集合Sr//阶段1:对整个搜索空间使用筛选条件进行过滤,得到候选区域及候选对象1 Ocand=⌀;rank(ok-th,q)=-∞;Sr=⌀;LR=⌀;2 定位到查询q所在的区域Rq,并将除Rq以外的其他区域Ri(1≤i≤n)根据dNmin(Ri,Rq)从小到大排列在有序列表LR中;3 foreachobjecto∈Rqdo4 ifrank(o,q)>rank(ok-th,q)then5 根据rank(o,q)将对象o(o,rank(o,q))从大到小插入到Ocand;6 rank(ok-th,q)←Ocand中评分最小的第k个对象的rank(ok-th,q);7 foreachregionRiinLRdo8 ifrank(Ri,q)=-∞then9 continue;10 ifrankmax(Ri,q)=1-βdsmin(Ri,Rq)dmax 下文以基于TG索引结构的算法TIG作为对照算法,通过一系列对比实验来验证本文提出的基于TK索引的TIK算法的性能. 实验采用了两个合成的数据集CA和SF,CA是通过真实的、美国加利福利亚州的路网数据与实验系统随机产生的数据对象合成的,其中,随机产生的每个对象包含关键词信息、有效时间信息和位置信息;SF是由美国旧金山湾的真实的路网数据与实验系统随机产生的对象合成的.CA包含1458个数据对象和46个关键词,SF包含10000个数据对象和215个关键词.对于CA中的每一个对象,通过Zipf分布[14]为其分配2-4个关键词,每个对象的有效时间范围设置在[1-24],且遵循高斯分布[15];对于SF中的每一个对象同样采用Zipf分布的方式为其设置3个关键词,SF与CA中对象的时间信息的设置方式相同.注意,每个对象的位置都随机地分布在路网的边上.由于以上数据集是根据数据对象的时间特征和关键词特征进行合成的,因此对实验结果没有影响.表4描述的是两个数据集的特征,表5是实验参数的设置. 表4 实验数据集特点 表5 参数设置 实验设备为AMD Radeon,Intel Core i5-4210U,2.40 GHz CPU,8.00GB RAM Windows 10 的电脑,所有算法是在Java 1.8.0_191的运行环境下完成的. (1)k值的影响.首先研究查询返回的对象数(k值)对算法的影响.由图3可以看出,随着k值的增加,两种算法在两个数据集上的查询性能都比较稳定;总体而言,TIK算法的查询处理速度比TIG算法要快一些,这是因为TIK算法是通过时间、空间和文本信息同时对搜索空间进行削减,而TIG采用的是时间和文本信息分开的剪枝策略. (a)CA (b)SF (2)查询关键词的影响.从图4可以看出,随着查询关键词的增加,两种算法在两个数据集上的查询处理时间也随之增加.这是因为随着查询关键词个数的增多,查询的搜索空间变大,且查询待处理的对象的规模也变大.但是,从图4可以看到,TIK的查询性能仍然优于TIG. (a) CA (b) SF (3)偏好参数的影响. 1)α的影响.如图5(a)所示,在CA和SF数据集上,TIG算法查询时间会随α的增大而增大,增大幅度略大,而在CA上TIK算法代价随着α增大也会慢慢地增长,增长幅度相对于TIG要小一些; 2)β的影响.从图5(b)可以看出,两种算法查询时间是随着β增大而减小,这是因为当β增大时,位置临近度权重加大,更多离查询点远的区域或对象被削减掉.因此,β对两种算法的影响相似; (a)α 值的影响 (b)β 值的影响 3)1-α-β的影响.此处效果图(省略)类似于图3.两种算法在两个数据集上的查询性能是比较稳定的,其查询时间并不会随着1-α-β的增大而增加.总体而言,TIK算法查询性能优于TIG算法. (4)查询时间长度的影响.此处效果图(省略)类似于图3中的两幅图.在CA上,随着查询时间长度增大,TIG查询时间也在缓慢地增加,而TIK查询时间较TIG来说比较平稳.在SF上,随着时间的增长,两种算法查询时间都比较稳定,但图中TIK算法查询性能优于TIG算法. 本文研究了道路网中时间感知的空间关键词查询问题.为了便于该类查询的处理,设计了相应的索引结构——TK来组织路网中的信息.TK包括两部分:一个是改进的kd-tree,另一个是一个路网中的距离矩阵.基于TK索引结构,设计了可以同时使用文本、空间和时间信息对搜索空间进行削减的剪枝策略,并设计了相应的TIK查询处理算法.最后,采用两个真实路网的合成数据作为实验数据集,通过TIK与TIG算法的一系列对比实验,证明了所提出方法的可行性与高效性.
4 对比实验
4.1 实验设置


4.2 实验结果


5 总结
