有限域2n上一类二项式的密码学性质

王一博，夏永波

(中南民族大学 数学与统计学学院，武汉 430074)

1 基础知识

实际应用中，若Δf越小，函数的抗差分攻击能力就越强.注意到，若x是方程f(x+a)+f(x)=b的一个解，显然有x+a也是方程的解，从而该方程的解成对出现.于是f(x)可能取到最小的差分一致性为2.当Δf=2时，称f(x)为几乎完全非线性函数(almost perfect nonlinear function)，简称为APN函数[6].

Ωf={ω0,ω1,…，ωk},

另外，在文[8]中有如下等式成立：

(1)

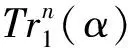
n-j.

注意到：

上式表明Qλ(x)的秩总是一个偶数2h，满足2≤2h≤n.

下面的引理给出一类特殊二次型的秩的取值范围.

为了方便后续结论的证明，给出如下定理.

上述两个函数有以下性质：

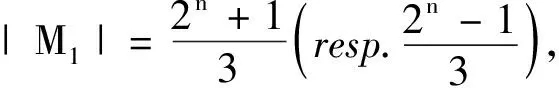
利用上述记号，下面的引理给出Ni与nj的关系,为后续的计算提供已知条件.

特别地，当n为奇数且L(F)=2(n+3)/2时，有n1≠0，同时有N2=3n3成立.

1+A1z+A2z2+…+Anzn,

并称序列(1,A1,A2,…,An)为码C的重量分布.

2 主要结果及证明

F(x)=x22t+1+x2t+1,

(2)

由以上引理，可得出F(x)的差分一致性和非线性度.

定理2令F(x)为式(2)中定义的函数，则F(x)是四差分一致的函数，其差分谱如下：

(1)当n为奇数时，ΩF={ω0=5·22n-3-3·2n-2,ω2=22n-2,ω4=22n-3-2n-2}；

(2)当n为偶数时，ΩF={ω0=5·22n-3-2n,

ω2=22n-2+2n-1,ω4=22n-3-2n-1}.

F(x+a)+F(x)+b=ax22t+ax2t+(a22t+a2t)x+F(a)+b,由于a≠0，因而F(x+a)+F(x)+b=0等价于x22t+x2t+cx+d=0,其中：

注意到c=0当且仅当a=1.下面先考虑如下线性化多项式：

x22t+x2t+cx=0.

(3)

x22t-1+x2t-1+c=0,

(4)

由于c的特殊性，x=a必然是方程(4)的解.令y=x2t-1，则上式等价转化为：

y2t+1+y+c=0.

(5)

表1 F(x)的Walsh谱

证明当a=0时，容易得出：

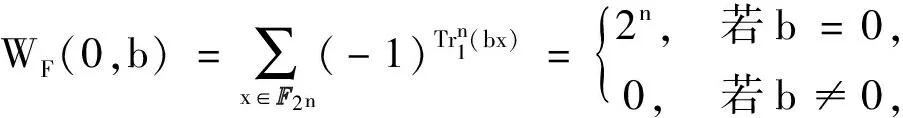
WF(a,b)=

由引理3知，2n-2-|M2|=3n3，再结合n1+n3=

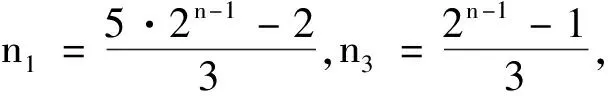
当n为偶数时，存在3个变量n0,n2,n4，然而目前只得到两个相关条件：

(1)n0+n2+n4=2n-1;

ΩF={ω0=616,ω2=256,ω4=120},

其Walsh变换的分布为：

非线性度NL(F)=8，以上数值结果分别与定理2和定理3的结论一致.

ΩF={ω0=2496,ω2=1056,ω4=480},

其Walsh变换的分布为：

非线性度NL(F)≥16，以上数值结果分别与定理2和定理3的结论一致.

注1 当n为偶数时，目前无法得出Walsh谱.倘若利用F(x)去构造线性码，码的参数未知.因而下面的应用主要是基于n为奇数的前提条件.

3 实际应用

当密码函数具有较好的密码学性质时，常可以用来构造性能优异的编码.下面利用F(x)，构造出如下两种不同的二元线性码.

定理4令F(x)为式(2)中定义的函数.设n为奇数，定义二元线性码

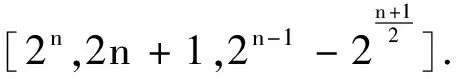
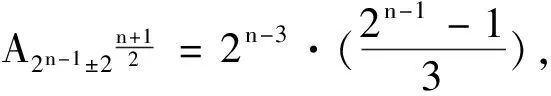
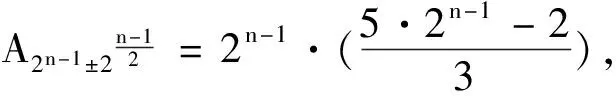
A2n-1=3·2n-2+9·22n-3-2,

A2n=1,

对其他的i，有Ai=0.

定理5令F(x)为式(2)中定义的函数.设n为奇数，定义二元线性码

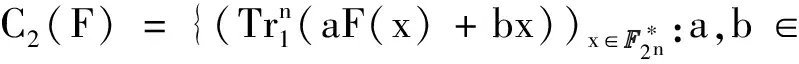
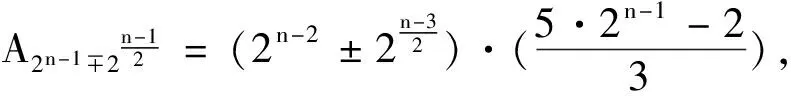
A2n-1=3·2n-3+9·22n-4-1,

对其他的i，有Ai=0.

例3 令n=5,t=3，则式(2)中的函数F(x)=x65+x9.定义二元线性码

则C1(F)的参数[32,11,8].进一步地，利用Magma软件，可得C1(F)的重量分布如下：

A24=A8=20,A20=A12=416,A16=1174,A32=1,

对其他的i，有Ai=0.以上数值结果与定理4的结论一致.

例4 令n=7,t=5，则式(2)中的函数F(x)=x1025+x33.定义二元线性码

则C2(F)的参数为[127,14,48].利用Magma软件，可得C2(F)的重量分布如下：

A48=210,A56=3816,A64=9263,

A72=2968,A80=126,

对其他的i，有Ai=0.以上数值结果与定理5的结论相符.

4 结语